奈曼皮尔逊N-P（Neyman-Pearson）定理

---

N-P定理

对于一个给定的$P_{FA}=\alpha$，使$P_D$最大的判决为
$$L(\mathbf{x})=\frac{p\left(\mathbf{x};H_1\right)}{p\left(\mathbf{x};H_0\right)}>\gamma$$
其中，门限$\gamma$由
P F A = ∫ { x : L ( x ) > γ } p ( x ; H 0 ) d x = α P_{F A}=\int_{\{\mathbf{x}: L(x)>\gamma\}} p\left(\mathbf{x} ; H_{0}\right) d \mathbf{x}=\alpha PFA​=∫{x:L(x)>γ}​p(x;H0​)dx=α
求出。

---

推导

NP定理的定义是：对于固定$P_{FA}$使$P_D$最大的判决，即
$$\text{ max }{P}_D\text{ s.t. }{P}_{FA}=\alpha$$
采用拉格朗日乘子，构造目标函数
$$\begin{array}{rl}F& =P_D+\lambda \left(P_{FA}-\alpha \right)\\ & ={\int }_{R_1}p\left(\mathbf{x};{\mathcal{H}}_1\right)d\mathbf{x}+\lambda \left({\int }_{R_1}p\left(\mathbf{x};{\mathcal{H}}_0\right)d\mathbf{x}-\alpha \right)\\ & ={\int }_{R_1}\left(p\left(\mathbf{x};{\mathcal{H}}_1\right)+\lambda p\left(\mathbf{x};{\mathcal{H}}_0\right)\right)d\mathbf{x}-\lambda \alpha \end{array}$$
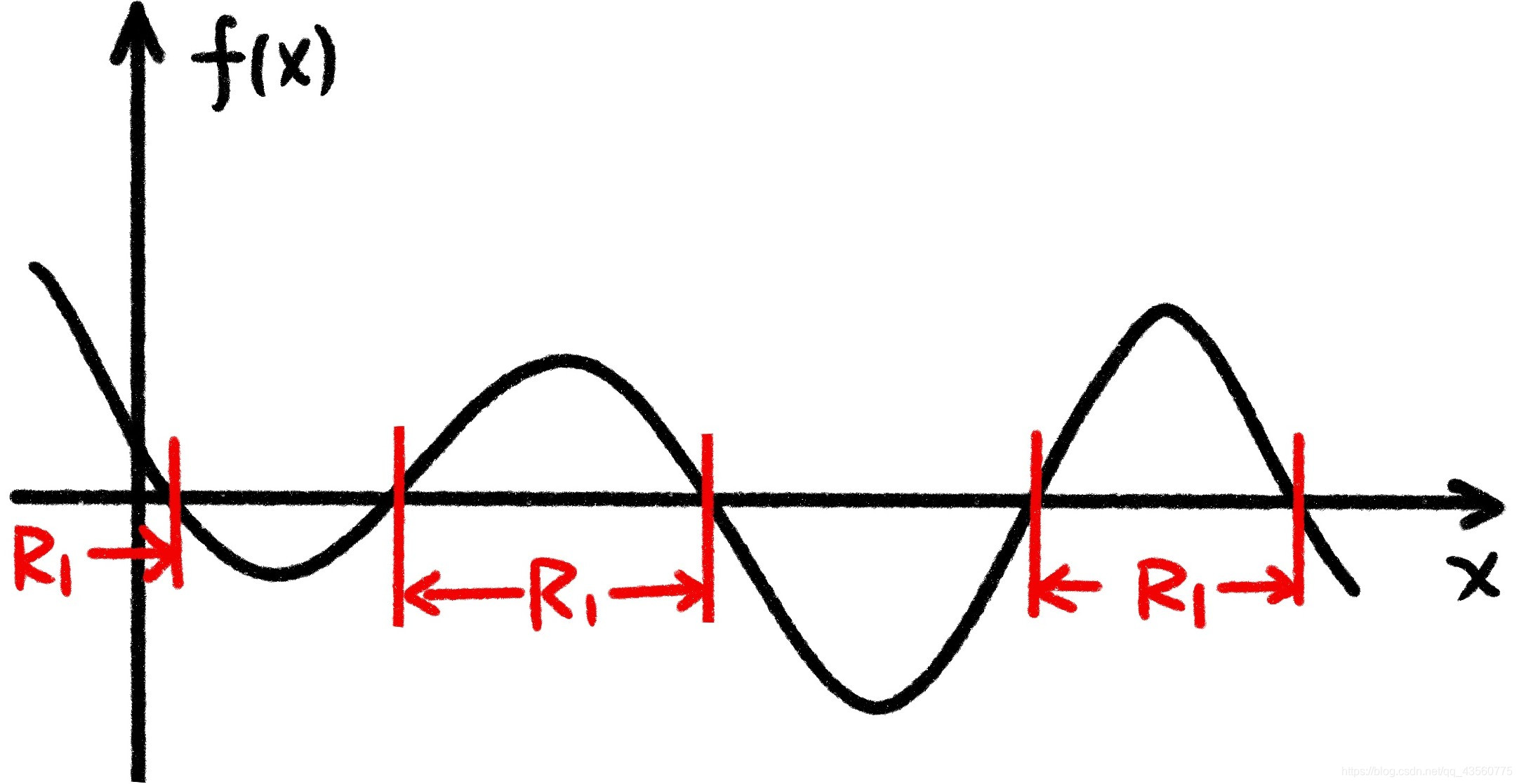
为了使目标函数F最大，应该在$x\in R1$的情况下让$f(\mathbf{x})$大于零
$$f(\mathbf{x})=p\left(\mathbf{x};{\mathcal{H}}_1\right)+\lambda p\left(\mathbf{x};{\mathcal{H}}_0\right)>0\text{ ， }\mathbf{x}\in R1$$

此时在$R1$域对$f(\mathbf{x})$的积分最大。
所以在判决时，若
$$\frac{p\left(\mathbf{x};{\mathcal{H}}_1\right)}{p\left(\mathbf{x};{\mathcal{H}}_0\right)}>-\lambda$$
判为$H_1$。
令$\gamma =-\lambda$，得到
$$\frac{p\left(\mathbf{x};{\mathcal{H}}_1\right)}{p\left(\mathbf{x};{\mathcal{H}}_0\right)}>\gamma$$
判$H_1$。其中门限$\gamma >0$由$P_{FA}=\alpha$求得
P F A = ∫ { x : L ( x ) > γ } p ( x ; H 0 ) d x = α P_{F A}=\int_{\{\mathbf{x}: L(x)>\gamma\}} p\left(\mathbf{x} ; H_{0}\right) d \mathbf{x}=\alpha PFA​=∫{x:L(x)>γ}​p(x;H0​)dx=α

参考《统计信号处理基础》