傅里叶级数和傅里叶变换

一.三角函数系

{sin 0x, cos 0x, sin x, cos x, sin 2x, cos 2x, ......, sin nx, cos nx, ......}

上面集合中不同的三角函数之间是正交的，首先可以从两个向量的内积出发，如果两个向量是正交的，那么内积等于0，而随着每一个向量的维数增加到n个，内积就是两个向量之间n个位置的相乘再相加。如果两个向量都变成了连续的函数，那内积的求和就变成了取积分，当着两函数的内积等于0就说明函数正交。

证明可以用积化和差来求积分，最后得到下面的结论：

二.周期为2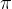的函数展开

对于2周期的函数可以展开成

三.周期为2L的函数展开

 四

 五.傅里叶变换

 

 右上是时域表达，右下显示在不同频率下系数的值，属于是频域表达，一般平时看到的不会是这种复平面的三维图，而是把复数Cn的幅度拿出来看不同频率的强度

 六.总结

首先第一部分先认识三角函数系的正交性，

其次，第二部分提出周期为2的函数可以展开成多个三角函数的加和，再利用第一部分认知的三角函数之间的正交性求得展开后的三角函数的系数

再者，第三部分就过渡到周期为2L的函数展开，直接换元就行

 

 而上述得到的式子很多很麻烦，这就用到复指数的表达形式，将上述式子进行统一，利用下面这个转换代入第三部分的式子

就可以得到周期为2L傅里叶级数的复数形式（第四部分）

再进一步，就将周期函数的周期无穷大转为非周期，就是第五部分得到终极的傅里叶变换

注意这里的w和上面第四部分的是没有关系的，这里的w是个连续的函数

当然s=iw就会变成拉普拉斯变换