动态规划DP模板题汇总

前言

动态规划的实现逻辑是画图分前后状态，二维数组肯定能解决，但是为了降低复杂度，又会转换成一维数组，线性DP，或者存在反向DP，能节省很多思考的情况。并且保证状态的更新不会影响之前状态的计算结果。

背包问题

01背包

有N件物品和容量为V的背包，每一件可以使用一次求解存放物品体积不超容量，价值最大怎么解。
斜体在题目的后面变形会作为特例讲解。

1. 状态f[i][j]定义：前 ii 个物品，背包容量 jj 下的最优解（最大价值）：

2. 当前的状态依赖于之前的状态，可以理解为从初始状态f[0][0] = 0开始决策，有 NN 件物品，则需要 NN 次决 策，每一次对第 ii 件物品的决策，状态f[i][j]不断由之前的状态更新而来。

3. 当前背包容量不够（j < v[i]），没得选，因此前 ii 个物品最优解即为前 i−1i−1 个物品最优解：对应代码：f[i][j] = f[i - 1][j]。

4. 当前背包容量够，可以选，因此需要决策选与不选第 ii 个物品：选：f[i][j] = f[i - 1][j - v[i]] + w[i]。或者不选：f[i][j] = f[i - 1][j] 。

for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }    
 // 二维变一维的原因是只求最大价值就行，每个物品考虑放不放入i不影响，因为每一个都会被检验
 //只有当枚举的背包容量 >= v[i] 时才会更新状态，因此我们可以修改循环终止条件进一步优化。同时边输入边处理。
for(int i = 1; i <= n; i++) {
        int v, w;
        cin >> v >> w;      // 边输入边处理
        for(int j = m; j >= v; j--)
            f[j] = max(f[j], f[j - v] + w);
    }     
//另一种写法都可以
for(int i = 1 ; i <=n ;i++)
    for(int j = v[i] ; j <=m ;j++)
        f[j]=max(f[j],f[j-v[i]]+w[i]);

完全背包问题

结合上面题目的变形，每种物品可以无限件的使用，
先用01背包的思路写出最简单的基础暴力模型

for(int i = 1;i <= n;i++)
        for(int j = 0;j <= m;j++)
            for(int k = 0;k <= j/v[i];k++)
                f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);

把一组商品的不同个数作为价值和体积的浮动变化，等价于多个01背包

完全背包的优化

for(int i = 1 ; i <=n ;i++)
    for(int j = 0 ; j <=m ;j++){
        f[i][j] = f[i-1][j];//放不进去的时候就保持之前的最大值状态
        if(j-v[i]>=0) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
    }

多重背包

这次是背包中物品会存在数量限制
朴素算法，也就是在背包里每一个拆，一个一个加进去，类似于完全背包，只不过有限制的k

for(int i = 1; i <= n; i ++){//枚举背包
        for(int j = 1; j <= m; j ++){//枚举体积
            for(int k = 0; k <= s[i]; k ++){
                if(j >=  k * v[i]){
                    f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }
    }

优化后的代码，将所有的s个物品拆分成新的物品，根据它的组合重量和组合价值进行标记，然后把新的组合商品看成一个物件，也就是新增商品种类之后的01背包。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000;

int f[N], v[N], w[N];
int n, m;

int main(){
    cin >> n >> m;

    //将每种物品根据物件个数进行打包
    int cnt = 0;
    for(int i = 1; i <= n; i ++){
        int a, b, s;
        cin >> a >> b >> s;

        int k = 1;
        while(k <= s){
            cnt ++;
            v[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if(s > 0){
            cnt ++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }

    }

    //多重背包转化为01背包问题，也可以用一个一个加入的二维01背包表达
    for(int i = 1; i <= cnt; i ++){
        for(int j = m; j >= v[i]; j --){
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }

    cout << f[m] << endl;

    return 0;
}

分组背包

有 N 组物品和一个容量是 V 的背包。每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大，输出最大价值。

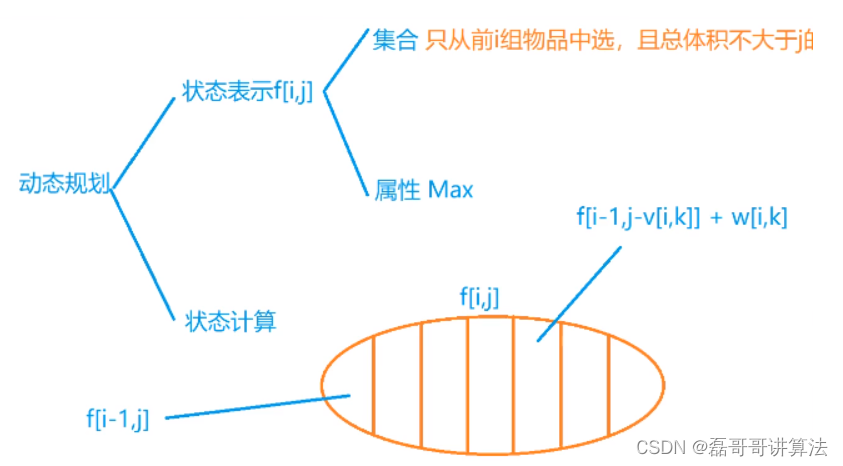
通俗的解法，也是所有01背包里面加需求而已

for(int i = 1; i <= n; ++i){
        for(int j = 1; j <= m; ++j) {
            for(int k = 0; k <= s[i]; ++k){   
            // 注意这里的k是从0开始的，就是考虑第i组不选的情况
                if(v[i][k] <= j) 
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
            }
        }   
    }

第二种解法就涉及到了解题的筛选思维，
首先将集合分为两部分
(1) 不包含第i组的部分 (2) 必须包含第i组的部分

• (1) 部分很好表示就是 f(i - 1, j) ,
• (2) 部分为上面分析的是包含第i组的第一个物品，还是第二个物品，还是第k个物品, 这样思考的话代码可以写为:

#include<iostream>
using namespace std;

constexpr int N = 110;
int n,m;
int v[N][N], w[N][N], s[N];
int f[N][N];

auto main() -> int
{
    cin >> n >> m;

    for(int i = 1; i <= n; ++i)
    {
        cin >> s[i];
        for(int j = 1; j <= s[i]; ++j)
        {
            cin >> v[i][j] >> w[i][j];
        }
    }
//是第i类里面的j是i类里的物品，k是数量，来保证了价值
    for(int i = 1; i <= n; ++i)
    {
        for(int j = 1; j <= m; ++j)
        {
            f[i][j] = f[i - 1][j];         // 这里为 f(i,j) 的第一部分
            for(int k = 1; k <= s[i]; ++k)   // 这里for的k从1开始， 为f(i,j)的第二部分
            {
                if(v[i][k] <= j) 
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
            }
        }   
    }
    cout << f[n][m] << endl;  
    return 0;
}

线性DP

数字三角形

从定点走到最后的最大路径和，每一个点有对应的方向走法，可以在理解上认为是正方形的上半部分，左下方向是行，右下方向是列的标记数组，

int a[N][N];
int f[N][N];
int main () {
    cin >> n;
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= i;j++) cin >> a[i][j];
    }
   //for (int i = 1;i <= n;i++) f[n][i] = a[n][i];
    for (int i = n ;i >= 1;i--) {
        for (int j = 1;j <= i;j++) {
            f[i][j] = max (f[i + 1][j],f[i + 1][j + 1]) + a[i][j];
            //逆着积累上去，DP来源是
        }
    }
    cout << f[1][1] << endl;
    return 0;
}

最长上升子序列

给定一个长度为N的数列，求数值严格单调递增的子序列的长度最长是多少
还是用DP中最简单的状态理解法

for (int i = 0; i < n; i++) {
        f[i] = 1;    // 设f[i]默认为1，找不到前面数字小于自己的时候就为1
        for (int j = 0; j < i; j++) {
            if (w[i] > w[j]) f[i] = max(f[i], f[j] + 1); 
            // 前一个小于自己的数结尾的最大上升子序列加上自己，即+1
        }
        mx = max(mx, f[i]);
        //雷同于怪盗基德的滑翔，也可以应用那个滑雪题目，滑雪是四个方向且st标记访问节点
    }

优化可以设想动态规划+二分法

1. 状态表示：f[i]表示长度为i的最长上升子序列，末尾最小的数字。(长度为i的最长上升子序列所有结尾中，结尾最小min的) 即长度为i的子序列末尾最小元素是什么。
2. 状态计算：对于每一个w [i] 当前末尾最小元素为w[i]。 若w[i]小于等于f[cnt-1],说明不会更新当前的长度，但之前末尾的最小元素要发生变化，找到第一个 大于或等于 (这里不能是大于) w[i]，更新以那时候末尾的最小元素。
3. f[i]一定以一个单调递增的数组，所以可以用二分法来找第一个大于或等于w[i]的数字。index提速

f[cnt++] = w[0];
    for (int i = 1; i < n; i++) {
        if (w[i] > f[cnt-1]) f[cnt++] = w[i];
        else {
            int l = 0, r = cnt - 1;
            while (l < r) {
                int mid = (l + r) >> 1;
                if (f[mid] >= w[i]) r = mid;
                else l = mid + 1;
            }
            f[r] = w[i];
        }
    }

最长公共子序列

主要是状态的考虑

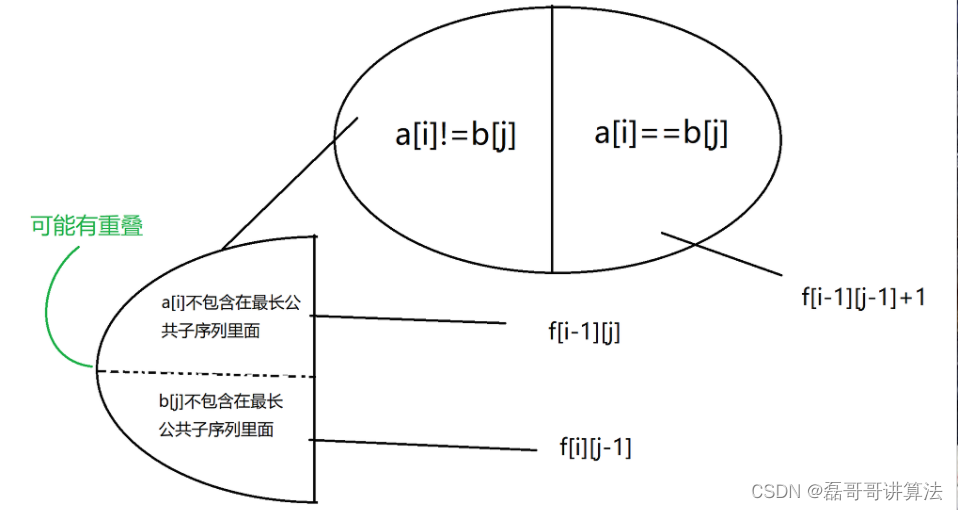
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
      if (a[i] == b[j]) {
        f[i][j] = f[i - 1][j - 1] + 1;//能相配，就都在原基础上加
      } else {
        f[i][j] = max(f[i - 1][j], f[i][j - 1]);
        //配不上的原因有误，那需要找到之前状态的最长子序列数，之前的两种状态是
      }
    }
  }

最短编辑距离

给定两个字符串A和B，现在要将A经过若干操作变为B，可进行的操作有：

删除–将字符串A中的某个字符删除。
插入–在字符串A的某个位置插入某个字符。
替换–将字符串A中的某个字符替换为另一个字符。
现在请你求出，将A变为B至少需要进行多少次操作。
情况分析
f[i][j]表示把a[1_i]变成b[1j]需要的最少操作数

本题的dp需要分析三种状态：

1，a[i]通过删除最后一个字符变成b[j]；

2，a[i]通过在最后加上一个字符变成b[j]；

3，a[i]通过把最后一个字符替换变成b[j];

第一种情况对应的方程：dp[i-1][j]+1(此时前a的i-1项和b的前j项已经相同)；

第二种情况对应的方程：dp[i][j-1]+1(此时前a的i项和b的前j-1项已经相同)；

第三种情况对应的方程：dp[i-1][j-1]+1或dp[i-1]j-1；

第一二种情况的状态转移方程dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);

第三种状态转移方程分两类a[i]与b[j]相同或不同

#include <iostream>
#include <algorithm>
using namespace std;
const int N=1005;
int n,m;
char a[N],b[N];
int dp[N][N];
int main(){
	cin>>n>>a+1>>m>>b+1;
	for(int i=0;i<=n;i++) dp[i][0]=i;//初始化（即把a从1到i变成b[0]需要i步，删除a1
	到i） 
	for(int i=0;i<=m;i++) dp[0][i]=i;//初始化（即把a从1到i增加i个字符） 
	for(int i=1;i<=n;i++){
	    for(int j=1;j<=m;j++){
	        dp[i][j]=min(dp[i-1][j]+1,dp[i][j-1]+1);
	        if(a[i]==b[j]){
	            dp[i][j]=min(dp[i][j],dp[i-1][j-1]);
	        }
	        else {
	            dp[i][j]=min(dp[i][j],dp[i-1][j-1]+1);
	        }
	    }
	}
	cout<<dp[n][m];
	return 0;
}

区间DP

石子合并

所有的区间DP问题的时候，第一维度通常是枚举区间长度，并且一般len=1是用来初始化的，从len=2开始，第二维枚举起点，右端点自动获得i+len-1；

#include<cstdio>
#include<algorithm>
using namespace std;
int a[400],f[400][400];
int s[400];//前缀和
//f[i][j]表示从i到j合并石子的最小值
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        s[i]+=a[i]+s[i-1];//区间合，从左累加到右的单位价值
    }//值的变化是谁先加，谁在移动的时候就有附加值
    for(int len=2;len<=n;len++){//先确定长度区间内进行合并
        for(int i=1;i+len-1<=n;i++) {
        /*合并区间内有左也有右，固定长度的区间要有一个暴力遍历的过程
        长度为2的合并，长度为3的合并到长度为n的合并
        */
            int l=i,r=i+len-1;//合并确定的左右侧
            f[l][r]=0x3f3f3f3f;//赋值为无穷大
            for(int j=l;j<=r;j++) {//左侧到k的最小合并 与k到右侧最小合并 +折跃的区间和
                f[l][r]=min(f[l][r],f[l][j]+f[j+1][r]+s[r]-s[l-1]);
                //s[r]-s[l-1]指的是合并的代价，也就是前缀和思想
            }
        }
        /*
        假设len=3的合并，左侧是1右侧是3，找到了k是2，那么就是以2位中间区别点
        1到2的合并+2到3的合并，区间和是1到3之间也及时s[3]-s[1]
        分而治之的情况，可以用归并排序理解一下
        */
        
    }
    printf("%d",f[1][n]);
    return 0;
}

计数DP

整数划分

这道题是很简单的线性DP，也是天大901研究生考试中的一道大题
假如将题目内容变化理解为。把1,2,3, … n分别看做n个物体的体积，这n个物体均无使用次数限制，问恰好能装满总体积为n的背包的总方案数（完全背包问题变形）

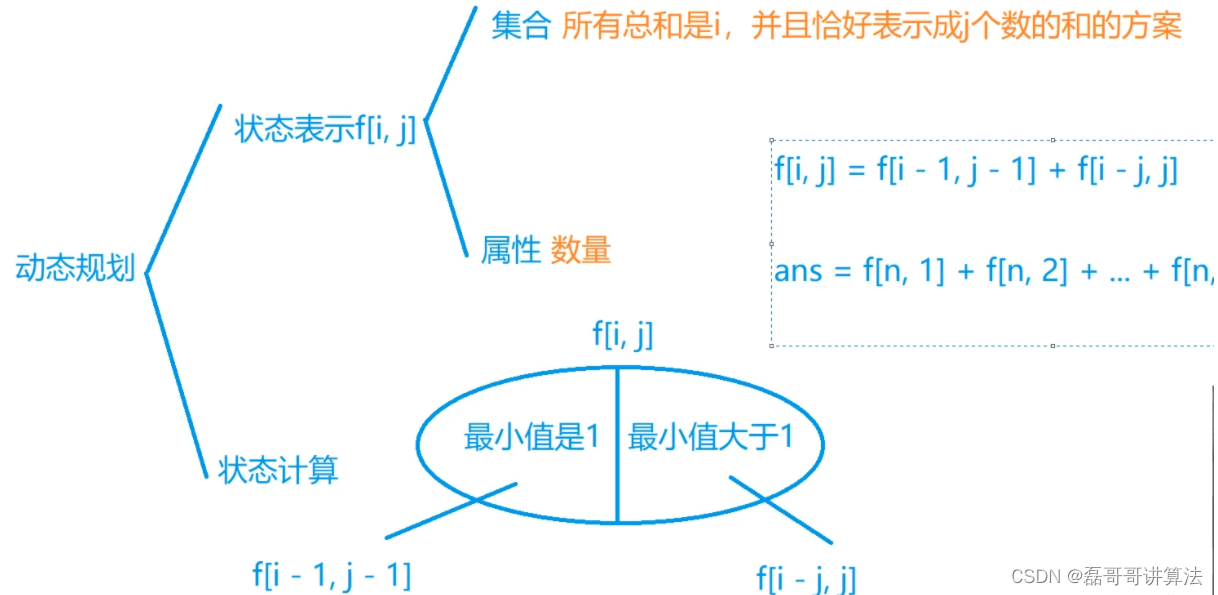
//一维
    f[0] = 1;
    for(int i = 1; i <= n; i ++)
        for(int j = i; j <= n; j ++)
            f[j] = (f[j] + f[j - i]) % M; 
    cout << f[n] << endl;
//二维 好理解，就是数字除了从1排到此数的累加，和减去一个i值后的变种加到i在变成i+x=j
for(int i = 0 ; i <= n ; i++){
        f[i][0] = 1;
    for(int i = 1 ; i <= n ; i++ ){
        for(int j = 0 ; j <= n ; j++ ){ //j >= i
            if(j >= i )
                f[i][j] = (f[i-1][j] + f[i][j-i])%mod;
            else    
                f[i][j] = f[i-1][j] ;
        }
    }

状态压缩

蒙德里安的梦想

解题思路是将横格放了之后，考虑竖格的存放方式。
总方案数等于只横放的小方块的合法方案数，剩余的位置也得保证有连续的空着的小方块，需要是偶数个

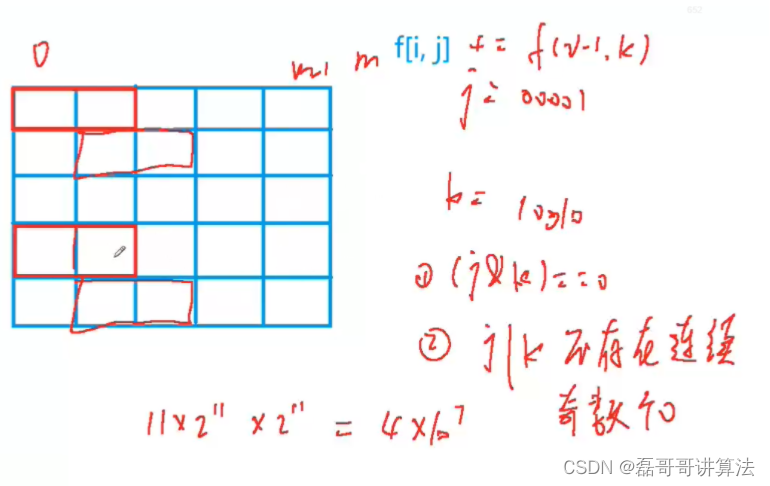
遍历每一列，i列的方案数只和i-1列有关系
j&k==0， i-2列伸到i-1的小方格 和i-1列放置的小方格 不重复。
每一列，所有连续着空着的小方格必须是偶数个
状态表示 f[i][j]: 前i-1列已经确定，且从第i-1列伸出的小方格在第i列的状态为j 的方案数。属性：个数。
i=2, j=11001 表示下列图的状态，根据格子的存放形式确定是否是1或者是0，标记i-1的计算状态用于i的新标记。

#include<iostream>
#include<cstring>

using namespace std;

//数据范围1~11
const int N = 12;
//每一列的每一个空格有两种选择，放和不放，所以是2^n
const int M = 1 << N;
//方案数比较大，所以要使用long long 类型
//f[i][j]表示 i-1列的方案数已经确定，从i-1列伸出，并且第i列的状态是j的所有方案数
long long f[N][M];
//第 i-2 列伸到 i-1 列的状态为 k ， 是否能成功转移到 第 i-1 列伸到 i 列的状态为 j
//st[j|k]=true 表示能成功转移
bool st[M];
//n行m列
int n, m;

int main() {
//    预处理st数组
    while (cin >> n >> m, n || m) {
        for (int i = 0; i < 1 << n; i++) {
//            第 i-2 列伸到 i-1 列的状态为 k ， 
//            能成功转移到 
//            第 i-1 列伸到 i 列的状态为 j
            st[i] = true;
//            记录一列中0的个数
            int cnt = 0;
            for (int j = 0; j < n; j++) {
//                通过位操作，i状态下j行是否放置方格，
//                0就是不放， 1就是放
                if (i >> j & 1) {
//                    如果放置小方块使得连续的空白格子数成为奇数，
//                    这样的状态就是不行的，
                    if (cnt & 1) {
                        st[i] = false;
                        break;
                    }
                }else cnt++;
//                不放置小方格
            }

            if (cnt & 1) st[i] = false;
        }

//        初始化状态数组f
        memset(f, 0, sizeof f);

//        棋盘是从第0列开始，没有-1列，所以第0列第0行，不会有延伸出来的小方块
//        没有横着摆放的小方块，所有小方块都是竖着摆放的，这种状态记录为一种方案
        f[0][0] = 1;
//        遍历每一列
        for (int i = 1; i <= m; i++) {
//            枚举i列每一种状态
            for (int j = 0; j < 1 << n; j++) {
//                枚举i-1列每一种状态
                for (int k = 0; k < 1 << n; k++) {
//                    f[i-1][k] 成功转到 f[i][j]
                    if ((j & k) == 0 && st[j | k]) {
                        f[i][j] += f[i - 1][k]; //那么这种状态下它的方案数等于之前每种k状态数目的和
                    }
                }
            }
        }
//        棋盘一共有0~m-1列
//        f[i][j]表示 前i-1列的方案数已经确定，从i-1列伸出，并且第i列的状态是j的所有方案数
//        f[m][0]表示 前m-1列的方案数已经确定，从m-1列伸出，并且第m列的状态是0的所有方案数
//        也就是m列不放小方格，前m-1列已经完全摆放好并且不伸出来的状态
        cout << f[m][0] << endl;
    }
    return 0;
}

最短hamilton路径

给定一张n个点的带权无向图，点从0~n-1标号，求起点0到终点n-1的最短路径，路径定义从0到n-1不重不漏地经过每一个点恰好一次。
解法思路

1. 起点是0，终点是j，i是一个二进制数，比如(1110011)，表示第一个点第二个点走过了，第三个第四个点没有走过…状态分类是通过倒数第二个点是哪个来分类，比如说，划出来的2，就是说从0走到j，走过的所有点是j的路径中倒数第二个点是2的子集。
2. 假如倒数第2个点是K，那么因为要求0–j的距离最短，k–j的距离是固定的，那么只要让0–k的距离最短即可，又因为0–k走的时候不能走过j点，所以状态要i - {j}，也就是除去第j个点。

for (int i = 0; i < 1 << n; i ++ )
        for (int j = 0; j < n; j ++ ) {
            if (i >> j & 1) {
                for (int k = 0; k < n; k ++ )
                    if ((i - (1 << j)) >> k & 1) {
                        f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
                    }
            }
        }
    cout << f[(1 << n) - 1][n - 1] << endl;

树形DP

没有上司的舞会

有个公司要举行一场晚会。
为了能玩得开心，公司领导决定：如果邀请了某个人，那么一定不会邀请他的上司
（上司的上司，上司的上司的上司……都可以邀请）。
但如何使每个参加晚会的人都能为晚会增添一些气氛，求一个邀请方案，使气氛值的和最大。

我们要思考动态转移方程有两种情况（取和不取）。
用链式结构存储，ed数组存储边的信息，通过ed数组中的next域将所有起点为i的边连成一条链。

struct edge
{
    int v,next;
}ed[24005];
int head[6005],num;
int n,w[6005];
int dp[6005][5],flag[6005];
void find(int u,int v)  //链表建立
{
    ed[++num].v=v;//他的上司 
    ed[num].next=head[u];//下一个 
    head[u]=num;//为了方便下一个找自己 
}//寻根问祖，确定不会和上司相遇，构建基本的数据模型

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct edge
{
    int v,next;
}ed[24005];
int head[6005],num;
int n,w[6005];
int dp[6005][5],flag[6005];
void build(int u,int v)//链表建立
{
    ed[++num].v=v;//他的上司 
    ed[num].next=head[u];//下一个 
    head[u]=num;//为了方便下一个找自己 
}
void dfs(int u)
{
    for(int i=head[u];i!=-1;i=ed[i].next)
    {
        int v=ed[i].v;
        dfs(v);//递归到根部 
        dp[u][0]+=max(dp[v][1],dp[v][0]);//不取这个点，取价值最大的情况
        dp[u][1]+=dp[v][0];//取这个点，他的儿子都不能要 
    }
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    scanf("%d",&w[i]),dp[i][1]=w[i];
    for(int i=1;i<=n-1;i++)
    {
        int u,v;
        scanf("%d%d",&v,&u);
        build(u,v);
        flag[v]=1;//有上司
    }
    for(int i=1;i<=n;i++)
    if(!flag[i])//找到"老大" 
    {
        dfs(i);
        printf("%d",max(dp[i][0],dp[i][1]));//取或不取中找最大
        return 0;
    }
}

记忆DP

滑雪

给定一个R行C列的矩阵，表示一个矩形网格滑雪场。
矩阵中第 i 行第 j 列的点表示滑雪场的第 i 行第 j 列区域的高度。
一个人从滑雪场中的某个区域内出发，每次可以向上下左右任意一个方向滑动一个单位距离。
当然，一个人能够滑动到某相邻区域的前提是该区域的高度低于自己目前所在区域的高度。
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
在给定矩阵中，一条可行的滑行轨迹为24-17-2-1。
在给定矩阵中，最长的滑行轨迹为25-24-23-…-3-2-1，沿途共经过25个区域。
现在给定你一个二维矩阵表示滑雪场各区域的高度，请你找出在该滑雪场中能够完成的最长滑雪轨迹，并输出其长度(可经过最大区域数)。

二维数组初始化的时候最好统一赋值为-1，如果不进行初始化直接用0判断，此题可以，可是如果遇到一些记忆化搜索的问题要求方案数的时候，初始化是0可能会导致个别情况计算出来的恰好结果是0时，却被认为未遍历过，因此统一赋值为-1就没错了其实就是每一次dfs时候是否有flag标记

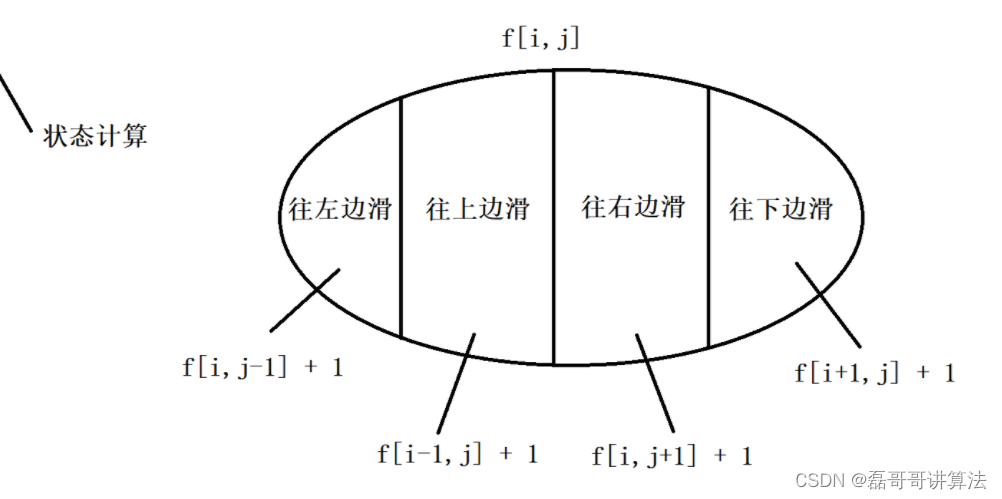
int n, m;
int h[N][N];
int f[N][N];
int dx[4] = { 1,0,-1,0 }, dy[4] = { 0,-1,0,1 };
int dp(int x,int y){
    int &v=f[x][y];   //用引用v来代替f[x][y]
    if(v!=-1) return v; //如果v!=-1，证明v的值已经计算出来了，不用再算了，这一步很关键，省去了多余的计算，不然会TLE
    v=1;  //在滑向第一个区域前，每个点自身算一个区域
    for(int i=0;i<4;i++)   //遍历四个方向
    {
        int a=x+dx[i],b=y+dy[i];
        if(a>=1&&a<=r&&b>=1&&b<=c&&h[x][y]>h[a][b])   //如果滑的方向的区域还在雪场内
            v=max(v,dp(a,b)+1);   //算最大值
    }
    return v;
}
int main(){
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			scanf("%d", &h[i][j]);
	memset(f, -1 ,sizeof f);
	int res = 0;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
			res = max(res, dp(i, j));
	printf("%d", res);
	return 0;
}

结尾

本章基本都是基于DP的模板题，算法模板也很好记忆，主要是考查的是看到问题分解题目状态的思路，里面的滑雪是本科的时候一次结课考试里的题目，整数划分又是我考天津大学的笔试题，继续加油吧。