前缀和与差分数组

适合解决的问题

例：n个数,m次操作。每一次操作都给定区间和数值[l,r]+del.最后有q个询问，问[l,r]点的值或者单点查值。
注：先进行m个修改操作，后进行查询操作。（离线的区间区间修改问题）

差分数组的定义

记录当前位置与上一位置数的差值

for(int i=1;i<=n;i++){
	d[i]=(a[i]-a[i-1]);
}

解释

原数组 a[5]=9,3,5,4,2
差分数组 d[5]=9,-6,2,-1,-2
很容易发现d[i] (从1到i ) 的累加和等于a[i]的值

差分的思想是根据元素与元素的逻辑关系（大小关系），求出某一位置元素的值，对应为[i] (从1到i )的前缀和
a的前缀和 9 12 17 21 23
d的前缀和 9 3 5 4 2
d是s的二阶差分
使用：如果我们在差分数组的 d[x]减去del 在d[y+1]位置处加上del,就能达到整个区间修改的操作

例： 现在对[2,4]加上5
我们要对d[2]+5,d[5]-5
b[i] : 9 ,-1 ,2 ,-1 ,-7
对应的a[i] : 9 , 8 , 10 , 9 , 2
再求出新的前缀和数组s[i]：9 ，17 ，27 ，36 ，38
根据两个前缀和相减，可求a的和
比如s[5]=a[1]+a[2]+a[3]+a[4]+a[5]
s[2]=a[1]+a[2],
求a[3]~a[5]的前缀和呢，就s[5]-s[2]

前缀和的定义

对于原数组a[],s[j]等于a[]从1到j相加

for(int i=1;i<=n;i++){
	s[i]=s[i-1]+a[i];
}

#include<bits/stdc++.h>
using namespace std;
const int maxn=1e5;
int s[maxn],b[maxn],sum[maxn],n,m,last; 
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		int x;
		cin>>x;
//		cin>>a[i];
        b[i]=x-last;//差分数组 
        last=x;
	}
	cin>>m;//m次操作
	for(int i=1;i<=m;i++){
		int l,r,c;
		cin>>l>>r>>c;
		b[l]+=c;
		b[r+1]-=c;
	} 
	for(int i=1;i<=n;i++){
		s[i]=b[i]+s[i-1];
		sum[i]=s[i]+sum[i-1];
	}
	cin>>q;
	for(int i=1;i<=q;i++){
		int l,r;
		cin>>l>>r;
		cout<<sum[r]-sum[l-1]<<endl;
	}
	return 0;
}

二维前缀和与差分

对于一个二维数组a[i][j],它的前缀和s[i][j]==p从0到i,q从0到j的a[p][q]数组
可以想象成矩形相加减去重叠的地方（容斥原理）

for(int i=1;i<=n;i++){
	for(int j=1;j<=m;j++){
		s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
	}
}

二维的差分数组

for(int i=1;i<=n;i++){
	for(int j=1;j<=m;j++){
		d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
	}
}

静态数组的求和问题

sum(l1,l2,s1,s2)=s[r1][r2]-s[l1-1][r2]-s[r1][l2-1]-s[l1-1][l2-1]

int sum(int l1,int r1,int l2,int r2){
	return s[r1][r2]-s[l1-1][r2]-s[r1][l2-1]+s[l1-1][l2-1];
}

进行m次区间修改后的静态单点求值问题

void add(int l1,int r1,int l2,int r2,int x)
{
    d[l1][l2]+=x;
    d[r1+1][l2]-=x;
    d[l1][r2+1]-=x;
    d[r1+1][r2+1]+=x;
}

静态维护区间加多项式的求和问题

现在有这么一类问题就是对数组a进行若干次操作，选定一个[l,r]的区间和一个k次多项式f(x)，a[l]+f(0),a[l+1]+f(1),…,a[r]+f(r-l)
进行m此操作后，让你输出数组每一个位置的值。
等差数列可以看作是f(x)=kx+b的多项式函数，所以也是可以做到的。

预备知识参考

一阶差分的定义： 一阶差分就是离散函数中连续相邻两项之差。当自变量从x变到x+1时，函数y=y(x)的改变量∆y(x)=y(x+1)-y(x)，(x=0，1，2，…)称为函数 y(x)在点x的一阶差分，记为∆y(x)=yx+1-yx，(x=0，1，2，…)。
高阶差分： 定义当自变量从 x变到x+1 时，一阶差分的差分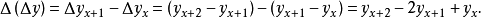称为函数的二阶差分，记作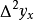
即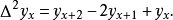
此类推，可得函数的n阶差分为

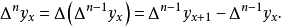
定义k阶向前差分
定义k阶向后差分
定义0阶差分
多项差分的性质：
多项式差分：
对于一个多项式函数f(x),定义它在f(x)的向前差分为∆f(x)=f(x+1)-f(x),在它定义的f(x)一阶向后差分为∆f(x)=f(x)-f(x-1)
数组的前缀和以及差分：对于一个数组a[i]的前缀和s[i]等于0到i的a[]相加
d[i]=a[i]-a[i-1]为差分数组

借教室（二分加差分数组）

这道题使用了二分，将前i天进行二分，运用了差分数组

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e6+10;
int n,m,s[maxn],t[maxn];
ll d[maxn],b[maxn],r[maxn],a[maxn];
bool check(int x){
	memset(b,0,sizeof(b));
	for(int i=1;i<=x;i++){
		b[s[i]]+=d[i];
		b[t[i]+1]-=d[i]; //差分数组 
	}
	ll sum=0;
	for(int i=1;i<=n;i++){
		a[i]=a[i-1]+b[i]; //差分数组的前缀和等于a[i] 
	}
	for(int i=1;i<=n;i++){
		if(r[i]-a[i]<0)
		return false;
	}
	return true;
}
int binary(int l,int r){
	int mid,ans;
	while(l<=r){
		mid=(l+r)>>1;
		if(check(mid))l=mid+1;
		else
		ans=mid,r=mid-1;
	}
	return ans;
}
int main(){
	scanf("%d%d",&n,&m);//天数和订单数量 
	for(int i=1;i<=n;i++){
		scanf("%lld",&r[i]);//借教室的数量 
	}
	for(int i=1;i<=m;i++){
		scanf("%lld%d%d",&d[i],&s[i],&t[i]);//租界的数量、借租开始与结束的天数 
	} 
	if(check(m)){
		cout<<0<<endl;
		return 0;
	}
	cout<<"-1"<<endl;
	printf("%d\n",binary(1,m));
	return 0;
}