前言
本文主要是基于 RNN 来解决 next-item 的会话推荐任务。在传统 LSTM 上进行了创新,提出了一种短期注意力优先模型来解决此问题,它可以用来基于长对话捕获用户的一般兴趣,并根据短期内产生的交互捕获用户目前的偏好。两者共同完成 next-item 的推荐任务。
论文链接:https://dl.acm.org/doi/pdf/10.1145/3219819.3219950
github:https://github.com/uestcnlp/STAMP
1. Methods
1.1 Symbolic Description
会话表示为
S
=
[
s
1
,
s
2
,
…
,
s
N
]
S=[s_1,_s2,\dots,s_N]
S=[s1,s2,…,sN],其中包含了一些列用户和物品产生的交互行为,例如
s
i
s_i
si 表示在会话
s
s
s ,时间戳
t
t
t 产生的一次用户的点击行为。物品集合表示为
V
=
{
v
1
,
v
2
,
…
,
v
∣
V
∣
}
V = \{v_1,v_2,\dots,v_{|V|}\}
V={v1,v2,…,v∣V∣},其中每一个物品对应一个嵌入则全部物品的嵌入可以表示为
X
=
{
x
1
,
x
2
…
,
x
∣
V
∣
}
X=\{\mathbf{x}_1,\mathbf{x}_2\,\dots,\mathbf{x}_{|V|}\}
X={x1,x2…,x∣V∣}。STAMP 模型的最终目的就是根据会话来学习到每一个物品真实的
d
d
d 维的嵌入表示
x
i
∈
R
d
\mathbf{x}_{i}\in\mathbb{R}^d
xi∈Rd,完成对会话的嵌入表示。进而可以实现,给出一个匿名会话,可以根据会话中物品的嵌入特点来预测产生该会话的用户下一个最可能产生交互的物品列表。产生推荐所根据的就是生成的对于所有物品下次点击概率的预测向量取其中 top-k 完成推荐。根据 STAMP 模型框架,作者定义了一个三个学习到的向量的线性积生成最终的评分预测向量:
<
a
,
b
,
c
>
=
∑
i
=
1
d
a
i
b
i
c
i
=
a
T
(
b
⊙
c
)
(1)
<a,b,c>=\sum_{i=1}^da_ib_ic_i=\mathbf{a}^T(\mathbf{b}\odot \mathbf{c})\tag{1}
<a,b,c>=i=1∑daibici=aT(b⊙c)(1)
满足
a
,
b
,
c
∈
R
d
a,b,c\in\mathbb{R}^d
a,b,c∈Rd
1.2 The Short-Term Memory Priority Model

STAMP 模型的基础是短期记忆优先模型( Short-Term Memory Priority model (STMP)),模型框架如图1所示.由图可以看出,
m
s
\mathbf{m}_s
ms 和
m
t
\mathbf{m}_t
mt 作为模型的输入,其中
m
s
\mathbf{m}_s
ms 代表从会话中所提取到的用户兴趣表示,它被定义为所有产生过交互物品嵌入的平均表示:
m
s
=
1
t
∑
i
=
1
t
x
i
(2)
\mathbf{m_s} = \frac{1}{t}\sum_{i=1}^t\mathbf{x}_i\tag{2}
ms=t1i=1∑txi(2)
m
t
\mathbf{m}_t
mt 是用户短期的偏好表示,在这里作者认为会话中最终产生交互的物品嵌入
x
t
\mathbf{x}_t
xt 可以用来表示用户短期偏好,因此直接表示为
m
t
=
x
t
\mathbf{m}_t=\mathbf{x}_t
mt=xt。由此得到的用户长期和短期偏好嵌入表示经过 MLP 进行特征提取分别得到
h
s
\mathbf{h}_s
hs 和
h
t
\mathbf{h}_t
ht。使用简单的 MLP 进行特征抽象,没有隐含层,对
m
s
\mathbf{m}_s
ms 的操作定义为:
h
s
=
f
(
W
s
m
s
+
b
s
)
(3)
\mathbf{h}_s=f(\mathbf{W}_s\mathbf{m}_s+\mathbf{b}_s)\tag{3}
hs=f(Wsms+bs)(3)
其中
h
s
∈
R
d
\mathbf{h}_s \in \mathbb{R}^d
hs∈Rd 代表输出状态。
W
s
∈
R
d
×
d
\mathbf{W}_s \in \mathbb{R}^{d \times d}
Ws∈Rd×d 代表可学习的权重矩阵,
b
s
\mathbf{b}_s
bs 代表偏置矩阵。
f
(
⋅
)
f(\cdot)
f(⋅) 代表非线性激活函数,作者在本文的实验中使用 tanh。基于此对于候选的物品列表中的一个物品嵌入
x
i
∈
V
\mathbf{x}_i \in V
xi∈V 评分函数定义为:
z
^
i
=
σ
(
<
h
s
,
h
t
,
x
i
>
)
(4)
\hat{\mathbf{z}}_i=\sigma(<\mathbf{h}_s,\mathbf{h}_t,\mathbf{x}_i>)\tag{4}
z^i=σ(<hs,ht,xi>)(4)
由此可以看出,本文的逻辑框架非常清晰,就是根据会话生成长期用户偏好嵌入和短期偏好嵌入,再根据实际候选目标物品的嵌入生成下一次产生交互的概率评分。最终的概率要经过一个 softmax,得到最终的预测概率:
y
^
=
s
o
f
t
m
a
x
(
z
^
)
(5)
\hat{\mathbf{y}}=softmax(\hat{\mathbf{z}})\tag{5}
y^=softmax(z^)(5)
对于损失函数的选择则是采用交叉熵损失函数:
L
=
−
∑
i
=
1
∣
V
∣
y
i
l
o
g
(
y
i
^
)
+
(
1
−
y
i
)
l
o
g
(
1
−
y
^
i
)
(6)
\mathcal{L}=-\sum_{i=1}^{|V|}\mathbf{y}_ilog(\hat{\mathbf{y}_i})+(1-\mathbf{y}_i)log(1-\hat{\mathbf{y}}_i)\tag{6}
L=−i=1∑∣V∣yilog(yi^)+(1−yi)log(1−y^i)(6)
使用 SGD 完成梯度下降进行学习
然而,从式(2)可以看出,当建模用户的长期偏好 m s \mathbf{m} _s ms 时是根据会话中产生的所有交互的物品嵌入,也就是说 STMP 模型将会话中的每一项视为同样重要的,但是在长会话中经常会产生以外的点击此时将每一项产生点击的物品嵌入是为同等重要的并不严谨。因此,作者提出了一种注意力模型来解决这一问题。称它为短期注意/记忆优先模型(STAMP)。
3.3 The STAMP Model

从两个模型的框架图可以看出,两种模型的主要不同在于生成用户长期偏好嵌入。STAMP 模型采取注意力机制完成嵌入过程。该模型的注意力机制包括两个部分:
- (1)一个简单的前馈神经网络( FNN )负责生成每个物品在会话中的注意力系数
- (2)基于注意力权重系数生成注意力加权表示的 m a \mathbf{m}_a ma
用于注意力计算的前馈神经网络( FNN )定义为:
α i = W 0 σ ( W 1 x i + W 2 x t + W 3 m s + b a ) (7) \alpha_i=\mathbf{W}_0\sigma(\mathbf{W}_1\mathbf{x}_i+\mathbf{W}_2\mathbf{x}_t+\mathbf{W}_3\mathbf{m}_s+\mathbf{b}_a)\tag{7} αi=W0σ(W1xi+W2xt+W3ms+ba)(7)
其中 x i ∈ R d \mathbf{x}_i \in\mathbb{R}^d xi∈Rd 代表会话 s s s 中的第 i i i 个物品的嵌入也就是满足 s i ∈ S s_i \in S si∈S。 x t ∈ R d \mathbf{x}_t \in\mathbb{R}^d xt∈Rd 代表会话中最后一次点击物品的嵌入。 W 0 ∈ R 1 × d , W 1 , W 2 , W 3 ∈ R d × d \mathbf{W}_0 \in \mathbb{R}^{1\times d},\mathbf{W}_1,\mathbf{W}_2,\mathbf{W}_3\in\mathbb{R}^{d \times d} W0∈R1×d,W1,W2,W3∈Rd×d 代表可学习的权重矩阵。基于此我们看出通过当前物品嵌入 x i \mathbf{x}_i xi,最后的物品的嵌入 x t \mathbf{x}_t xt,全局的物品平均嵌入 m s \mathbf{m}_s ms 我们可以得到当前物品对于该会话的注意力系数 α i \alpha_i αi。需要注意的是,式(7)中明确考虑了短期记忆,这也是为什么该注意力模型被称为短期注意优先模型的原因。
在得到当前会话中每一个物品的注意力系数后,可以根据会话中的每一个物品得到长期偏好的最终嵌入表示:
m
a
=
∑
i
=
1
t
α
i
x
i
(8)
\mathbf{m}_a=\sum_{i=1}^t\alpha_i\mathbf{x}_i\tag{8}
ma=i=1∑tαixi(8)
1.4 The Short-Term Memory Only Model
为了验证本文提出的短期注意力优先模型的有效性,作者还提出了一种只有短期注意的网络模型( Short-Term Memory Only (STMO))。该模型对于 next-item 的预测只给予最终产生过交互的物品嵌入
s
t
s_t
st。也就是说只有
h
t
\mathbf{h}_t
ht,并且也只使用了一层的简单 MLP 进行特征提取:
h
t
=
f
(
W
t
x
t
+
b
t
)
(9)
\mathbf{h}_t=f(\mathbf{W}_t\mathbf{x}_t+\mathbf{b}_t)\tag{9}
ht=f(Wtxt+bt)(9)
最终的物品得分表示为
z
^
i
=
h
t
T
x
i
(10)
\hat{\mathbf{z}}_i=\mathbf{h}_t^T\mathbf{x}_i\tag{10}
z^i=htTxi(10)
2. Experiments



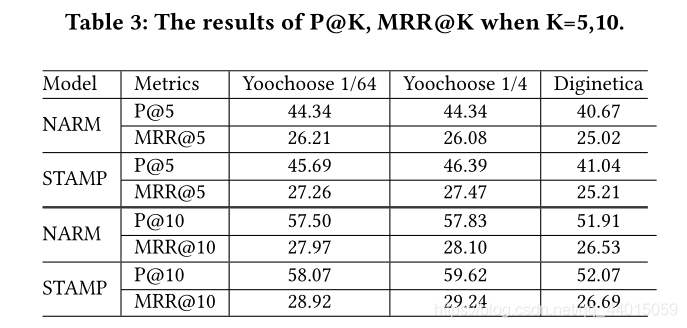
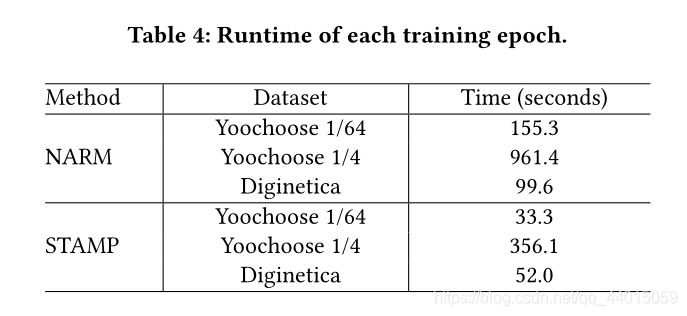










 本文介绍了如何利用RNN改进传统的LSTM,提出短期注意力优先模型(STAMP)来解决会话推荐任务。STAMP通过短期和长期用户兴趣的结合,预测用户在会话中的下一步交互物品。模型引入了注意力机制,以更准确地捕捉会话中的重要交互。实验表明,STAMP在推荐准确性上优于仅依赖短期记忆的模型。
本文介绍了如何利用RNN改进传统的LSTM,提出短期注意力优先模型(STAMP)来解决会话推荐任务。STAMP通过短期和长期用户兴趣的结合,预测用户在会话中的下一步交互物品。模型引入了注意力机制,以更准确地捕捉会话中的重要交互。实验表明,STAMP在推荐准确性上优于仅依赖短期记忆的模型。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








