最优控制问题求解

典型的动态优化问题（也称为最优控制问题）求解 ，常用于轨迹优化。

1. 问题描述

目标函数：
$\min \text{Cost}={\sum }_{k=2}^{11}(x_k-1{)}^2+{\sum }_{k=1}^{10}{u}_k^2$

约束条件：

1. 状态方程： $x[n+1]=0.8\ast x[n]+u[n]$
2. 控制输入： $u[n]\in [-2,2]$
3. 初始状态： $x[1]=0$

2. scipy求解

首先利用scipy求解，思路类似于连续系统情况下的打靶法 (shooting method)，即优化变量是离散（时间上）的控制输入，目标函数和约束条件都表示为控制输入的函数。

import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# 定义时间区间和初始条件
N = 10
x0 = 0
x = np.zeros(N+1)
x[0] = x0

# 定义目标函数
def objective(u):
    for i in range(N):
        x[i+1] = 0.8*x[i] + u[i]
    return np.sum((x[1:]-1)**2) + np.sum(u**2)

# 定义约束条件
cons = ({'type': 'ineq', 'fun': lambda u:  2 - u},
        {'type': 'ineq', 'fun': lambda u:  u + 2})

# 初始猜测
u0 = np.zeros(N)

# 求解
sol = minimize(objective, u0, method='SLSQP', constraints=cons)

# 打印结果
print(f"Optimal control sequence: {sol.x}")
print(f"Minimum loss value: {sol.fun}")
if sol.success:
    print("Optimization was successful.")
else:
    print(f"Optimization failed: {sol.message}")

# 绘图
# 使用之前求解得到的控制输入
u = sol.x

# 计算状态轨迹
x = np.zeros(N+1)
x[0] = x0
for i in range(N):
    x[i+1] = 0.8*x[i] + u[i]

# 绘制状态轨迹
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.plot(range(N+1), x, 'o-')
plt.title('State Trajectory')
plt.xlabel('Time step')
plt.ylabel('State')

# 绘制控制输入
plt.subplot(1, 2, 2)
plt.plot(range(N), u, 'o-')
plt.title('Control Input')
plt.xlabel('Time step')
plt.ylabel('Control input')

plt.tight_layout()
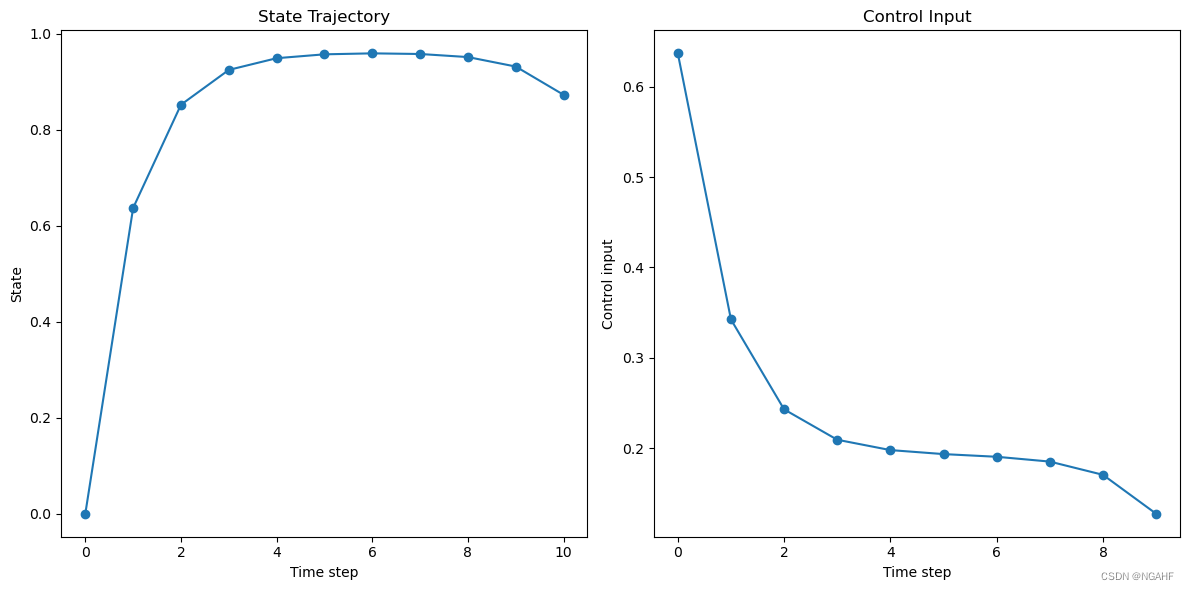
plt.show()

输出：

Optimal control sequence: [0.63698059 0.34243414 0.24294484 0.20931517 0.19786525 0.1934362 0.19046757 0.18514381 0.1705031  0.12745731]
Minimum loss value: 1.0088266500834469
Optimization was successful.

3. 贪心求解

import numpy as np
import matplotlib.pyplot as plt

# 定义参数
N = 10  # 时间步数
x = np.zeros(N+1)  # 状态变量
u = np.zeros(N)  # 控制输入
u_min, u_max = -2, 2  # 控制输入的范围
x[0] = 0  # 初始状态
cost = 0

# 定义一步损失
def one_step_cost(x, u):
    return np.sum((x - 1)**2) + np.sum(u**2)

# 定义状态更新函数
def update_state(x, u):
    return 0.8 * x + u

# 贪心算法求解
for k in range(N):
    best_obj = np.inf
    best_u = None
    for u_k in np.linspace(u_min, u_max, 100):  # 在控制输入的范围内搜索
        x_next = update_state(x[k], u_k)
        obj = one_step_cost(x_next, u_k)
        if obj < best_obj:
            best_obj = obj
            best_u = u_k
    u[k] = best_u
    x[k+1] = update_state(x[k], u[k])
    cost += best_obj

print("最优控制输入：", u)
print("最优状态：", x)
print("最终代价：", cost)

# 绘图
# 绘制状态轨迹
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.plot(range(N+1), x, 'o-')
plt.title('State Trajectory')
plt.xlabel('Time step')
plt.ylabel('State')

# 绘制控制输入
plt.subplot(1, 2, 2)
plt.plot(range(N), u, 'o-')
plt.title('Control Input')
plt.xlabel('Time step')
plt.ylabel('Control input')

plt.tight_layout()
plt.show()

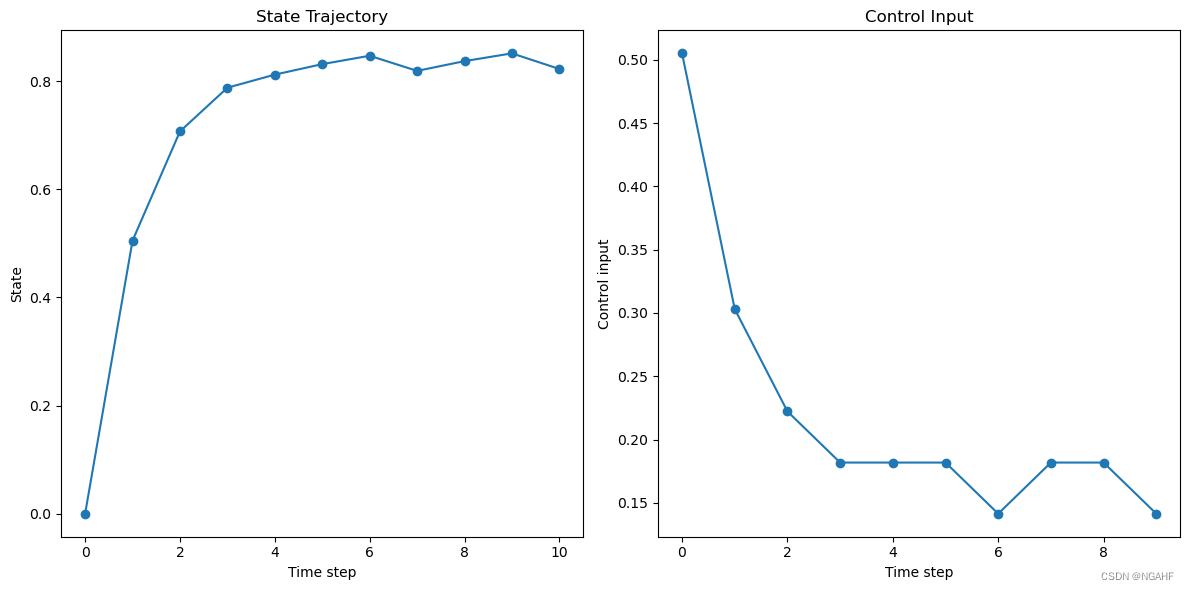
输出

最优控制输入： [0.50505051 0.3030303  0.22222222 0.18181818 0.18181818 0.18181818 0.14141414 0.18181818 0.18181818 0.14141414]
最优状态： [0. 0.50505051 0.70707071 0.78787879 0.81212121 0.83151515 0.8470303  0.81903838 0.83704889 0.85145729 0.82257998]
最终代价： 1.1772775333335328

4. cvxpy求解

最后利用cvxpy求解，求解思路类似于连续情况下的配点法 (collocation)，即优化变量是离散（时间上）的控制输入和状态变量，目标函数和约束条件均表示为离散控制输入和状态变量的函数。

import cvxpy as cp
import matplotlib.pyplot as plt
# 定义时间步长和时长
T = 10  # 总时间步长
dt = 1.0  # 单位时间步长

# 定义状态变量和控制变量
x = cp.Variable((T+1, 1))  # 状态变量：位置
u = cp.Variable(T)  # 控制变量：加速度

# 动态模型约束
dynamics_constraints = []
cost = 0
for t in range(T):
    # 基本的运动学方程：x[t+1] = 0.8 * x[t] + u[t]
    dyn_constr_equ = x[t+1, 0] == 0.8 * x[t, 0] + u[t]
    dynamics_constraints += [dyn_constr_equ, cp.norm(u[t],'inf')<=2]
    cost += cp.sum_squares(x[t + 1]-1) + cp.sum_squares(u[t])

# 初始条件和终止条件
initial_conditions = [x[0, 0] == 0]  # 初位置

# 成本函数（例如，最小化控制能量总和）
objective = cp.Minimize(cost)

# 求解最优控制问题
problem = cp.Problem(objective, dynamics_constraints + initial_conditions)
problem.solve()

# 打印结果
print("最优状态变量:")
print(x.value)
print("最优控制变量:")
print(u.value)
print('最终代价：', problem.value)

# 绘图
# 绘制状态轨迹
plt.figure(figsize=(12, 6))

plt.subplot(1, 2, 1)
plt.plot(range(T+1), x.value, 'o-')
plt.title('State Trajectory')
plt.xlabel('Time step')
plt.ylabel('State')

# 绘制控制输入
plt.subplot(1, 2, 2)
plt.plot(range(T), u.value, 'o-')
plt.title('Control Input')
plt.xlabel('Time step')
plt.ylabel('Control input')

plt.tight_layout()
plt.show()

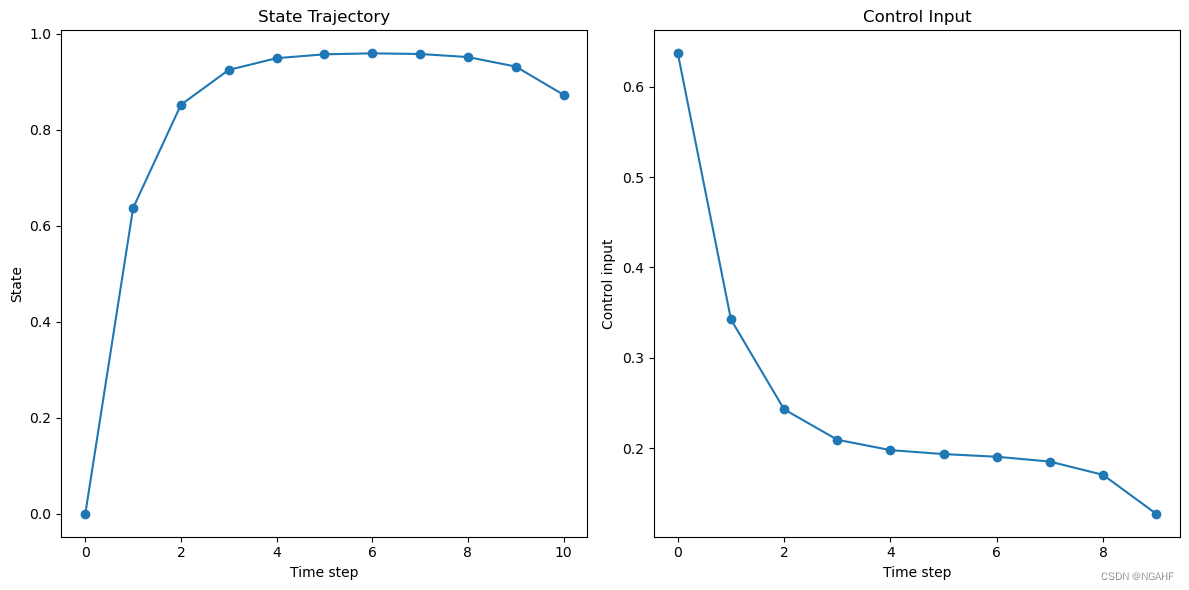
输出

最优状态变量: [[6.05901594e-10] [6.36957512e-01] [8.51959787e-01] [9.24509784e-01] [9.48922497e-01] [9.56934454e-01] [9.58961201e-01] [9.57637505e-01] [9.51242564e-01] [9.31462954e-01] [8.72585183e-01]]
最优控制变量: [0.63695751 0.34239378 0.24294195 0.20931467 0.19779646 0.19341364 0.19046854 0.18513256 0.1704689  0.12741482]
最终代价： 1.0088265717021232

5. 小结

method	cost
scipy	1.0088266500834469
贪心	1.1772775333335328
cvxpy	1.0088265717021232