为什么刚度阵对称？根本原因在于物理方程。知识点：矩阵微积分，物理方程

为什么刚度阵对称？根本原因就是以上的物理方程。当物理方程发生变化，刚度阵便不一定能对称。例如下面链接里提到的非线性情况，
https://www.zhihu.com/question/398632114

我对市面上现有教材的意见

大多数书上会这样描述刚度阵对称的原因：

其中W为应变能的密度。
但是，以上的式子实际是不充分的证明，式子本身没有错，但是没有写出关键的过程。
如果仅按照张量理论，即在忽略$\epsilon 与\sigma 的关系$的状况下直接去计算应变能密度对应变的混合偏导，无论是先对${\epsilon }_i还是{\epsilon }_j求偏导，最后的结果都是\frac{1}{2}{C}_{ij}+\frac{1}{2}{C}_{ji}$。具体过程可以见我的github笔记（有专门针对矩阵求导的笔记）。
但是，如果考虑了物理方程，情况截然不同。我们直接有$$\frac{\partial W}{\partial {\epsilon }_i}={\sigma }_i$$
这是通过物理方程，将W写成完全以应变分量为自变量的形式再求偏导得到的。依据：
来自《弹性力学》徐芝纶第十一章《变分法》。之后，由
$${\sigma }_i=C_{ij}{\epsilon }_j$$

方可以得到刚刚教材中的：
替换一下角标就能得到

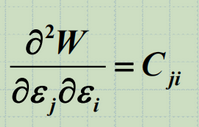
我的有关解决这个问题的笔记链接：
https://github.com/BraveDrXuTF/WhyCisSYMMETRIC