实对称矩阵的特征值求法_机械振动理论(3)-解析实模态分析

最新推荐文章于 2023-04-06 15:23:44 发布

weixin_39855568

最新推荐文章于 2023-04-06 15:23:44 发布

阅读量1.7k

点赞数

文章标签：实对称矩阵的特征值求法

模态分析是一种研究系统振动特性的分析方法，可以分为：解析模态分析和试验模态分析。

解析法，在事先知道结构的几何形状、边界条件和材料特性的前提下，将结构的质量分布、刚度分布和阻尼分布分别用质量矩阵、刚度矩阵和阻尼矩阵表示出来，这样便有了足够的信息来确定系统的模态参数（固有频率、阻尼系数、模态振型）。理论证明，这些模态参数可以完整地描述系统的动力学特性。
实验法，从测量结构（样机）上某些点的动态输入力和输出响应开始。并且一般还要将测量得到的数据转换成频响函数，即作为频率函数的输出输入之比。理论证明，这些频响函数可以用模态参数表示。因此实验模态分析的第二步就是从测得的频响函数来估计这些模态参数。

不管是哪种模态分析，都需要满足以下几点假设：

线性假设：结构的动态特性是线性的，就是说任何输入组合引起的输出等于各自输出的组合，其动力学特性可以用一组线性二阶微分方程来描述。每次进行模态分析时，应当首先检查结构的线性动态特性（将在后面涉及如何操作）。
时不变假设：结构的动态特性不随时间而变化，因而微分方程的系数是与时间无关的常数。由于不得不安装在结构上的运动传感器的附加质量，可能出现典型的时不变问题。
可观测假设：这意味着用以确定所关心的系统动态特性所需要的全部数据都是可以观测的。为了避免出现可观测性问题，合理选择响应自由度是非常重要的。
此外还常常假设结构遵从Maxwell互易定理，即在q点输入所引起的p点的响应等于p点相同输入引起的q点的响应。此假设使得质量矩阵、刚度矩阵、阻尼矩阵和频响函数矩阵都成了对阵矩阵。多输入试验允许对所测的频响函数做互易性检查。

在机械振动理论(2)-多自由度系统中，用到的模态分析方法实际上是解析复模态分析，适用于各种阻尼形式。

为了从数学角度揭示模态分析的本质，这里主要针对两自由度系统解析实模态分析方法（实模态：对于满足或假设满足无阻尼或比例阻尼的系统的振动模态，振动系统中各点的相位差为

或

，模态振型系数为实数

^[1]）进行整理与总结。

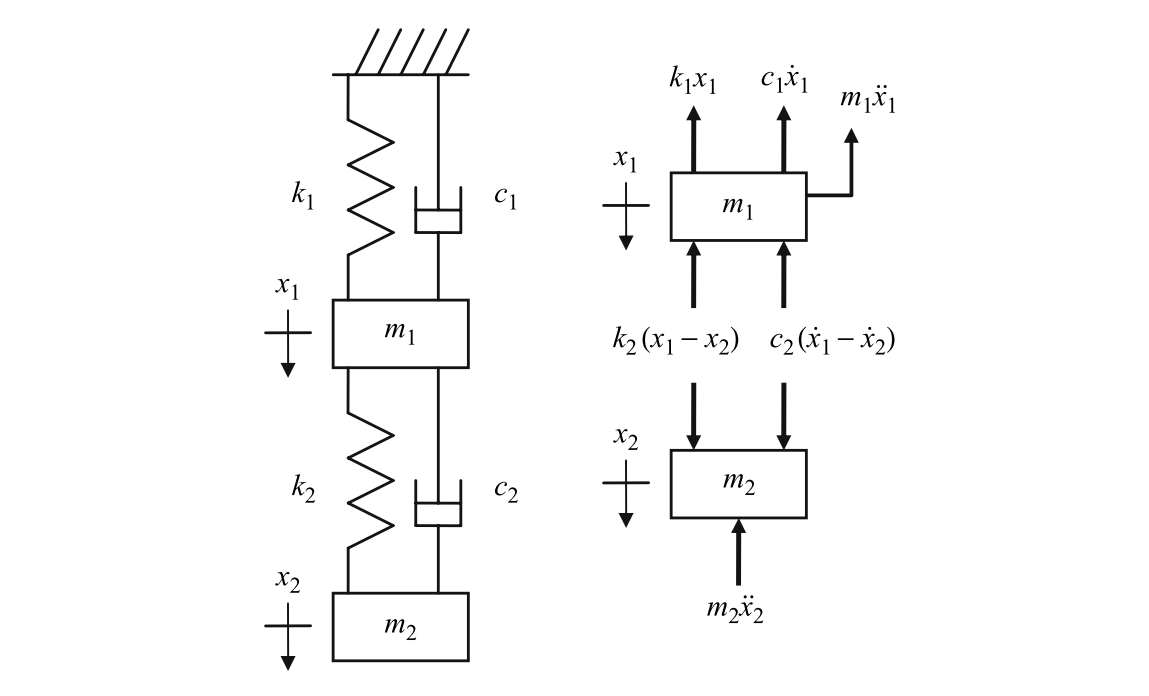
例如，下图是一个由弹簧-质量块-阻尼器串联构成的两自由度振动系统，假设是粘性阻尼：

两自由度比例阻尼系统

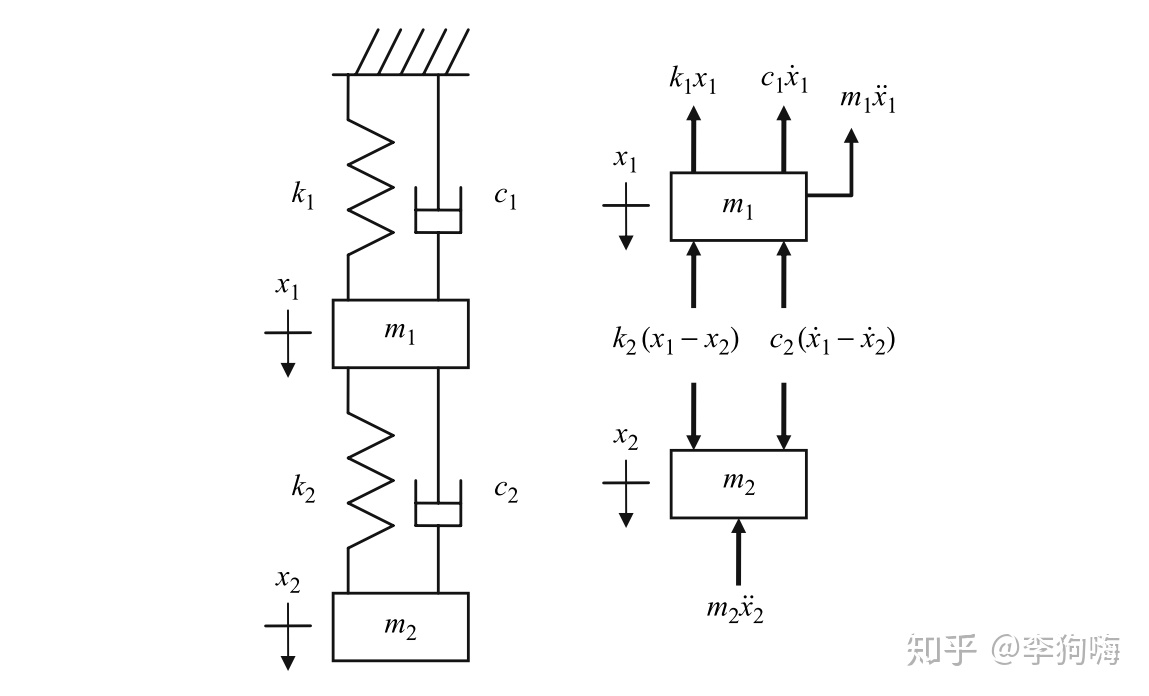
在自由振动情况下（无外力施加），根据Newton第二定律，该系统的动力学微分方程组如下：

写成矩阵形式为：

或者：

其中，

和

分别为质量矩阵、阻尼矩阵、刚度矩阵和位移向量。

接下来的任务是想得到该系统各个坐标在每一时刻的位移，也就是式

的解。

式

是二阶常系数线性微分方程组，其时域解具有

自然指数形式

，详见：如何推导高阶常系数线性常微分方程的解具有自然指数形式的充分必要条件？

且对于每个二阶常系数线性微分方程，其对应的解均为两个指数呈复共轭的自然指数函数的线性组合。参考：高等数学齐次微分方程的通解形式。依据欧拉公式

，详见："上帝公式"(欧拉公式)真的神到无法触碰？，两个指数呈复共轭的

自然指数函数的线性组合可以写为以一个固有频率振动的简谐运动形式，由此可知：对于两自由度系统（对应两个二阶常系数线性微分方程），其每个坐标的振动位移均可视为两个简谐运动 线性叠加的结果。

对于实模态分析，这里假设其阻尼满足粘性比例阻尼，即

。那么在这种情况下，就可以在

忽略阻尼项的情况下寻找 特征值和 特征向量（后面会涉及到），且该特征向量也可以使得阻尼矩阵解耦。 ^[2]

将其自然指数形式解

带入到式

中，

代表坐标

的振动幅值和方向，

并忽略阻尼项，并两边除以非零项

，得到：

为了得到式

的解，一种情况是令

，得到了

平凡解（trivial solution），是我们不太关心的。另一种情况是令

，也是我们主要关心的情况。

根据线性代数中的克莱姆法则，由
个方程构成的

元齐次线性方程组的系数行列式不为零时，齐次方程组只有零解（平凡解）。

所以如果式

具有非零解（非平凡解），那么系数矩阵的行列式必须为零。

该行列式称为该振动系统的特征方程或特征多项式。

通过线性代数知识可以得到矩阵

的

特征值和 特征向量。这里的 特征值对应于振动的 固有频率的平方， 特征向量对应于振动的振型。

展开式

，得到：

对于该两自由度振动系统，在不考虑重根的情况下，具有两个不同的特征值，并且每个特征值对应一个特征向量。假设两个特征值分别为：

和

，那么固有频率为：

且这里规定，

也就是说，单自由度系统具有一个固有频率；两自由度系统具有两个固有频率，以此类推。并且，对于两自由度系统，每个固有频率都对应一种特征变形模式，该变形模式也称为模态振型。

模态振型表示的是：各个物理坐标间的相对振动幅度和方向。

对于该两自由度系统，为了找到系统的模态振型，可以将特征值

和

代入方程组中的任意一个方程中（不管代入哪个方程结果都一样，因为当式

成立时，两个方程线性相关，仅相差一个比例系数，而每个振型本身就是

一个可缩放的且各个元素相对大小保持不变系数列）。

但是，可以根据自己的需求对模态振型进行归一化，在试验模态分析中，通常是以激励点的坐标为参考进行归一化。

这里选择方程组中上面的方程：

并以坐标

为参考点进行归一化，那么根据式

振动幅值和方向归一化后有：

那么，代入第一个特征值

，将得到第一阶模态振型：

那么，代入第二个特征值

，将得到第二阶模态振型：

在振动时，该两自由度系统会按照这两个振动频率和振型的线性组合振动，其具体组合形式取决于实际初始条件，但固有频率和振型都是系统的固有属性，与外界输入无关。

同理，如果以坐标

为参考点进行归一化，那么根据式

振动幅值和方向归一化后有：

那么，代入第一个特征值

，将得到第一阶模态振型：

那么，代入第二个特征值

，将得到第二阶模态振型：

为了直观，用PPT做了个示意动画：

模态振型

现在代入具体数值及初始条件来计算一个实例：

还是同样对于这个两自由度系统，令

，

。

的初始条件为：

，

；

的初始条件为：

，

得运动方程：

得到特征多项式为：

解得两个特征值：

；

，对应两个固有频率：

；

以

为参考进行归一化，并选择方程组中上面的方程：

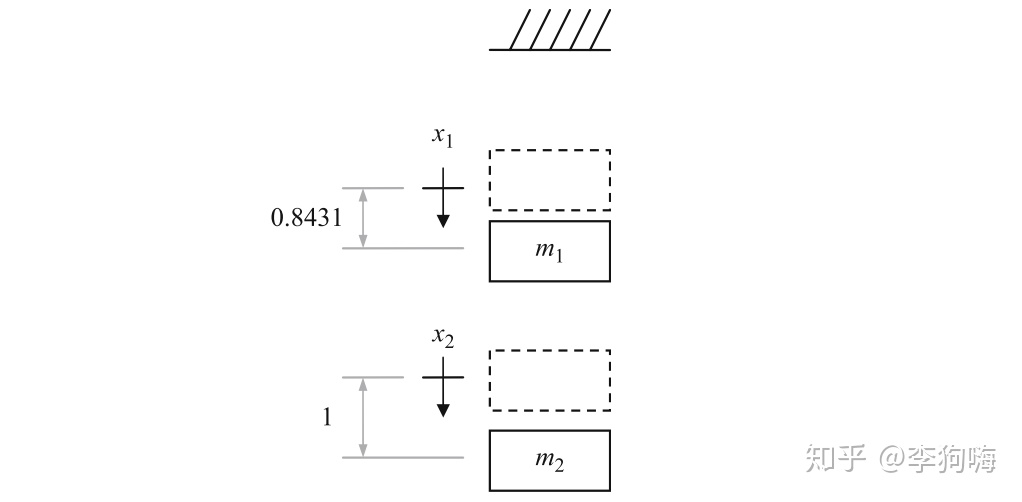
代入第一个特征值得到第一阶模态为：

该振型可以这样解读：当坐标

运动

个单位位移时，坐标

同向（同相位）运动

个单位位移。

第一阶振型

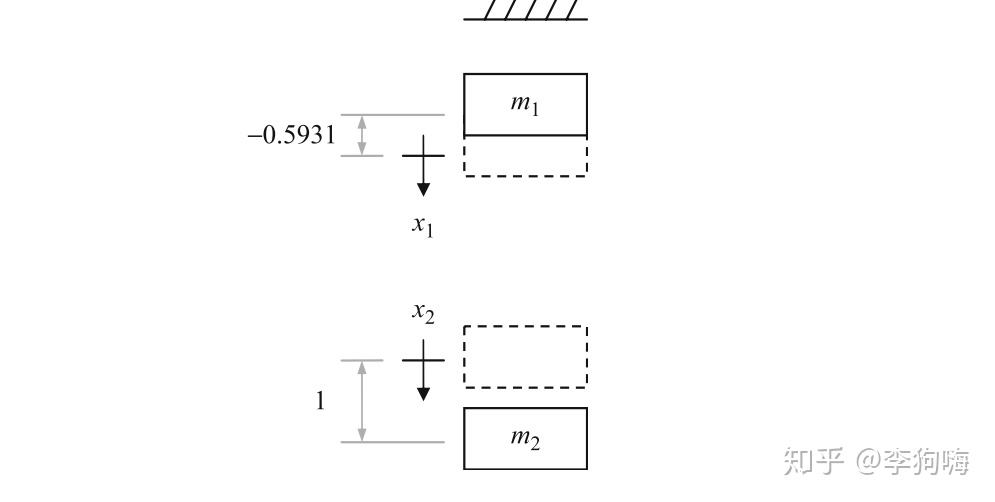
代入第二个特征值得到第二阶模态为：

该振型可以这样解读：当坐标

运动

个单位位移时，坐标

反向（反相位）运动

个单位位移。

第二阶振型

在机械振动理论(1)-单自由度系统中，得到单自由度欠阻尼系统的时域解形式为^[3]：

其中系数

由初始条件决定，其与

互为一对复共轭，

表示衰减率，

则表示阻尼振动频率。

而对于该两自由度系统，如果先忽略阻尼项，考虑无阻尼情况，即式

，

各个坐标的时域通解形式为：

因为式

中各个

复指数项代入后都能够使得式

成立

，不妨简写为：

对于

代表坐标，

代表模态。

该解的形式说明：总的振动是各个模态振动的线性叠加效果。

解的一阶导数为：

代入初始条件：

应用模态振型

及

，可以将式

缩减为只含有

个未知量的方程组：

解得：

代入式

得：

根据Euler公式，有：

，有：

上面的结果说明，两自由度的系统可能以第一阶固有频率振动，可能以第二阶固有频率振动，也可能是两种固有频率振动的线性组合，实际要看初始条件如何。

前面的计算虽然用到了特征值和特征向量，但还不是严格意义上的模态分析法。

下面介绍的是通过解析模态分析法求解

前面已经计算的特征值和特征向量，将特征向量按列排布就得到所谓的模态振型矩阵：

对于模态分析，特征向量之间的正交性是一个重要性质，可以将第一个特征值（第一阶固有频率）及其对应的第一个特征向量（第一阶模态振型）代入到式

中，有：

展开为：

左乘第二阶模态振型的转置有：

由于，

为对称矩阵，因此左右均转置有（因为

）：

同理有：

比较式

和

，有：

因为这里假设没有重特征根，所以

，因此有：

和

成立。

即：

但是，

其中，

和

分别为第

阶的模态质量和模态刚度。

所以有：

实现了方程之间的解耦，就可以用单自由度的知识进行求解。

代入具体数值，

解耦后的方程组：

这里采用了坐标变换：

，或写为

而：

那么，可以将原物理坐标系下的初始条件变换到模态坐标上去：

由机械振动理论(1)-单自由度系统中的推导可知，对于无阻尼系统，单自由度系统的时域解为：

所以模态位移为：

和

。

要得到物理坐标系下的位移值，则需要再做一次坐标变换，将模态坐标：

所以有：

可以看出，在该初始条件下，系统振动是两种模态振动的叠加效果。

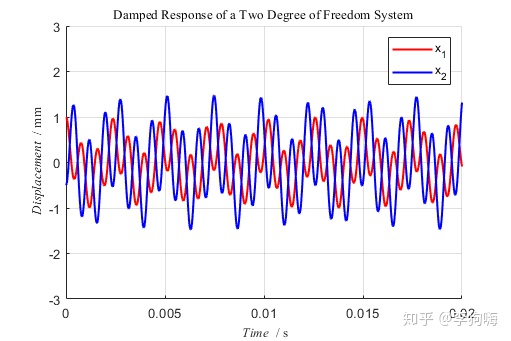
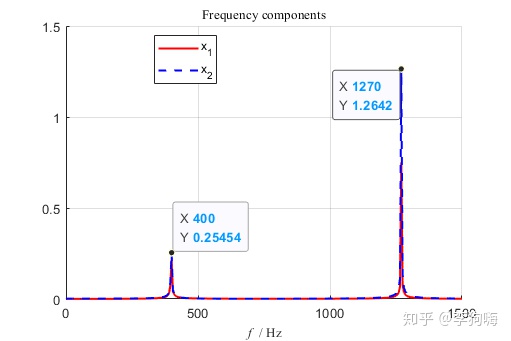
做快速傅里叶变换有：

那么存在系统只以一种模态（一种固有频率和振型）振动的情况吗？

答案是：存在的。关键在于如何设定初始条件。

如果选择的初始条件恰好匹配了一阶模态振型，那么系统将只以这一个固有频率振动。

例如该例子，如果初始条件是：

，

；

，

. 注意，该初始位移与第一阶振型匹配（即，同比例）。那么将该初始位移转化到模态坐标下是：

那么，在模态坐标下的时域解为

：

再转换到物理坐标系去：

结果有：

即，在该初始条件下，系统只以第一阶固有频率振动。可以看出两个坐标的位移同向。

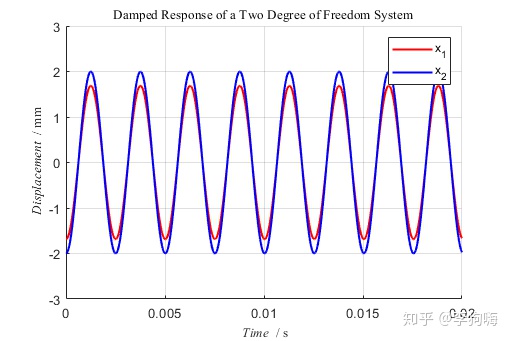
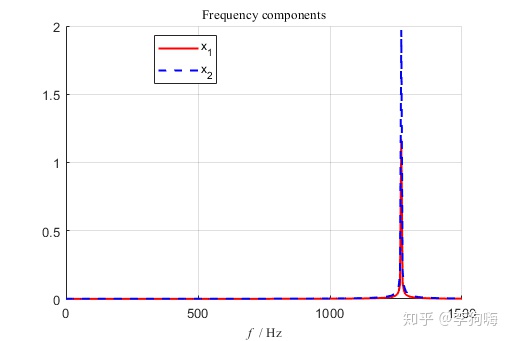
做快速傅里叶变换有：

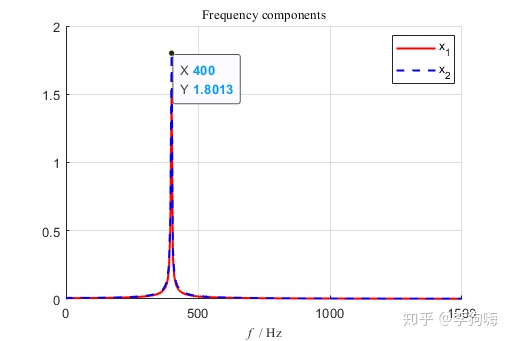
同理，如果初始条件是：

，

；

，

. 注意，该初始位移与第二阶振型匹配（即，同比例）。那么在该初始条件下，系统只以第二阶固有频率振动。可以看出两个坐标的位移反向。

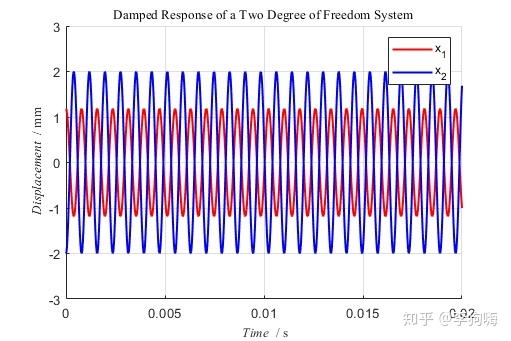
做快速傅里叶变换有：

最后，考虑一下阻尼存在的情况。

对于无主动阻尼器的一般机械振动系统而言，阻尼很小，所以将其近似为比例阻尼是可以被接受的，比例阻尼意味着各个坐标之间的相位差为

或

，模态振型系数为实数。

如果是比例阻尼，有

，且

为实数。

这样在模态分析寻找特征值和特征向量的过程中可以先将阻尼忽略。只需要在后面计算出模态阻尼矩阵：

。

证明：

因此可得到完全解耦的，考虑阻尼的模态运动方程：

而单自由度系统的时域解中也将阻尼考虑了进去：

其他的步骤都与上述例子中的处理方法一致。

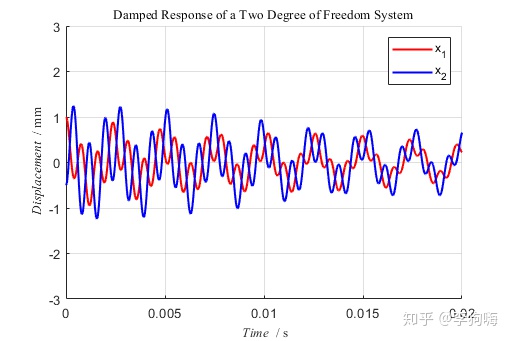
另外，在处理特征向量的时候，通常会采用单位模态质量归一化法，得到较为常见的模态振型形式，为后续计算提供方便。

Matlab 代码

clear

参考

^傅志方, 华宏星. 模态分析理论与应用[M]. 上海交通大学出版社, 2000.
^T.L. Schmitz, K.S. Smith, Machining Dynamics, springer, Springer US, Boston, MA, 2009.
^T.L. Schmitz, K.S. Smith, Mechanical Vibrations, Springer, Springer US, Boston, MA, 2012.