【卡尔曼滤波第四期上】多变量卡尔曼滤波

原创于 2025-07-03 16:06:41 发布 · 960 阅读

18 ·

CC 4.0 BY-SA版权

文章标签：

#KF

机器学习原理及代码实现专栏收录该内容

19 篇文章

订阅专栏

前言

本教程处理的是线性卡尔曼滤波（Linear KF），LKF假设系统动态模型是线性的。
截至目前，我们已经处理过一维问题，例如估计液体温度。但是许多动态过程有2、3甚至更多个维度。

比如，用于描述在三维空间中运行的飞机的位置的状态向量：[x, y, z]
描述飞机位置和速度的状态向量是六维的：
描述飞机位置、速度和加速度的状态向量则是九维的：
在这里插入图片描述
假设匀加速运动模型，我们可以用九个运动方程在 n−1 时刻来外插飞机在 n 时刻的状态：

必要的背景知识

矩阵运算

向量和矩阵的加法和乘法
矩阵转置
逆矩阵（不需要知道怎么求逆，只需要知道逆矩阵是什么即可）
对称矩阵
特征值和特征向量

期望的代数运算

在推导卡尔曼滤波方程时会大量用到期望的代数运算。如果你感兴趣并想深入理解推导过程，就需要掌握期望代数。

基本期望代数运算法则

期望记为大写字母 E，随机变量的期望 E(X)，等于该随机变量的均值：
E(X)=μX，其中 μX 是该随机变量的均值。

以下是一些基本的期望代数运算法则：
在这里插入图片描述
方差和协方差的期望的代数运算法则

下表总结了方差和协方差的期望的代数运算法则。
在这里插入图片描述
方差和协方差的期望的代数运算法则不是很直观，这里不做解释，有需要可自行学习，或查看对应教程-卡尔曼滤波简介-必要的背景知识。

多变量正态分布

我们知道卡尔曼滤波的输出是一个随机变量，该随机变量的均值描述了状态的估计，方差描述了状态估计的不确定性。即卡尔曼滤波同时提供了状态估计和状态估计的可信程度。

一维卡尔曼滤波方程包含四个描述不确定性的变量：

pn,n 是当前估计值的方差
pn+1,n 是（对下一时刻）预测值的方差
rn 是测量值的方差
q 是过程噪声

对多变量卡尔曼滤波而言，系统状态是通过向量描述的。比如平面上运动的物体需要两个变量来描述：x方向位置和y方向位置：

此时卡尔曼滤波的输出就是一个多维随机变量。它的不确定性通过 协方差矩阵 描述。

多变量卡尔曼滤波中描述不确定性的变量对应为：

Pn,n 是描述估计值不确定性的协方差矩阵
Pn+1,n 是描述预测值不确定性的协方差矩阵
Rn 是描述测量值不确定性的协方差矩阵
Q 是描述过程噪声的协方差矩阵

协方差

协方差 是对两个或两个以上随机变量的 相关程度 的度量。

假设给定 x−y 平面上一个物体的一系列测量值。
在这里插入图片描述
由于存在随机误差，这些测量值存在方差。来看看几种不同的测量值分布示意：

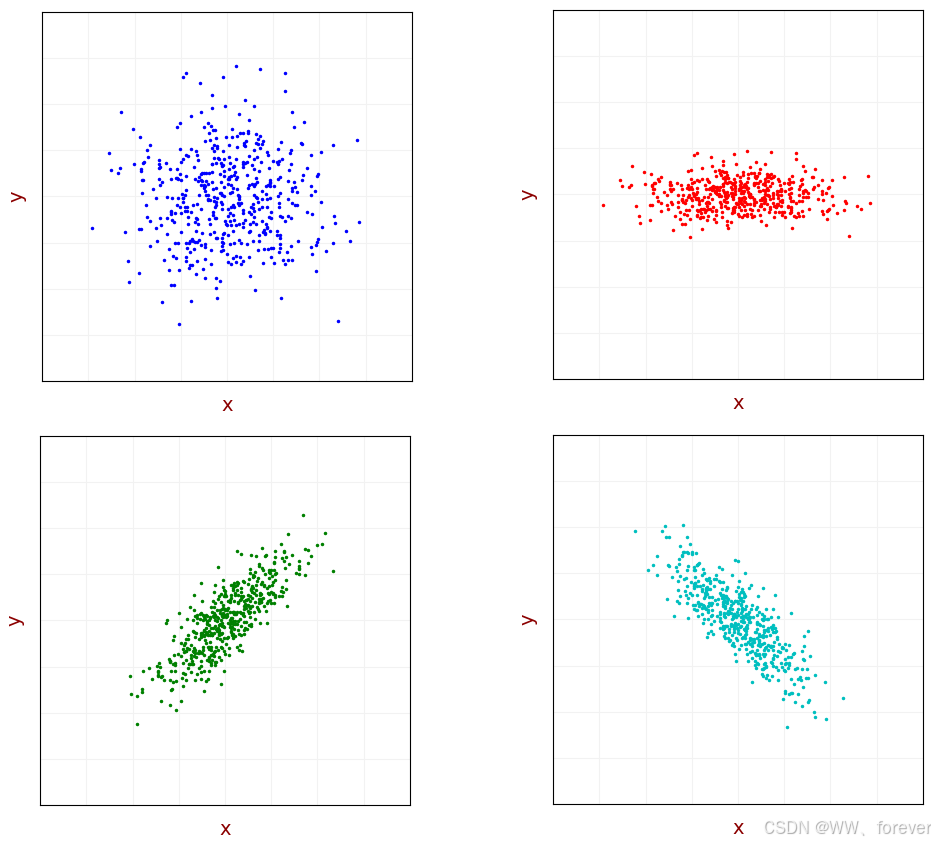
上两个图描述的是不存在相关的测量值分布。x 的取值不依赖于 y。蓝色的测量分布图中 x 和 y 具有相同的方差，所以整个样本分布的形状大致是个圆。对于红色的测量分布图，x 的分布方差比 y 更大，因此样本分布形状是个椭圆。

由于两个方向上的测量没有关联，因此 x 和 y 的协方差是0。

下两个图描述的是存在相关的测量值分布，即x 和 y 之间存在相关性。绿色的分布图中 x 取较大值时对应的 y 取值也较大，反之亦然，因此具有正相关性，故协方差也为正。而青色的分布图中 x 取较大值时对应的 y 取值会较小，反之亦然，因此具有负相关性，故协方差也为负。

对 N 个给定的 X 和 Y 的总体（译注：总体 Population，指某个变量对应的全量样本，即所有可能取值的集合），其之间的 协方差 如下计算：
在这里插入图片描述
把总体协方差公式变换一下：

N 个样本（译注：样本 Sample，是总体的一个真子集）的协方差以 N−1 来归一化：

把样本协方差公式变换一下：
在这里插入图片描述

协方差矩阵

协方差矩阵是一个方阵，描述一系列随机变量两两之间的协方差。

对于一个二维随机变量，协方差矩阵为：
在这里插入图片描述
对 n 维随机变量，其协方差矩阵为：

python 示例如下：

import numpy as np

x = np.array([2, 3, -1, 4])
y = np.array([8, 7, 9, 6])

C = np.cov(x,y)
print(C)

[[ 4.66666667 -2.66666667]
 [-2.66666667  1.66666667]]

MATLAB 示例如下：

x = [2 3 -1 4];
y = [8 7 9 6];

C = cov(x,y)

C =

    4.6667   -2.6667
   -2.6667    1.6667

协方差矩阵的性质
在这里插入图片描述

协方差矩阵和期望
在这里插入图片描述

多变量正态分布

单变量正态分布 通过一个钟形的高斯曲线描述：
在这里插入图片描述

正态分布记为：N(μ,σ²)
在这里插入图片描述

多变量正态分布是单变量正态分布在多维随机变量情况时的推广。

n 维多变量正态分布记为：
在这里插入图片描述

双变量正态分布

双变量（二维）正态分布描述了两个具有正态分布的随机变量。我想围绕双变量正态分布进行后续讲述，因为二维是我们所能可视化的最高的维度了。

下图是二维高斯函数的图像：
在这里插入图片描述

置信区间

置信区间描述了一个样本落到单变量正态分布的均值附近的概率。

对单变量正态分布，高斯函数在 μ±1σ 区间内的面积是全部面积的 68.26%。
在这里插入图片描述
对单变量正态分布，有如下的性质：

68.26% 对应的置信区间是 1σ
95.44% 对应的置信区间是 2σ
99.74% 对应的置信区间是 3σ

双变量正态分布的概率密度函数以一个二维高斯函数的围成体积来描述。

例如，二维高斯函数在 1σ 对应的水平切片内部围成的体积是围成总体积的39.35%。
二维高斯函数的水平切片向下下投影形状为一个椭圆。
在这里插入图片描述

协方差椭圆

首先，我们看看协方差椭圆的性质。协方差椭圆是高斯分布的一条特殊等高线，使我们能以二维形式展示 1σ
置信区间，从而从几何角度直观解释协方差矩阵。

任何椭圆可以由四个参数描述：

椭圆心 μx,μy
半长轴 a
半短轴 b
朝向角 θ

在这里插入图片描述
椭圆心是随机变量的均值：

椭圆半长轴和半短轴长度是对应随机变量协方差矩阵的特征值的平方根：

半长轴长度 a 是最大的特征值平方根
半短轴长度 b 是第二大的特征值的平方根

椭圆的朝向由随机变量协方差矩阵的特征向量给出：
在这里插入图片描述
使用计算工具可以计算出协方差椭圆的各项参数：

python 示例如下：

import numpy as np

C = np.array([[5, -2],[-2, 1]]) # define covariance matrix

eigVal, eigVec = np.linalg.eig(C) # find eigenvalues and eigenvectors

a = np.sqrt(eigVal[0]) # half-major axis length
b = np.sqrt(eigVal[1]) # half-minor axis length

# ellipse  orientation  angle
theta = np.arctan(eigVec[1, 0] / eigVec[0, 0])

MATLAB 示例如下：

C = [5 -2; -2 1]; % define covariance matrix

[eigVec, eigVal] = eig(C); % find eigenvalues and eigenvectors


if eigVal(1,1) > eigVal(2,2) % get the highest eigenvalue index

    a = sqrt(eigVal(1,1)); % half-major axis length
    b = sqrt(eigVal(2,2)); % half-minor axis length

    theta = atan(eigVec(2,1) / eigVec(1,1));  % ellipse angle (radians)
else

    a = sqrt(eigVal(2,2)); % half-major axis length
    b = sqrt(eigVal(1,1)); % half-minor axis length

    theta = atan(eigVec(2,2) / eigVec(2,1));  % ellipse angle (radians)
end