分位数回归的求解

分位数回归

分位数回归实际上是一种特殊的${\ell }_1$回归问题，特别地，当所求分位数$\tau =0.5$时就是中位数回归。

1 线性规划

1.1 将分位数回归看做是线性规划问题来求解

一般的，线性回归问题可以写为${\ell }_p$范数线性回归，简称为${\ell }_p$回归:
$$\underset{x\in {\mathbb{R}}^n}{\mathrm{argmin}}||\mathbf{A}\mathbf{x}-\mathbf{b}|{|}_p$$
其中$\mathbf{A}\in {\mathbb{R}}^{m\times n},b\in {\mathbb{R}}^m$，$||v|{|}_p=({\sum }_i|{\mathbf{v}}_i{|}^p{)}^{1/p}$表示${\ell }_p$范数
那么从中位数回归的角度来看，损失函数就是绝对损失($p=1$):
$$\underset{x\in {\mathbb{R}}^n}{\mathrm{argmin}}||\mathbf{A}\mathbf{x}-\mathbf{b}||$$
考虑一个两参数的分位数回归优化问题
$$\begin{array}{c}\hat{\beta }=\underset{(b_0,b_1)\in {\mathbb{R}}^2}{\mathrm{argmin}}\left\{\sum _{i=1}^n|y_i-b_0-b_1{x}_i|\right\}\end{array}$$
$\tau$分位数时更一般的形式
$$\hat{\beta }(\tau )=\underset{\mathbf{b}\in {\mathbb{R}}^{m\times n}}{\mathrm{argmin}}\sum _{i=1}^n{\rho }_{\tau }(y_i-{\mathbf{x}}_i^{\top }\mathbf{b})$$
其中$\tau \in (0,1)$是分位数. ${\rho }_{\tau }(\cdot )$是check function(又称检查函数):
$${\rho }_{\tau }(u)=u(\tau -I(u<0))$$
定义${\epsilon }_i=y_i-{\mathbf{x}}_i^{\top }\mathbf{b}$为第$i$个残差，则优化目标$(1)$可以转化为残差的形式
$$\begin{array}{c}\hat{\beta }=\underset{(b_0,b_1)\in {\mathbb{R}}^2}{\mathrm{argmin}}\left\{\sum _{i=1}^n{\epsilon }_i\right\}\end{array}$$
将上式改写：
$$\begin{array}{c}\sum _{i=1}^n{\rho }_{\tau }(\epsilon {}_i)=\sum _{i=1}^n\tau {\epsilon }_i^{+}+(1-\tau )|{\epsilon }_i^{-}|\end{array}$$
由于分位数回归使用的是绝对损失函数，残差恒正，所以将其拆分为正部${\epsilon }_i^{+}=u_i={\epsilon }_{i}I(y_i-{\mathbf{x}}_i^{\top }\mathbf{b}>0),{\epsilon }_i^{-}=v_i={\epsilon }_{i}I(y_i-{\mathbf{x}}_i^{\top }\mathbf{b}<0)$
可见，回归残差的正部被赋予了$\tau$权重，负部被赋予$(1-\tau )$的权重，令$\tau =0.5$就是等权，所以中位数回归又是分位数回归的一个特例。

Figure 1: tau=0.5和 tau=0.9时的check function的图像

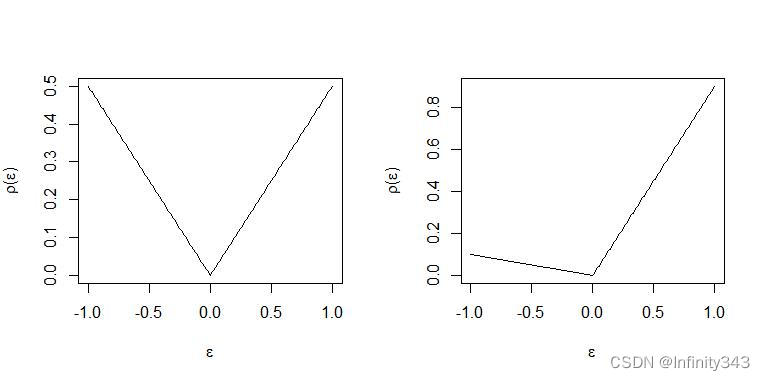
不难看出，${\ell }_1$回归问题在零点处不可导，所以OLS方法不可用，但可以将其划为线性回归问题进行求解。对于一个线性规划问题其标准形式为
$$\begin{gathered} \underset{z}{\min }{c}^{\top }z \\ \mathrm{subject}\mathrm{to}\mathbf{A}z={\mathbf{b}}^{\ast },z\ge 0 \end{gathered}$$
这里的$b^{\ast }$带上星号是为了区分开回归参数$b$. 从定义来看，线性回归标准型要求所有决策变量大于零，显然残差是有正有负的，为满足上述条件，回忆之前对残差正负部的定义：
$${\epsilon }_i=u_i-v_i$$
其中正部$u_i=\max (0,{\epsilon }_i)$负部$v_i=\max (0,-{\epsilon }_i)=|{\epsilon }_i|I_{\epsilon <0}$。
此时式(3)改写为
$$\sum _{i=1}^n{\rho }_{\tau }({\epsilon }_i)=\sum _{i=1}^n{u}_i\tau +v_i(1-\tau )=\tau 1_n^{\top }\mathbf{u}+(1-\tau )1_n^{\top }\mathbf{v}$$
其中$\mathbf{u}=(u_1,\dots ,u_n{)}^{\top },\mathbf{v}=(v_1,\dots ,v_n{)}^{\top }$, $1_n$是$n\times 1$的全一向量。为记号方便，之后的向量或矩阵将不再加粗，而是通过取消下标来表示。若样本量为$N$参数个数为$K$，令$u,v$为松弛变量，则会有$N$个等式约束
$$y_i-x_i^{\top }b={\epsilon }_i=u_i-v_{i}i=1,\dots N$$
上式就可以改写为一个线性规划：
$$\underset{b\in {\mathbb{R}}^K,u\in {\mathbb{R}}_{+}^N,v\in {\mathbb{R}}_{+}^N}{\min }\left\{\tau 1_N^{\top }u+(1-\tau )1_N^{\top }v\mid y_i=x_{i}b+u_i-v_i,i=1,\dots ,N\right\}$$
注意到，上式中参数$b\in {\mathbb{R}}^K$不能保证非负，所以也需要将$b$分解为正负部
$$b=b^{+}-b^{-}$$
其中$b^{+}=\max (0,b),b^{-}=\max (0,-b)$, 该$N$个等式约束以矩阵表达(更直观)：
$$y:=\left[\begin{array}{c}{y}_1\\ ⋮\\ y_N\end{array}\right]=\left[\begin{array}{c}{\mathbf{x}}_1^{\top }\\ ⋮\\ {\mathbf{x}}_N^{\top }\end{array}\right]\left(b^{+}-b^{-}\right)+{\mathbf{I}}_{N}u-{\mathbf{I}}_{N}v$$
其中${\mathbf{I}}_N=diag(1_N)$.将$\mathbf{x}$写为矩阵继续简化表达
$$\mathbf{X}\left(b^{+}-b^{-}\right)+{\mathbf{I}}_{N}u-{\mathbf{I}}_{N}v=\left[\mathbf{X},-\mathbf{X},{\mathbf{I}}_N,-{\mathbf{I}}_N\right]\left[\begin{array}{c}{b}^{+}\\ b^{-}\\ u\\ v\end{array}\right]$$
可以看到现在我们有$N$个等式约束，$2K$个参数(因为参数被分为了正负部，所以乘2)，另外还有$2N$个松弛变量：
$$A:=[\mathbf{X}-\mathbf{X}{\mathbf{I}}_N-{\mathbf{I}}_N]$$
符合标准型的约束条件为：
$$b^{\ast }=A\left[\begin{array}{c}{b}^{+}\\ b^{-}\\ u\\ v\end{array}\right]=Az$$
因为$b^{+}$和$b^{-}$仅通过约束影响最小化问题(优化目标中并不存在$b$)，所以必须引入维度为$2K\times 1$的 $0$ 作为系数向量 $c$ 的一部分，可以适当地定义为
$$c=\left[\begin{array}{c}0\\ \tau 1_N\\ (1-\tau )1_N\end{array}\right]$$
这样目标函数就是
$$c^{\top }z=\underset{=0}{\underbrace{0^{\top }\left(b^{+}-b^{-}\right)}}+\tau 1_N^{\top }u+(1-\tau )1_N^{\top }v=\sum _{i=1}^N{\rho }_{\tau }\left({\epsilon }_i\right).$$

1.1.1 编程实现

显然此时已经识别出了线性规划标准型的所有因素，利用R或python就可以实现求解

getwd()
setwd('C:/Users/beida/Desktop')
base=read.table("rent98_00.txt",header=TRUE)
attach(base)
library(quantreg)
library(lpSolve)
tau <- 0.5


# only one covariate
X <- cbind(1, base$area)  #设计阵X
K <- ncol(X)   #列数量，即参数个数
N <- nrow(X)   #行数量，即样本量(等式约束量)

A <- cbind(X, -X, diag(N), -diag(N)) #优化系数
c <- c(rep(0, 2*ncol(X)), tau*rep(1, N), (1-tau)*rep(1, N))  #目标函数系数
b <- base$rent_euro  #响应变量Y
const_type <- rep("=", N) #N个等式约束

linprog <- lp("min", c, A, const_type, b)
beta <- linprog$sol[1:K] - linprog$sol[(1:K+K)] #
beta


rq(rent_euro ~ area, tau=tau, data=base)

可以看到线性规划求解的结果与quantreg包的rq函数得到了相同的解。
python同理

import io

import numpy as np
import pandas as pd
import requests
np.


url = "http://freakonometrics.free.fr/rent98_00.txt"
s = requests.get(url).content
base = pd.read_csv(io.StringIO(s.decode('utf-8')), sep='\t')


tau = 0.5

from cvxopt import matrix, solvers

X = pd.DataFrame(columns=[0, 1])
X[1] = base["area"]  # data points for independent variable area
#X[2] = base["year"]  # data points for independent variable year
X[0] = 1  # intercept

K = X.shape[1]
N = X.shape[0]

# equality constraints - left hand side

A1 = X.to_numpy()  # intercepts & data points - positive weights
A2 = X.to_numpy() * -1  # intercept & data points - negative weights
A3 = np.identity(N)  # error - positive
A4 = np.identity(N) * -1  # error - negative

A = np.concatenate((A1, A2, A3, A4), axis=1)  # all the equality constraints

# equality constraints - right hand side
b = base["rent_euro"].to_numpy()

# goal function - intercept & data points have 0 weights
# positive error has tau weight, negative error has 1-tau weight
c = np.concatenate((np.repeat(0, 2 * K), tau * np.repeat(1, N), (1 - tau) * np.repeat(1, N)))

# converting from numpy types to cvxopt matrix

Am = matrix(A)
bm = matrix(b)
cm = matrix(c)

# all variables must be greater than zero
# adding inequality constraints - left hand side
n = Am.size[1]
G = matrix(0.0, (n, n))
G[:: n + 1] = -1.0

# adding inequality constraints - right hand side (all zeros)
h = matrix(0.0, (n, 1))

# solving the model
sol = solvers.lp(cm, G, h, Am, bm, solver='glpk')

x = sol['x']

# both negative and positive components get values above zero, this gets fixed here
beta = x[0:K] - x[K : 2 * K]

print(beta)

• 思考
  从R的运行情况来看，线性规划的求解速度显著慢于rq函数，这与求解方法有关。rq提供了以下方法来求解分位数回归：

the algorithmic method used to compute the fit. There are several options:

• “br” The default method is the modified version of the Barrodale and Roberts algorithm for
  $l_1$-regression, used by l1fit in S, and is described in detail in Koenker and d’Orey(1987, 1994), default = “br”. This is quite efficient for problems up to several thousand observations, and may be used to compute the full quantile regression process. It also implements a scheme for computing confidence intervals for the estimated parameters, based on inversion of a rank test described in Koenker(1994).

• “fn” For larger problems it is advantageous to use the Frisch–Newton interior point method “fn”. This is described in detail in Portnoy and Koenker(1997).

• “pfn” For even larger problems one can use the Frisch–Newton approach after preprocessing “pfn”. Also described in detail in Portnoy and Koenker(1997), this method is primarily well-suited for large n, small p problems, that is when the parametric dimension of the model is modest.

• “sfn” For large problems with large parametric dimension it is often advantageous to use method “sfn” which also uses the Frisch-Newton algorithm, but exploits sparse algebra to compute iterates. This is especially helpful when the model includes factor variables that, when expanded, generate design matrices that are very sparse. At present options for inference, i.e. summary methods are somewhat limited when using the “sfn” method. Only the option se = “nid” is currently available, but I hope to implement some bootstrap options in the near future.

• “fnc” Another option enables the user to specify linear inequality constraints on the fitted coefficients; in this case one needs to specify the matrix R and the vector r representing the constraints in the form Rb \geq rRb≥r. See the examples below.

• “conquer” For very large problems especially those with large parametric dimension, this option provides a link to the conquer of He, Pan, Tan, and Zhou (2020). Calls to summary when the fitted object is computed with this option invoke the multiplier bootstrap percentile method of the conquer package and can be considerably quicker than other options when the problem size is large. Further options for this fitting method are described in the conquer package. Note that this option employs a smoothing form of the usual QR objective function so solutions may be expected to differ somewhat from those produced with the other options.

• “pfnb” This option is intended for applications with large sample sizes and/or moderately fine tau grids. It uses a form of preprocessing to accelerate the solution process. The loop over taus occurs inside the Fortran call and there should be more efficient than other methods in large problems.

• “qfnb” This option is like the preceeding one except that it doesn’t use the preprocessing option.

• “ppro” This option is an R prototype of the pfnb and is offered for historical/interpretative purposes, but probably should be considered deprecated.

• “lasso” There are two penalized methods: “lasso” and “scad” that implement the lasso penalty and Fan and Li smoothly clipped absolute deviation penalty, respectively. These methods should probably be regarded as experimental. Note: weights are ignored when the method is penalized.

可见求解方法之多，运行速度也不尽相同。但需要注意的是对于当前问题，单纯形法是很难甚至是无法求解的

simplex(c, A3 = A, b3 = b, maxi = TRUE,  n.iter =200, eps = 1e-4)

> No feasible solution could be found

我们只选取了两个回归系数，样本量为4571，单纯形法的计算时间就超过了5分钟，且没有得到可行解(尽管降低了解的精度要求)。
后续将继续更新别的求解算法。

1.2 扩展(加权分位数回归)

加权分位数回归的思想是基于普通的线性分位回归，作为其的扩展新式，我们首先回顾分位回归的标准线性规划形式：
$$\underset{b\in {\mathbb{R}}^K,u\in {\mathbb{R}}_{+}^N,v\in {\mathbb{R}}_{+}^N}{\min }\left\{\tau 1_N^{\top }u+(1-\tau )1_N^{\top }v\mid y_i=x_{i}b+u_i-v_i,i=1,\dots ,N\right\}$$
其中残差的正负部除了被分配的$\tau$和$1-\tau$之外，系数为$1_N^{\top }$。思考这样一个问题，如果将系数改变，那么上述规划问题就成为了残差不等全问题：
$$\underset{(b,\mathbf{u},\mathbf{v})\in R^K\times R_{+}^{2n}}{\min }\left\{\tau {\mathbf{w}}^{\mathrm{T}}\mathbf{u}+(1-\tau ){\mathbf{w}}^{\mathrm{T}}\mathbf{v}\mid {\mathbf{x}}^{\top }b+\mathbf{u}-\mathbf{v}=\mathbf{y}\right\}$$
其中$\mathbf{w}=w_1,\dots ,w_n$是$n\times 1$的权重向量。
证明：
首先有目标函数
$$\underset{\left(b,e_i\right)\in R^K\times R_{+}^n}{\min }\left\{\sum _{i=1}^n{w}_i{\rho }_{\tau }\left(y_i-x_i^{\top }b\right)\mid e_i=y_i-x_i^{\top }b\right\}$$
把$x_i^{\top }\beta$记为$q$来简化表达，这样$u$和$v$的定义变为：
$$u_i=\{\begin{array}{ll}{y}_i-q& \text{ for }{y}_i>q,\\ 0& \text{ otherwise }\end{array}{v}_i=\{\begin{array}{ll}-\left(y_i-q\right)& \text{ for }{y}_i<q,\\ 0& \text{ otherwise }\end{array}$$
则有损失函数(loss function):
$$\begin{array}{rl}R(q)& =\sum _{i=1}^n{w}_i{\rho }_{\tau }\left(y_i-q\right)\\ & =\sum _{y_i<q}{w}_i(\tau -1)\left(-v_i\right)+\sum _{y_i\ge q}{w}_i\left(\tau u_i\right)\\ & =(1-\tau )\sum _{i=1}^n{w}_i{v}_i+\tau \sum _{i=1}^n{w}_i{u}_i\\ & =(1-\tau ){\mathbf{w}}^{\mathrm{T}}\mathbf{v}+\tau {\mathbf{w}}^{\mathrm{T}}\mathbf{u}\end{array}$$
其中$\mathbf{w}=(w_i,\dots ,w_n{)}^{\top },\mathbf{u}=(u_1,\dots ,u_n{)}^{\top }$, $\mathbf{v}=(v_1,\dots ,v_n{)}^{\top }$
$$e_i=y_i-q=u_i-v_i,i=1,\dots ,n.$$
约束条件改为
{ e 1 = y 1 − q e 2 = y 2 − q ⋯ e n = y n − q → { u 1 − v 1 = y 1 − q u 2 − v 2 = y 2 − q ⋯ u n − v n = y n − q → { q + u 1 − v 1 = y 1 q + u 2 − v 2 = y 2 ⋯ q + u n − v n = y n → { 1 n q + u − v = y } \left\{\begin{array} { l } { e _ { 1 } = y _ { 1 } - q } \\ { e _ { 2 } = y _ { 2 } - q } \\ { \cdots } \\ { e _ { n } = y _ { n } - q } \end{array} \rightarrow \left\{\begin{array} { l } { u _ { 1 } - v _ { 1 } = y _ { 1 } - q } \\ { u _ { 2 } - v _ { 2 } = y _ { 2 } - q } \\ { \cdots } \\ { u _ { n } - v _ { n } = y _ { n } - q } \end{array} \rightarrow \left\{\begin{array} { l } { q + u _ { 1 } - v _ { 1 } = y _ { 1 } } \\ { q + u _ { 2 } - v _ { 2 } = y _ { 2 } } \\ { \cdots } \\ { q + u _ { n } - v _ { n } = y _ { n } } \end{array} \quad \rightarrow \left\{\mathbf{1}_{n} q+\mathbf{u}-\mathbf{v}=\mathbf{y}\right\}\right.\right.\right. ⎩ ⎨ ⎧​e1​=y1​−qe2​=y2​−q⋯en​=yn​−q​→⎩ ⎨ ⎧​u1​−v1​=y1​−qu2​−v2​=y2​−q⋯un​−vn​=yn​−q​→⎩ ⎨ ⎧​q+u1​−v1​=y1​q+u2​−v2​=y2​⋯q+un​−vn​=yn​​→{1n​q+u−v=y}
所以有：
$$\underset{(q,\mathbf{u},\mathbf{v})\in R\times R_{+}^{2n}}{\min }\left\{\tau {\mathbf{w}}^{\mathrm{T}}\mathbf{u}+(1-\tau ){\mathbf{w}}^{\mathrm{T}}\mathbf{v}\mid 1_{n}q+\mathbf{u}-\mathbf{v}=\mathbf{y}\right\}$$
很明显加权是对于$\mathbf{u}$和$\mathbf{v}$而言的，那么1.1节中的规划算法仍然适用，而问题转变为了如何选择权重. Huang(2015)的建议是:

(i) For bivariate symmetrically distributed data, we suggest the first weighting scheme:
$$w_i\left(x_i,\tau \right)=\{\begin{array}{ll}\frac{{\mathrm{e}}^{x_i}}{T_1},& \tau \le 0.5,\\ \frac{{\mathrm{e}}^{-x_i}}{T_2},& \tau >0.5\end{array}$$
where $T_1={\sum }_{i=1}^n{\mathrm{e}}^{x_i},T_2={\sum }_{i=1}^n{\mathrm{e}}^{-x_i}$, and both ensure that all weights add up to 1 .
(ii) For multivariate data with positive values, we suggest the second weighting scheme:
$$w_i\left({\mathbf{x}}_i\right)=\frac{\Vert {\mathbf{x}}_i\Vert }{T},$$
where ${\mathbf{x}}_i={\left(x_{i1},\dots ,x_{ik}\right)}^{\mathrm{T}},\Vert {\mathbf{x}}_i\Vert =\sqrt{{\sum }_{j=1}^k{x}_{ij}^2}$, and $T={\sum }_{i=1}^n\Vert {\mathbf{x}}_i\Vert$. Here, $w_i\left({\mathbf{x}}_i\right),i=1,\dots ,n$ are not dependent on $\tau$.

1.2.1 R实现

还是使用相同的数据集与设定

getwd()
setwd('C:/Users/beida/Desktop')
base=read.table("rent.txt", header=TRUE)
library(quantreg)
library(lpSolve)

tau <- 0.5

# only one covariate
X <- cbind(1, base$area)  #设计阵X
Y <- base$rent_euro
K <- ncol(X)   #列数量，即参数个数
N <- nrow(X)   #行数量，即样本量(等式约束量)

W = rep(1, N)
#W = exp(X[, 1])/sum(exp(X[, 1]))
TT = 0
for (i in 1:dim(X)[1]){
  W_T = sqrt(X[i,1]^2 + X[i,2]^2)

  TT = TT + W_T
}
for (i in 1:dim(X)[1]){
  W[i] =  sqrt(X[i,1]^2 + X[i,2]^2)/TT
}

A <- cbind(X, -X, diag(N), -diag(N)) #优化系数
c <- c(rep(0, 2*ncol(X)), tau*rep(1, N)*W, (1-tau)*rep(1, N)*W)  #目标函数系数


const_type <- rep("=", N) #N个等式约束

linprog <- lp("min", c, A, const_type, Y)
beta <- linprog$sol[1:K] - linprog$sol[(1:K+K)] #
beta

rq('rent_euro ~ area', tau=tau, weights = W, data=base)
rq('rent_euro ~ area', tau=tau, weights = NULL, data=base)
plot(X[,2], Y)
abline(rq('rent_euro ~ area', tau=tau, weights = W, data=base), col='blue')
abline(rq('rent_euro ~ area', tau=tau, weights = NULL, data=base), col='red')
abline(lm(base$rent_euro ~ base$area), col='yellow')

为了对比计算结果，我们同时使用了rq函数，并给定相同的权重

这是线性规划的计算结果

rq函数的计算结果

可见二者结果是相同的，将他们得到的回归直线画出来

黄线是条件均值回归，蓝线是加权分位回归，红线是普通分位回归，由于后两者之间的斜率差距很小，直线差别不大

参考文献

• [1] Huang, M. L., Xu, X., & Tashnev, D. (2015). A weighted linear quantile regression. Journal of Statistical Computation and Simulation, 85(13), 2596-2618.
• [2] Koenker, R., & Hallock, K. F. (2001). Quantile regression. Journal of economic perspectives, 15(4), 143-156.
• [3] Koenker, R., Chernozhukov, V., He, X., & Peng, L. (Eds.). (2017). Handbook of quantile regression.
• [4] Koenker, R. (2017). Quantile regression: 40 years on. Annual review of economics, 9, 155-176.

---

2 GCD

本次将介绍另一个${\ell }_1$回归问题的求解方法：贪婪坐标下降(Greedy Coordinate Descent, GCD)。
在这之前，先引入一些前导内容

2.1 拉普拉斯分布(Laplace disribution)

• pdf
  一个服从$\mathrm{Laplace}(\mu ,b)$的随机变量$X$, 其pdf为：
  $$f_X(x|\mu ,b)=\frac{1}{2b}\exp \left(-\frac{|x-\mu |}{b}\right)$$
  其中$\mu$是位置参数, $b>0$是尺度参数. 很明显，当$\mu =0,b=1$拉普拉斯分布就是$\theta =1/2$的指数分布。
• cdf

$$\begin{array}{rl}F(x)& ={\int }_{-\infty }^{x}f(u)\mathrm{d}u=\{\begin{array}{ll}\frac{1}{2}\exp \left(\frac{x-\mu }{b}\right)& \text{ if }x<\mu \\ 1-\frac{1}{2}\exp \left(-\frac{x-\mu }{b}\right)& \text{ if }x\ge \mu \end{array}\\ & =\frac{1}{2}+\frac{1}{2}\mathrm{sgn}(x-\mu )\left(1-\exp \left(-\frac{|x-\mu |}{b}\right)\right)\end{array}$$

• 逆cdf：
  $$F^{-1}(p)=\mu -b\mathrm{sgn}(p-0.5)\ln (1-2|p-0.5|).$$

2.2 MLE

$n$个iid样本的联合似然函数:
$$L(\mu ,b)={\left(\frac{1}{2b}\right)}^n\exp \left(-\frac{{\sum }_i^N|x_i-\mu |}{b}\right)$$
对数联合似然(joint log-likelihood)：
$$l(\mu ,b)=\log L=-n\log 2b-\frac{1}{b}\sum _i^N\frac{\partial |x_i-\mu |}{\partial \mu }$$
其中需要绝对值求导：
$$\frac{\partial |x|}{\partial x}=\frac{\partial \sqrt{x^2}}{\partial x}=x(x^2{)}^{-1/2}=\frac{x}{|x|}=\mathrm{sgn}(x)$$
对$\mu$求偏导并等于0:
$$\frac{\partial l(\mu ,b)}{\partial \mu }=\frac{1}{b}\sum _{i=1}^N\mathrm{sgn}(x_i-\mu )=0$$
此时的解只与$N$有关。

1. $N$是奇数，显然$\hat{\mu }=\mathrm{median}(x_1,\dots ,x_N)$。因为$\frac{N-1}{2}$个样本小于中位数，为$-1$，$\frac{N-1}{2}$个样本大于中位数，为$+1$。所以满足等式为$0$。
2. $N$是偶数，解为$x_{N/2}$或$x_{(N+1)/2}$。
   另外：
   $$\hat{b}=\frac{1}{N}\sum _{i=1}^N|x_i-\hat{u}|$$

2.3 LAD回归(分位数回归的特例)

考虑一个简单的LAD线性回归问题，包括$N$个观测$(X_i,Y_i)$:
$$Y_i=a{X}_i+b+U_i,i=1,2,\dots ,N$$
其中$a$是直线斜率,$b$是截距项。$U_i$是服从零均值$f(U)=(1/2\lambda )e^{-|U|/\lambda }$的拉普拉斯分布，方差为${\sigma }^2=2{\lambda }^2$。则此时的目标函数为
$$F(a,b)=\sum _{i=1}^N|Y_i-a{X}_i-b|$$
对于如何求解$a,b$有如下算法。先建立一个线性回归模型，其中固定$a=a_0$:
$$F(b)=\sum _{i=1}^N|Y_i-a_0{X}_i-b|$$
对于之前设定的误差项$U_i$，$b$的解是极大似然估计量
$$b^{\ast }=\mathrm{med}(Y_i-a_0{X}_i{|}_{i=1}^N)$$
另一方面，如果固定$b=b_0$，目标函数为:
$$\begin{array}{rl}F(a)& =\sum _{i=1}^N|Y_i-b_0-a{X}_i|\\ & =\sum _{i=1}^N|X_i|\left|\frac{Y_i-b_0}{X_i}-a\right|\end{array}$$
由于随机误差项是拉普拉斯分布的，$\{(Y_i-b_0)/X_i\}$也是拉普拉斯分布的，此时$a$的解是
$$a^{\ast }=\mathrm{med}\left(|X_i|△{\frac{Y_i-b_0}{X_i}|}_{i=1}^N\right)$$
其中$△$是复制运算符，对于正整数$|X_i|$, $|X_i|△Y_i$表示$Y_i$被复制|X_i|次，如果$|X_i|$不是整数，计算加权中位数：
$$Y=\mathrm{med}\left({W_i△X_i|}_{i=1}^N\right)$$
算法如下:

1. 计算阈值$W_0=(1/2){\sum }_{i=1}^N{W}_i$
2. 对样本排序$X_{(1)},\dots ,X_{(N)}$并伴随相应的权重$W_{[1]},\dots ,W_{[N]}$
3. 按顺序将$W_{[1]}$向上求和
4. 第一个满足${\sum }_{i=1}^j{W}_{[i]}>W_0$的$X_{(j)}$就是加权中位数$Y$

由此可以得到贪婪坐标下降算法的步骤：
(1). 令$k=0$，设定初值$a_0$
(2). 令$k=k+1$, 用$a_{k-1}$获得$b$的估计
$$b_k=\mathrm{med}\left({Y_i-a_{k-1}{X}_i|}_{i=1}^N\right)$$
(3). 利用$b_k$获得$a$的第$k$次估计：
$$a_k=\mathrm{med}\left(|X_i|△{\frac{Y_i-b_k}{X_i}|}_{i=1}^N\right)$$
(4). 当$a_k-a_{k-1}$和$b_k-b_{k-1}$在允许误差范围时停止迭代，否则返回(2).

2.4 Python实现

data = pd.read_csv(r"C:\Users\beida\Desktop\sc\rent.csv")
n = len(data); p = 1
x = np.insert(np.matrix(data["area"],dtype=np.float64).reshape((n, p)), obj=0, values=np.ones(n), axis=1)
#x = np.matrix(data["area"][0:n]).reshape((n, 1))
y = np.matrix(data["rent_euro"],dtype=np.float64).reshape(n, 1)
#beta = np.matrix([100, 2.6]).reshape(p, 1)

我们还是使用第一章的数据，并且进行中位数回归

#np.set_printoptions(precision=8)
tau = 0.5
maxit = 100
toler = 0.0001
error = 10000
iteration = 1
p = 1
#beta = np.matrix([1, 1], dtype=np.float64).reshape(2, 1)
beta = np.linalg.pinv(x.T.dot(x)).dot(x.T).dot(y)
#print(beta, "ols")
while (iteration <= maxit) & (error>toler):
    betaold = beta.copy()
    #print(betaold, 'betaold')
    uv = np.sort(y-x.dot(beta), axis = 0) #yes
    quantile1 = (n-1)*tau - np.floor((n-1)*tau) #yes
    #quantile2 = 1 - tau
    #int(np.ceil((n-1)*tau)), int(np.floor((n-1)*tau))
    #uv[80]*0.2 + uv[80]*0.8 
    u = quantile1*uv[int(np.ceil((n-1)*tau))] \
        + (1-quantile1)*uv[int(np.floor((n-1)*tau))] #yes
    r = y - u - x.dot(beta) #yes
    signw = (1 - np.sign(r))/2*(1-tau) + (np.sign(r)+1)*tau/2 #yes
    for j in range(0, p+1):
        z = (r + x[:,j]*beta[j])/x[:, j] #yes
        order = z.A[:,0].argsort() #yes
        sortz = z.A[order] #yes
        newX = np.multiply(x[:,j], signw) #
        newX = newX.astype('float64')
        w = np.abs(newX[order]) #
        index = np.where(np.cumsum(w) > (np.sum(w)/2))[1][0] #YES
        beta[j] = sortz[index][0] #
        #print(betaold, "betaold")
    error = np.sum(np.abs(beta-betaold))
    iteration = iteration + 1
print(beta)

按照算法编写代码，结果为：

> [[135.63724592]
   [  4.21550906]]

显然这和之前的线性规划、rq函数存在着差异，其中截距项差距较大，斜率差距仅为0.018. 可见坐标下降算法的优势在于计算速度较快(显著快于线性规划)，但需要精度作为代价。

参考文献

• [1] Wu, T. T., & Lange, K. (2008). Coordinate descent algorithms for lasso penalized regression. The Annals of Applied Statistics, 2(1), 224-244.

---

3 IRWS(迭代重加权最小二乘)

求解分位数回归的另一个算法是迭代重加权最小二乘(Iteratively Reweighted Least Squares, IRLS). 也有学者称之为迭代加权最小二乘(Iteratively Weighted Least Squares, IWLS), 虽然它们最后指向同一个算法，但是实际上IWLS这个说法不准确，因为每次迭代过程中的权重矩阵是不相同，相当于每次重新进行了加权，所以称之为重加权(Reweighted)。
这个算法的适用范围较广，表达较为清晰简洁。

3.1 考虑一个${\ell }_p$线性回归

寻找参数$\mathbf{\beta }=({\beta }_1,\dots ,{\beta }_k{)}^{\top }$来最小化：
$$\underset{\mathbf{\beta }}{\mathrm{argmin}}||\mathbf{y}-\mathbf{X}\mathbf{\beta }|{|}_p=\underset{{\beta }_1,\dots ,{\beta }_k}{\mathrm{argmin}}\sum _{i=1}^n|y_i-X_i\mathbf{\beta }{|}^p$$
对于第$t+1$次迭代，IRLS算法求解的是一个加权最小二乘问题
$$\begin{array}{rl}{\mathbf{\beta }}^{(t+1)}& =\underset{\mathbf{\beta }}{\mathrm{argmin}}\sum _{i=1}^n{w}_i^{(t)}|y_i-X_i{\mathbf{\beta }}^{(t)}{|}^2\\ & =({\mathbf{X}}^{\top }{\mathbf{W}}^{(t)}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\top }{\mathbf{W}}^{(t)}\mathbf{y}\end{array}$$
其中$W^{(t)}$是由权重组成的对角阵，初始值为
$$w_0^{(0)}=1$$
下次更新值
$$w_i^{(t)}=|y_i-{\mathbf{X}}_i{\mathbf{\beta }}^{(t)}{|}^{p-2}$$
显然当$p=1$时就是LAD回归
$$w_i^{(t)}=\frac{1}{\left|y_i-X_i{\mathbf{\beta }}^{(t)}\right|}$$
为了避免分母为0：
$$w_i^{(t)}=\frac{1}{\max \left\{\delta ,\left|y_i-X_i{\mathbf{\beta }}^{(t)}\right|\right\}}$$
其中$\delta$是一个非常小的数。这个符号与稳健回归(Robust)中的Huber Loss Function中的$\delta$是相同的。

3.2 Python实现

还是相同的数据集

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from tqdm.autonotebook import tqdm


data = pd.read_csv(r"C:\Users\beida\Desktop\sc\rent.csv")
X = np.array(data['area']) #解释变量 
Y = np.array(data['rent_euro']) #响应变量

nobs = len(X) 样本量
constant = np.ones(nobs) #截距项列
X = np.column_stack((constant, X))  #设计阵
W = np.diag([1] * len(X)) #权重矩阵初始化

同样采用中位数回归

q = 0.5
for i in tqdm(range(100), colour='blue'):
    beta = np.dot(np.dot(np.dot(np.linalg.inv(np.dot(np.dot(X.T, W), X)), X.T), W), Y)
    resid = Y - np.dot(X, beta)
    resid = np.where(resid < 0, q * resid, (1-q) * resid)
    resid = np.abs(resid)
    W = np.diag(1/resid)
    
print(beta)

由于目的是为了测试算法，所以直接使用了for循环，结果如下

statsmodels库也提供了分位数回归的接口

mod = smf.quantreg("rent_euro ~ area", data)
res = mod.fit(q=0.5)
print(res.summary())

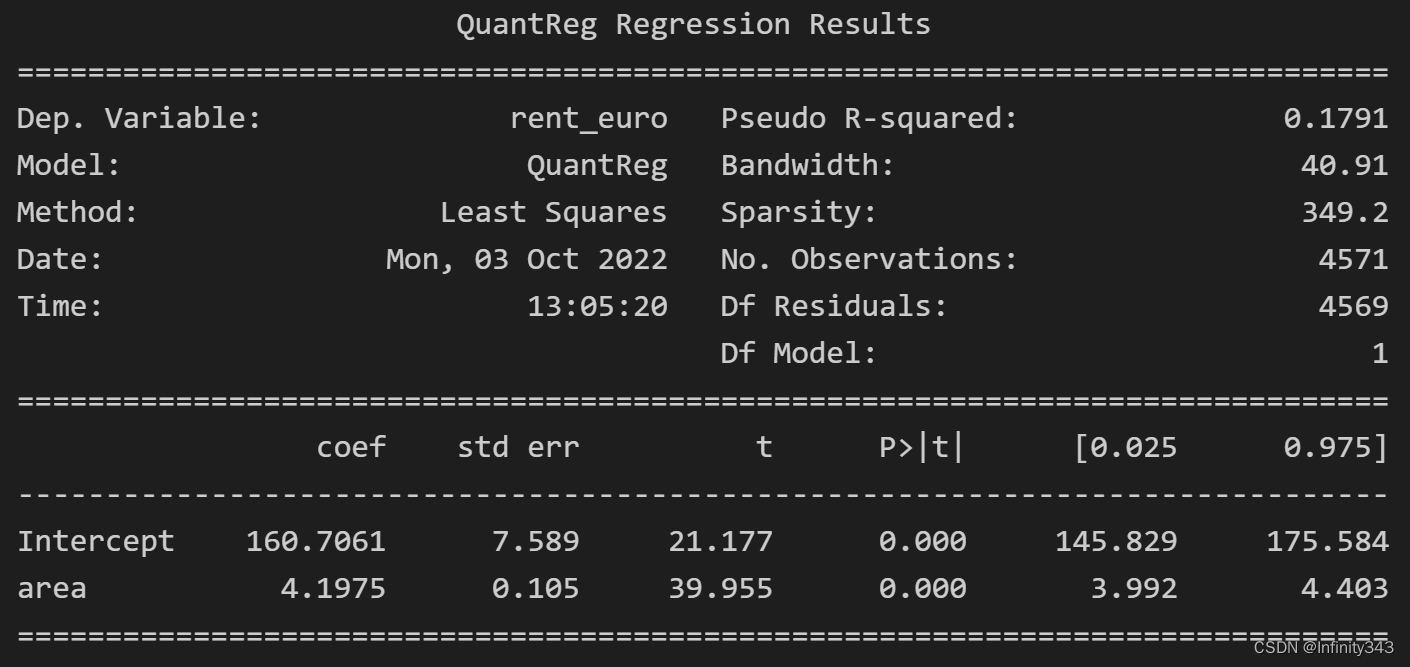
可见结果是完全相同的。

与R的结果也相同。

参考文献

• [1] Lejeune, M. G., & Sarda, P. (1988). Quantile regression: a nonparametric approach. Computational Statistics & Data Analysis, 6(3), 229-239.

---

4 MM算法

4.1 介绍

MM 算法是一种迭代优化方法，它利用函数的凸性来找到它的最大值或最小值。 MM 代表“Majorize-Minimization”或“Minorize-Maximization”，具体取决于所需的优化是最小化还是最大化。 尽管有这个名字，MM 本身并不是一个算法，而是描述了如何构造一个优化算法。

期望最大化算法（EM algorithm）可以被视为 MM 算法的一个特例。 但是，在EM算法中通常会涉及到条件期望，而在MM算法中，凸性和不等式是主要关注点，在大多数情况下更容易理解和应用。

MM 算法的工作原理是找到一个使目标函数最小化或重大化的替代函数。优化替代函数(surrogate function)要么提高目标函数的值，要么保持不变。取minorize-maximization 版本，令$f(\theta )$ 为要最大化的目标凹函数。在算法的$m$步骤，$m=0,1\dots$，构造函数$g\left(\theta \mid {\theta }_m\right)$将被称为目标函数的小化版本（代理函数）在 ${\theta }_m$ if
$$\begin{array}{rl}& g\left(\theta \mid {\theta }_m\right)\le f(\theta )\text{ for all }\theta \\ & g\left({\theta }_m\mid {\theta }_m\right)=f\left({\theta }_m\right)\end{array}$$
然后，最大化 $g\left(\theta \mid {\theta }_m\right)$ 而不是 $f(\theta )$，并让
$${\theta }_{m+1}=\arg \underset{\theta }{\max }g\left(\theta \mid {\theta }_m\right)$$
上述迭代方法将保证 $f\left({\theta }_m\right)$ 在 $m$ 趋于无穷大时收敛到局部最优值或鞍点。由上述构造
$$f\left({\theta }_{m+1}\right)\ge g\left({\theta }_{m+1}\mid {\theta }_m\right)\ge g\left({\theta }_m\mid {\theta }_m\right)=f\left({\theta }_m\right)$$
${\theta }_m$ 和替代函数相对于目标函数的行进如图所示。 Majorize-Minimization 是相同的过程，但具有要最小化的凸目标。由于我们的重点是使用该算法来求解分位数回归，所以不对MM算法做过多解释。

4.2 分位回归中的MM算法

对于一个$p$维的分位回归问题，我们需要最小化以下损失函数：
$$L(\theta )=\sum _{i=1}^n{\rho }_q[y_i-f_i(\theta )]$$
为了简化记号，将第$i$个残差定义为$r_i(\theta )=y_i-f_i(\theta )$,通常记为$r_i$而忽略参数$\theta$, 另外$x_i$是协变量$X_{n\times p}$的第$i$行，这样：$f_i\theta )=x_i\theta$. 需要假定每个$f_i(\theta ):R^p\to R$拥有连续导数$d{f}_i(\theta )$, 我们的目标是用更简化的函数来逼近${\rho }_q(r)$，为此定义$ϵ>0$:
$${\rho }_q^{ϵ}(r)={\rho }_q(r)-\frac{ϵ}{2}(\ln ϵ+|r|)$$
逐项求和
$$L_{ϵ}(\theta )=\sum _{i=1}^n{\rho }_q^{ϵ}(r_i)$$
用上式来逼近$L(\theta )$, 这表明对于给定第$k$次迭代的残差$r^k=r({\theta }^k)$，${\rho }_q^{ϵ}(r)$由以下二次函数来优化
$${\zeta }_q^{ϵ}\left(r\mid r^k\right)=\frac{1}{4}\left[\frac{(r{)}^2}{ϵ+\left|r^k\right|}+(4q-2)r+c\right]$$
$c$是一个常数使得${\zeta }_q^{ϵ}(r^k|r^k)={\rho }_q^{ϵ}(r^k)$. 有了简化后的优化函数，MM算法的目标就变成了最小化这个相对简单的函数
$$Q_{ϵ}\left(\theta \mid {\theta }^k\right)=\sum _{i=1}^n{\zeta }_q^{ϵ}\left(r_i\mid r_i^k\right)$$
虽然我们目前研究的是线性分位数回归，但实际情况中$f_i(\theta )$很难保证是线性的，对于线性的情况，最小化这个目标函数可以使用牛顿法，但是牛顿法需要Hessian矩阵正定，另一方面，$f_i(\theta )$的二阶导数计算起来非常麻烦，而且一旦$f_i(\theta )$非线性就无法计算了，所以采取了Gauss-Newton迭代(可以处理非线性回归，但只能处理二次函数，而目标函数又刚好是二次的，相比较牛顿法又抛弃了二阶导数项，所以好计算)
一阶导数
$$\begin{array}{rl}\frac{d{Q}_{ϵ}(\theta |{\theta }^k)}{d\theta }& =\frac{1}{2}\sum _{i=1}^n\left[\frac{r_i}{ϵ+|r_r^k|}+2q-1\right]d{r}_i(\theta )\\ & =\frac{1}{2}{v}_{ϵ}(\theta )df(\theta )\end{array}$$
其中
$$v_{ϵ}(\theta )=\left(1-2q-\frac{r_1(\theta )}{ϵ+\left|r_1(\theta )\right|},\dots ,1-2q-\frac{r_n(\theta )}{ϵ+\left|r_n(\theta )\right|}\right)$$
二阶导数
$$\begin{array}{rl}\frac{d^2{Q}_{ϵ}(\theta |{\theta }^k)}{d{\theta }^2}& \approx \frac{1}{2}\sum _{i=1}^n\frac{1}{ϵ+|r_i^k|}d{r}_i(\theta {)}^{\top }d{r}_i(\theta )\end{array}$$
由于$d{r}_i(\theta )=-d{f}_i(\theta )$所以当$f_i(\theta )$是线性的时候这个逼近是精确的。可以将上式改写为更简便的形式：
$$d^2{Q}_{ϵ}\left(\theta \mid {\theta }^k\right)\approx \frac{1}{2}df(\theta {)}^t{W}_{ϵ}\left({\theta }^k\right)df(\theta )$$
这个时候GN迭代的方向就是
$${\Delta }_{ϵ}^k=-{\left[df{\left({\theta }^k\right)}^t{W}_{ϵ}\left({\theta }^k\right)df\left({\theta }^k\right)\right]}^{-1}df{\left({\theta }^k\right)}^t{v}_{ϵ}{\left({\theta }^k\right)}^t$$
其实这个形式在一维的时候就是:
$${\beta }^{k+1}={\beta }^k-\frac{f^{\prime }(x)}{f^{\prime \prime }(x)}$$
特别的，当进行线性回归的时候$f_i(\theta )=x_i\theta$，$df(\theta )=X$,此时迭代公式${\theta }^{k+1}={\theta }^k+{\Delta }_{ϵ}^k$就是求解$d{Q}_{ϵ}(\theta |{\theta }^k)=0$.

4.3 Python实现

还是使用相同的数据集和设定

data = pd.read_csv("//JOHNWICK/Users/beida/Desktop/sc/rent.csv")
n = len(data); p = 1
x = np.array(data[["cons", 'area']])

y = np.array(data["rent_euro"], dtype=np.float64)
beta = np.array([100, 2.6])

n = x.shape[0]
p = x.shape[1]
xt = x.T
iteration = 1
product = np.ones((p, n))

tau = 0.5
error = 10000
epsilon = 0.9999
maxit = 100
toler = 1e-3
while (iteration <= maxit) & (error > toler):
    betaold = beta
    r = y - x.dot(beta)
    v = 1 - 2*tau - r / (np.abs(r)+epsilon)
    w = 1/(epsilon+np.abs(r))

    for i in range(0, n):
        product[:,i] = xt[:,i]*w[i]
        
    delta = np.linalg.solve(product.dot(x), xt.dot(v))
    beta  = beta - delta
    iteration += 1
    error = np.sum(np.abs(delta))
    
beta

结果

> array([160.3660159 ,   4.19819691])

结果对比

可以看到估计结果仅在截距项上存在着细微的差距。

参考文献

• [1] Hunter, D. R., & Lange, K. (2004). A tutorial on MM algorithms. The American Statistician, 58(1), 30-37.
• [2] Hunter, D. R., & Lange, K. (2000). Quantile regression via an MM algorithm. Journal of Computational and Graphical Statistics, 9(1), 60-77.
• [3] Lange, K., Chambers, J., & Eddy, W. (1999). Numerical analysis for statisticians (Vol. 2). New York: Springer.

5 ADMM算法

交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)。由于该算法的内容较多且稍微复杂一些(需要一些凸优化方面的数学基础知识)，所以我们直接介绍如何使用该算法来求解QR

5.1 求解LAD

对于LAD问题，我们之前已经证明了它可以写为一个线性规划的形式
$$\begin{gathered} \mathrm{minimize}||z|{|}_1 \\ s.t.Ax-b=z \end{gathered}$$
将上述规划写为增广拉格朗日形式(Augmented Lagrangian form):
$$L(x,y,z)=\Vert z{\Vert }_1+y^T(Ax-b-z)+\rho /2\Vert Ax-b-z{\Vert }_2^2$$
将$y$组合到$l_2$正则项中
$$L(x,y,z)=\Vert z{\Vert }_1+\rho /2\Vert Ax-b-z+(y/\rho ){\Vert }_2^2$$
用 $u$ 来替换$y/\rho$
$$L(x,y,z)=\Vert z{\Vert }_1+\rho /2\Vert Ax-b-z+u{\Vert }_2^2$$
为了更新$x$，我们假定$z^k$和$u^k$已知
$$\begin{gathered} x^{k+1}=\underset{x}{\mathrm{argmin}}{L}_p\left(x,z^k,u^k\right) \\ {x}^{k+1}=\underset{x}{\arg \min 1/2}{\Vert Ax-b-z^k+u^k\Vert }_2^2 \end{gathered}$$
计算一阶偏导数并令其等于零，来获得$x^{(k+1)}$
$$\begin{array}{rl}& \frac{\delta L\left(x^{k+1},z,u^k\right)}{\delta z}=2A^T\left(Ax-b-z^k-u^k\right)=0\\ & x^{k+1}={\left(A^{T}A\right)}^{-1}{A}^T\left(b+z^k-u^k\right)\end{array}$$
类似的也可以更新$z$
$$z^{k+1}=\arg \underset{z}{\min }{L}_p\left(x^{k+1},z,u^k\right)$$
考虑和$z$相关的项
$$z^{k+1}=\underset{z}{\mathrm{argmin}}\Vert z{\Vert }_1+(\rho /2){\Vert A{x}^{k+1}-b-z+u^k\Vert }_2^2$$
将 $\rho$带入公分母常数，进行一下变换
$$z^{k+1}=\underset{z}{\mathrm{argmin}}\Vert z{\Vert }_1+(1/(2/\rho )){\Vert A{x}^{k+1}-b-z+u^k\Vert }_2^2$$

考虑变量$v$上的近端算子，其中某个常数 α 定义为，
$${\mathrm{prox}}_f(v)=\arg \min \left(f(x)+1/2\alpha \Vert x-v{\Vert }_2^2\right)\equiv S_{\alpha }(v)$$
这样${\mathrm{z}}^{(k+1)}$就有一个更加紧凑的形式
$$z^{k+1}=S_{(1/\rho )}\left(A{x}^{k+1}-b+u^k\right)$$
由于$x^{(k+1)}$和$z^{(k+1)}$都有了，这样就可以更新$u$
$$u^{k+1}=u^k+\left(A{x}^{k+1}-b-z^{k+1}\right)$$
综上所述
$$\begin{array}{r}{x}^{k+1}={\left(A^{T}A\right)}^{-1}{A}^T\left(b+z^k-u^k\right)\\ z^{k+1}=S_{(1/\rho )}\left(A{x}^{k+1}-b+u^k\right)\\ u^{k+1}=u^k+\left(A{x}^{k+1}-b-z^{k+1}\right)\end{array}$$

5.2 Python实现

还是相同的设定

data = pd.read_csv(r"D:\Desktop\RUC\第一学期\课程\统计计算\rent.csv")
n = len(data); p = 1
x = np.array(data[["cons", 'area']])

y = np.array(data["rent_euro"], dtype=np.float64)
#beta = np.matrix([100, 2.6]).reshape(p, 1)

A = xx  # A is data
m, n = xx.shape
b = y
rho = 1
iteration = 1
maxit = 5000
x = np.zeros(n)
z = np.zeros(m)
u = np.zeros(m)
P = np.linalg.inv(A.T.dot(A)).dot(A.T)
tau = 0.9
toler = 1e-5
error = 10000


def shrinkage(x, kappa):
    z = np.maximum(0, x - kappa) - np.maximum(0, -x - kappa)
    w = np.multiply((1+np.sign(x - kappa))/2, (x - kappa)) - \
        np.multiply((1+np.sign(-x - kappa))/2, (-u - v))
    return z

    # P = (A'A)^-1A'
while (iteration <= maxit) & (error > toler):
    xold = x
    x = P.dot(b + z - u)

    e = A.dot(x)
    # b is y, e is Ax, u is m×1 matrix
    z = shrinkage(x=(e - b + u/rho + (2*tau - 1)/rho), kappa=(1/rho))
    u = u + (e - z - b)
    
    error = np.sum(np.abs(x - xold))
    iteration += 1

x

> array([121.83857468,   7.86501805])

还是与rq函数进行比较

在我们提高了精度后结果基本一致。

参考文献

• Boyd, S., Parikh, N., Chu, E., Peleato, B., & Eckstein, J. (2011). Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends® in Machine learning, 3(1), 1-122.
• tip: Boyd是来自斯坦福大学的教授，是ADMM这方面的大佬

6 BR算法

7 内点算法(高计算、内存性能时代的最佳选择)