计算机算法设计与分析——复习题

最新推荐文章于 2022-10-03 21:48:36 发布

可一z可再

最新推荐文章于 2022-10-03 21:48:36 发布

阅读量2k

点赞数 2

分类专栏：计算机算法设计与分析

本文链接：https://blog.csdn.net/qq_44691784/article/details/103549070

版权

计算机算法设计与分析专栏收录该内容

8 篇文章 0 订阅

订阅专栏

1.快速排序

例题：对数组A={15，29，135，18，32，1，27，25，5}，用快速排序方法将其排成递增序列。简要回答快速排序的思想和上述数组的排序过程。
基本思想
　　在待排序的n个元素中任取一个元素（通常取第一个元素）作为基准，把该元素放入最终位置后，整个数据序列被基准分割成两个子序列，所有小于基准的元素放置在前子序列中，所有大于基准的元素放置在后子序列中，并把基准排在这两个子序列的中间，这个过程称作划分。
　　然后对两个子序列分别重复上述过程，直至每个子序列内只有一个记录或空为止。
　　注：每一次划分时，先从后向前找（j.key<key），再从前向后找(i.key>key),直到i=j。

快速排序算法

int Partition(int a[],int s.int t)//划分算法
{
	int i=s,j=t;
	int tmp=a[s];//用序列的第1个记录作为基准
	while(i!=j)//用序列两端交替向中间扫描，直至i=j为止
	{
		while(j>1&&a[j]>=tmp)
			j--;//从右向左扫描，找第1个关键字小于tmp的a[j]
		a[i]=a[j];//讲a[j]前移到a[i]的位置
		while(i<j&&a[i]<=tmp)
			i++;//从左向右扫描，找第1个关键字大于tmp的a[i]
		a[j]=a[i];
	}
	a[i]=tmp;
	return i;
}
void QuickSort(int a[],int s,int t)//对a[s..t]元素序列进行递增排序
{
	if(s<t)//序列内至少存在2个元素的情况
		{
			int i=Partition(a,s,t);
			QuickSort(a,s,i-1);//对左子序列递归排序
			QuickSort(a,i+1,t);//对右子序列递归排序
		}
}

2.折半查找

例题：使用折半查找算法对A=｛1，5，15，18，25，27，29，32，135｝所得到的结果搜索如下元素，并给出搜索过程：18，31
基本思想
　　设a[low…high]是当前的查找区间，首先确定该区间的中点位置mid=(low+high)/2；然后将待查的k值与a[mid].key比较：
（1）若k==a[mid]，则查找成功并返回该元素的物理下标；
（2）若k<a[mid]，则由表的有序性可知a[mid+1…high]均大于k，因此若表中存在关键字等于k的元素，则该元素必定位于左子表a[low…mid-1]中，故新的查找区间是左子表a[low…mid-1]；
（3）若k>a[mid]，则要查找的k必在位于右子表a[mid+1…high]中，即新的查找区间是右子表a[mid+1…high]。
　　下一次查找是针对新的查找区间进行的。
折半查找算法

int BinSearch(int a[],int low,int high,int k)//折半查找算法
{
	int mid;
	if(low<=high)//当前区间存在元素时
	{
		mid=(low+high)/2;//求查找区间的中间位置
		if (a[mid]==k)//找到后返回其物理下标mid
			return mid;
		if(a[mid]>k)//当a[mid]>k时
			return BinSearch(a,low,mid-1,k);
		else
			return BinSearch(a,mid+1,high,k);
	}
	else return -1;//若当前查找区间没有元素时返回-1
}

3.动态规划

例题：用动态规划法求最大子段的问题，求序列（-20，11，-4，13，-5，-2）的最大子段，并写出求解过程。
基本思想
　　将待求解问题分解成若干子问题，先求解子问题，再结合这些子问题的解得到原问题的解。每次决策依赖于当前状态，又随即引起状态的转移。一个决策序列就是在变化的状态中产生出来的，所以，这种多阶段最优化决策解决问题的过程就称为动态规划。
最大子段和算法

int n=6;
int a[]={-20，11，-4，13，-5，-2};//a数组不用下标为0的元素
int dp[MAXN];
void maxSubSum()//求dp数组
{
	dp[0]=0;
	for(int j=1;j<=n;j++)
		dp[j]=max(dp[j-1]+a[j],a[j]);
}
void dispmaxSum()//输出结果
{
	int maxj=1;
	for(int j=2;j<=n;j++)//求dp中最大元素dp[maxj]
		if(dp[j]>dp[maxj])
			maxj=j;
	for(int k=maxj;k>=1;k--)//找前一个值小于等于0的元素
		if(dp[k]<=0)
			break;
			printf("最大连续子序列和：%d\n",dp[maxj]);
	print("所选子序列：");
	for(int i=k+1;i<=maxj;i++)
		print("%d",a[i]);
	print("\n");
}

//简单的算法
int n=6;
int a[]={-20，11，-4，13，-5，-2};
int MaxSum(int n,int a[])
{
	int sum=0,x=0;
	for(int i=1;i<=n;i++)
	{
		if(x>0)
			x+=a[i];
		else
			x=a[i];
		if(x>sum)
			sum=x;
	}
	return sum;
}

4.递归算法

例题：执行完下列语句段后，
int f(int x)
{return ((x>0)?x*f(x-1):2;}
int i;
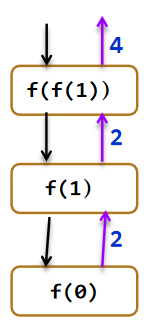
i=f(f(1));
（1）请问i值为多少。
（2）并简要分析该算法执行过程。
基本思想
　　递归调用的实现是分两步进行的，第一步是分解过程，即用递归体将“大问题”分解成“小问题”，直到递归出口为止，然后进行第二步的求值过程，即已知“小问题”，计算“大问题”。
在这里插入图片描述

5.贪心法

例题：设某通信电文有a,b,c,d,e五个字符组成，它们在电文中出现的次数分别为14，7，10，3，21。给出他们的huffuman编码，画出对应的huffuman树，并解释其所用的算法类型。
基本思想
　　贪心算法通过一系列选择来得到问题的解，所做的每个选择都是当前状态下局部最好选择，即贪心选择。贪心法在解决问题的策略上目光短浅，只根据当前已有的信息就做出选择，而且一旦做出选择，不管将来有什么结果，这个选择都不会改变。换言之，贪心法并不是从整体最优考虑。
哈夫曼树
在这里插入图片描述

6.棋盘覆盖问题

例题：请给出n×n棋盘覆盖问题的算法分析，并写出伪代码或代码描述。
【问题求解】棋盘中的方格数=2^k× 2^k=4^k，覆盖使用的L型骨牌个数=（4^k-1）/3。
采用的方法是：将棋盘划分为4个大小相同4个象限，根据特殊方格的位置（dr,dc），在中间位置放置一个合适的L型骨牌。
思路分析
(1)把棋盘等分成四个正方形分别是：左上、左下、右上、右下四个子棋盘。
(2)对于每一个子棋盘，如果其存在特殊方格，将它再分成四个子棋盘，并且使用同样的方法，对子棋盘进行递归。
(3)对于不存在特殊方格的子棋盘，假定与另外三个子棋盘相接的为特殊方格（用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处），有了特殊方格之后，对这个子棋盘进行递归
(4)直到子棋盘为1*1的正方形。
例如，如下图所示，特殊方格在左上角象限中，在中间放置一个覆盖其他3个象限中各一个方格的L型骨牌。
在这里插入图片描述

　　用（tr，tc）表示一个象限左上角方格的坐标，（dr，dc）是特殊方格所在的坐标，size是棋盘的行数和列数。
　　用二维数组board存放覆盖方案，用tile全局变量表示L型骨牌的编号（从整数1开始），board中3个相同的整数表示一个L型骨牌。
　在这里插入图片描述

#include<stdio.h>
#define MAX 1025
//问题表示
int k;				//棋盘大小
int x,y;			//特殊方格的位置
//求解问题表示
int board[MAX][MAX];
int tile=1;	

void ChessBoard(int tr,int tc,int dr,int dc,int size)
{   if(size==1) return;		//递归出口
    int t=tile++;			//取一个L型骨，其牌号为tile
    int s=size/2;			//分割棋盘
    
    //考虑左上角象限
    if(dr<tr+s && dc<tc+s)		//特殊方格在此象限中
	ChessBoard(tr,tc,dr,dc,s);
    else				//此象限中无特殊方格
    {	board[tr+s-1][tc+s-1]=t;	//用t号L型骨牌覆盖右下角
	ChessBoard(tr,tc,tr+s-1,tc+s-1,s);	
				//将右下角作为特殊方格继续处理该象限
    }

    //考虑右上角象限
    if(dr<tr+s && dc>=tc+s)  
	ChessBoard(tr,tc+s,dr,dc,s);		//特殊方格在此象限中 
    else					//此象限中无特殊方格
    {	board[tr+s-1][tc+s]=t;		//用t号L型骨牌覆盖左下角
	ChessBoard(tr,tc+s,tr+s-1,tc+s,s);  	
				//将左下角作为特殊方格继续处理该象限
    }

    //处理左下角象限
    if(dr>=tr+s && dc<tc+s)		//特殊方格在此象限中
	ChessBoard(tr+s,tc,dr,dc,s);  
    else				//此象限中无特殊方格
    {   board[tr+s][tc+s-1]=t;  	//用t号L型骨牌覆盖右上角
        ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
				//将右上角作为特殊方格继续处理该象限
    }
    
	//处理右下角象限
    if(dr>=tr+s && dc>=tc+s)		//特殊方格在此象限中
        ChessBoard(tr+s,tc+s,dr,dc,s); 
    else				//此象限中无特殊方格
    {	board[tr+s][tc+s]=t;  	//用t号L型骨牌覆盖左上角
	ChessBoard(tr+s,tc+s,tr+s,tc+s,s);  	
				//将左上角作为特殊方格继续处理该象限
    }
}

8.求解旅行商问题（TSP问题）

例题：某市场营销人员从他所在城市(项点1)出发，到其他5个城市去做市场调查，如下图所示。请设计行走路线。
在这里插入图片描述
基本思路
（动态规划求解）
　　假设从顶点s出发，令d(i, V)表示从顶点i出发经过V(是一个点的集合)中各个顶点一次且仅一次，最后回到出发点s的最短路径长度。
①当V为空集，那么d(i, V)，表示从i不经过任何点就回到s了。
　　d(i, V)=Cis(城市i 到城市s 的距离)
②如果V不为空，那么就是对子问题的最优求解。你必须在V这个城市集合中，尝试每一个，并求出最优解。
　　d(i, V)=min{Cik（选择的城市k 和城市i 的距离） + d(k, V-{k})（下一个子问题）}

1.将顶点1存入路径列表
2.从顶点1出发，找出所有的可到达的点，将可到达点和对应距离存入路径列表中
3.将路径列表中的每一个已到达顶点重新作为起点，找出每一个起点的所有的可到达的点，排除路径记录中已走过的点，将剩下的可到达点和对应累加后的距离，存入到路径列表中
4.重复操作2，一直到路径记录中包含所有的点
5.从所有记录中挑出总路径最短的路径记录作为本次行走的路线

过程：
①
d(1,{2,5,6})=min{
　　　　　　　8+d(2,{3,4,6})；
　　　　　　　9+d(5,{4,6})；
　　　　　　　1+d(6,{2,4,5})；
　　　　　　　}
②
d(2,{3,4,6})=min{
　　　　　　5+d(3,{4})；
　　　　　　7+d(4,{3,5,6});
　　　　　　4+d(6,{4,5};
　　　　　　}
d(5,{4,6})=min{　
　　　　　　3+d(6,{2,4})；
　　　　　　6+d(4,{2,3,6})；
　　　　　　}
d(6,{2,4,5})=min{　
　　　　　　4+d(2,{3,4})；
　　　　　　7+d(4,{2,3})；
　　　　　　3+d(5,{4});
　　　　　　}　
③
…
按照上面的思路，只有最后一层的，当V为空集时，Cis的值才可以求。

（贪心法求解）
　　实际上TSP问题不满足贪心法的最优子结构性质，所以采用贪心法不一定得到最优解，但可以采用合理的贪心策略。
　　如可以采用最近邻点策略，即从任意城市出发，每次在没有到过的城市中选择最近的一个，直到经过了所有的城市，最后回到出发城市。
　　
过程：
min{ d(1,V(2,5,6)）}=1——>
mid{ d(6,V(2,4,5)）}=3——>
mid{ d(5,V(4)）}=6——>
mid{ d(4,V(2,3)）}=7——>
mid{ d(2,V(3)）}=5
mid=1+3+6+7+5=22

9.求算法复杂度

x=1;
for(i=1;i<=n;i++)
	for(j=1;j<=i;j++)
		for(k=1;k<=j;k++)
			x++;

i=1;
while i<n
	do
	i=i*3

解：
1.
$\sum_{i=1}^{n}$ $\sum_{j=1}^{i}$ $\sum_{k=1}^{j}1$ = $\sum_{i=1}^{n}$ $\sum_{j=1}^{i}j$ = $\sum_{i=1}^{n}i(i+1)/2$ =[n(n+1)(2n+1)/6+n(n+1)/2]/2=n(n+1)(n+2)/6
O(n)=n³
2.
因为i=1,3,9,27…=3^x
所以3^x<n　==>　x<= log3ⁿ
O(n)=log3ⁿ

10.分析解释经典的冒泡排序算法，尝试从2个角度改进算法，简述改进思路

首先从数组的第一个元素开始到数组最后一个元素为止，对数组中相邻的两个元素进行比较，如果位于数组左端的元素大于数组右端的元素，则交换这两个元素在数组中的位置，此时数组最右端的元素即为该数组中所有元素的最大值。接着对该数组剩下的n-1个元素进行冒泡排序，直到整个数组有序排列。
f(a,n,i)=不做任何事情，算法结束　　　　　　　　　　　当i=n-1
f(a,n,i)=对a[i…n-1]元素序列，从a[n-1]开始
　　　　进行相邻元素比较；　　　　　　　　　　　　　否则
　　　　若相邻两元素反序则将两者交换；
　　　　若没有交换则返回，否则执行f(a,n,i+1);

改进思路：
①传统的冒泡排序中每一趟排序只能找到一个最大值或最小值，效率低，基于这个缺点我们考虑利用在每一趟排序中进行正向和反向俩遍冒泡的方法一次可以得到俩个最终值（最大值和最小值），确定两个值的位置，从而使排序趟数减少了一半。
②传统的冒泡排序中部分数据的顺序排好之后，仍然会继续进行下一轮的比较，直到n-1次，后面的比较是没有意义的。基于这个缺点我们考虑设置标志位flag，如果发生了交换flag设置为true；如果没有交换就设置为false。当一轮比较结束后如果flag仍为false，即：这一轮没有发生交换，说明数据的顺序已经排好，没有必要继续进行下去。

11.分析最简单的串匹配算法（BF算法），简述如何改进BF算法。

基本思路：
1.从目标串S = "s0 s1…s n-1"的第一个字符开始和模式串T = "t0 t1…t m-1"中的第一个字符比较，若相等，则继续逐个比较后续字符；否则从目标串的第二个字符开始重新与模式串t的第一个字符进行比较。
2.依次类推，若从目标串S的第i个字符开始，每个字符依次和模式串T中的对应字符相等，则匹配成功，该算法返回i；否则，匹配失败，函数返回-1。
该算法最坏情况下要进行m*(n-m+1)次比较，时间复杂度为O(m*n)

改进方法：
先将T串的末尾最后一位与S串与之对应的位置进行比较，若发现不同，则后移下一位，若相同，再从T串的第一位开始比较,其算法复杂度为O(m+n)。

12.简述分治递归算法的基本框架，举两个例子说明分治递归算法的实际应用。

分治递归算法
（1）分解，将要解决的问题划分成若干规模较小的同类问题；
（2）求解，当子问题划分得足够小时，用较简单的方法解决；
（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。
实际应用：棋盘覆盖、循环赛日程表、汉诺塔。

蛮力法（穷举法）
（1）确定穷举对象、穷举范围和判定条件；
（2）穷举可能的解，验证是否是问题的解。

分支限界法
（1）求解目标：分支限界法的求解目标则是找出满足约束条件的一个解，或是在满足约束条件的解中找出在某种意义下的最优解。
（2）搜索方式：以广度优先或以最小耗费优先的方式搜索解空间树。分支限界法常以广度优先或以最小耗费（最大效益）优先的方式搜索问题的解空间树。
（3）搜索策略：在分支限界法中，每一个活结点只有一次机会成为扩展结点。活结点一旦成为扩展结点，就一次性产生其所有儿子结点。在这些儿子结点中，导致不可行解或导致非最优解的儿子结点被舍弃，其余儿子结点被加入活结点表中。此后，从活结点表中取下一结点成为当前扩展结点，并重复上述结点扩展过程。这个过程一直持续到找到所需的解或活结点表为空时为止。
实际应用：0-1背包问题、旅行售货员问题

回溯法
把问题的解空间转化成了图或者树的结构表示，然后使用深度优先搜索策略进行遍历，遍历的过程中记录和寻找所有可行解或者最优解。
（1）明确定义问题的解空间，问题的解空间应至少包含问题的一个（最优）解。
（2）确定结点的扩展搜索规则
（3）以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。
实际应用：0-1背包问题、图的m着色问题、旅行售货员问题

贪心法
（1）建立数学模型来描述问题。
（2）把求解的问题分成若干个子问题。
（3）对每一子问题求解，得到子问题的局部最优解。
（4）把子问题的解局部最优解合成原来解问题的一个解。
实际应用：活动安排问题、哈夫曼编码

动态规划
（1）分析最优解的性质，并刻画其结构特征。
（2）递归地定义最优解。
（3）以自底向上的方式计算最优值
（4）根据计算最优值时得到的信息，构造最优解
实际应用：0-1背包问题、旅行售货员问题

13.请设计两种算法求解最长子序列（最大子段和问题），写出伪代码或者程序设计语言并对比分析两种算法的算法设计思路。

最大子段和问题说明：已知序列（-20，11，-4，13，-5，-2），其最长子序列为连续的一段子序列并且这段子序列之和最大。例如，（11，-4，13）为（-20，11，-4，13，-5，-2）的最长子序列。

①穷举法
基本思路：
1.遍历数组，寻找正数：从主串的第一个数字开始，遍历主串，当发现主串的某一位置的值大于0时，将其作为子串的第一个数值，记录当前位置
2.存放子串：继续遍历主串，每扫描主串的一个元素就对其求和，记录存放一个子串
3.重复操作：返回到记录位置+1，继续重复操作1和2，直到整个主串遍历完成
代码：

int sum, maxSum;
sum = 0;
maxSum = 0;
int i, j, k;
for (i = 0; i < n; i++)	{
		for (j = i; j < n; j++){
			sum = 0;
			for (k = i; k <= j; k++)
				sum += a[k];
			if (sum > maxSum)
				maxSum = sum;
		}
	}
return maxSum;

②动态规划法
基本思路：
前面子序列之和
1.大于0,保留sum=sum+a[i]
2.小于等于0，则丢弃，令sum=a[i]
3.记录每一轮的最大长度
代码：

int sum, maxSum;
int i;
sum = 0;
maxSum = 0;
for (i = 0; i < n; i++)	{
	if (sum > 0)
		sum += a[i];
	else 
		sum = a[i];
		
	if(sum >maxSum )
      maxSum =sum ;
	}
return maxSum;

14.0-1背包问题求解

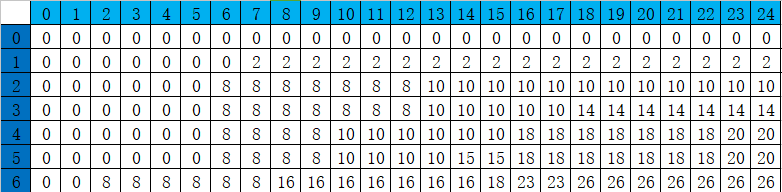
假设有6个物品，它们的重量和价值如下表所示。若这些物品均不能被分割，且背包容量W=120，求出使得物品装入背包不超过背包容量，物品价值最大的方案，使用动态规划方法求解0-1背包问题。

物品	A　　　B　　　C　　　D　　　E　　　F
重量W	35　　30　　60　　50　　40　　10
价值V	10　　40　　30　　50　　35　　40

基本思想：将待求解问题分解成若干个子问题，经分解得到的子问题往往不是相互独立的，先求解子问题，然后从这些子问题的解得到原问题的解。该算法的有效性依赖于问题本身所具有的两个重要性质：最优子结构性质和子问题重叠性质。

对于每个物品我们可以有两个选择，放入背包，或者不放入，有 n 个物品，故而我们需要做出 n 个选择，于是我们设 f[i][w] 表示做出第 i 次选择后，所选物品放入一个容量为 M 的背包获得的最大价值。

①如果能放入第 i 件物品，则 f[i][w] = f[i-1][W-w[i]]+v[i] ,表示，前 i-1 次选择后所选物品放入容量为 W-w[i] 的背包所获得最大价值为 f[i-1][W-w[i]] ，加上当前所选的第 i 个物品的价值 v[i] 即为 f[i][w] 。

②如果不放入第i件物品，则有 f[i][w] = f[i-1][w] ,表示当不选第 i 件物品时，f[i][w] 就转化为前 i-1 次选择后所选物品重量为w时的最大价值 f[i-1][w] 。

动态规划的选择方式：f[i][w] = max{ f[i-1][w] , f[i-1][W-w[i]]+v[i] }。
在这里插入图片描述

15.求解图着色问题

给定无向连通图G如下图所示，给定颜色种类为m。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。如果有一种着色法使G中每条边的两个顶点着不同颜色，则称这个图是可着色图。图的m着色问题是对于给定图G和m种颜色，假设m=3，找出所有不同的着色法。请用回溯法给出所有着色方案（请用1，2，3分别表示3种不同的颜色）
在这里插入图片描述
n=4，k=4，m=3，其着色方案有12个。

	顶点1　顶点2 　顶点3　顶点4
第1个着色方案	1　　　2　　　2　　　3
第2个着色方案	1　　　2　　　3　　　3
第3个着色方案	1　　　3　　　2　　　2
第4个着色方案	1　　　3　　　3　　　2
第5个着色方案	2　　　1　　　1　　　3
第6个着色方案	2　　　1　　　3　　　3
第7个着色方案	2　　　3　　　1　　　1
第8个着色方案	2　　　3　　　3　　　1
第9个着色方案	3　　　1　　　1　　　2
第10个着色方案	3　　　1　　　2　　　2
第11个着色方案	3　　　2　　　1　　　1
第12个着色方案	3　　　2　　　2　　　1

回溯法：
在这里插入图片描述

可一z可再

关注

2
点赞
踩
28

收藏

觉得还不错? 一键收藏
0
评论
计算机算法设计与分析——复习题

1.快速排序例题：对数组A={15，29，135，18，32，1，27，25，5}，用快速排序方法将其排成递增序列。简要回答快速排序的思想和上述数组的排序过程。基本思想　　在待排序的n个元素中任取一个元素（通常取第一个元素）作为基准，把该元素放入最终位置后，整个数据序列被基准分割成两个子序列，所有小于基准的元素放置在前子序列中，所有大于基准的元素放置在后子序列中，并把基准排在这两个子序列的中...
复制链接

扫一扫