【个人实验】直流有刷电机速度闭环控制+MATLAB参数辨识+PID Tuner整定参数

实验目的

• 通过MATLAB/SIMULINK对直流有刷电机进行系统辨识，得到模型，再使用PID Tuner和仿真系统得到合适的PID参数，实现速度、位置闭环控制，本次记录重点不在软硬件实现，主要为PID参数估算过程。

---

过程记录

1.通过串口得到满占空比时速度输出数据

2. 导入到MATLAB中绘制曲线并进行多项式拟合，在实时脚本中运行如图所示：

多项式拟合工具在figure工具中，可以在箭头按钮处将拟合的多项式系数导入到工作区，我选择的是十次多项式拟合。

使用多项式拟合的目的在于估算系统真正启动时的时间，从而获得整个系统的延迟时间，当然必要性不太大，因为主要目的是借此重新复习以下MATLAB多项式操作指令、数值求解算法、符号函数等，具体见脚本代码

clear,clc
time =[0.0230 0.0480 0.0730 0.0980 0.1230 0.1480 0.1730 0.1980 0.2230 0.2480 ...
    0.2730 0.2980 0.3230 0.3480 0.3730 0.3980 0.4230 0.4480 0.4730 0.4980 0.5230 ...
    0.5480 0.5730 0.5980 0.6230 0.6480 0.6730 0.6980 0.7230 0.7480 0.7730 0.7980 0.8230 0.8480] 
speed=[120.00 664.62  1116.92 1430.77 1624.62 1744.62 1827.69 1883.08 1929.23 1966.15 ...
     1984.62 2003.08 2012.31 2012.31 2012.31 2030.77 2049.23 2030.77 2021.54 2040.00 2076.92 ...
     2021.54 2030.77 2030.77 2040.00 2030.77 2021.54 2076.92 2030.77 2030.77 2030.77 2030.77 ...
     2030.77 2040.00]
 
% 多项式拟合
xishu=polyfit(time,speed,10);
% 创建时间数值向量
xi=0:0.025:34*0.025;
% 计算多项式的值
yi=polyval(xishu,xi);

plot(xi,yi,time,speed)
% 利用多项式系数创建符号
fx=poly2sym(xishu);

% gx=finverse(fx) % 求符号函数的反函数

% 求符号函数具体值的方法
g=matlabFunction(fx);
g(0.0184)

% bisect是自己实现的二分法数值求解函数
% 源码来自 https://zhuanlan.zhihu.com/p/158739301
delay = bisect(g,0.017,0.025,1e-9);   % delay = 0.018425
% 延迟环节系数可确定为0.018425

%计算去除系统延迟时间后电机自身的速度输出
speed_genuine = polyval(xishu,[0:0.005:160*0.005]);

% 生成PWM数据向量用于系统辨识
PWM=linspace(9999,9999,157);

3. 开始进行系统辨识
   import data 选择 time domin，好像可以多导入几组数据，我只用了一组
   
   估计了两个传递函数模型，一个连续一个离散准备两个都试试。
   
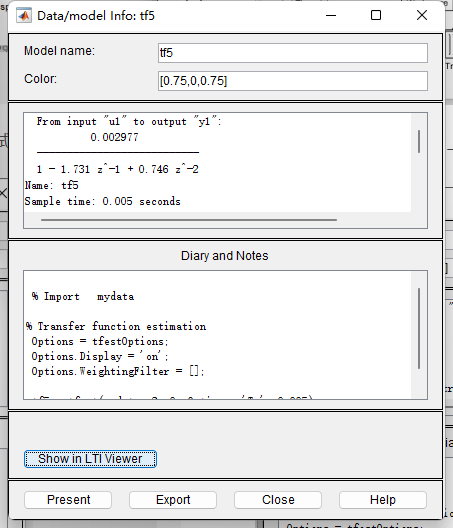
4. 搭建simulink仿真模型

• 加入延迟环节，饱和特性环节，死区特性环节
• 延迟环节 参数为0.018425
• 饱和特性 正负9999
• 死区特性 800
  使PID参数与MCU程序代码中的PID参数一致，测试仿真模型是否贴近实际控制系统
  中间使用from workspace模块，并在实时脚本中加入代码，创建导入到scope中的数据块

curspe= [0.00 120.00  498.46  913.85  1236.92 1541.54 1680.00 1753.85 1800.00 1827.69 1836.92 ...
    1855.38 1846.15 1846.15 1827.69 1809.23 1800.00 1781.54 1753.85 1735.38 1707.69 1670.77 ...
    1643.08 1615.38 1587.69 1560.00 1541.54 1504.62 1486.15 1476.92 1467.69 1458.46 1449.23 ...
    1458.46 1458.46 1476.92 1486.15 1495.38 1513.85 1523.08 1532.31 1550.77 1560.00 1569.23 ...
    1578.46 1578.46 1596.92 1587.69 1587.69 1606.15 1587.69 1587.69 1596.92 1587.69 1578.46 ...
    1587.69 1578.46 1569.23 1560.00]
tick=[23 47 71 95 119 144 169 194 219 244 269 294 319 344 369 394 419 444 469 494 519 544 ...
    569 594 619 644 669 694 719 744 769 794 819 844 869 894 919 944 969 994 1019 1044 1069 ...
    1094 1119 1144 1169 1194 1219 1244 1269 1294 1319 1344 1369 1394 1419 1444 1469]
plot(tick,curspe)

% 构建结构体数据块
si.time=tick'/1000; % 数据必须为列向量
si.signals.values=curspe'; % 数据必须为列向量
si.signals.dimensions=1;

测试结果：

说明搭建的模型准确度还凑合，可以用来继续进行PID参数整定。

4.使用PID Tuner进行PID整定

• 打开PID模块，从图中框选处打开PID Tuner，工具自动进行模型识别
  
• 拖动滑块，改变期望的输出特性，对应右下角给出对应的PID参数
  
  使用整定出来的PID参数用于实际控制系统中，效果与仿真结果有一定差距，但也比自己手动无头绪调参要好得多。