一维最大熵阈值分割法原理及实现

浮生有梦三千

已于 2022-02-12 19:55:59 修改

阅读量2k

点赞数 2

分类专栏： Opencv基础图像处理文章标签： python 算法开发语言

于 2022-02-12 14:39:58 首次发布

本文链接：https://blog.csdn.net/qq_44733143/article/details/122896380

版权

Opencv基础图像处理专栏收录该内容

5 篇文章 0 订阅

订阅专栏

# 一维最大熵阈值分割法原理及实现|CSDN创作打卡

背景

阈值分割：阈值分割是图像分割中的一种常用方法，通常是按阈值将图像分割成几个部分。

阈值分割方法的关键是阈值选取准则，常用的准则有最大类间方差（OTSU 大津法）和信息熵，其中大津法已经在上一篇博文中实现

OTSU算法（大津法—最大类间方差法）原理及实现

熵（ Entropy）

信息熵的概念是由信息论之父克劳德-香农所提出来的，和由物理学中的熵具有类似的公式，信息熵是用来衡量信息量大小的一个概念，具体可以参考这位博主的文章信息熵及其相关概念或者去哔哩哔哩上搜索信息熵来理解他的概念。

其中最重要的的一个性质就是：分布的越均匀，其熵越大，当系统内部所有的事件都是等概率发生时，其信息量越大，也就是熵越大。抽象到物理层面反过来理解就是：一个箱子隔成两个等体积部分，一边放1000个具有一定初速度的粒子，在里面自由运动，且能量不衰减，当把中间的隔板拿开，最后1000个粒子总会在箱子中趋向均匀分布，这就是系统熵增的一个过程，反过来理解就是熵越大越趋向于均匀分布。

那这与我们的图像分割有什么关系呢？阈值将图像所有的像素分为两类：前景和背景，当每一类像素中的像素在此类中趋向均匀分布时，此时这部分熵最大，当前景和背景两类像素都趋向均匀分布时，前景的熵和背景的熵最大，由系统熵的累加性，此时整幅图像的熵最大，即熵最大时将前景和背景区分开来。

hist

使用最大阈值法时，当灰度直方图为上图时，此时阈值为115，可以看出此时小于115阈值的像素在这类像素中趋向均匀分布，大于115阈值的像素在另一类中趋向均匀分布。

公式推导：

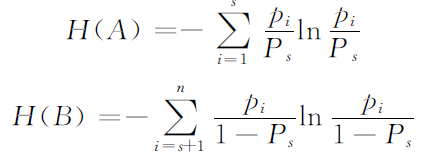
Opencv实现：

#include<opencv2/opencv.hpp>
#include<vector>
#include<iostream>


using namespace std;
using namespace cv;

void calcGrayHist(Mat& image, Mat& histImage)
{
	Mat hist;//用于存放直方图计算结果
	const int channels[1] = { 0 };//通道索引
	float inRanges[2] = { 0,255 };
	const float* ranges[1] = { inRanges };//像素灰度值范围
	const int bins[1] = { 256 };//直方图的维度，其实就是像素灰度值的最大值
	calcHist(&image, 1, channels, Mat(), hist, 1, bins, ranges);//计算图像直方图
	//准备绘制直方图
	int hist_w = 256;
	int hist_h = 400;
	int width = 1;
	histImage = Mat::zeros(hist_h, hist_w, CV_8UC3);
	for (int i = 1; i <= hist.rows; ++i) {
		rectangle(histImage, Point(width * (i - 1), hist_h - 1),
			Point(width * i - 1, hist_h - cvRound(hist.at<float>(i - 1))/2),//调整显示高度
			Scalar(255, 255, 255), -1);
	}

}



void Max_entropy(Mat input, Mat& output, int& thres,int deviation)
{
	const int Grayscale = 256;
	int width = input.cols;
	int height = input.rows;

	double Graystatistics[Grayscale] = { 0 };

	for (int i = 0; i < height; i++)
	{
		for (int j = 0; j < width;j++)
		{
			int Grayvalue = input.at<uchar>(i, j);
			Graystatistics[Grayvalue]++;//直方图统计

		}
	}

	double allnum = width * height;
	double Pi[Grayscale] = { 0 };//单个个灰度的概率
	double PS[Grayscale] = { 0 };//累计灰度概率
	

    double Psum = 0;
	for (int i = 0; i < Grayscale; i++)
	{
		Pi[i] = Graystatistics[i] / allnum;
		PS[i] = Pi[i] + Psum;
		Psum = PS[i];
	}

	
	double max_entropy = 0;

	for (int i = 0; i < Grayscale; i++)
	{
		double HA = 0;
		double HB = 0;
		//求前景熵
		double probility = 0;
		for (int j = 0; j < i; j++)
		{
			probility = 0;
			if (Pi[j] != 0)
			{
				probility = Pi[j] / PS[i];
				HA = HA +probility * log(1/probility);
				
			}
		}
		
		//求背景熵
		for (int m = i; m < Grayscale; m++)
		{
			probility = 0;
			if (Pi[m] != 0&&(1-PS[i])!=0)
			{
				probility = Pi[m] / (1 - PS[i]);
				HB = HB +probility * log(1/probility);

			}

		}
		if ((HA + HB) > max_entropy)
		{
			max_entropy = HA + HB;
			thres = i- deviation;
		}
		//cout << HA+HB << endl;
	}

	input.copyTo(output);
	for (int i = 0; i < height; i++)
	{
		for (int j = 0; j < width; j++)
		{
			int value = output.at<uchar>(i, j);
			if (value >thres)
			{
				output.at<uchar>(i, j) = 255;
			}
			else
			{
				output.at<uchar>(i, j) = 0;
			}
		}
	}
}



int main()
{
	Mat a = imread("mayi.png");
	cvtColor(a, a, COLOR_RGB2GRAY);
	Mat b;
	int th = 0;
	Max_entropy(a, b, th,0);
	cout << th << endl;
	Mat hist;
	calcGrayHist(a, hist);
	imwrite("2.bmp", b);
	imshow("1", b);
	return 0;
}