周报2023.7.7

卷积神经网络

• 理解卷积神经网络（CNN）的基本原理和结构。
• 学习CNN中常用的卷积层、池化层和全连接层的作用和操作。
• 掌握常用的CNN模型架构，如LeNet、AlexNet、VGG、ResNet等。
• 学习CNN模型的训练和优化技巧，包括学习率调整、正则化、批量归一化等。
• 实践使用深度学习框架（PyTorch）构建和训练CNN模型。

本周重点进行一二阶段

首先卷积神经网络的结构需要来一点官方的废话：

• 卷积层（Convolutional Layer）：卷积层是CNN中最重要的组成部分之一。它通过使用一组卷积核对输入数据进行卷积操作，从而提取特征信息。每个卷积核会滑动在输入数据上，并对其进行局部感知，产生输出特征图。

• 激活函数（Activation Function）：在卷积层中，激活函数通常被应用于卷积操作的结果，引入非线性性质。常用的激活函数包括ReLU（Rectified Linear Unit）、Sigmoid和Tanh等，它们能够引入非线性变换，增加模型的表达能力。

• 池化层（Pooling Layer）：池化层用于对卷积层输出的特征图进行下采样。常见的池化操作包括最大池化（Max Pooling）和平均池化（Average Pooling）。池化操作可以减小特征图的尺寸，并且具有平移不变性，提高模型的鲁棒性。

• 全连接层（Fully Connected Layer）：全连接层位于CNN的尾部，通常用于将高维特征映射到具体的类别或预测目标上。全连接层中的每个神经元都与前一层的所有神经元相连，通过学习权重来完成特征到预测结果的转换。

从BP到CNN

卷积的最后一个组件是BP，那么问题来了，为什么不直接BP？一来是说运算量的问题，全连接运算量太大了（然而现在算力应该也够了），说明卷积还是有他的道理。
BP的输入可以理解为复合型输入，比如鸢尾花的长度，宽度。然而我们输入的长度其实暗含了宽度等等信息的综合，是一种复合型的输入。但是在图像识别中输入是RGB属于是原子级别的信息基本，很单纯。所以需要经过卷积等操作将这些独立的信息结合成复合信息再输入到BP中进行最后的操作。

卷积

卷积公式：

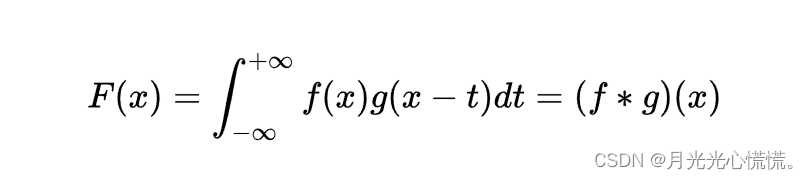
然而，CNN中对于卷积这一操作如下：

这两玩意儿有啥关系？难道只是单纯的撞名了?如果把特征看成$f$,卷积层看成$g$，最后得到的特征值就是$F$。这样一来好像确实可以对的上。那么问题来了，为什么要这么搞，有什么好处呢？想要弄清楚还得从源头慢慢来。

傅里叶变换

一提到卷积公式，相关搜索最多的就是傅里叶变换：$F(\omega )={\int }_{-\infty }^{\infty }f(t)e^{-i\omega t}dt$,这里用$e^{-i\omega t}$代替$g$。傅里叶变换是把时域中的表示转换为在频域中的表示：

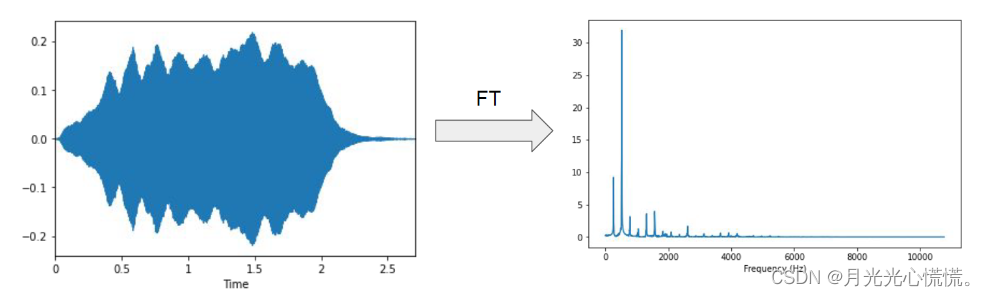
从公式本身可以发现一个好处：频域里面的一个点$\omega$的信息包含了整个时域的信息。左边$F(\omega )$就是一个点的值，而右边是整个时域的积分从负无穷到正无穷，是一个全局的信息。由此可以发现：CNN的目的与此相同，也是希望经过卷积后的每个信息点都包含了全局信息，也就是不再那么单纯了是复合型的信息，能被BP很好的发挥！
但是这样还有一点问题，就是全局信息是有了，但是不一定是好事。图像识别想要的是局部的信息，比如图片里有猫，有狗，我们希望提取信息的时候是把猫，狗局部分别提取特征，如果用全局信息就会变成猫与狗作为一个整体成为一个新的物种，这不是我们想要的结果，所以不能直接生搬硬套傅里叶变换。
那么下一步就是思考如何把把傅里叶变换的全局性加以限制，使其在局部生效。

希尔伯特空间

可以看做欧拉空间的一个plus版本，是无限维的空间，并且拥有以下性质：

• 内积运算：希尔伯特空间中定义了内积运算，它是一种将两个向量映射到复数的运算。内积运算满足线性性、对称性和正定性，并满足柯西-施瓦茨不等式和三角不等式。

• 完备性：希尔伯特空间是完备的，意味着其中的柯西序列在空间中有收敛的极限。这使得我们可以在希尔伯特空间中进行极限和收敛的操作。

• 正交性：希尔伯特空间中的向量可以相互正交。两个向量正交表示它们的内积为零，这对于定义垂直关系和正交基是非常有用的。

无限维空间中的一个点可以看成$\mathbf{x}=(x_1,x_2,\cdots ,x_{\infty })$,如果我们把这无数个值放到二维坐标轴中就会得到一条曲线。等价于是二维坐标的一条曲线，在无穷维中可以被一个点表示。空间中的点又可以用向量来等价表示，现在我们在希尔伯特空间中找一个新的基${\mathbf{d}}_{\infty }$，有如下式子：$|{\mathbf{x}}^0|\cdot {\mathbf{d}}_{\infty }=|\mathbf{x}|\cdot \left|{\mathbf{d}}_{\infty }\right|\cdot \cos \theta \cdot \frac{{\mathbf{d}}_{\infty }}{|{\mathbf{d}}_{\infty }|}=⟨\mathbf{x},{\mathbf{d}}_{\infty }⟩\cdot {\hat{d}}_{\infty }$,这里${\mathbf{x}}^0$是在新基下的投影，$⟨\mathbf{x},{\mathbf{d}}_{\infty }⟩$是原始向量与新基的内积，${\hat{d}}_{\infty }$表示新基的单位向量。把内积写成积分形式有：${\hat{d}}_{\infty }\cdot {\int }_{-\infty }^{+\infty }f(x)d_{\infty }(x)dx$，这样一来傅里叶变换就可以看成希伯尔特空间中的一个基变换，只是这里选用的是$e^{-i\omega t}$作为基，而且最重要的是将这个基用原始空间来表示会发现这个函数覆盖了全局，这既是为什么傅里叶变换有全局性的原理。
如果不想要全局信息只需要对基的选取加以限制即可，使得限制后选取的基在原始的基中不在覆盖全局。比如拉普拉斯变换就是加以基指数限制后的傅里叶变换。
回到卷积神经网络的卷积层，我们一般选择3*3的大小，就相当于做了一个限制，所以卷积操作的每一步都是有据可依的。

池化

目前没有发现有什么科学原理，可能是单纯的因为做图像识别用不到高清的信息，只需大概的就行。如果把池化前的信息看做是高清图，那么池化后的就是马赛克图，但是不影响能够识别马赛克是什么。