正规式生成NFA和DFA

1. 问题描述
   给定正规式，自动生成NFA和DFA，并以表得形式输出NFA和DFA。
2. 算法设计
   整行读入正规式后，逐字遍历，生成item数组，item数组第一个元素是空转移，用e表示。然后重新遍历正规式，每遇到一个不是*的字符均生成一个新状态，并根据扫描到得字符进行不同得操作。与此同时生成NFA表。具体流程图如图1所示。
   
   得到NFA后，在nfa即table表的基础上得到DFA。定义一个二维向量组dfatable来存储DFA。在声明一个二维向量存储各DFA状态包含的NFA状态集。声明一个队列记录生成的还未得到下一个转换状态的DFA状态。具体处理流程图如图2所示。

3. 实验代码

#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<iomanip>
#include<algorithm>
#include<queue>

using namespace std;

int familiar(vector<vector<int>>& table, vector<int>& t,int num) {
	
	sort(t.begin(), t.end());
	int flag;
	for (int i = 0; i < num; i++) {
		sort(table[i].begin(), table[i].end());
		flag = 0;

		if (t.size() == table[i].size()) {
			
			for (int j = 0; j < t.size() && flag==0; j++) {
				if (t[j] != table[i][j])
					flag = 1;
			}
			if (flag == 0)
				return i;

		}
	}
	return -1;
}


//输出dfa
void show(vector<vector<int>>& dfa, int num,int iter)
{
	
	for (int i = 0; i < num; i++)
	{
		
		cout << setiosflags(ios::left) << setw(10) << i;//输出状态
		for (int j = 0; j < iter; j++)
		{
			if(dfa[i][j]==NULL)
				cout << setw(10) << setfill(' ') << "-1";
			else {
				cout << setiosflags(ios::left) << setw(10);
				cout << dfa[i][j] ;
			}
		}
		cout << endl;
	}
}
//输出函数，答应dfa或nfa的表
void display(vector<vector<stack<int>>>& table,int x,int y) {
	for (int i = 0; i < x; i++) {
		cout << setiosflags(ios::left) << setw(10)<< i ;
		for (int j = 0; j < y; j++) {
			cout << setw(10) << setfill(' ');
			
			vector<int> temp;
			int m = 0;
			if(table[i][j].empty())
				cout << setw(10) << setfill(' ')<<"-1";
			else {
				while (!table[i][j].empty()) {
					cout << setiosflags(ios::left) << setw(0);
					cout << table[i][j].top()<<',';
					temp.push_back(table[i][j].top());
					m++;
					table[i][j].pop();
				}
				cout << setw(9) << setfill(' ')<<' ';
				for (; m > 0; m--) {
					table[i][j].push(temp[m - 1]);
				}
			}
		}
		cout << endl;
	}
}/**/

//在数组中找到字符的位置，若没找到返回-1
int search(vector<char>& item, char s) 
{
	for (int i = 0; i < item.size(); i++) {
		if (item[i] == s) return i;
	}
	return -1;
}
/**/
int main() {
	string str;
	getline(cin,str);
	
	  
	int iter = 0;//记录item表的size，对应位置为空
	int length = 0;
	vector<char> item;//记录表的横向变量
	item.push_back('e');
	iter++;
	for (int i = 0; i < str.length(); i++) {//遍历正规式，生成item表
		if (str[i] == '(' || str[i] == ')' || str[i] == '+')
			length++;
		else if (str[i] == '*')
			continue;
		else if (search(item, str[i])== -1) {
			item.push_back(str[i]);
			iter++;
			length++;
		}
		else {
			length++;
		}
	}
	length++;
	//遍历生成table
	
	vector<vector<stack<int>>> table(length);
	for (int i = 0; i < length; i++) {
		table[i].resize(iter);
	}
	
	stack<int> kuohao;//记录遇左括号之前的状态
	int x = 0;//记录状态数
	stack<int> path;//有多条路径时，记录路径的最后状态 

	for (int i = 0; i < str.length(); i++) {
		x++;
		switch (str[i])
		{
		case '(': {
			kuohao.push(x - 1);
			table[x-1][0].push(x);
			break;
		}
		case '+': {
			path.push(x - 1);
			table[kuohao.top()][0].push(x);
			break;
		}
		case ')': {
			if (str[i + 1] == '*') {
				i++;
				table[x][0].push( kuohao.top());
				table[kuohao.top()][0].push(x);
			}
			table[x - 1][0].push(x);
			while (!path.empty()) {
				table[path.top()][0].push(x);
				path.pop();
			}
			kuohao.pop();
			break;
		}
		case '*': {
			x--;
			int w = search(item, str[i - 1]);
			table[x][w].push(x);
			break;
		}
		default: {
			int w = search(item, str[i]);
			table[x - 1][w].push(x);
			break;

		}
			
		}
	}
	
	
	cout << "NFA: \n";
	cout << setw(10) << setfill(' ')<<' ';
	for (int i = 0; i < iter; i++) {
		cout << setiosflags(ios::left) << setw(10);
		//cout << setw(10) << setfill(' ') << item[i];
		cout<< item[i];
	}
	cout << endl;
	display(table, length, iter);/**/
	//--------------------------------------------------------------------------------------
	//转DFA
	//--------------------------------------------------------------------------------------
	int num=0;//存储DFA状态数
	vector<int> temp;
	vector<vector<int>> status(length+1);//存储各状态包含的nfa状态集

	vector<vector<int>> dfatable(length);//构建dfa表
	
	for (int i = 0; i < length; i++) {
		dfatable[i].resize(iter - 1);
	}

	num++;
	status[0].push_back(0);//状态0
	while (!table[0][0].empty()) 
	{
		status[0].push_back(table[0][0].top());
		temp.push_back(table[0][0].top());
		table[0][0].pop();
	}
	for (int i = 0; i < temp.size(); i++) {
		table[0][0].push(temp[i]);
	}
	temp.clear();

	queue<int> tmp;
	tmp.push(0);
 
	while(!tmp.empty())
	{
		int x;
		x = tmp.front();
		
		tmp.pop();
	
		for (int i = 1; i < iter; i++)//对不同的输入产生不同的状态 
		{
			num++;//状态x对输入iter产生新的状态
			for (int j = 0; j < status[x].size(); j++) {//产生新状态得nfa状态集合
				
				while (!table[status[x][j]][i].empty()) {
					
					status[num-1].push_back(table[status[x][j]][i].top());
					temp.push_back(table[status[x][j]][i].top());
					table[status[x][j]][i].pop();
				}
				for (int a = 0; a < temp.size(); a++) {
					table[status[x][j]][i].push(temp[a]);
				}
				temp.clear();
			}
			
			sort(status[num - 1].begin(), status[num - 1].end());
			status[num - 1].erase(unique(status[num - 1].begin(), status[num - 1].end()), status[num - 1].end());
			for (int j = 0; j < status[num - 1].size(); j++) {//更新下一状态的nfa状态集
				while (!table[status[num - 1][j]][0].empty()) {
					//若列表中没有空转移的末状态，则将该状态加入列表
					vector<int>::iterator result = find(status[num - 1].begin(), status[num - 1].end(), table[status[num - 1][j]][0].top());
					if (result == status[num - 1].end()) {
						status[num - 1].push_back(table[status[num - 1][j]][0].top());
						
					}

					temp.push_back(table[status[num - 1][j]][0].top());
					table[status[num - 1][j]][0].pop();
				}
				
				for (int i = 0; i < temp.size(); i++) {
					table[status[num - 1][j]][0].push(temp[i]);
				}
				temp.clear();
			}
			
			int flag = familiar(status, status[num - 1], num - 1);
			
			if (status[num - 1].empty()) {
				num--;
			}
			else if (flag!=-1 ) //若两状态集合相同，则不产生新状态
			{
				dfatable[x][i - 1] = flag;
				status[num - 1].clear();
				num--;
			}
			else {
				dfatable[x][i-1] = num - 1;
				tmp.push(num - 1);
			}
		}
		
	}

	dfatable.resize(num);

	//输出dfa
	cout << "DFA: \n";
	cout << setw(10) << setfill(' ') << ' ';
	for (int i = 1; i < iter; i++) {
		cout << setiosflags(ios::left) << setw(10);
		//cout << setw(10) << setfill(' ') << item[i];
		cout << item[i];
	}
	cout << endl;
	show(dfatable, num,iter-1);
	return 0;
}

4. 测试结果
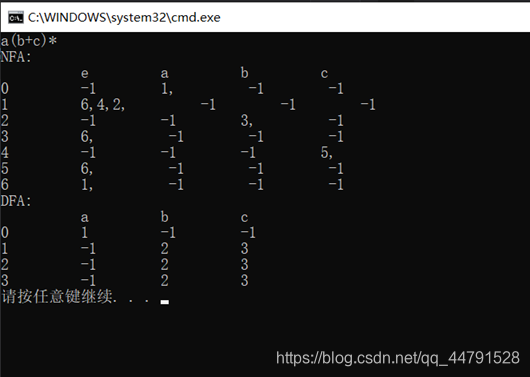
   分别以课后作业的例子进行测试，输入正规式a(a+b)、a(b+c)、ab*等进行测验，得到结果如图3、4、5所示。其中-1表示没有该转移。