人工神经网络ANN学习笔记（一）

定义：人工神经网络（Artificial Neural Network），它是人脑神经元网络的抽象，是一种运算模型，由大量的节点（或称神经元）相互联接构成。每个节点代表一种特定的输出函数，称为激活函数。每两个节点间的连接都代表一个对于通过该连接信号的加权值，称之为权重。网络的输出则依网络的连接方式，权重值和激励函数的不同而不同。而网络自身通常都是对自然界某种算法或者函数的逼近，也可能是对一种逻辑策略的表达。

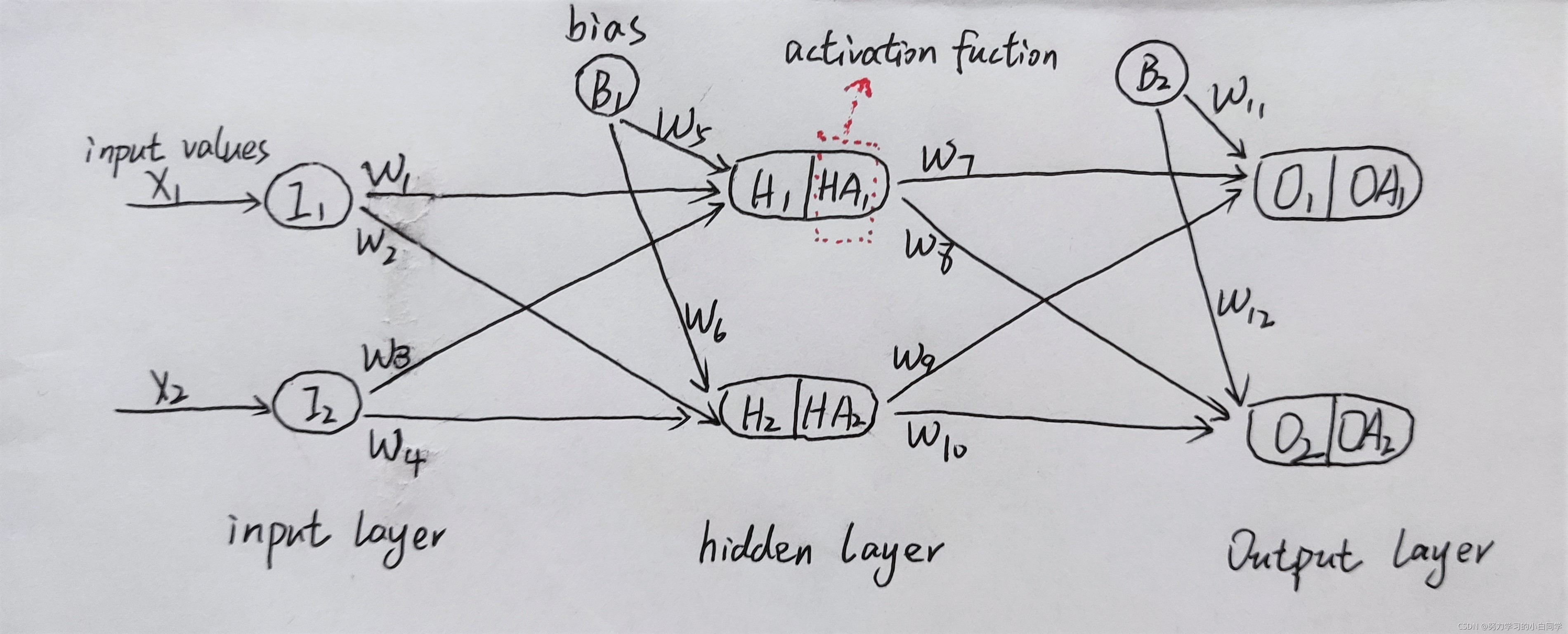
 注：1.样本有多少个feature，输入层就有多少个节点。

2.根据组合的情况来设定权重，权重要进行初始化。

下面以手写体数字识别为例继续学习ANN

数据集简介：MNIST数据集，60000个样本用于学习，10000个样本用于测试，每一个样本都是28*28点阵图，共784个像素点，每个像素点的值从0-255。 每个样本的784个像素点的值就是feature，每个样本的数字就是label。

从输入到输出的过程叫做前向传播（forward propagation），输入层有784个节点，隐藏层根据需要自己设置，每个节点的输入值乘以对应的权重的和送入激活函数，依此类推。输出可以设置一个节点，输出0-9这十个类别；也可以设置十个节点，输出一种概率分布，比如0.8的概率为“0”，0.1的概率是“6”，0.05的概率是“8”……

 

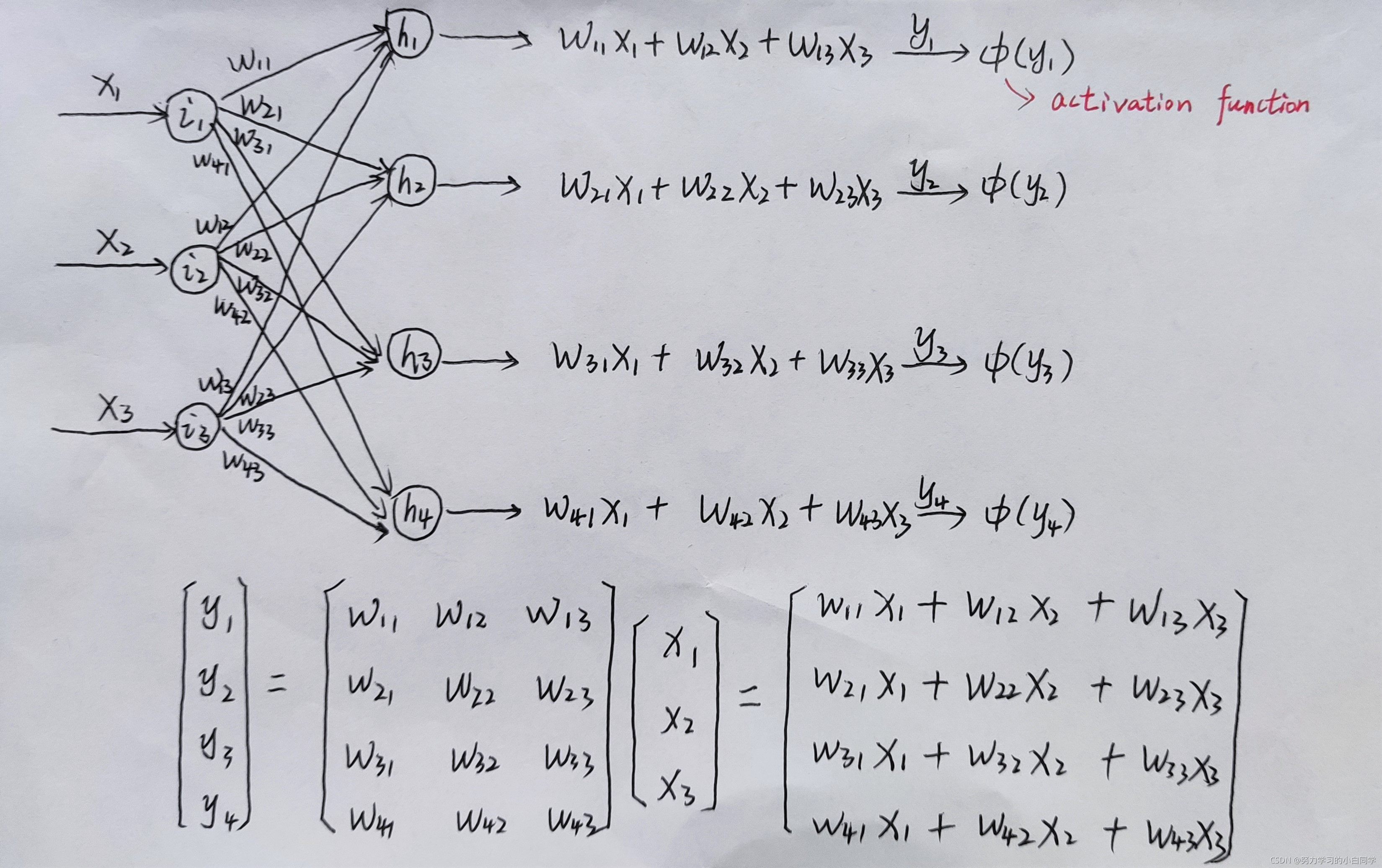
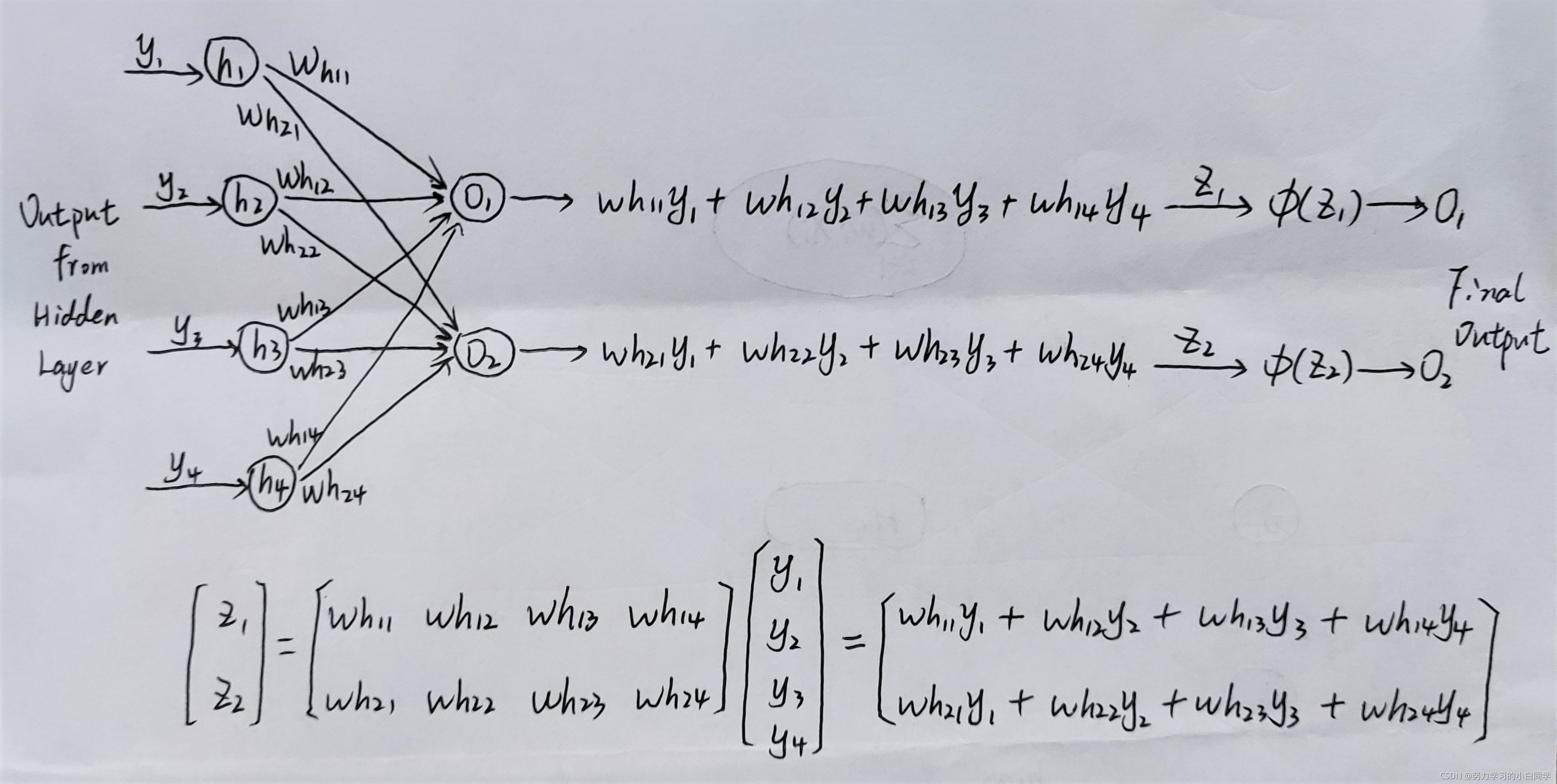
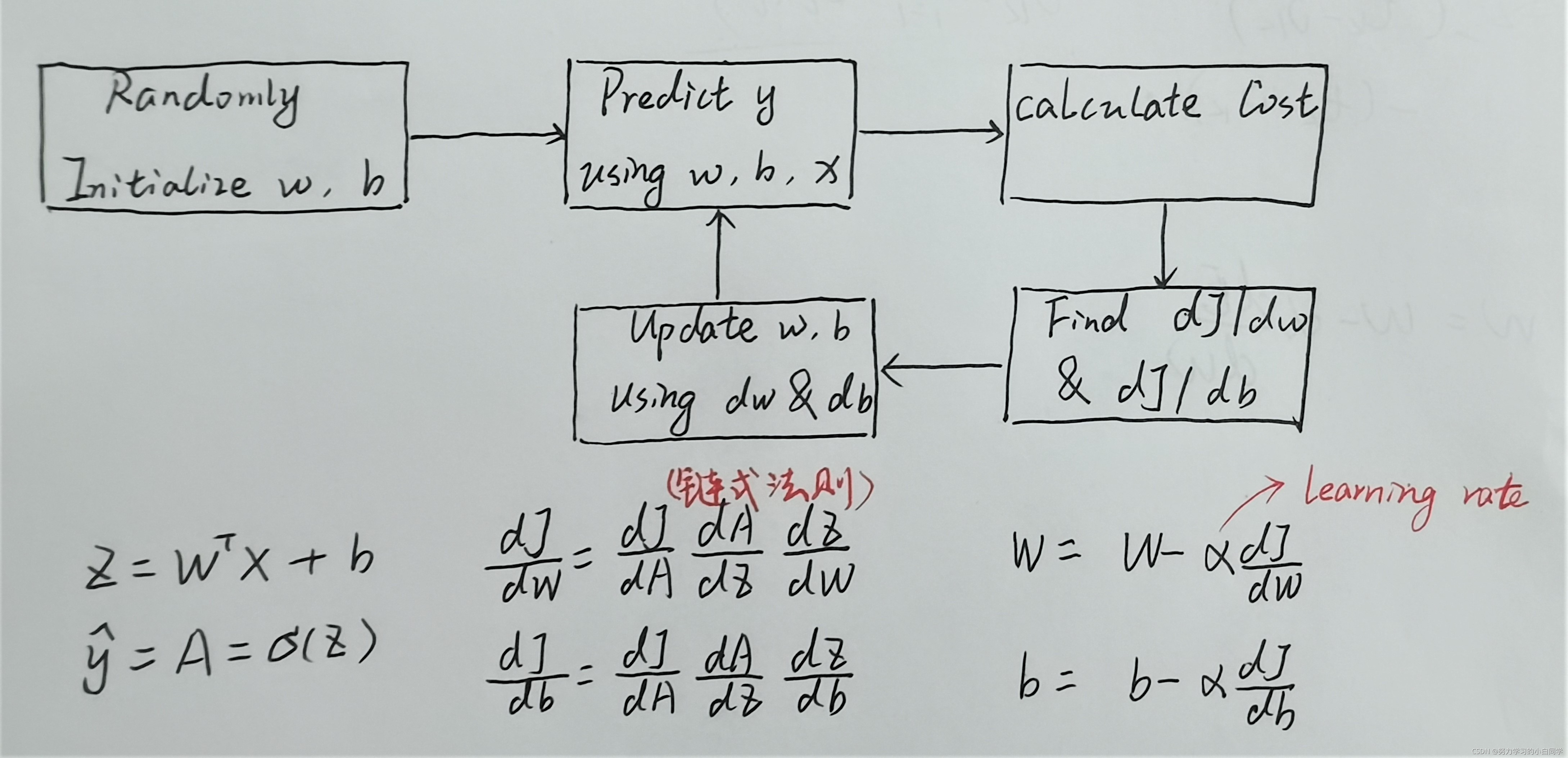
 当输出值和目标值之间有差距时，就定义了一个损失函数（cost function），将损失返回回去，来寻找一个新的权重的组合，再算一遍输出，使其更接近目标值，这个过程就叫做反向传播(back propagation)。

如何初始化权重向量

1.生成半开区间上的均匀分布

##生成1000个从-1到0区间上的均匀分布
import numpy as np

mumber_of_samples = 1000
low = -1
high = 0
s = np.random(low, high, number_of_samples)

2.生成二项式分布

##100次试验，每次成功的概率为0.5
import numpy as np

s = np.random.binomial(100, 0.5, 1000)

3.numpy.random.normal不能指定区间值，引入scipy.stats.truncnorm

import numpy as np

def truncated_normal(mean=0, as=1, low=0, upp=10):
    return truncnorm(
                     (low - mean) / sd, (upp - mean) / ad, loc=mean, scale=sd)

no_of_input_nodes = 3
no_of_hidden_nodes = 4
rad = 1 / np.sqrt (no_of_input_nodes)

X = truncated_normal (mean=2, sd=1, low=-rad, upp=rad)
wih = X.rvs((no_of_hidden_nodes, no_of_input_nodes))

激活函数(activation function)

只能对输入值进行线性处理，引入激活函数就可以进行非线性处理了，这样神经网络就可以应用到众多的非线性模型中。下面是几种激活函数：

1.sigmoid 

可以将变量非线性映射到0,1之间，定义为：

它的导数可以用其自身来表示：

2.ReLU (Rectified Linear Unit)

3.Softmax

映射区间[0,1]，主要用于离散化概率分布

损失函数（以Squared Error Loss为例）

为了优化输出，我们要使用损失函数。设每个节点目标输出为，ANN的实际输出为，则误差,下面是推导过程：

 如何评价预测模型

混淆矩阵（Confusion Matrix，cm）

准确率（Accuracy）       精确率（Precision）      召回率（Recall）

	predicted
actual		negative	positive
	negative	TN	FP
	positive	FN	TP

精确率是对于预测结果而言的，简言之，预测为正的结果里有多少是对的。

召回率是对于原来的样本而言的，简言之，原来为正的样本有多少被预测对了。

准确率是对于全部样本而言的，表示所有的样本有多少被准确地预测了。