支持向量机

一、间隔（margin）

1.支持向量机基本原理
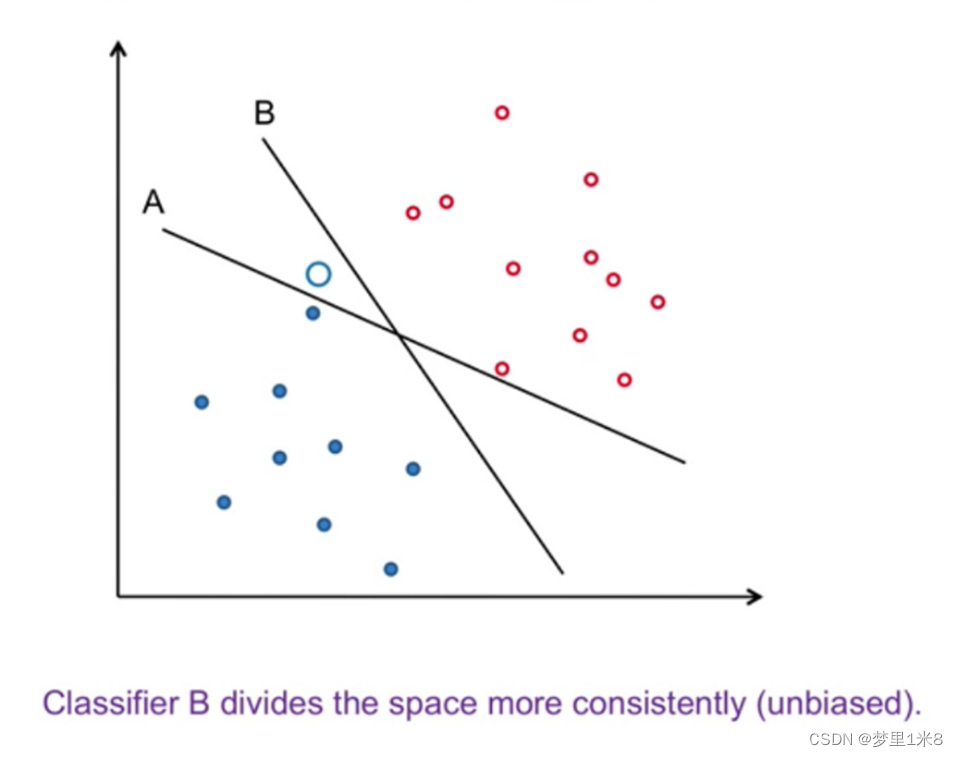
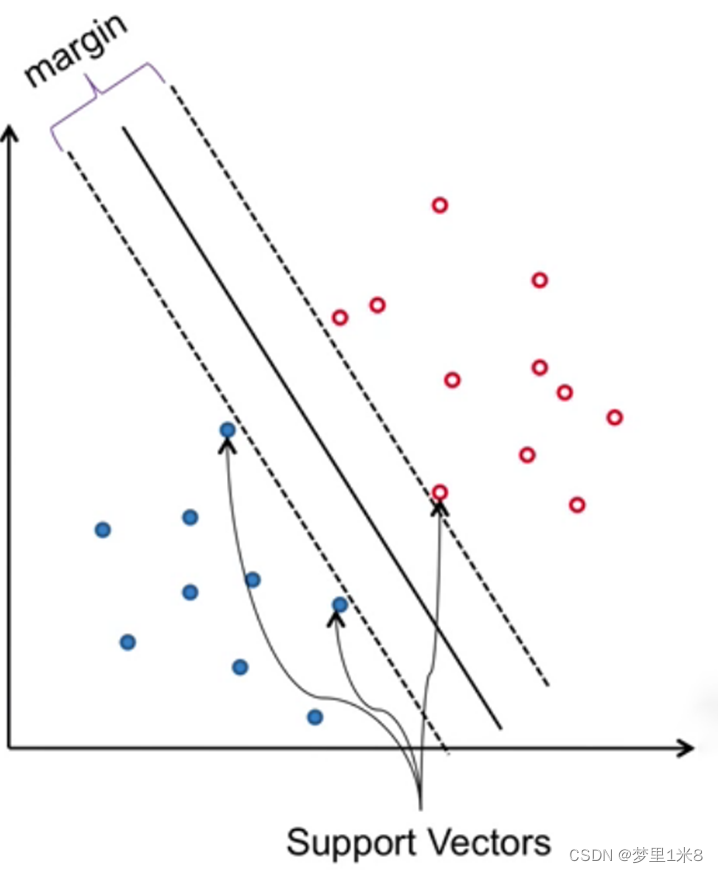
对一个二分类问题，在线性可分的情况下，可以找到泛化能力最强的最大间隔超平面（Maximum Marginal Hyperplane，MMH）如图 1. 1将两类样本分开的超平面中B，使得间隔（margin）最大如图 1. 2间隔，距离MMH最近的样本点称为支持向量（Support Vector）。与其他模型相比，SVM算法不太容易发生过拟合问题。

在非线性可分的情况下，用非线性映射把输入数据变换到较高维的空间，在新的空间中找到最大间隔超平面对应于原空间中的非线性分离超曲面。

2.如何最大化margin
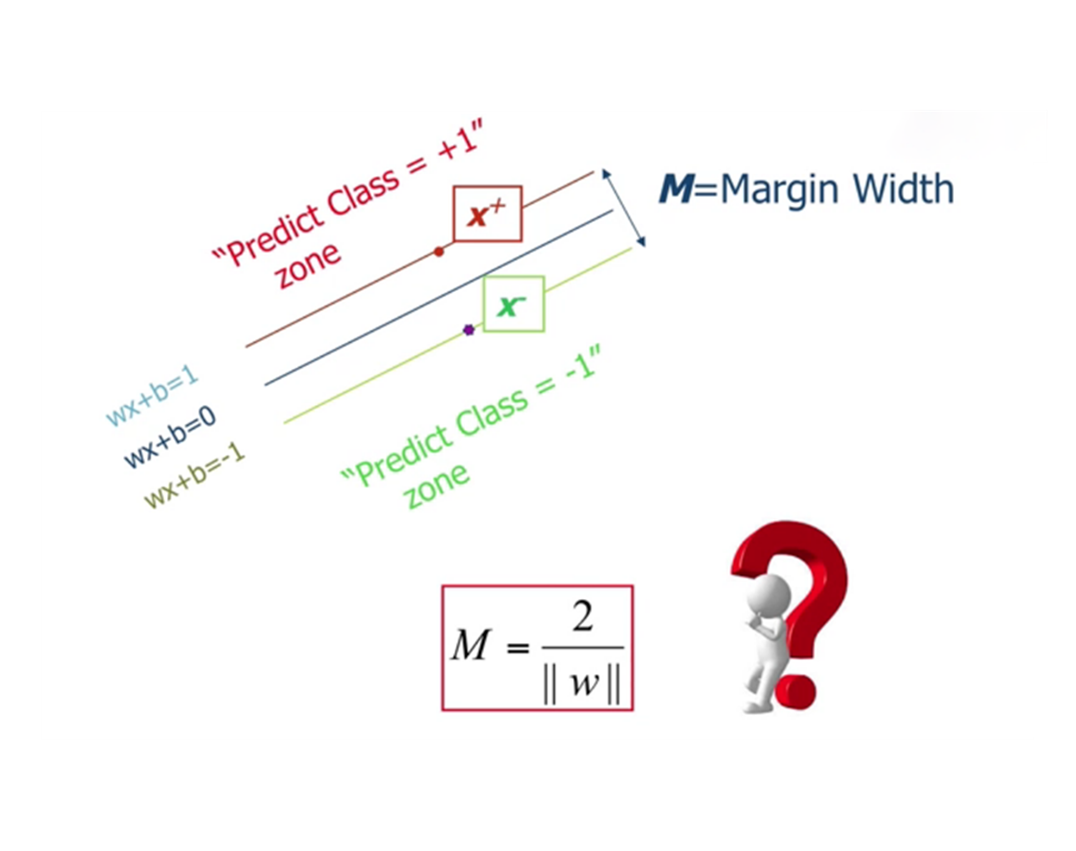
如图 1. 4超平面表达式所示，决策边界（最大间隔超平面）用w·x+b=0表示，其中w为超平面的法向量，决定超平面的方向，b为位移项通常称为偏倚（bias），决定超平面与原点之间的距离。支持向量所在的超平面分别定义为w·x+b=1和w·x+b=-1，其间隔为γ = 2/(||w||)。
要找到最大间隔超平面，就得找到满足{(w·x+b≥1@w·x+b≤1)}的参数w和b，使得γ最大，即
(_w,b^max) 2/(||w||)
s.t. y_i (wx_i+b)≥1, i=1,2,⋯,m
最大化2/(||w||)，相当于最小化||w||^2（为方便求导，转换为1/2||w|| ^2 ），于是可写为
(_w,b^min) 〖1/2||w||〗^2
s.t. y_i (wx_i+b)≥1, i=1,2,⋯,m

二、对偶

1. 拉格朗日乘子
   用拉格朗日乘数法解决有约束条件（等式约束）的极值问题，引入拉格朗日乘子(Lagrange multiplier)，构建拉格朗日函数，具体实现步骤如下：
2. KKT条件
   针对既有等式约束又有不等式约束的模型，例如对下列问题的求解。
   构造拉格朗日函数：
   对拉格朗日函数求导，得出极值点，满足KKT条件：
3. 对偶
   在等式约束条件h_i (x)=0和不等式约束条件g_i (x)≤0下，求f(x)的最小值。
   构造拉格朗日函数：
   在满足KKT条件的情况下，将拉格朗日函数先最大化在最小化，与原问题等价。
   对偶优化：
   当且仅当满足KKT条件时取等号，原优化问题可通过对偶问题求解。
4. 对偶在SVM上的应用
   原问题为：
   构造拉格朗日函数：
   L(w,b,α)=〖1/2||w||〗^2-∑_(i=1)n▒〖α_i [y_i (w^T x_i+b)-1]〗
   令L(w,b,α)对w,b求偏导为0，将结果带入拉格朗日函数，得：
   对偶问题：
   解出α_i，求得w,b即可得到模型
   f(x)=w^T x_i+b=∑_(i=1)^m▒〖α_i y_i x_i^T x+b〗
   其满足KKT条件，故对任意训练样本(x_i,y_i)，总有α_i=0或y_i f(x_i)=1。
   对于对偶问题的求解，可使用通用的二次规划算法来求解，然而该问题的规模正比于样本数，会造成很大的开销。对于解决这个问题，有很多高效的算法，例如SMO。
5. SMO算法
   SMO就是要解这个凸二次规划问题，这里的C是个很重要的参数，它从本质上说是用来折中经验风险和置信风险的，C越大，置信风险越大，经验风险越小；并且所有的拉格朗日乘子都被限制在了以C为边长的大盒子里。SMO的出现使得我们不必去求助于昂贵的第三方工具去解决这个凸二次规划问题。其思想类似坐标上升算法，我们需要优化一系列的α的值，我们每次选择尽量少的α来优化，不断迭代直到函数收敛到最优值。
   简化版SMO算法：检查训练样本中每个点 是否满足KKT条件，如果不满足，则它对应的α_i可以被优化，然后随机选择另一个变量α_j进行优化。简化版的SMO算法在小数据集上没什么问题，但遇到大数据集速度就会变得很慢。完整版的算法与简化版的算法唯一不同的就是α的选择。
   ##三、核函数
6. 基本思想
   对于非线性可分问题，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分（如果原始空间是有限维的，即属性有限，那么一定存在一个高维特征空间使样本可分）。
7. 具体方法
   令ф(x)表示将x映射后的特征向量，在特征空间中划分超平面所对应的模型表示为：
   f(x)=w^T ϕ(x)+b
   w,b是模型参数，其对偶问题为
   (α^{max)∑_(i,j=1)}m▒〖α_i α_j y_i y_j 〖ϕ(x_i )〗^T ϕ(x_j ) 〗
   s.t.∑(i=1)^m▒〖α_i y_i=0〗,
   α_i≥0, i=1,2,⋯,m
8. 核函数
   求解上述对偶问题需要计算〖ϕ(x_i )〗^T ϕ(x_j )，这是样本x_i与x_j映射到特征空间之后的内积。由于特征空间维度很高，甚至无穷维，因此计算起来十分困难。为了解决这个困难，设想一个函数，如下：
   k(x_i,x_j )=<ϕ(x_i ),ϕ(x_j )>=〖ϕ(x_i )〗^T ϕ(x_j )
   重写后求解可得到：
   上式显示出模型最优解可通过训练样本的核函数展开，这一展式已成为“支持向量展式”（support vector expansion）。
   常见的核函数有：h次多项式核函数、高斯径向基函数核函数、S型核函数等。
9. 核函数定理
   令χ为输入空间，k( * , * )是定义在χxχ上的对称函数，则k是核函数当且仅当对于任意数据D={x1,x2,⋯,xm}，“核矩阵”（kernel matrix）K总是半正定的。
10. 核方法
    人们发展出一系列基于核函数的学习方法，统称为“核方法”（kernel methods）。最常见的是通过“核化”（即引入核函数）来将线性学习器拓展为非线性学习器。
    四、软间隔与正则化
    软间隔容许某些样本不满足约束：y_i (wx_i+b)≥1，在最大化间隔的同时，不满足约束的样本应尽可能少。在引入软间隔理论后，我们的优化目标就变成了下面的形式：
    这里 C>0为 惩罚参数，可以理解为我们一般回归和分类问题正则化时候的参数， C越大，对于误分类的惩罚越大，反之越小。也就是说我们希望目标函数尽量小，误分类的点尽可能的少。CC是协调两者关系的正则化惩罚系数。
    经过拉格朗日乘数法和对偶问题的应用，最终化为：
    五、总结
    支持向量机的优势：泛化性能比较好, 不容易过拟合，可以在较少的数据下取得好的性能，存在全局最优解，存在高效实现的训练算法，可以使用kernel trick处理非线性的问题，大规模训练样本（m阶矩阵计算） 速度慢。缺点：传统的SVM不适合多分类，对缺失数据、参数、核函数敏感。大规模训练样本（m阶矩阵计算） 速度慢。