深度学习 神经网络中的前向传播和反向传播算法推导

                                   

               

1. 神经网络

这是一个常见的神经网络的图：

这是一个常见的三层神经网络的基本构成，Layer L1是输入层，Layer L2是隐含层，Layer L3是隐含层，当我们输入x1,x2,x3等数据时，通过隐含层的计算、转换，输出你的期望，当你的输入和输出是一样的时候，成为自编码模型（Auto-Encoder）,而当你输入和输出是不一致的时候，也就是我们常说的人工神经网络。

2.  如何计算传播

首先我们先构建一个简单的网络层作为例子：

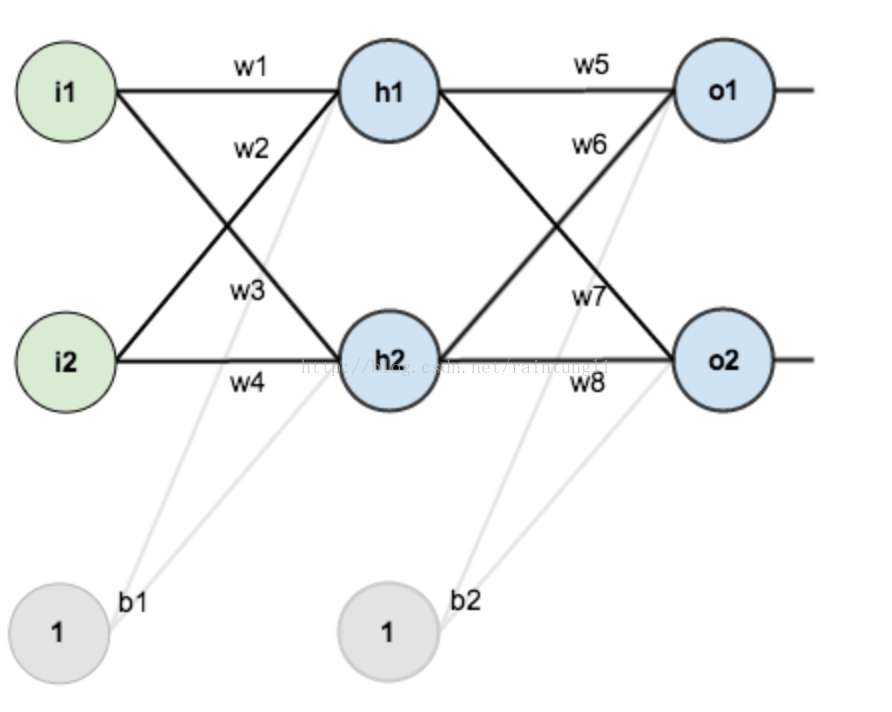
在这个网络层中有

• 第一层输入层：里面包含神经元i1,i2，截距：b1，权重：w1,w2,w3,w4
• 第二层是隐含层：里面包含h1,h2，截距：b2，权重：w5,w6,w7,w8
• 第三层是输出层：里面包含o1,o2

我们使用sigmoid作为激活函数

PS:如果你觉得这篇文章看起来稍微还有些吃力，或者想要系统地学习人工智能，那么推荐你去看床长人工智能教程。非常棒的大神之作，教程不仅通俗易懂，而且很风趣幽默。点击这里可以查看教程。

假定我们输入数据 i1: 0.02 i2: 0.04 截距 b1:0.4 b2:0.7 期望的输出数据 o1:0.5  o2:0.9

未知的是权重w1,w2,w3,w4,w5,w6,w7,w8

我们的目的 是为了能的到o1:0.5 o2:0.9的期望的值，计算出w1,w2,w3....w8的权重值

先假如构造一个权重w1,w2,w3.....w8的值，通过计算获取到最佳的w1,w2,w3....w8的权重

权重的初使值：

   
   

     
     

      
      

     
     
     
     

      
      

       
       w1=0.25
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w2=0.25
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w3=0.15
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w4=0.20
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w5=0.30
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w6=0.35
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w7=0.40
      
      
     
     

     
     

      
      

     
     
     
     

      
      

       
       w8=0.35
      
      
     
     
   
   

   
   
1

2.1 前向传播

2.1.1 输入层到隐含层

NET(h1)=w1*i1+w2*i2+b1=0.25*0.02+0.25*0.04+0.4=0.005+0.01+0.4=0.415

神经元h1到输出h1的激活函数是sigmoid

OUT(h1)=1/(1+e^(-NET(h1)))=1/(1+0.660340281)=0.602286177

同理我们也可以获取OUT(h2)的值

NET(h2)=w3*i1+w4*i2+b1=0.15*0.02+0.20*0.04+0.4=0.003+0.008+0.4=0.411

OUT(h2)=1/(1+e^(-NET(h2)))=1/(1+0.662986932)=0.601327636

2.1.2 从隐含层到输出层

计算输出层的神经元o1, o2的值，计算方法和输出层到隐含层类似

NET(o1)=w5*h1+w6*h2+b2=0.3*0.602286177+0.35*0.601327636+0.7=0.180685853+0.210464672+0.7=1.091150525

OUT(o1)=1/(1+e^(-NET(o1)))=1/(1+0.335829891)=0.748598311

同理

NET(o2)=w7*h1+w8*h2+b2=0.4*0.602286177+0.35*0.601327636+0.7=0.240914471+0.210464672+0.7=1.151379143

OUT(o2)=1/(1+e^(-NET(o2)))=1/1.316200383=0.759762733

o1:0.748598311   o2:0.759762733 距离我们期望的 o1:0.5  o2:0.9还是有很大的距离

2.2 计算总误差

公式：

也就是我们需要计算每个期望误差的和

E(total)= E(o0)+E(o1)=(1/2)*(0.748598311-0.5)^2+(1/2)*(0.759762733-0.9)^2=0.01545028+0.009833246=0.025283526

2.3 反向传播

每一个权重对误差的影响，我们可以通过下图更直观的看清楚误差的反向传播

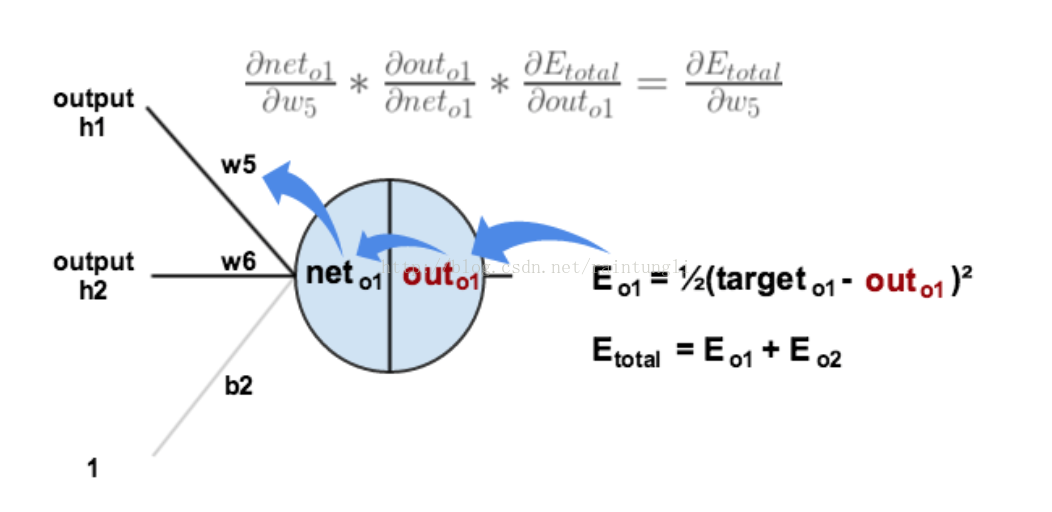
2.3.1 隐含层到输出层的权值更新

隐含层到输出层的权值，在上面的例子里是W5,W6,W7,W8

我们以W6参数为例子，计算W6对整体误差的影响有多大，可以使用整体误差对W6参数求偏导：

很明显并没有W6对Etotal的计算公式，我们只有W6对Net(o1)的计算公式

但根据偏导数的链式法则，我们可以将我们存在的推导公式进行链式乘法

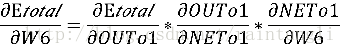
我们来计算每一个公式的偏导：

• 计算：

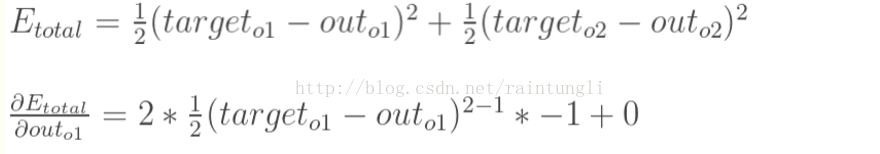
这是一个复合函数的导数

设{\displaystyle f}和{\displaystyle g}为两个关于{\displaystyle x}可导函数，则复合函数{\displaystyle (f\circ g)(x)}的导数{\displaystyle (f\circ g)'(x)}为：

{\displaystyle (f\circ g)'(x)=f'(g(x))g'(x).}

这里g(x)=target(o1)-out(o1)  g'(x)=-1

=-(0.5-0.748598311)=0.248598311

• 计算

已知

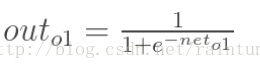
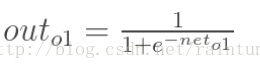
我们来推导一下 ：

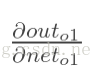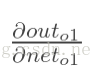还是复合函数的推导

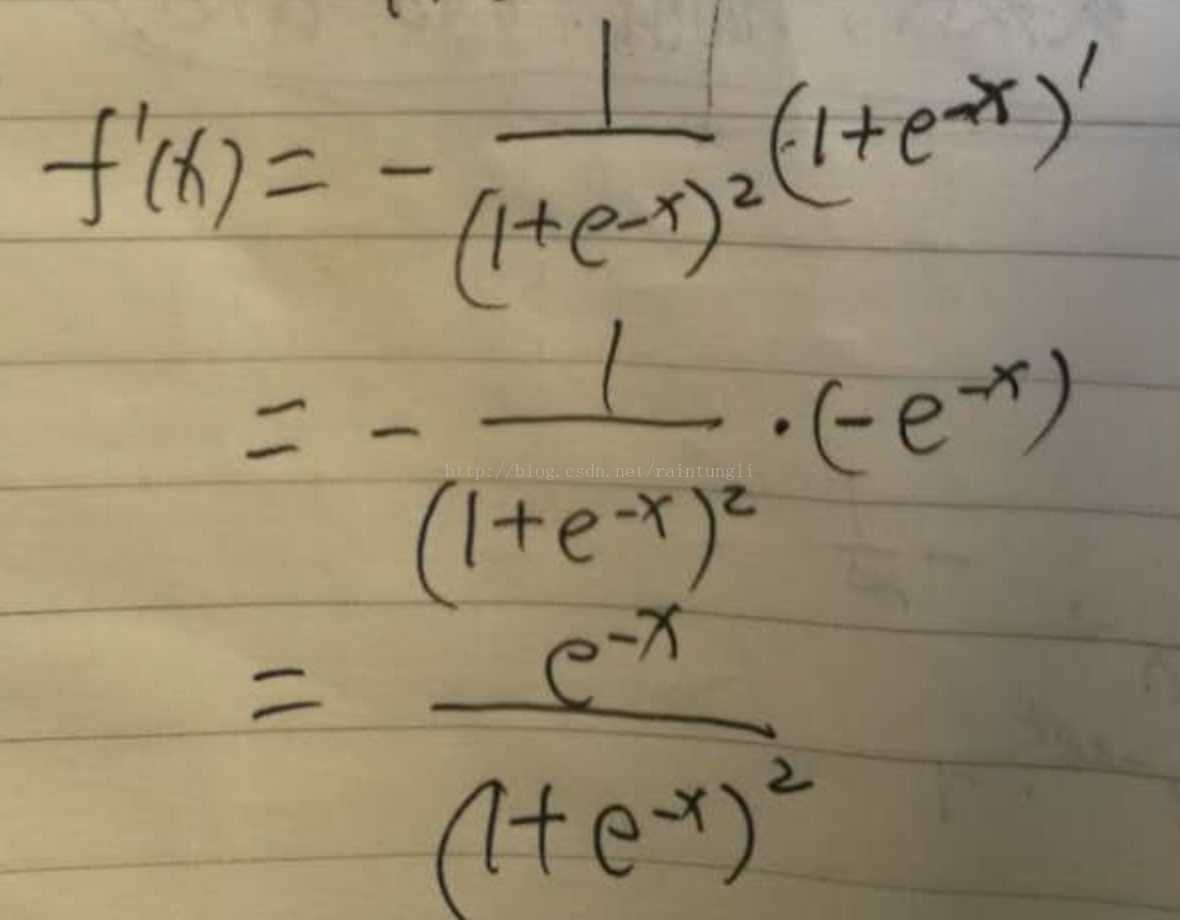
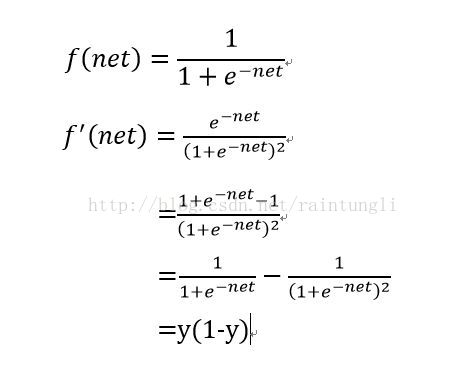
最后推导的结果：

=0.748598311*(1-0.748598311)=0.251401689*0.748598311=0.18819888

• 计算

也就是 net(o1)'=out(h2)=0.601327636

最后我们的公式

= *out(h2)

= 0.248598311*0.18819888*0.601327636=0.028133669

2.3.1.1 跟新W6的权重

W6=W6-x*

其中 x 就是我们常说的学习速率，设置x学习速率为0.1 那么新的w6的权重就是

0.35-0.1* 0.028133669=0.347186633

相同的道理，我们也可以计算新的W5,W6,W7,W8的权重

可是如何计算和跟新W1,W2,W3,W4的权重呢？

2.3.2 隐含层的权值跟新

大概的算法还是和前面类似，如下图所展示：

计算公式：

2.3.2.1 计算

对Out(h1)来说Etotal并不依赖于Out(h1)计算，需要将Total分拆成两个Eo1和Eo2来计算

公式如下：

接着推导公式：

• 计算

• 同理也可以计算

2.3.2.2 计算

2.3.2.3 计算

最后三者相乘：

2.3.2.4 整体公式

根据前面的公式，我们可以推导出最后的公式

2.3.2.4 跟新W1的权重

和计算W6的权重一样：

设置学习速率，计算的到w1的权重值

3. 计算获取最佳的权重

我们将获取的新的权重不停的迭代，迭代一定的次数后直到接近期望值 o1:0.5 o2:0.9后，所的到权重w1...w8，就是所需要的权重。