反向传播算法（过程及公式推导）

        反向传播算法（Backpropagation）是目前用来训练人工神经网络（Artificial Neural Network，ANN）的最常用且最有效的算法。其主要思想是：

（1）将训练集数据输入到ANN的输入层，经过隐藏层，最后达到输出层并输出结果，这是ANN的前向传播过程；

（2）由于ANN的输出结果与实际结果有误差，则计算估计值与实际值之间的误差，并将该误差从输出层向隐藏层反向传播，直至传播到输入层；

（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。

        反向传播算法的思想比较容易理解，但具体的公式则要一步步推导，因此本文着重介绍公式的推导过程。

1. 变量定义

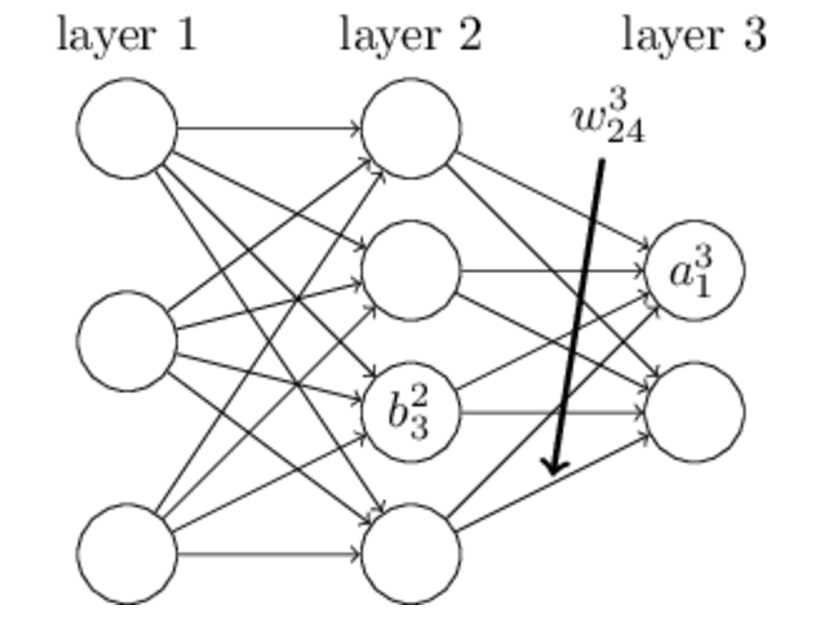
        上图是一个三层人工神经网络，layer1至layer3分别是输入层、隐藏层和输出层。如图，先定义一些变量：

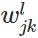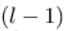
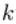        表示第层的第个神经元连接到第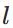层的第个神经元的权重；

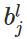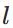        表示第层的第个神经元的偏置；