耶鲁大学 博弈论(Game Theory) 笔记4-足球比赛与商业合作之最佳对策

耶鲁大学 博弈论(Game Theory) 笔记4-足球比赛与商业合作之最佳对策

点球博弈

其中$U_1(4,-4)$=4，即为我选择左路射门而对手选择左路防守时进球概率为40%。
由图可见，选择M永远不是一个最佳对策(BR)

结论

不要选择在任何条件下都非最佳对策的策略。

最佳对策定义

参与者针对对手策略的定义

如果对$S_i$的所有$s{‘}_i$有
$$U_i({\hat{s}}_i,s_{-i})\ge U_i(s_i^{\prime },s_{-i})$$

则参与者$i$的策略${\hat{s}}_i$是对其他参与者策略$s_{-i}$的BR。
或者表示为如下形式，即最大化对手选择策略$s_{-1}$时我方的收益。
$${\hat{s}}_{i}solve{s}_{s_i}^{max}{U}_i(s_i,s_{-1})$$

广义定义

扩展为广义定义后，参与者$i$的策略${\hat{s}}_i$是对其他参与者策略选择持信念P的BR。在参与者持信念 P 的情况下选${\hat{s}}_i$获得的预期收益比在同样的信念p 下选其它策略，获得的预期收益都要高，对于可选的$s_i^{\prime }$均成立。
$$E{U}_i({\hat{s}}_i,P)\ge EU(s_i,P)$$
或表达为如下形式
$${\hat{s}}_{i}solve{s}_{s_i}^{max}E{U}_i(s_i^{\prime },s_{-1})$$
预期收益=我的收益1x对面选择1的概率+我的收益2x对面选择2的概率。

预期收益，此案例中，在参与人 i 持有信念P的情况下，他选择左路攻门的预期收益等于，门将扑向左路的概率乘以两人都选择左路下参与人 i 的收益，再加上门将扑向右路的概率乘以门将扑向右路参与人 i 左路进攻时，参与人 i 的收益，即
$$EU(L,P)=P(l)\times U_1(L,l)+P(r)\times U_1(L,r)$$

合伙人博弈

1.两个参与人都是公司股东，各持有公司 50%的股份，供应合伙关系；

2.每个股东要选择对公司投入精力，以“小时”表示，策略集合 Si=[0,4]，这是一个连续区间，不是同于选数游戏中的只能选整数。

3.利润计算方式如下
$$4\times [s_1+s_2+b\ast s_1\ast s_2]0\le b\le \frac{1}{4}$$

其中b为协同或互补部分。

由此我们可以进行收益计算：
$$\begin{gathered} U_1(s_1,s_2)=\frac{1}{2}[4\times [s_1+s_2+b\ast s_1\ast s_2]]-s_1^2 \\ {U}_2(s_1,s_2)=\frac{1}{2}[4\times [s_1+s_2+b\ast s_1\ast s_2]]-s_2^2 \end{gathered}$$
其中$\frac{1}{2}$为股份占比，$s_1^2$为自身投入。

若要计算选$s_1$时的最大收益($s_2$为已知数)：
$$MA{X}_{s_1}2(s_1+s_2+b\ast s_1\ast s_2)-s_1^2$$
进行求导
$$\begin{gathered} 2(1+b\ast s_2)-2\widehat{s_1}=0 \\ \widehat{s_1}=1+b\ast s_2=BR(s_2) \\ 同理 \\ \widehat{s_2}=1+b\ast s_1=BR(s_1) \end{gathered}$$
此时令导数得零取得最值，再求二阶导判断最大最小，小于零，取得是最大值。
$$0-2\le 0$$

由$BR(s_1)$和$BR(s_2)$可得：
$$B{R}_1(s_2)=1+(\frac{1}{4})s_2$$

将BR用图表示，红色代表参与者1在不同$s_2$下的BR，蓝色为参与者2在不同$s_1$下的BR。

因为永远不要选择劣势策略，因此参与人1的$(0,1)\cup (2,4)$策略被剔除。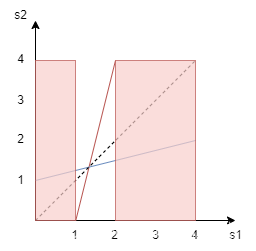
同理，参与人2的$(0,1)\cup (2,4)$策略被剔除，只剩下中间的区域。

将中间区域放大，图像除了点坐标不同外和初始图像完全一样，再次剔除非BR，迭代剔除最终将归为一点。

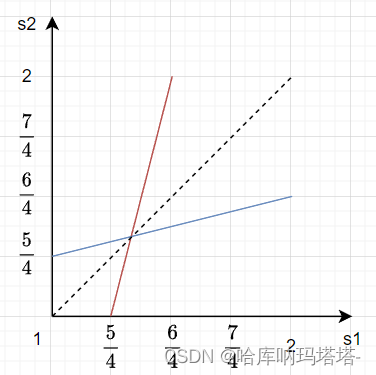
$$\{\begin{array}{r}{s}_1^{\ast }=1+b{s}_2^{\ast }\\ s_2^{\ast }=1+b{s}_1^{\ast }\end{array}\to s_1^{\ast }=s_2^{\ast }=\frac{1}{1-b}$$

外部性

当我计算要为公司付出多少时，没有考虑到利润的一半会归别人所有。

如果减小协同系数b,那么两条线会越来越皆接近于平行和垂直，最终的点会越来越接近于(1,1)。

上图中的交点即是著名的纳什均衡点，在此处双方都采用了自己的最优反应。