LSTM为什么晦涩难懂？Long Short-term Memory 万字解析 论文精读 LSTM的提出

说明：本文是自己阅读Long Short-term Memory期间，发现论文中的公式复杂，于是写了这篇文章进行梳理，同时给出自己的总结方法。
文中的非手绘图片均来自论文Long Short-term Memory。

注意：此篇文章提出的LSTM并不是现在所熟知的LSTM（现在是指2022年），现在的LSTM拥有Forget Gate，但是这篇文章并没有遗忘门，而带遗忘门的LSTM是出自Learning to Forget Continual Prediction with LSTM(LSTM with Forget Gate)，这篇文章发表自1999年，是对Long Short-term Memory的改进。

ABS

文章说明由于梯度爆炸、（特别是）梯度消失的原因，RNN在记录长期记忆，进行反向传播时耗时巨大、效果差。于是提出了LSTM解决这个长期记录的问题。LSTM训练的更快，能够更好的解决复杂问题和长延时(输出依赖两个时间间隔很久的输入)任务。

1 INTRO

现阶段的算法没有很好的解决长延时任务。作者写这篇文章会分析问题和提出一种解决方法。

问题：梯度爆炸、梯度消失。LSTM可以解决长延时任务使用RNN时梯度爆炸和梯度消失的问题。

2 PREVIOUS WORK

这一部分全部在说之前的所有模型存在的问题，目的是为了引出LSTM，此处不做详细介绍。

3 CONSTANT ERROR BACKPROP

这一部分是介绍传统的BPTT（Backpropogation Through Time，这里指的是在RNN上的反向传播）为什么会出现梯度爆炸、梯度消失的问题，同时提出一种解决方法的雏形。

3.1 EXPONENTIALLY DECAYING ERROR

3.1.1 Conventional BPTT

简单介绍了传统的BPTT出现的问题，这一部分的公式写的比较混乱，各种命名也没有说清楚，下面给出另一种方式说明RNN存在的问题。

首先给出一个简单的RNN模型：

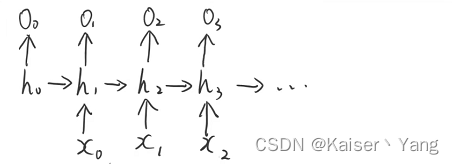
模型中的计算公式如下：

图片中的$\varphi$是一个激活函数。

下面来说明这样一个RNN模型在处理长时间间隔问题时存在的问题，在BPTT中（也就是所谓的反向传播），我们需要计算偏导数，这里我们以更新$W_{xh}$为例，对于$t$时刻我们一共有$t$条反向传播的路径，以t=3为例，存在的路径是：

• $o_3->h_3->x_2$
• $o_3->h_3->h_2>x_1$
• $o_3->h_3->h_2->h_1>x_0$

我们将$x_t$出的权重记作$W_{xh}^{(t)}$（这里不同$x$使用的权重矩阵实际上是同一个）在进行前向传播时有：
$$h_3=W_{hh}{h}_2+W_{xh}{x}_2=W_{hh}(W_{hh}h1+W_{xh}{x}_1)+W_{xh}{x}_2=W_{hh}(W_{hh}(W_{hh}{h}_0+W_{xh}{x}_0)+W_{xh}{x}_1)+W_{xh}{x}_2$$
（为了增加可读性，这里暂时不考虑偏差）
可以看到不同时刻的$x$的系数矩阵出现了相加的情况，根据求导的法则，我们在求导的时候也是相加的关系，此时对于$t$时刻有：

我们将每个时刻的导数根据反向传播的路径展开有：

同时根据$h_t$的计算公式我们可以得到：


（将上式记作equation (2)）。

3.1.2 Outline of Hochreiter’s analysis

对于equation (2)中的红线勾画部分，可以发现：当$t$增加时，图中的指数项的次数会在$k=0$的时候得到最大值：$t-1$，即距离当前位置越远，对应的导数项的指数的次数越大。

3.1.3 Intuitive explanation of equation (2)

equation (2)表明了两种特殊情况：

• ${\varphi }^{\prime }{w}_{hh}>1.0$，容易出现梯度爆炸（梯度随着$t$的增长指数级别增长）
• ${\varphi }^{\prime }{w}_{hh}<1.0$，容易出现梯度消失（梯度随着$t$