统计学习方法--逻辑斯谛回归与最大熵模型（下）

与公众号同步更新，详细内容及相关ipynb文件在公众号中，公众号：AI入门小白

模型学习的最优化算法

逻辑斯谛回归模型、最大熵模型学习归结为以似然函数为目标函数的最优化问题，通常通过迭代算法求解。从最优化的观点看，这时的目标函数具有很好的性质。它是光滑的凸函数，因此多种最优化的方法都适用，保证能找到全局最优解。常用的方法有改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法。牛顿法或拟牛顿法一般收敛速度更快。

下面介绍基于改进的迭代尺度法与拟牛顿法的最大熵模型学习算法。

改进的迭代尺度法

改进的迭代尺度法(improved iterative scaling, IIS) 是一种最大熵模型学习的最优化算法。

己知最大熵模型为
$$P_{\omega }(y|x)=\frac{1}{Z_{\omega }(x)}exp(\sum _{i=1}^n{\omega }_i{f}_i(x,y))$$
其中，
$$Z_{\omega }(x)=\sum _{y}exp(\sum _{i=1}^n{\omega }_i{f}_i(x,y))$$
对数似然函数为
$$L(\omega )=\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\omega }_i{f}_i(x,y)-\sum _x\tilde{P}(x)\log Z_{\omega }(x)$$
目标是通过极大似然估计学习模型参数， 即求对数似然函数的极大值$\hat{\omega }$。

IIS的想法是：假设最大熵模型当前的参数向量是$\omega =({\omega }_1,{\omega }_2,\cdots ,{\omega }_n{)}^T$，我们希望找到一个新的参数向量$\omega +\delta =({\omega }_1+{\delta }_1,{\omega }_2+{\delta }_2,\cdots ,{\omega }_n+{\delta }_n{)}^T$，使得模型的对数似然函数值增大。如果能有这样一种参数向量更新的方法$\tau :\omega \to \omega +\delta$，那么就可以重复使用这一方法，直至找到对数似然函数的最大值。

对于给定的经验分布$\tilde{P}(x,y)$，模型参数从$\omega$到$\omega +\delta$，对数似然函数的改变量是
$$\begin{array}{rl}L(\omega +\delta )-L(\omega )& =\sum _{x,y}\tilde{P}(x,y)\log P_{\omega +\delta }(y|x)-\sum _{x,y}\tilde{P}(x,y)\log P_{\omega }(y|x)\\ & =\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)-\sum _x\tilde{P}(x)\log \frac{Z_{\omega +\delta }(x)}{Z_{\omega }(x)}\end{array}$$
利用不等式
$$-\log \alpha \ge 1-\alpha ,\alpha >0$$
建立对数似然函数改变量的下界：
$$\begin{array}{rl}L(\omega +\delta )-L(\omega )& \ge \sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\sum _x\tilde{P}(x)\frac{Z_{\omega +\delta }(x)}{Z_{\omega }(x)}\\ & =\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\sum _x\tilde{P}(x)\sum _y{P}_{\omega }(y|x)exp\sum _{i=1}^n{\delta }_i{f}_i(x,y)\end{array}$$
将右端记为
$$A(\delta |\omega )=\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\sum _x\tilde{P}(x)\sum _y{P}_{\omega }(y|x)exp\sum _{i=1}^n{\delta }_i{f}_i(x,y)$$
于是有
$$L(\omega +\delta )-L(\omega )\ge A(\delta |\omega )$$
即$A(\delta |\omega )$是对数似然函数改变量的一个下界。

如果能找到适当的$\delta$使下界$A(\delta |\omega )$提高，那么对数似然函数也会提高。然而，函数$A(\delta |\omega )$中的$\delta$是一个向量，含有多个变量，不易同时优化。IIS试图一次只优化其中一个变量${\delta }_i$，而固定其他变量${\delta }_j,i\ne j$。

为达到这一目的，IIS进一步降低下界$A(\delta |\omega )$。具体地，IIS引进一个量$f^{\#}(x,y)$，
$$f^{\#}(x,y)=\sum _i{f}_i(x,y)$$
因为$f_i$是二值函数，故$f^{\#}(x,y)$表示所有特征在$(x,y)$出现的次数。这样，$A(\delta |\omega )$可以改写为
$$\begin{array}{rl}A(\delta |\omega )& =\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\\ & \sum _x\tilde{P}(x)\sum _y{P}_{\omega }(y|x)exp(f^{\#}(x,y)\sum _{i=1}^n\frac{{\delta }_i{f}_i(x,y)}{f^{\#}(x,y)})\end{array}\text{\hspace{1em}(6.30)}$$
利用指数函数的凸性以及对任意$i$，有$\frac{f_i(x,y)}{f^{\#}(x,y)}\ge 0$且${\sum }_{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}=1$这一事实，根据Jensen不等式，得到
$$exp(\sum _{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}{\delta }_i{f}^{\#}(x,y))\le \sum _{i=1}^n\frac{f_i(x,y)}{f^{\#}(x,y)}exp({\delta }_i{f}^{\#}(x,y))$$
于是式(6.30)可改写为
$$\begin{array}{rl}A(\delta |\omega )& \ge \sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\\ & \sum _x\tilde{P}(x)\sum _y{P}_{\omega }(y|x)\sum _{i=1}^n(\frac{f_i(x,y)}{f^{\#}(x,y)})exp({\delta }_i{f}^{\#}(x,y))\end{array}\text{\hspace{1em}(6.31)}$$
记不等式(6.31)右端为
$$B(\delta |\omega )=\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\delta }_i{f}_i(x,y)+1-\sum _x\tilde{P}(x)\sum _y{P}_{\omega }(y|x)\sum _{i=1}^n\left(\frac{f_i(x,y)}{f^{\#}(x,y)}\right)exp({\delta }_i{f}^{\#}(x,y))$$
于是得到
$$L(\omega +\delta )-L(\omega )\ge B(\delta |\omega )$$
这里，$B(\delta |\omega )$是对数似然函数改变量的一个新的(相对不紧的)下界。

求$B(\delta |\omega )$对${\delta }_i$的偏导数：
$$\frac{\partial B(\delta |\omega )}{\partial {\delta }_i}=\sum _{x,y}\tilde{P}(x,y)f_i(x,y)-\sum _x\tilde{P}(x)\sum _y{P}_{\omega }(y|x)f_i(x,y)exp({\delta }_i{f}^{\#}(x,y))\text{\hspace{1em}(6.32)}$$
在式(6.32)里，除${\delta }_i$外不含任何其他变量。令偏导数为0得到
$$\sum _{x,y}\tilde{P}(x)P_{\omega }(y|x)f_i(x,y)exp({\delta }_i{f}^{\#}(x,y))=E_{\tilde{P}}(f_i)\text{\hspace{1em}(6.33)}$$
于是，依次对${\delta }_i$求解方程(6.33)可以求出$\delta$。

这就给出了一种求$\omega$的最优解的迭代算法，即改进的迭代尺度算法IIS。

算法6.1(改进的迭代尺度算法IIS)
输入：特征函数$f_1,f_2,\cdots ,f_n$；经验分布$\tilde{P}(X,Y)$，模型$P_{\omega }(y|x)$；
输出：最优参数值${\omega }_i^{\ast }$；最优模型$P_{{\omega }^{\ast }}$。
(1)对所有 i ∈ { 1 , 2 , ⋯   , n } i \in \{1,2,\cdots,n\} i∈{1,2,⋯,n}，取初值${\omega }_i=0$。
(2)对每一 i ∈ { 1 , 2 , ⋯   , n } i \in \{1,2,\cdots,n \} i∈{1,2,⋯,n}

• (a)令${\delta }_i$是方程
  $$\sum _{x,y}\tilde{P}(x)P(y|x)f_i(x,y)exp({\delta }_i{f}^{\#}(x,y))=E_{\tilde{P}}(f_i)$$
  的解，这里，
  $$f^{\#}(x,y)=\sum _{i=1}^n{f}_i(x,y)$$
• (b)更新${\omega }_i$值：${\omega }_i\leftarrow {\omega }_i+{\delta }_i$。

(3)如果不是所有${\omega }_i$都收敛，重复步(2)。

这一算法关键的一步是(a)，即求解方程(6.33)中的${\delta }_i$。如果$f^{\#}(x,y)$是常数，即对任何$x,y$，有$f^{\#}(x,y)=M$，那么${\delta }_i$可以显式地表示成
$${\delta }_i=\frac{1}{M}\log \frac{E_{\tilde{P}}(f_i)}{E_P(f_i)}\text{\hspace{1em}(6.34)}$$
如果$f^{\#}(x,y)$不是常数，那么必须通过数值计算求${\delta }_i$。简单有效的方法是牛顿法。

以$g({\delta }_i)=0$表示方程(6.33)，牛顿法通过迭代求得${\delta }_i^{\ast }$，使得$g({\delta }_i^{\ast })=0$。迭代公式是
$${\delta }_i^{(k+1)}={\delta }_i^{(k)}-\frac{g({\delta }_i^{(k)})}{g^{\prime }({\delta }_i^{(k)})}\text{\hspace{1em}(6.35)}$$
只要适当选取初始值${\delta }_i^{(0)}$，由于${\delta }_i$的方程(6.33)有单根，因此牛顿法恒收敛，而且收敛速度很快。

拟牛顿法

最大熵模型学习还可以应用牛顿法或拟牛顿法。

对于最大熵模型而言，
$$P_{\omega }(y|x)=\frac{exp({\sum }_{i=1}^n{\omega }_i{f}_i(x,y))}{{\sum }_{y}exp({\sum }_{i=1}^n{\omega }_i{f}_i(x,y))}$$
目标函数：
$$\underset{\omega \in R^n}{\min }f(\omega )=\sum _x\tilde{P}(x)\log \sum _{y}exp(\sum _{i=1}^n{\omega }_i{f}_i(x,y))-\sum _{x,y}\tilde{P}(x,y)\sum _{i=1}^n{\omega }_i{f}_i(x,y)$$
梯度：
$$g(\omega )=(\frac{\partial f(\omega )}{\partial {\omega }_1},\frac{\partial f(\omega )}{\partial {\omega }_2},\cdots ,\frac{\partial f(\omega )}{\partial {\omega }_n}{)}^T$$
其中
$$\frac{\partial f(\omega )}{\partial {\omega }_i}=\sum _{x,y}\tilde{P}(x)P_{\omega }(y|x)f_i(x,y)-E_{\tilde{P}}(f_i),i=1,2,\cdots ,n$$
相应的拟牛顿法BFGS 算法如下。

算法6.2(最大熵模型学习的BFGS 算法)
输入：特征函数$f_1,f_2,\cdots ,f_n$；经验分布$\tilde{P}(x,y)$，目标函数$f(\omega )$，梯度$g(\omega )=\nabla f(\omega )$，精度要求$\epsilon$；
输出：最优参数值${\omega }^{\ast }$；最优模型$P_{{\omega }^{\ast }}(y|x)$。
(1)选定初始点${\omega }^{(0)}$，取$B_0$为正定对称矩阵，置$k=0$；
(2)计算$g_k=g({\omega }^{(k)})$。若$\Vert g_k\Vert <\epsilon$，则停止计算， 得${\omega }^{\ast }={\omega }^{(k)}$；否则转(3)；
(3)由$B_k{p}_k=-g_k$求出$p_k$；
(4)一维搜索：求${\lambda }_k$使得
$$f({\omega }^{(k)}+{\lambda }_k{p}_k)=\underset{\lambda \ge 0}{\min }f({\omega }^{(k)}+\lambda p_k)$$
(5)置${\omega }^{(k+1)}={\omega }^{(k)}+{\lambda }_k{p}_k$；
(6)计算$g_{k+1}=g({\omega }^{(k+1)})$，若$\Vert g_{k+1}\Vert <\epsilon$，则停止计算，得${\omega }^{\ast }={\omega }^{(k+1)}$；否则，按下式求出$B_{k+1}$：
$$B_{k+1}=B_k+\frac{y_k{y}_k^T}{y_k^T{\delta }_k}-\frac{B_k{\delta }_k{\delta }_k^T{B}_k}{{\delta }_k^T{B}_k{\delta }_k}$$
其中，
$$y_k=g_{k+1}-g_k,{\delta }_k={\omega }^{(k+1)}-{\omega }^{(k)}$$
(7)置$k=k+1$，转(3)。

代码部分

from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# data
def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0,1,-1]])
    # print(data)
    return data[:,:2], data[:,-1]

X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

'''
np.mat()函数用于将输入解释为矩阵。
np.matrix()函数用于从类数组对象或数据字符串返回矩阵。
np.array()函数用于创建一个数组。
'''
class LogisticReressionClassifier:
    def __init__(self, max_iter=200, learning_rate=0.01):
        self.max_iter = max_iter   # 迭代次数
        self.learning_rate = learning_rate
        
    def sigmoid(self, x):
        return 1 / (1 + exp(-x))  
    
    def data_matrix(self, X):
        data_mat = []
        for d in X:
            data_mat.append([1.0, *d])
        return data_mat
    
    def fit(self, X, y):
        # label = np.mat(y)  # https://blog.csdn.net/yeler082/article/details/90342438
        data_mat = self.data_matrix(X) # m*n  ([1.0,X_1],[1.0,X_2],...)
        self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)
        
        for iter_ in range(self.max_iter):
            for i in range(len(X)):
                result = self.sigmoid(np.dot(data_mat[i], self.weights))  # sigmoid(x * w)
                error = y[i] - result  # 结果若不为0，则分类错误
                self.weights += self.learning_rate * error * np.transpose(
                    [data_mat[i]])  # 更新权值 w，分类若正确,error=0，权值不变
        print('LogisticRegression Model(learning_rate={},max_iter={})'.format(
            self.learning_rate, self.max_iter))
        
    #def f(self, x):
    #    return -(self.weights[0] + self.weights[1] * x) / self.weights[2]
    
    def score(self, X_test, y_test):
        right = 0
        X_test = self.data_matrix(X_test)
        for x, y in zip(X_test, y_test):
            result = np.dot(x, self.weights)
            if (result > 0 and y == 1) or (result < 0 and y == 0):
                right += 1
        return right / len(X_test)

lr_clf = LogisticReressionClassifier()
lr_clf.fit(X_train, y_train)

lr_clf.score(X_test, y_test)

x_ponits = np.arange(4, 8)
y_ = -(lr_clf.weights[1] * x_ponits + lr_clf.weights[0]) / lr_clf.weights[2]
plt.plot(x_ponits, y_)
plt.tick_params(axis='x', colors='white') 
plt.tick_params(axis='y', colors='white') 

# lr_clf.show.graph()
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()

scikit-learn实例

sklearn.linear_model.LogisticRegression

solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是：

• a) liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
• b) lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
• c) newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
• d) sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(max_iter=200) # https://blog.csdn.net/jark_/article/details/78342644
clf.fit(X_train, y_train)

clf.score(X_test, y_test)

# https://www.jianshu.com/p/6a818b53a37e
# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html?highlight=logisticregression%20coef_
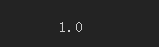
print(clf.coef_, clf.intercept_)  

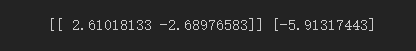
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)
plt.tick_params(axis='x', colors='white') 
plt.tick_params(axis='y', colors='white') 

plt.plot(X[:50, 0], X[:50, 1], 'bo', color='blue', label='0')
plt.plot(X[50:, 0], X[50:, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length', color='white')
plt.ylabel('sepal width', color='white')
plt.legend()

最大熵模型

import math
from copy import deepcopy

class MaxEntropy:
    def __init__(self, EPS=0.005):
        self._samples = []
        self._Y = set()  # 标签集合，相当去去重后的y
        self._numXY = {}  # key为(x,y)，value为出现次数
        self._N = 0  # 样本数
        self._Ep_ = []  # 样本分布的特征期望值
        self._xyID = {}  # key记录(x,y),value记录id号
        self._n = 0  # 特征键值(x,y)的个数
        self._C = 0  # 最大特征数
        self._IDxy = {}  # key为(x,y)，value为对应的id号
        self._w = []
        self._EPS = EPS  # 收敛条件
        self._lastw = []  # 上一次w参数值

    def loadData(self, dataset):
        self._samples = deepcopy(dataset)
        for items in self._samples:
            y = items[0]
            X = items[1:]
            self._Y.add(y)  # 集合中y若已存在则会自动忽略
            for x in X:
                if (x, y) in self._numXY:
                    self._numXY[(x, y)] += 1
                else:
                    self._numXY[(x, y)] = 1

        self._N = len(self._samples)
        self._n = len(self._numXY)
        self._C = max([len(sample) - 1 for sample in self._samples])
        self._w = [0] * self._n    # self._n个0
        self._lastw = self._w[:]

        self._Ep_ = [0] * self._n
        # enumerate() 函数用于将一个可遍历的数据对象组合为一个索引序列，同时列出数据和数据下标
        for i, xy in enumerate(self._numXY):  # 计算特征函数fi关于经验分布的期望
            self._Ep_[i] = self._numXY[xy] / self._N  # 出现次数 / 总数
            self._xyID[xy] = i
            self._IDxy[i] = xy

    def _Zx(self, X):  # 计算每个Z(x)值
        zx = 0
        for y in self._Y:
            ss = 0
            for x in X:
                if (x, y) in self._numXY:
                    ss += self._w[self._xyID[(x, y)]]
            zx += math.exp(ss)  # 式6.23
        return zx

    def _model_pyx(self, y, X):  # 计算每个P(y|x)
        zx = self._Zx(X)
        ss = 0
        for x in X:
            if (x, y) in self._numXY:
                ss += self._w[self._xyID[(x, y)]]
        pyx = math.exp(ss) / zx  # 式6.22
        return pyx

    def _model_ep(self, index):  # 计算特征函数fi关于模型的期望
        x, y = self._IDxy[index]
        ep = 0
        for sample in self._samples:
            if x not in sample:
                continue
            pyx = self._model_pyx(y, sample)
            ep += pyx / self._N  # 一共循环了x频数的次数
        return ep

    def _convergence(self):  # 判断是否全部收敛
        for last, now in zip(self._lastw, self._w):
            if abs(last - now) >= self._EPS:
                return False
        return True

    def predict(self, X):  # 计算预测概率
        Z = self._Zx(X)
        result = {}
        for y in self._Y:
            ss = 0
            for x in X:
                if (x, y) in self._numXY:
                    ss += self._w[self._xyID[(x, y)]]
            pyx = math.exp(ss) / Z
            result[y] = pyx
        return result

    def train(self, maxiter=1000):  # 训练数据
        for loop in range(maxiter):  # 最大训练次数
            print("iter:%d" % loop)
            self._lastw = self._w[:]
            for i in range(self._n):
                ep = self._model_ep(i)  # 计算第i个特征的模型期望
                self._w[i] += math.log(self._Ep_[i] / ep) / self._C  # 更新参数,IIS算法,式6.34
            print("w:", self._w)
            if self._convergence():  # 判断是否收敛
                break

dataset = [['no', 'sunny', 'hot', 'high', 'FALSE'],
           ['no', 'sunny', 'hot', 'high', 'TRUE'],
           ['yes', 'overcast', 'hot', 'high', 'FALSE'],
           ['yes', 'rainy', 'mild', 'high', 'FALSE'],
           ['yes', 'rainy', 'cool', 'normal', 'FALSE'],
           ['no', 'rainy', 'cool', 'normal', 'TRUE'],
           ['yes', 'overcast', 'cool', 'normal', 'TRUE'],
           ['no', 'sunny', 'mild', 'high', 'FALSE'],
           ['yes', 'sunny', 'cool', 'normal', 'FALSE'],
           ['yes', 'rainy', 'mild', 'normal', 'FALSE'],
           ['yes', 'sunny', 'mild', 'normal', 'TRUE'],
           ['yes', 'overcast', 'mild', 'high', 'TRUE'],
           ['yes', 'overcast', 'hot', 'normal', 'FALSE'],
           ['no', 'rainy', 'mild', 'high', 'TRUE']]

maxent = MaxEntropy()
x = ['overcast', 'mild', 'high', 'FALSE']

maxent.loadData(dataset)
maxent.train()

print('predict:', maxent.predict(x))

第6章Logistic回归与最大熵模型-习题

习题6.1

  确认Logistic分布属于指数分布族。

解答：
第1步：
首先给出指数分布族的定义：
对于随机变量$x$，在给定参数$\eta$下，其概率分别满足如下形式：$$p(x|\eta )=h(x)g(\eta )\exp ({\eta }^{T}u(x))$$我们称之为指数分布族。
其中：
$x$：可以是标量或者向量，可以是离散值也可以是连续值
$\eta$：自然参数
$g(\eta )$：归一化系数
$h(x),u(x)$：$x$的某个函数

---

第2步： 证明伯努利分布属于指数分布族
伯努利分布：$\phi$是$y=1$的概率，即$P(Y=1)=\phi$
$\begin{array}{rl}P(y|\phi )& ={\phi }^y(1-\phi {)}^{(1-y)}\\ & =(1-\phi ){\phi }^y(1-\phi {)}^{(-y)}\\ & =(1-\phi )(\frac{\phi }{1-\phi }{)}^y\\ & =(1-\phi )\exp \left(y\ln \frac{\phi }{1-\phi }\right)\\ & =\frac{1}{1+e^{\eta }}\exp (\eta y)\end{array}$
其中，$\eta =\ln \frac{\phi }{1-\phi }\iff \phi =\frac{1}{1+e^{-\eta }}$
将$y$替换成$x$，可得$P(x|\eta )=\frac{1}{1+e^{\eta }}\exp (\eta x)$
对比可知，伯努利分布属于指数分布族，其中$h(x)=1,g(\eta )=\frac{1}{1+e^{\eta }},u(x)=x$

---

第3步：
广义线性模型（GLM）必须满足三个假设：

1. $y|x;\theta \sim ExponentialFamily(\eta )$，即假设预测变量$y$在给定$x$，以$\theta$为参数的条件概率下，属于以$\eta$作为自然参数的指数分布族；
2. 给定$x$，求解出以$x$为条件的$T(y)$的期望$E[T(y)|x]$，即算法输出为$h(x)=E[T(y)|x]$
3. 满足$\eta ={\theta }^{T}x$，即自然参数和输入特征向量$x$之间线性相关，关系由$\theta$决定，仅当$\eta$是实数时才有意义，若$\eta$是一个向量，则${\eta }_i={\theta }_i^{T}x$

---

第4步： 推导伯努利分布的GLM
已知伯努利分布属于指数分布族，对给定的$x,\eta$，求解期望：$$\begin{array}{rl}{h}_{\theta }(x)& =E[y|x;\theta ]\\ & =1\cdot p(y=1)+0\cdot p(y=0)\\ & =\phi \\ & =\frac{1}{1+e^{-\eta }}\\ & =\frac{1}{1+e^{-{\theta }^{T}x}}\end{array}$$可得到Logistic回归算法，故Logistic分布属于指数分布族，得证。

习题6.2

  写出Logistic回归模型学习的梯度下降算法。
解答：
对于Logistic模型：$$\begin{gathered} P(Y=1|x)=\frac{\exp (w\cdot x+b)}{1+\exp (w\cdot x+b)} \\ P(Y=0|x)=\frac{1}{1+\exp (w\cdot x+b)} \end{gathered}$$对数似然函数为：$L(w)=\sum _{i=1}^N\left[y_i(w\cdot x_i)-\log \left(1+\exp (w\cdot x_i)\right)\right]$
似然函数求偏导，可得
$\frac{\partial L(w)}{\partial w^{(j)}}=\sum _{i=1}^N\left[x_i^{(j)}\cdot y_i-\frac{\exp (w\cdot x_i)\cdot x_i^{(j)}}{1+\exp (w\cdot x_i)}\right]$
梯度函数为：$\nabla L(w)=\left[\frac{\partial L(w)}{\partial w^{(0)}},\cdots ,\frac{\partial L(w)}{\partial w^{(m)}}\right]$
Logistic回归模型学习的梯度下降算法：
(1) 取初始值$x^{(0)}\in R$，置$k=0$
(2) 计算$f(x^{(k)})$
(3) 计算梯度$g_k=g(x^{(k)})$，当$\Vert g_k\Vert <\epsilon$时，停止迭代，令$x^{\ast }=x^{(k)}$；否则，求${\lambda }_k$，使得$f(x^{(k)}+{\lambda }_k{g}_k)=\underset{\lambda ⩾0}{\max }f(x^{(k)}+\lambda g_k)$
(4) 置$x^{(k+1)}=x^{(k)}+{\lambda }_k{g}_k$，计算$f(x^{(k+1)})$，当$\Vert f(x^{(k+1)})-f(x^{(k)})\Vert <\epsilon$或 $\Vert x^{(k+1)}-x^{(k)}\Vert <\epsilon$时，停止迭代，令$x^{\ast }=x^{(k+1)}$
(5) 否则，置$k=k+1$，转(3)

%matplotlib inline
import numpy as np
import time
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from pylab import mpl

# 图像显示中文
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']


class LogisticRegression:
    def __init__(self, learn_rate=0.1, max_iter=10000, tol=1e-2):
        self.learn_rate = learn_rate  # 学习率
        self.max_iter = max_iter  # 迭代次数
        self.tol = tol  # 迭代停止阈值
        self.w = None  # 权重

    def preprocessing(self, X):
        """将原始X末尾加上一列，该列数值全部为1"""
        row = X.shape[0]  # 0:输出行数，1:输出列数
        y = np.ones(row).reshape(row, 1)
        X_prepro = np.hstack((X, y))  # https://blog.csdn.net/m0_37393514/article/details/79538748
        return X_prepro

    def sigmod(self, x):
        return 1 / (1 + np.exp(-x))

    def fit(self, X_train, y_train):
        X = self.preprocessing(X_train)
        y = y_train.T
        # 初始化权重w
        self.w = np.array([[0] * X.shape[1]], dtype=np.float)
        k = 0
        for loop in range(self.max_iter):
            # 计算梯度
            z = np.dot(X, self.w.T)
            grad = X * (y - self.sigmod(z))
            grad = grad.sum(axis=0)
            # 利用梯度的绝对值作为迭代中止的条件
            # all() 函数用于判断给定的可迭代参数中的所有元素是否都为TRUE，如果是返回True，否则返回False。
            if (np.abs(grad) <= self.tol).all():
                break
            else:
                # 更新权重w 梯度上升——求极大值
                self.w += self.learn_rate * grad
                k += 1
        print("迭代次数：{}次".format(k))
        print("最终梯度：{}".format(grad))
        print("最终权重：{}".format(self.w[0]))

    def predict(self, x):
        p = self.sigmod(np.dot(self.preprocessing(x), self.w.T))
        print("Y=1的概率被估计为：{:.2%}".format(p[0][0]))  # 调用score时，注释掉
        p[np.where(p > 0.5)] = 1  # https://blog.csdn.net/island1995/article/details/90200151
        p[np.where(p < 0.5)] = 0
        return p

    def score(self, X, y):
        y_c = self.predict(X)
        error_rate = np.sum(np.abs(y_c - y.T)) / y_c.shape[0]
        return 1 - error_rate

    def draw(self, X, y):
        # 分离正负实例点
        y = y[0]
        X_po = X[np.where(y == 1)]
        X_ne = X[np.where(y == 0)]
        # 绘制数据集散点图
        ax = plt.axes(projection='3d')
        x_1 = X_po[0, :]
        y_1 = X_po[1, :]
        z_1 = X_po[2, :]
        x_2 = X_ne[0, :]
        y_2 = X_ne[1, :]
        z_2 = X_ne[2, :]
        ax.scatter(x_1, y_1, z_1, c="r", label="正实例")
        ax.scatter(x_2, y_2, z_2, c="b", label="负实例")
        ax.legend(loc='best')
        # 绘制p=0.5的区分平面
        x = np.linspace(-3, 3, 3)
        y = np.linspace(-3, 3, 3)
        x_3, y_3 = np.meshgrid(x, y)
        a, b, c, d = self.w[0]
        z_3 = -(a * x_3 + b * y_3 + d) / c
        ax.plot_surface(x_3, y_3, z_3, alpha=0.5)  # 调节透明度
        plt.show()

# 训练数据集
X_train = np.array([[3, 3, 3], [4, 3, 2], [2, 1, 2], [1, 1, 1], [-1, 0, 1],
                    [2, -2, 1]])
y_train = np.array([[1, 1, 1, 0, 0, 0]])
# 构建实例，进行训练
clf = LogisticRegression()
clf.fit(X_train, y_train)
clf.draw(X_train, y_train)

习题6.3

  写出最大熵模型学习的DFP算法。
解答：
第1步：
最大熵模型为：$$\begin{array}{cl}\max & H(p)=-{\sum }_{x,y}P(x)P(y|x)\log P(y|x)\\ \text{st.}& E_p(f_i)-E_{\hat{p}}(f_i)=0,i=1,2,\cdots ,n\\ & {\sum }_{y}P(y|x)=1\end{array}$$引入拉格朗日乘子，定义拉格朗日函数：$$\begin{gathered} L(P,w)=\sum _{xy}P(x)P(y|x)\log P(y|x)+w_0\left(1-\sum _{y}P(y|x)\right) \\ +\sum _{i=1}{w}_i\left(\sum _{xy}P(x,y)f_i(x,y)-\sum _{xy}P(x,y)P(y|x)f_i(x,y)\right) \end{gathered}$$
最优化原始问题为：$$\underset{P\in C}{\min }\underset{w}{\max }L(P,w)$$对偶问题为：$$\underset{w}{\max }\underset{P\in C}{\min }L(P,w)$$令$$\Psi (w)=\underset{P\in C}{\min }L(P,w)=L(P_w,w)$$$\Psi (w)$称为对偶函数，同时，其解记作$$P_w={\mathrm{argmin}}_{P\in C}L(P,w)=P_w(y|x)$$求$L(P,w)$对$P(y|x)$的偏导数，并令偏导数等于0，解得：$$P_w(y|x)=\frac{1}{Z_w(x)}\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)$$其中：$$Z_w(x)=\sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)$$则最大熵模型目标函数表示为$$\phi (w)=\underset{w\in R_n}{\min }\Psi (w)=\sum _{x}P(x)\log \sum _y\exp \left(\sum _{i=1}^n{w}_i{f}_i(x,y)\right)-\sum _{x,y}P(x,y)\sum _{i=1}^n{w}_i{f}_i(x,y)$$
第2步：
DFP的$G_{k+1}$的迭代公式为：$$G_{k+1}=G_k+\frac{{\delta }_k{\delta }_k^T}{{\delta }_k^T{y}_k}-\frac{G_k{y}_k{y}_k^T{G}_k}{y_k^T{G}_k{y}_k}$$
最大熵模型的DFP算法：
输入：目标函数$\phi (w)$，梯度$g(w)=\nabla g(w)$，精度要求$\epsilon$；
输出：$\phi (w)$的极小值点$w^{\ast }$
(1)选定初始点$w^{(0)}$，取$G_0$为正定对称矩阵，置$k=0$
(2)计算$g_k=g(w^{(k)})$，若$\Vert g_k\Vert <\epsilon$，则停止计算，得近似解$w^{\ast }=w^{(k)}$，否则转(3)
(3)置$p_k=-G_k{g}_k$
(4)一维搜索：求${\lambda }_k$使得$$\phi \left(w^{(k)}+{\lambda }_k{P}_k\right)=\underset{\lambda ⩾0}{\min }\phi \left(w^{(k)}+\lambda P_k\right)$$(5)置$w^{(k+1)}=w^{(k)}+{\lambda }_k{p}_k$
(6)计算$g_{k+1}=g(w^{(k+1)})$，若$\Vert g_{k+1}\Vert <\epsilon$，则停止计算，得近似解$w^{\ast }=w^{(k+1)}$；否则，按照迭代式算出$G_{k+1}$
(7)置$k=k+1$，转(3)

数据来源：统计学习方法(第二版) &
https://github.com/fengdu78/lihang-code