机器学习笔记十

第十一讲：贝叶斯统计、机器学习应用建议

我们今天将要介绍另一种避免过拟合的方法——正则化，该方法不需要剔除特征值。

3. 贝叶斯统计与正则化

在一开始，我们先来讨论使用最大似然（ML: Maximum Likelihood）拟合参数。以往，我们都是通过下面这个式子选择参数：

$${\theta }_{\mathrm{ML}}=\arg \underset{\theta }{\max }\prod _{i=1}^{m}p\left(y^{(i)}\mid x^{(i)};\theta \right)$$

在后面的讨论中，我们始终将$\theta$看做未知参数。从**频率学派（frequentist）**的观点看，$\theta$是一个未知的但却是常量的值。对于频率派来说，$\theta$并不是随机变量，它是一个参数，只是恰巧不知道它的值而已，而我们的任务就是通过使用一些统计步骤（如最大似然法）来估计这个参数的值。

从贝叶斯学派的观点看问题，则会找到另一种估计参数的方法——他们将$\theta$看做是一个随机变量，其值未知。于是，我们可以假设一个关于$\theta$的先验分布（prior distribution）$p(\theta )$，用来表示我们“相信”参数取值的不确定性。对于给定的训练集$S={\left\{\left(x^{(i)},y^{(i)}\right)\right\}}_{i=1}^m$，当我们需要预测一个新的$x$时，我们就可以计算参数的后验分布：

$$\begin{array}{rl}p(\theta \mid S)& =\frac{p(S\mid \theta )p(\theta )}{p(S)}\\ & =\frac{\left({\prod }_{i=1}^{m}p\left(y^{(i)}\mid x^{(i)},\theta \right)\right)p(\theta )}{{\int }_{\theta }\left({\prod }_{i=1}^{m}p\left(y^{(i)}\mid x^{(i)},\theta \right)p(\theta )\right)\mathrm{d}\theta }\end{array}\text{\hspace{1em}(1)}$$

式中的$p\left(y^{(i)}\mid x^{(i)},\theta \right)$来自我们在学习问题中选择的模型。举个例子，如果我们使用贝叶斯逻辑回归，那么$p\left(y^{(i)}\mid x^{(i)},\theta \right)=h_{\theta }{\left(x^{(i)}\right)}^{y^{(i)}}{\left(1-h_{\theta }\left(x^{(i)}\right)\right)}^{\left(1-y^{(i)}\right)}$，这里的$h_{\theta }\left(x^{(i)}\right)=\frac{1}{1+\exp \left(-{\theta }^T{x}^{(i)}\right)}$。（因为我们已经把$\theta$看做是一个随机变量了，所以就可以把它写入条件概率的条件中，即使用$p(y\mid x;\theta )$代替$p(y\mid x,\theta )$。）

当我们需要预测新的$x$时，就可以使用关于$\theta$的后验分布计算相应标记类型$y$上的后验概率了：

$$p(y\mid x,S)={\int }_{\theta }p(y\mid x,\theta )p(\theta \mid S)\mathrm{d}\theta \text{\hspace{1em}(2)}$$

上式中的$p(\theta \mid S)$来自$(1)$式，举个例子，如果要预测给定$x$的标记类型$y$，则有（如果$y$是取离散值，则使用求和代替求积分）：

$$\mathrm{E}[y\mid x,S]={\int }_{y}yp(y\mid x,S)\mathrm{d}y$$

上面简要的例子可以看做是“完全贝叶斯式的”预测，也就是计算$p(\theta \mid S)$关于$\theta$的后验概率的平均值。不过，这个后验分布通常难以计算，因为在$(1)$中需要求出关于$\theta$（通常是维度很高）的积分，一般难以求得这些积分的闭合形式（即解析解，相对于数值解而言）。

因此，在实践中，我们选择近似这个关于$\theta$的后验分布。一个常用的近似就是使用一个点的估计来代替这个后验分布。介绍一下关于$\theta$的**MAP（maximum a posteriori）**估计（也就是对$\theta$后验概率的最大化估计，因为后验概率正比于$(1)$式的分子，所以我们最大化这个分子）：

$$\begin{array}{rl}{\theta }_{\mathrm{MAP}}& =\arg \underset{\theta }{\max }p(\theta \mid S)\\ & =\arg \underset{\theta }{\max }\prod _{i=1}^{m}p\left(y^{(i)}\mid x^{(i)},\theta \right)p(\theta )\end{array}\text{\hspace{1em}(3)}$$

与关于$\theta$的最大似然估计的式子相比，这个式子只是最后多了一项$p(\theta )$。（对于这个式子的直观理解，参数服从$\theta \sim \mathcal{N}\left(0,{\tau }^{2}I\right)$，这是一个期望为$0$的高斯分布，具有一定的协方差${\tau }^{2}I$，对于这样一个分布，大部分的概率质量都集中在$0$附近。所以这个先验概率的意义就是，多数的参数都应该接近于$0$，回忆上一讲介绍的特征选择，如果我们剔除某个特征，也就等同于将其值置为$0$，这是一个与特征选择类似的过程，虽然它不会将大多数参数严格的置为$0$。我们用最大似然估计拟合参数时，如果是使用高次多项式拟合，那么得到的曲线将会有较大波动，而使用贝叶斯正则化方法时，得到的曲线将随着$\tau$的减小而越来越平滑，因为协方差减小时越来越多的特征值将向$0$靠近。）

（极大似然估计算法，比如线性回归，尝试最小化$\underset{\theta }{\min }\sum _i{\Vert y^{(i)}-{\theta }^T{x}^{(i)}\Vert }^2$。而现在加入先验概率后，相当于最小化$\underset{\theta }{\min }\sum _i{\Vert y^{(i)}-{\theta }^T{x}^{(i)}\Vert }^2+\lambda \Vert \theta {\Vert }^2$，也就是在最后加了一项，当参数过大时会惩罚目标函数。所以，这个算法与极大似然估计相似，但倾向于选择较小的参数，得到的拟合更加平滑。）

在实际应用中，对于先验概率$p(\theta )$来说，通常假设$\theta \sim \mathcal{N}\left(0,{\tau }^{2}I\right)$。与最大似然相比，通过使用先验拟合得到的参数${\theta }_{\mathrm{MAP}}$具有较小的范数（即${\Vert {\theta }_{\mathrm{MAP}}\Vert }^2\le {\Vert {\theta }_{\mathrm{ML}}\Vert }^2$）。在实际应用中，与ML相比，贝叶斯MAP估计更不容易受到过拟合影响。比如，在文本分类问题上即使当$n\gg m$时，贝叶斯逻辑回归也表现出良好的性能。

4. 感知及大间隔分类器

在关于学习理论的讲义的最后，我们来介绍一种不同的机器学习模型。到目前位置，我们介绍的方法都属于**批量学习（batch learning）算法，也就是先使用训练集训练模型，再使用另一个集合中的测试数据来评估得到的的假设函数$h$。那么接下来，我们将介绍在线学习（online learning）**算法，该算法在学习时也需要持续的做出预测。

对于给定的训练样本序列$\left(x^{(1)},y^{(1)}\right),\left(x^{(2)},y^{(2)}\right),\cdots ,\left(x^{(m)},y^{(m)}\right)$，算法先看到$x^{(1)}$，然后要对其做出预测得到${\hat{y}}^{(1)}$，在预测之后，算法才会知道$y^{(1)}$真实值（然后算法可能会根据这个真实值做学习调整）。接着，算法看到$x^{(2)}$，然后要再对这个输入做出预测得到${\hat{y}}^{(2)}$，之后会得到$y^{(2)}$真实值，算法再根据这个真实值做出学习调整。这个过程会一直持续到$\left(x^{(m)},y^{(m)}\right)$。对于在线学习算法，我们关心整个学习过总在线误差（total online error）$\sum _{i=1}^{m}1\left\{{\hat{y}}^{(i)}\ne y^{(i)}\right\}$。因此，这个是一个即使在在学习的过程中也要做出预测的算法。

（其实我们以前的学习算法都可以使用在线学习，比如，在需要对$x^{(3)}$做出预测时，我们将前面的两个样本作为训练集使用即可。而对于某些算法，比如梯度下降法，可以更好的应用在线学习算法。）

我们先给感知算法的在线误差设一个界限。为了简化接下来的推导，我们使用管理标记 y ∈ { − 1 , 1 } y\in\left\{-1,1\right\} y∈{−1,1}。

回忆具有参数$\theta \in {\mathbb{R}}^{n+1}$的感知算法，它按照下面的式子做出预测：

KaTeX parse error: \tag works only in display equations

其中$g(z)=\{\begin{array}{ll}1& \text{if }z\ge 0\\ -1& \text{if }z<0\end{array}$。

对于给定的训练样本$(x,y)$，感知学习算法的更新规则为：

• 如果$h_{\theta }(x)=y$，则参数不更新；
• 否则，按规则$\theta :=\theta +yx$更新。（这与我们最初在第三讲中介绍的更新规则略有不同，因为我们现在使用 y ∈ { − 1 , 1 } y\in\left\{-1,1\right\} y∈{−1,1}作为标记，同时也放弃使用学习速率参数$\alpha$。因为此时的学习速率只会按一个常量同时缩放所有的参数，而对感知算法的学习行为没有任何影响。）

下面的理论将会给感知算法的在线学习误差一个界限，当感知算法按照在线学习算法运行时，每次错误的预测都会引起参数更新。应当注意的是，下面这个理论中关于“误差个数的界限”同“序列中样本的总数$m$”或是“输入特征的维度$n$”并无明确的依赖关系。

**定理（Block, 1962, and Novikoff, 1962）；**给定样本序列$\left(x^{(1)},y^{(1)}\right),\left(x^{(2)},y^{(2)}\right),\cdots ,\left(x^{(m)},y^{(m)}\right)$，假设对于所有样本$i$，有$\Vert x^{(i)}\Vert \le D$，进一步假设存在单位向量$u$（$\Vert u{\Vert }^2=1$），对于序列中的所有样本有$y^{(i)}\cdot \left(u^T{x}^{(i)}\right)\ge \gamma$（即当$y^{(i)}=1$时$\left(u^T{x}^{(i)}\right)\ge \gamma$，当$y^{(i)}=-1$时$\left(u^T{x}^{(i)}\right)\le \gamma$，也就是$u$将数据分隔开，间隔至少为$\gamma$）。那么，感知算法的误差总数将不会超过${\left(\frac{D}{\gamma }\right)}^2$。

**证明：**感知算法只有在预测错误时调整参数，令${\theta }^{(k)}$为算法在第$k$次预测错误时所使用的参数，则${\theta }^{(1)}=\vec{0}$（因为参数以$\vec{0}$初始化），而如果第$k$次预测错误发生在样本上$\left(x^{(i)},y^{(i)}\right)$，则$g\left({\left(x^{(i)}\right)}^T{\theta }^{(k)}\right)\ne y^{(i)}$，于是有：

$${\left(x^{(i)}\right)}^T{\theta }^{(k)}{y}^{(i)}\le 0\text{\hspace{1em}(2)}$$

从感知更新规则可以得到${\theta }^{(k+1)}={\theta }^{(k)}+y^{(i)}{x}^{(i)}$，于是有：

$$\begin{array}{rl}{\left({\theta }^{(k+1)}\right)}^{T}u& ={\left({\theta }^{(k)}\right)}^{T}u+y^{(i)}{\left(x^{(i)}\right)}^{T}u\\ & \ge {\left({\theta }^{(k)}\right)}^T+\gamma \end{array}$$

通过数学归纳法可知：

$${\left({\theta }^{(k+1)}\right)}^{T}u\ge k\gamma \text{\hspace{1em}(3)}$$

同时，也有：

$$\begin{array}{rl}{\Vert {\theta }^{(k+1)}\Vert }^2& ={\Vert {\theta }^{(k)}+y^{(i)}{x}^{(i)}\Vert }^2\\ & ={\Vert {\theta }^{(k)}\Vert }^2+{\Vert x^{(i)}\Vert }^2+2y^{(i)}{\left(x^{(i)}\right)}^T{\theta }^{(i)}\\ & \le {\Vert {\theta }^{(k)}\Vert }^2+{\Vert x^{(i)}\Vert }^2\\ & \le {\Vert {\theta }^{(k)}\Vert }^2+D^2\end{array}\text{\hspace{1em}(4)}$$

上面的第三步用到了$(2)$式，对$(4)$式再使用归纳法可得：

$${\Vert {\theta }^{(k+1)}\Vert }^2\le k{D}^2\text{\hspace{1em}(5)}$$

结合$(3)$式和$(4)$式：

$$\begin{array}{rl}\sqrt{k}D& \ge \Vert {\theta }^{(k+1)}\Vert \\ & \ge {\left({\theta }^{(k+1)}\right)}^{T}u\\ & \ge k\gamma \end{array}$$

推导第二个不等式使用了单位向量的性质：$z^{T}u=\Vert z\Vert \cdot \Vert u\Vert \cos \varphi \le \Vert z\Vert \cdot \Vert u\Vert$，其中$\varphi$是向量$z$与向量$u$的夹角。结果表明$k\le {\left(\frac{D}{\gamma }\right)}^2$。因此，如果感知算法第$k$次预测错误，则$k\le {\left(\frac{D}{\gamma }\right)}^2$。

（所以，在使用感知算法时，即使输入特征$x^{(i)}\in {\mathbb{R}}^{\infty }$，或向量维数非常高，只要在这个高维空间中，正负样本能被某个间隔分开，该算法会收敛到一个能够完美分隔样本的边界上。）

5. 机器学习应用的一些建议

本节主要有以下几点需要注意：

• 介绍如何将机器学习算法应用在不同的应用问题上的一些建议；
• 本节的材料并不涉及很多数学运算，但仍旧是本课程最难理解的一部分内容；
• 本节的内容在今天可能仍有争议；
• 本节的一些方法并不有利于新的学习算法的研发，只是有利于现有算法的应用；
• 本节的三个重点：
  1. 学习算法的调试诊断；
  2. 误差分析及销蚀分析；
  3. 如何开始用机器学习解决问题
     • 过早统计优化（premature statistical optimization，与软件工程中的过早优化类似，指对机器学习系统中一个非常不重要的部分进行过度的优化）

5.1 调试学习算法

举个例子，比如在写垃圾邮件分类器时，我们小心的选择了$100$个单词作为特征值。（而不是使用全部$50000+$的英语单词）。然后使用贝叶斯逻辑回归算法$\underset{\theta }{\max }\sum _{i=1}^m\log p\left(y^{(i)}\mid x^{(i)},\theta \right)-\lambda \Vert \theta {\Vert }^2$，再使用梯度下降法算出结果。测试模型发现，得到了不可接受的20%的错误率。

接下来怎么办？

通常的想法是想方设法的优化这个算法，包括：

• 获得更多的训练样本；
• 寻找更小的特征值集合；
• 寻找更大的特征值集合；
• 尝试改变特征值，比如“从邮件头部获取信息”V.S.“从邮件正文获取信息”；
• 让算法再多迭代几次（怀疑算法没有完全收敛）；
• 尝试换用牛顿法计算参数；
• 给$\lambda$赋不同的值；
• 尝试换用SVM算法。

这里仅列出了八项，而在实际的学习系统中，能够列出上百项可行的改进方法，其中的某些尝试可能会有效（比如获取更多的训练样本），但显然非常浪费时间，而且非常需要运气，就算解决了也可能仍旧不知道问题出在哪。

所以，我们应该先诊断问题所在，然后再想方法解决。那么，对于上面的例子：

假设我们怀疑问题出现在：

• 过拟合（高方差）；
• 特征值过少，无法有效分类（高偏差）

诊断：

• 高方差的特点：训练误差比测试误差小很多；
• 高偏差的特点：训练误差也很高；

高方差的典型学习曲线：

• 当训练集$m$增大时测试误差也会继续降低（而训练误差会持续增加，因为样本越多，越难以完美拟合），建议增加训练样本；
• 训练误差与测试误差中的差距过大。

高偏差的典型学习曲线：

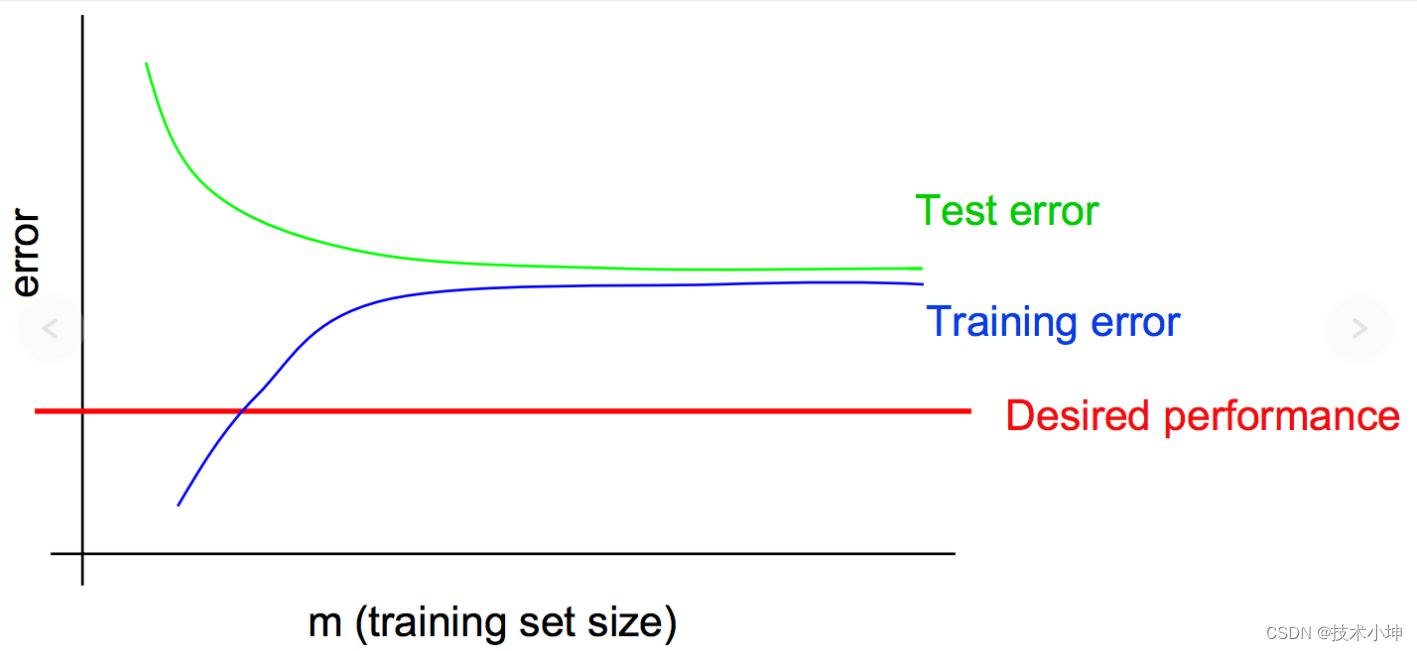
• 即使是训练误差也是高的不可思议（还可以发现增加训练样本的效果已经很不明显了，而此时增加训练样本只会使训练效果越来越差，因为通常的训练误差是关于训练样本的单调增函数）；
• 而训练误差与测试误差间的差距很小。

（所以，可以通过判断训练误差与测试误差间的距离判断）

于是，对于这个使用梯度下降法实现的贝叶斯逻辑回归，回到前面列出的八项解决方案：

• 获得更多的训练样本；（有助于修复高方差）
• 寻找更小的特征值集合；（有助于修复高方差）
• 寻找更大的特征值集合；（有助于修复高偏差）
• 尝试改变特征值，比如“从邮件头部获取信息”V.S.“从邮件正文获取信息”；（有助于修复高偏差）
• 让算法再多迭代几次（怀疑算法没有完全收敛）；
• 尝试换用牛顿法计算参数；
• 给$\lambda$赋不同的值；
• 尝试换用SVM算法。

上面这个关于方差与偏差的诊断是一个常见的机器学习调试方法。而对于别的问题则需要我们构造自己的诊断方法，找出问题。

我们再举一个例子：

• 使用贝叶斯逻辑回归时，对垃圾邮件存在$2$的误判，对非垃圾邮件也存在$2$的误判（也就是对正常邮件的误判率过高）；
• 而使用带有线性核的SVM时，对垃圾邮件存在$10$的误判，对非垃圾邮件存在$0.01$的误判（在正常范围内）；
• 因为运算效率的问题，我们更希望使用逻辑回归。

这次，又该怎么办？

通常，伴随这种问题会产生更常见的问题：

• 收敛性问题：我们的算法（对于逻辑回归的梯度下降法）收敛了吗？

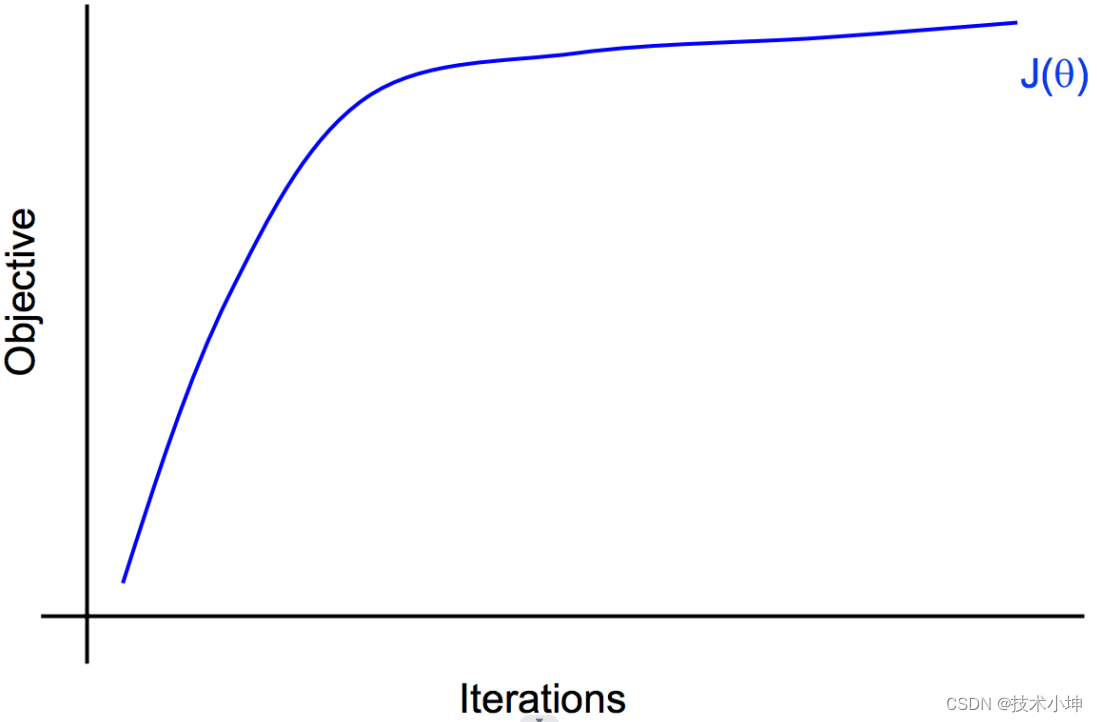
通过直接观察目标函数值经常难以判断算法是否已经收敛。所以，除了直接观察目标函数关于迭代次数的曲线以外，我们可能需要更好的判断收敛的方法。

• 是否找到了正确的优化函数，比如在垃圾邮件分类器的例子中，我们真正关心的是这个加权准确率函数：

$$a(\theta )=\sum _i{w}^{(i)}1\left\{h_{\theta }(x^{(i)})=y^{(i)}\right\}$$

非垃圾邮件的权值$w^{(i)}$更高，因为我们更关心对垃圾邮件的预测，更希望模型能够准确挑出垃圾邮件。）

• 那么，是使用贝叶斯逻辑回归？惩罚项系数$\lambda$设置正确吗？

$$\underset{\theta }{\max }J(\theta )=\sum _{i=1}^m\log p\left(y^{(i)}\mid x^{(i)},\theta \right)-\lambda \Vert \theta {\Vert }^2$$

• 还是使用SVM？惩罚项系数$C$设置正确吗？

$$\begin{array}{rl}\underset{w,b}{\min }& \Vert w^2\Vert +C\sum _{i=1}^m{\xi }_i\\ s.t.& y^{(i)}\left(w^T{x}^{(i)}-b\right)\ge 1-{\xi }_i\end{array}$$

我们从这个例子引出第二种诊断方法，判断究竟是算法没有收敛，还是在于一开始目标函数的选择上。假设尽管SVM比贝叶斯逻辑回归表现更好，但是我们还是希望使用贝叶斯逻辑回归：

令${\theta }_{\mathrm{SVM}}$为由SVM求出的参数；令${\theta }_{\mathrm{BLR}}$为贝叶斯逻辑回归生成的参数。继续列出我们关心的加权准确率：

$$a(\theta )=\sum _i{w}^{(i)}1\left\{h_{\theta }(x^{(i)})=y^{(i)}\right\}$$

因为SVM的表现更好，所以其加权准确率更高$a\left({\theta }_{\mathrm{SVM}}\right)>a\left({\theta }_{\mathrm{BLR}}\right)$。因为贝叶斯逻辑回归的目标函数为$\underset{\theta }{\max }J(\theta )=\sum _{i=1}^m\log p\left(y^{(i)}\mid x^{(i)},\theta \right)-\lambda \Vert \theta {\Vert }^2$，所以我们诊断两个算法目标函数的结果：

$$J\left({\theta }_{\mathrm{SVM}}\right)\stackrel{?}{>}J\left({\theta }_{\mathrm{BLR}}\right)$$

• 第一种情况：$a\left({\theta }_{\mathrm{SVM}}\right)>a\left({\theta }_{\mathrm{BLR}}\right)$，且$J\left({\theta }_{\mathrm{SVM}}\right)>J\left({\theta }_{\mathrm{BLR}}\right)$。

  因为BLR的目标是最大化$J(\theta )$，则可以看出BLR并没有完成这个目标，即${\theta }_{\mathrm{BLR}}$并没有使$J$取到最大值，算法的收敛出了问题。也就是说，这是优化算法的问题。

• 第二种情况：$a\left({\theta }_{\mathrm{SVM}}\right)>a\left({\theta }_{\mathrm{BLR}}\right)$，且$J\left({\theta }_{\mathrm{SVM}}\right)\le J\left({\theta }_{\mathrm{BLR}}\right)$。

  这意味着BLR成功的最大化了$J(\theta )$，但是SVM虽然在最大化目标函数这方面做得没有BLR好，但是SVM的加权准确率$a(\theta )$竟依旧比BLR高。说明如果我们关心$a(\theta )$，那么$J(\theta )$就不是一个恰当的目标函数。也就是说，这是目标函数选择的问题。

再回到我们列出的八项解决方案：

• 获得更多的训练样本；（有助于修复高方差）
• 寻找更小的特征值集合；（有助于修复高方差）
• 寻找更大的特征值集合；（有助于修复高偏差）
• 尝试改变特征值，比如“从邮件头部获取信息”V.S.“从邮件正文获取信息”；（有助于修复高偏差）
• 让算法再多迭代几次（怀疑算法没有完全收敛）；(有助于修复算法收敛问题)
• 尝试换用牛顿法计算参数；(有助于修复算法收敛问题)
• 给$\lambda$赋不同的值；(有助于修复目标函数选择问题)
• 尝试换用SVM算法。(有助于修复目标函数选择问题)

再来简要的介绍一个**强化学习（RL: reinforcement learning）**的例子——用学习算法控制一个直升机，分为以下三步：

1. 搭建一个遥控直升机模拟器，类似一个带操纵杆的模拟器，可以模拟飞行；
2. 选择一个成本函数，也称作奖励函数（reward function），比如$J(\theta )=\Vert x-x_{\mathrm{desired}}\Vert$（其中的$x$代表直升机的位置，这里示例的函数表示直升机实际位置与期望位置的平方误差）；
3. 在模拟器中运行强化学习算法控制直升机并尝试最小化成本函数，${\theta }_{\mathrm{RL}}=\arg \underset{\theta }{\min }J(\theta )$。

现在，假设我们做了以上三步，发现得到的控制参数${\theta }_{\mathrm{RL}}$的表现比人类直接操作差很多，接下来该怎么办？我们能直接想到的——是升级模拟器（也行是模拟器不够精确，没有考虑到更精确的空气动力学因素，需要收集到飞机附近更精确的气流扰动）？还是修改成本函数$J$（也许平方误差并不合适，也许人类操纵者考虑的不是误差平方，而是更加复杂的运算）？或是修改RL算法（也许RL算法不够好，也许它收敛的不够迅速）？

对于表现不好的参数${\theta }_{\mathrm{RL}}$，我们先做出以下假设：

1. 假设模拟器已经够精确了（也就是我们对直升机的建模是准确的）；
2. 假设强化学习算法能够在模拟器中正确的控制直升机，从而求得最小化的$J(\theta )$；
3. 假设最小化$J(\theta )$确实可以正确的控制直升机（即强相关的）。

如果这些假设都成立，那么我们的算法理论上就能够很好的控制直升机了。但现实是${\theta }_{RL}$并不能很好的控制直升机，所以上面的假设至少有一个是不成立的。我们希望找出问题，于是用到的诊断方法如下：

1. 检查模拟器，如果算法在模拟器中可以正常工作，但是在现实中不行，那么问题可能出在模拟器上。于是，我们应该改进模拟器；
2. 令${\theta }_{\mathrm{human}}$为人工操作时的参数（让人在模拟器中操作飞机，并记录成本函数的值，在这里就是平方误差的均值），如果$J({\theta }_{\mathrm{human}})<J({\theta }_{\mathrm{RL}})$，则是增强学习算法出了问题。（算法并没有找到使成本函数$J$最小的参数取值。）
3. 如果$J({\theta }_{\mathrm{human}})\ge J({\theta }_{\mathrm{RL}})$，则应是成本函数出了问题。（最小化错误的函数并不能增强算法控制飞机的效果。）

不过，通常遇到问题时，我们需要自己寻找诊断方法查找问题。

有时，即使一个算法能够正常工作，我们也可以运行诊断方法来看算法是如何运作的，比如用于：

• 让我们理解程序的问题：比如手头有一个跑了几个月甚至几年的重要学习算法，那么直观的知道算法是如何运行的，知道算法在什么时候有效，在什么时候失效，对我们个人的提高都非常有帮助；
• 写论文时：诊断及误差分析都能帮助我们深入理解问题，并为论点提供有力证据。比起“如此，算法的表现很好”而言，说“算法因为组件X才有了如此优异的表现，这里是我的论据”则来的更有意思。

于是，也引出了误差分析——一个很好的机器学习实践，可以帮助我们更好的理解误差产生的根源。

5.2 误差分析

许多实际的人工智能、机器学习应用会通过“流水线”的方式将不同的学习组件组装起来，比如从图片中识别人脸的应用：

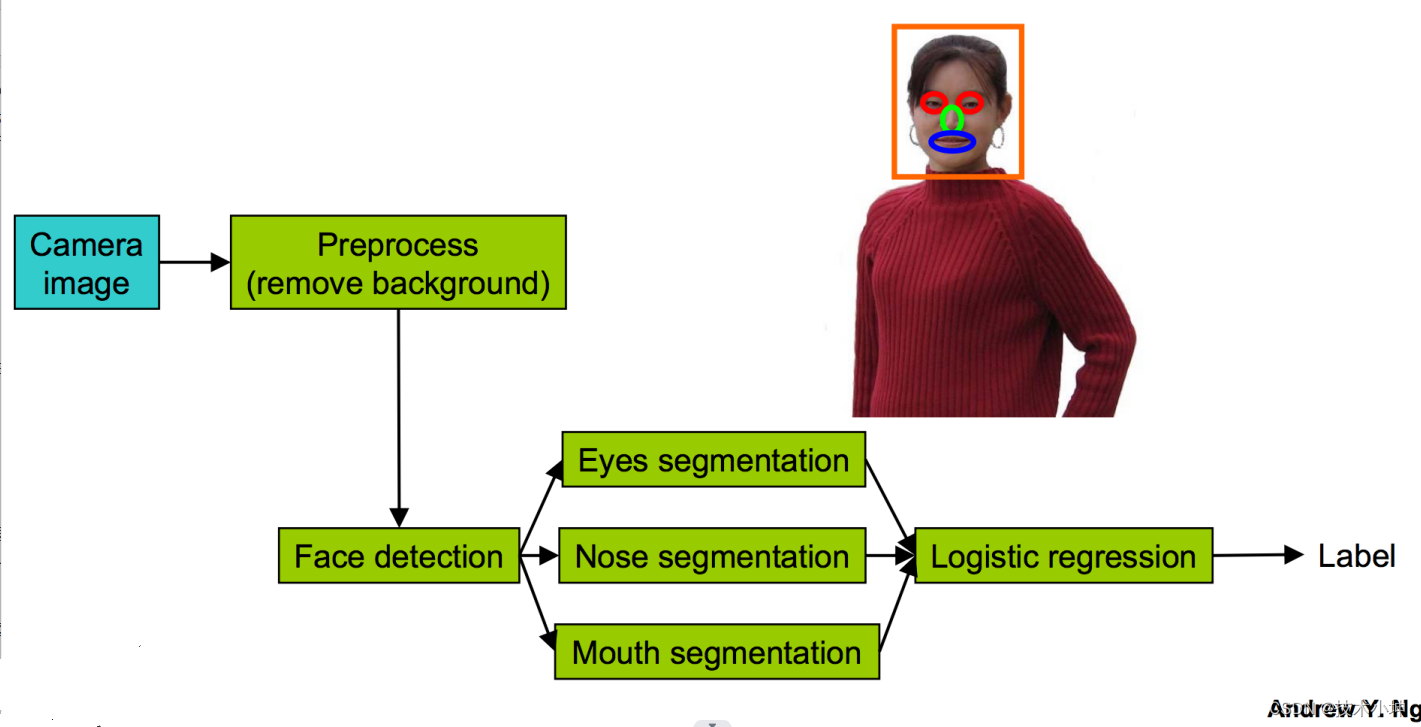
那么我们应该分析：

1. 误差由哪些组件造成，每个组件造成的误差是多少？
2. 对每一个组件使用基准真值测试，看每一个组件对整个系统准确率的影响。整个流程大概是这样的：

• 启初，我们发现面部识别系统判断的准确率是$85$；
• 第一步，我们手动去除图片的背景，也就是直接给系统提供已经去除背景的图片，之后发现系统的准确率提高到$91$；
• 第二步，我们手动的告诉系统每一张图片中面部的坐标，之后发现系统准确率提升到$95$；
• 以此类推，我们不停的手动告知系统，用基准真值代替每一个组件通过计算得出的值，我们会接着告诉系统眼睛、鼻子、嘴巴的具体位置……系统最终会得到$100$的准确率。

然后，就会得到一张表，记录着每个组件对系统准确率的影响：

$$\begin{array}{cc}\text{Component}& \text{Accuracy}\\ \text{Overall system}& 85\%\\ \text{Preprocess(remove background)}& 85.1\%\\ \text{Face detection}& 91\%\\ \text{Eyes segmentation}& 95\%\\ \text{Nose segmentation}& 96\%\\ \text{Mouth segmentation}& 97\%\\ \text{Logistic regression}& 100\%\end{array}$$

从这里我们就可以看出，如果我们改进预处理步骤（移除背景），对整个系统准确率的影响仅有$0.1$；而如果我们改进面部检测算法，则整个系统将会提高$6$的准确率。

5.3 销蚀分析

通过前面的介绍，我们知道**误差分析（error analysis）**是尝试解释系统当前表现与我们期待的完美表现之间的差距；

而**销蚀分析（ablative analysis）**是尝试解释系统基准表现（可能比当前差很多）与当前表现之间的差距。

还是用前面的例子，由于我们机智的向逻辑回归中加入了很多有趣的特征值，于是得到了一个非常好用的垃圾邮件分类器，其中的特征值包括：

• 拼写检查；
• 发件人主机信息；
• 邮件头信息；
• 邮件正文分析特征；
• 邮件携带的JavaScript分析特征；
• 邮件中内嵌的标签分析特征；
• 等等……

我们现在想知道，上面那些特征是真正起作用的？

假设使用简单的逻辑回归，不加入上面任何特征时，系统具有$94$的准确率。那么，这些特征是如何将系统准确率从$94$提高到$99.9$的？

销蚀分析的步骤，就是从系统中每次去掉一个组件，记录并观察系统是如何被瓦解的（留意准确率因何降低，特别是突降）。

$$\begin{array}{cc}\text{Component}& \text{Accuracy}\\ \text{Overall system}& 99.9\%\\ \text{Spelling correction}& 99\%\\ \text{Sender host features}& 98.9\%\\ \text{Email header features}& 98.9\%\\ \text{Email text parser features}& 95\%\\ \text{Javascript parser}& 94.5\%\\ \text{Features from images}& 94\%\end{array}$$

从列表中可以清楚的看到，邮件正文分析特征对整个系统的提升最为显著。不过，调整销蚀顺序可能也会影响准确率，我们介绍的误差分析、销蚀分析并不是一成不变的。比如有些方法会从中剔除一个组件观察记录后放回，再剔除另一个组件，周而复始，调试方法有很多，关键是在相应的时候灵活使用、发明自己的调试方法。

5.4 着手处理学习问题的一些通用建议

着手解决一个学习问题通常有两种实现方式：

1. 精心设计

• 花费很长的时间精确的设计特征值、收集有效的训练样本，并设计正确的算法架构；
• 用代码实现设计，并希望它能够正常工作。

这种实现方式的优点是：我们会得到更好的，扩展性更强的算法。这种方式通常会得到新的、优雅的学习算法，将会为机器学习的基础研究做出贡献。
2. 边编写边修改

• 先快速实现一个简陋的原型；
• 运行误差分析并诊断这个实现的问题所在，然后修复问题并重复这个步骤，直到得到一个满意的解决方案。

这种实现方式的优点是：我们通常会更快的解决问题，对快速占领市场很有帮助。

就拿上面的面部识别的系统来说，对于设计如此复杂的一个系统，我们在一开始很难知道哪些组件容易实现、哪些组件需要花时间研究等等，只有通过实现一个快速原型，多试几次才能确定那些对系统影响显著的组件并给予深入研究。不过，这个建议并不适合研发新的学习算法，对于新的算法，就需要从一开始深入研究并精心设计系统的每一个步骤，而不是快速实现原型后不停的修补模型。

需要注意的是，同软件工程中的过早优化类似，我们要避免在系统设计阶段发生过早统计优化，比如上面面部识别例子中，如果我们在设计时过早的花费很多精力优化预处理模块，则在后面就会发现，这一步对整个系统影响甚微。

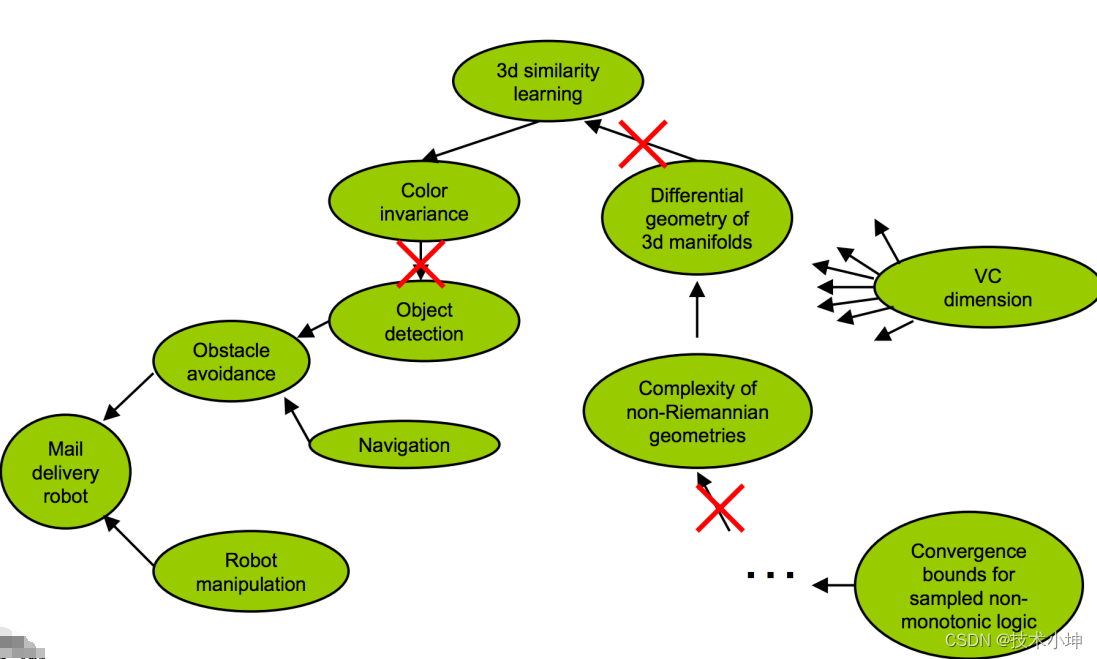
另外，我们不应该在理论上做过度的联想，比如我们想要实现一个自动投递邮件的机器人，那么会需要障碍躲避的知识和机器人操控的知识，如果要实现障碍躲避就需要实现障碍侦测和导航，如果要实现障碍侦测则需要避免不同时间光线对物体的光照色彩的影响，所以需要一套独立于色彩的物体识别系统，而为了实现这个系统，我们需要研究三维物体表面的微分几何，因为这可以帮助我们确定两个不同颜色的物体可能是同一个物体，为了理解上面的这些理论，我们需要学习非黎曼几何的复杂性……等等等等等等……

不过问题是，这些知识并不是真正强相关的，其中的某些箭头可能只是谋篇论文道听途说的，我们应该专注于解决眼前的工程问题，并且只相信我们能够亲自确定的存在关联的知识点，只有亲自确定后才选择是否深入研究某个特定领域的知识。

5.5 总结

• 通常，我们花费在调试及诊断学习算法上的时间都是值得的；
• 通常，我们需要发挥自己的聪明才智，去设计调试特定问题的方法；（对于一个机器学习问题，我们有时会花费三分之一、甚至一半的时间在调试及诊断上。）
• 误差分析及销蚀分析可以让我们深入的理解问题，看到究竟是那些因素影响算法的表现；
• 介绍了两种实现方式：
  • 精心设计后实现（可能伴有过早统计优化的风险）；
  • 快速实现原型后不断进行诊断、调试、修改；