CF number theory 1700 ~ 1900
30道还算有趣但是很简单的题目(摘自 div1, div2 等).
1. Problem - 1548B - Codeforces (再写)
在一个序列上找到最长的连续子区间,使得存在 m ≥ 2 m \ge 2 m≥2,子区间内所有数字模 m m m 同余.
如果每个数字模 m m m 的值都一样,设模数为 d d d,那么说明 a i − d a_i - d ai−d 模 m m m 都为 0 0 0,说明 gcd ( a − d , b − d ) = gcd ( a − d , ∣ a − b ∣ ) > 1 \gcd(a-d, b-d) =\gcd(a-d, |a - b|) > 1 gcd(a−d,b−d)=gcd(a−d,∣a−b∣)>1. 就是在差分数组上找到最长的一段子区间他们的最大公约数不为 1 1 1. 然后答案就是这个区间的长度加1. 考虑到最大公约数的单调性用双指针即可.
2. Problem - 1547F - Codeforces
给一个序列环 a a a ( a n − 1 a_{n-1} an−1 与 a 0 a_0 a0 相接),每次可以用一个新的序列 b b b 替代,即 b i = gcd ( a i , a i + 1 m o d n ) b_i = \gcd(a_i, a_{i + 1\ \bmod\ n}) bi=gcd(ai,ai+1 mod n),问最少需要替换多少次才能使这个序列的所有数字都是一样的.
观察可以发现,设原始序列所有数字的最大公约数为 d d d,那么所有数字最终都会变成 d d d,并且 a i a_i ai 变化为 d d d 的次数是从 a i a_i ai 开始能够延伸到最短的距离,且当前的子区间的最大公约数为 d d d. 至于环怎么处理,把这个序列复制一遍接在后面变成之前的两倍长度即可.
3. Problem - 1538D - Codeforces
暴力分解质因数即可.
4. Problem - 1537D - Codeforces (再写)
给一个正整数 n ( n ≤ 1 0 9 ) n(n \le 10 ^ 9) n(n≤109),两个人轮流玩游戏,每次进行的操作是选 n n n 的一个因数 d d d,要求 d ≠ 1 d \ne 1 d=1 且 d ≠ n d \ne n d=n. 不能操作的人输掉。问最后谁会赢.
打个表,规律显然。当 n n n 是奇数,或者 n n n 是2的奇数次幂的时候,先手必输。其他情况先手必赢。可以这样子分析:
总共有三种情况:
- n n n 是奇数
- n n n 是偶数并且不是 2 2 2 的幂
- n n n 是 2 2 2 的幂
第一种情况:如果 n n n 是质数就输了。否则只能减去一个奇数,变为第二种情况.
第二种情况:可以减去一个奇数变成第一种情况,然后对手在操作一步变成第二种情况. 直到丢给对手一个奇质数为止。因此这种情况必赢,而第一种情况必输.
第三种情况,只有将 n n n 减半,才能避免对手进入第二种情况。因此只有当前的幂次是偶数的时候才能赢.
5. Problem - 1485C - Codeforces
问 1 ≤ a ≤ x , 1 ≤ b ≤ y 1 \le a \le x,1 \le b \le y 1≤a≤x,1≤b≤y,有多少 ( a , b ) (a, b) (a,b) 满足 ⌊ a b ⌋ = a m o d b \lfloor \dfrac{a}{b} \rfloor = a \bmod b ⌊ba⌋=amodb.
相当于
q
b
+
q
≤
x
qb + q \le x
qb+q≤x,即
q
≤
x
b
+
1
q \le \dfrac{x}{b + 1}
q≤b+1x.
满足条件的
q
q
q 在
1
≤
q
≤
min
(
b
−
1
,
x
b
+
1
)
1 \le q \le \min\Big(b-1, \dfrac{x}{b + 1}\Big)
1≤q≤min(b−1,b+1x)
因此在前
x
\sqrt x
x 暴力枚举,具体来说就是
b
−
1
≤
x
b
+
1
b - 1 \le \dfrac{x}{b + 1}
b−1≤b+1x 的时候,后面整除分块.
6. Problem - 1477A - Codeforces
给 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 个数字集合,可以从中任意挑选两个数字 x , y x, y x,y,将新生成的数字 2 x − y 2x - y 2x−y 加到这个集合中. 问最后集合中是否可以出现数字 k k k.
假设挑选的两个数字是 a a a 和 a + d a + d a+d, 那么可以生成的数字便是 a + k d , k ∈ Z a + kd,k \in \Z a+kd,k∈Z. 对数组排序,计算相邻数字的差,对这些差求一个 gcd \gcd gcd,最后扫一遍看看是否存在 gcd ∣ ∣ k − x i ∣ \gcd \mid |k - x_i| gcd∣∣k−xi∣.
7. Problem - 1470B - Codeforces
给出 n n n 个数,若 l c m ( x , y ) g c d ( x , y ) \dfrac{lcm(x,y)}{gcd(x,y)} gcd(x,y)lcm(x,y) 为完全平方数称 x , y x,y x,y 是相邻的. 每一秒都会发生以下的情况: 每个数被所有和自己相邻数字(包括自己)的乘积所替换. 设 d i d_i di 为和数字 a i a_i ai 相邻数字的数量. 给出 q q q 组询问,问第 i i i 秒最大的 d i d_i di
把每个数质因数分解,如果当前质因子 p i c i p_i^{c_i} pici 的幂次为奇数,就用 p i p_i pi 代替,如果是幂次是偶数,就用 1 1 1 来代替,得到一个新的数字加到集合中。这样子分析,发现最多合并两次,数组就不会变了.
8. Problem - 1469D - Codeforces
给序列 1 , 2 , 3 , . . . , n 1, 2, 3, ...,n 1,2,3,...,n,其中 n ≤ 1 0 5 n \le 10^5 n≤105. 可以任意挑选两个下标 x , y x, y x,y,令 a x = ⌈ a x a y ⌉ a_x = \lceil \dfrac{a_x}{a_y}\rceil ax=⌈ayax⌉. 最后让这个序列变成 n − 1 n - 1 n−1 个 1 1 1 和 1 1 1 个 2 2 2. 最多执行 n + 5 n + 5 n+5 次操作
构造题。我们发现对 1 0 5 10^5 105 一直开方,大概就开几次就到了1. 因此可以找到一个基准点 x x x,把大于 x x x 的数字除以 n n n,小于等于 x x x 的数继续搜索啥的. 基准点我挑选的是 n \sqrt n n 附近的数字,具体来说就是 ( ⌊ n ⌋ + ⌈ n ⌊ n ⌋ ⌉ ) / 2 (\lfloor\sqrt n \rfloor + \lceil \dfrac{n}{\lfloor\sqrt n \rfloor} \rceil) / 2 (⌊n⌋+⌈⌊n⌋n⌉)/2. 为什么是这个呢?多试几个 n \sqrt n n 附近的数字之后试出来的.
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef pair<int, int> P;
vector<P> ans;
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
int n;
scanf("%d", &n);
int now = n;
ans.clear();
while(now != 2)
{
int x = sqrt(now);
if(x * x != now) x++;
for(int i = x + 1; i < now; i++) ans.push_back({i, n});
ans.push_back({n, x});
if(x * x == now) ans.push_back({x, n});
now = (now + x - 1) / x;
}
printf("%d\n", (int)ans.size());
for(const auto& p : ans)
{
printf("%d %d\n", p.x, p.y);
}
}
return 0;
}
9. Problem - 1468F - Codeforces
给你 n n n 个人的位置和他们眼睛看的方向 这 n n n 个人同时开始顺时针旋转 360°. 问 :在旋转过程中 有多少对人进行了眼神接触
统计所有向量,能够眼神接触的只有方向相反的向量.
10. Problem - 1401D - Codeforces
给出一棵树和一个大数 k k k ,请你给这棵树上的每条边分配一个边权,使得这棵树上的节点两两之间的路径总和最大,同时边权中 1 1 1 的数量尽可能少,同时所有边权的乘积等于 k k k。输入的时候直接给出了 k k k 的所有质因子.
考虑每个边的贡献,计算每个边可以包含在多少路径之中。深搜一遍,该边在
s
z
[
v
]
∗
(
n
−
s
z
[
v
]
)
sz[v] * (n - sz[v])
sz[v]∗(n−sz[v]) 条路径之中。然后对边排个序,质数排个序,从大到小看就行了.
一定要讨论
m
>
n
−
1
m > n - 1
m>n−1 的情况,不卡时间的话全开long long. 小心溢出.
11. Problem - E2 - Codeforces
其实这个题我直接放 Hard Version 到这里了
小女孩手上有
x
x
x 颗糖,
n
n
n 个对手,第
i
i
i 个对手手里有
a
i
a_i
ai 个糖. 小女孩可以按照
n
n
n 的排列数,选择需要比较对手的次序。
f
(
x
)
f(x)
f(x) 代表小女孩最开始有
x
x
x 个糖时合法排列数的数量,合法排列是按照此顺序比赛小女孩可以赢。赢的标准是,每次比较时,小女孩手上糖果的数量,大于等于当前对手的糖果数量,若赢,小女孩手上还能增加
1
1
1 颗糖。若
f
(
x
)
m
o
d
p
≠
0
f(x) \bmod p \ne 0
f(x)modp=0 (p是输入数据给出的质数),那么记录此时的
x
x
x,寻找所有可能的
x
x
x ,输出满足条件的
x
x
x 数量,并按升序,输出相应的
x
x
x 值。
思路是这样的,考虑到
f
(
x
)
f(x)
f(x) 应该是若干阶乘之积. 如果让
f
(
x
)
m
o
d
p
≠
0
f(x) \bmod p \ne 0
f(x)modp=0,那么就不能出现
p
!
p!
p!.
x
x
x 的最小值容易判断,最大值怎么求呢?先排序,其实就是当第
p
p
p 个位置的数字放到第
1
1
1 个位置的时候,小女孩就不能赢。因此
x
≤
a
p
−
1
x \le a_p - 1
x≤ap−1. 同理,第
a
p
+
1
a_{p + 1}
ap+1 不能放到第
2
2
2 个位置。以此类推.
因此,
x
x
x 应满足
∀
i
∈
[
1
,
n
]
,
x
≥
a
i
−
(
i
−
1
)
\forall i \in [1, n], x \ge a_i - (i - 1)
∀i∈[1,n],x≥ai−(i−1),以及
∀
i
∈
[
p
,
n
]
,
x
≤
a
i
−
(
a
i
−
p
)
−
1
\forall i \in [p, n], x \le a_i - (a_i - p) - 1
∀i∈[p,n],x≤ai−(ai−p)−1. 这样的
x
x
x 都是合法的.
12. Problem - 1325D - Codeforces
给两个数字 u , v u,v u,v,找到一个长度最短的序列,使得序列的异或和为 u u u,序列的和等于 v v v.
可以分析一下. 特殊情况如下:如果
u
>
v
u > v
u>v 无解,
u
=
v
=
0
u = v = 0
u=v=0,直接输出
0
0
0(题目要求). 如果
u
=
v
u = v
u=v,那么序列长度为1,就是
u
u
u.
对于一般情况
u
<
v
u < v
u<v 呢?如果
v
−
u
v - u
v−u 是一个奇数,那么一定无解。因为如果序列里面奇数的个数是奇数,那么
u
u
u 和
v
v
v 都是奇数。否则都是偶数。
下面讨论
v
−
u
v - u
v−u 是偶数的情况。首先序列
[
u
,
v
−
u
2
,
v
−
u
2
]
[u, \dfrac{v-u}{2}, \dfrac{v - u}{2}]
[u,2v−u,2v−u] 一定满足. 因此长度至多为3. 那什么时候长度可以是
2
2
2 呢?我们想办法把
v
−
u
2
\dfrac{v - u}{2}
2v−u 分为两部分,一部分加到
u
u
u 里面,并且保证两个数的异或仍然是
u
u
u . 对于
u
u
u 的某个数位为0的位置,塞1个1,另外那个数字对应位置也为1,要么直接塞个0. 当然也有其他方法,但是都可以转化为这种方法。因此当
u
&
v
−
u
2
=
0
u\ \&\ \dfrac{v - u}{2} = 0
u & 2v−u=0,就可以这么弄,即两个数分别为
u
+
v
−
u
2
,
v
−
u
2
u + \dfrac{v - u}{2},\dfrac{v - u}{2}
u+2v−u,2v−u.
13. Problem - 1295D - Codeforces
给定 a , m ( 1 ≤ a , m ≤ 1 0 10 ) a, m(1 \le a, m \le 10^{10}) a,m(1≤a,m≤1010),问有多少个 x ( 0 ≤ x ≤ m − 1 ) x(0 \le x\le m-1) x(0≤x≤m−1),使得 gcd ( a , m ) = gcd ( a + x , m ) \gcd(a, m) = \gcd(a + x, m) gcd(a,m)=gcd(a+x,m).
很妙的题,由于 gcd ( x , m ) = gcd ( x m o d m , m ) \gcd(x, m) = \gcd(x \bmod m, m) gcd(x,m)=gcd(xmodm,m),等价于求 x ∈ [ 0 , m − 1 ] , gcd ( x , m ) = gcd ( a , m ) x \in [0, m - 1], \gcd (x, m) = \gcd(a, m) x∈[0,m−1],gcd(x,m)=gcd(a,m)。 令 d = gcd ( a , m ) d = \gcd(a, m) d=gcd(a,m),就是求 x ∈ [ 0 , m − 1 d ] , gcd ( x d , m d ) = 1 x \in [0, \dfrac{m - 1}{d}],\gcd(\dfrac{x}{d} ,\dfrac{m}{d}) = 1 x∈[0,dm−1],gcd(dx,dm)=1. 即求 φ ( m d ) \varphi(\dfrac{m}{d}) φ(dm).
14. Problem - 1260C - Codeforces
有一个从 0 0 0 开始标号的无限长的木板,给 r , b r, b r,b,需要把下标是 r r r 倍数的格子涂成红色,下标是 b b b 的倍数的地方涂成蓝色,下标既是 r r r 的倍数又是 b b b 的倍数的地方涂成红色或者蓝色都可以。问是否避免连续 k k k 个涂颜色的地方涂了相同的颜色?
不妨设
r
<
b
r < b
r<b,其实就是找到两个
b
b
b 之间是否有
k
k
k 个
r
r
r. 先
r
′
=
r
(
r
,
b
)
,
b
′
=
b
(
r
,
b
)
r' = \dfrac{r}{(r, b)}, b' = \dfrac{b}{(r, b)}
r′=(r,b)r,b′=(r,b)b. 其实就是找到
m
∈
[
1
,
b
′
−
1
]
,
m
r
′
m
o
d
b
m \in [1, b' - 1], mr' \bmod b
m∈[1,b′−1],mr′modb 的最小值,设为
d
d
d,那么最多有连续
⌈
b
′
−
1
r
′
⌉
\lceil \dfrac{b'-1}{r'} \rceil
⌈r′b′−1⌉ 个红色.
还可以用反证法证明
m
∈
[
1
,
b
′
−
1
]
,
m
r
′
m
o
d
b
m \in [1, b' - 1], mr' \bmod b
m∈[1,b′−1],mr′modb 就是从
[
1
,
2
,
.
.
.
,
b
′
−
1
]
[1, 2, ..., b'-1]
[1,2,...,b′−1] 的一个重排. 因此
d
d
d 最小值为
1
1
1.
15. Problem - 1254B1 - Codeforces
给一个 01 01 01 序列,可以把某一个数字大于 0 0 0 的位置的数字减 1 1 1,然后相邻的位置的数字加 1 1 1,花费为 1 1 1. 存在 k > 1 k > 1 k>1,使得每个位置的数字都可以被 k k k 整除.
首先, k k k 选择 ∑ a i \sum a_i ∑ai 的质因子即可. 然后一块儿一块儿的凑,每次都往每一块儿的中位数去凑。相当于往 p / 2 p / 2 p/2 的位置移动. 枚举每个质因子计算即可.
16. Problem - 1225D - Codeforces
题意:给一个长度为 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 的序列, a i ≤ 1 0 5 a_i \le 10^5 ai≤105,正整数 k ( 2 ≤ k ≤ 1 0 5 ) k(2 \le k \le 10^5) k(2≤k≤105),问有多少组 ( i , j ) (i, j) (i,j),其中 1 ≤ i < j ≤ n 1 \le i < j \le n 1≤i<j≤n,存在正整数 x x x,有 a i ⋅ a j = x k a_i \cdot a_j = x^k ai⋅aj=xk
设 a i = p 1 c 1 ⋅ p 2 c 2 . . . p m c m a_i = {p_1}^{c_1}\cdot p_2^{c_2}...p_m^{c_m} ai=p1c1⋅p2c2...pmcm,在 map 中存下 p 1 c 1 m o d k ⋅ p 2 c 2 m o d k . . . p m c m m o d k {p_1}^{c_1 \bmod k}\cdot p_2^{c_2 \bmod k}...p_m^{c_m \bmod k} p1c1modk⋅p2c2modk...pmcmmodk. 然后遍历 map,求出 p 1 k − ( c 1 m o d k ) ⋅ p 2 k − ( c 2 m o d k ) . . . p m k − ( c m m o d k ) {p_1}^{k -(c_1 \bmod k)}\cdot p_2^{k - (c_2 \bmod k)}...p_m^{k - (c_m \bmod k)} p1k−(c1modk)⋅p2k−(c2modk)...pmk−(cmmodk),将此数记为 a i ‾ \overline{a_i} ai. 把两者的个数相乘,答案除以2. 不过还有一个需要特判,就是 a i = a i ‾ a_i = \overline{a_i} ai=ai 时是 C c n t 2 C_{cnt}^2 Ccnt2.
17. Problem - 1220D - Codeforces
给一个集合 B B B,用 B B B 生成一个图。生成过程是这样的:如果正整数 i i i 和正整数 j j j 有无向边当且仅当 ∣ i − j ∣ ∈ B |i - j| \in B ∣i−j∣∈B. 现在删掉集合 B B B 中的最少的元素,使得生成的图是二分图.
自行证明几个结论:
- B B B 中同时出现奇数和偶数时一定不成立。
- 如果 B B B 中都是奇数,那么一定成立。
- B B B 中都是偶数时,把 B B B 中的每个数字分解为 p ⋅ 2 q p\cdot 2^q p⋅2q,其中 p p p 不含有因子 2 2 2. 那么所有 q q q 相同的数字组成的集合一定成立(因为所有数字除以 2 q 2^q 2q 之后,倍数关系没有改变,就转化为情况 1 1 1). q q q 不相等的两个数字一定不成立(可以转化为情况 2 2 2)
因此把所有数字分解为 p ⋅ 2 q p \cdot 2^q p⋅2q 的形式,按照 q q q 相等时来划分集合即可,最大的子集即为合法集合.
18. Problem - 1195D2 - Codeforces
定义
if p ≥ q p≥q p≥q then f ( a 1 … a p , b 1 … b + q ) = a 1 a 2 … a p − q + 1 b 1 a p − q + 2 b 2 … a p − 1 b q − 1 a p b q f(a_1…a_p,b_1…b+q)=a_1a_2…a_{p−q+1}b_1a_{p−q+2}b_2…a_{p−1}b_{q−1}a_pb_q f(a1…ap,b1…b+q)=a1a2…ap−q+1b1ap−q+2b2…ap−1bq−1apbq;
if p < q p<q p<q then f ( a 1 … a p , b 1 … b q ) = b 1 b 2 … b q − p a 1 b q − p + 1 a 2 … a p − 1 b q − 1 a p b q f(a_1…a_p,b_1…b_q)=b_1b_2…b_{q−p}a_1b_{q−p+1}a_2…a_{p−1}b_{q−1}a_pb_q f(a1…ap,b1…bq)=b1b2…bq−pa1bq−p+1a2…ap−1bq−1apbq.
就统计长度为 x x x 的数的每一位数字之和,以及长度为 x x x 的数的个数,然后对于 f ( a , b ) f(a, b) f(a,b),枚举 a a a 的长度是 1 ∼ 10 1 \sim 10 1∼10 的时候,枚举 b b b 的长度是 1 ∼ 10 1 \sim 10 1∼10 的时候,统计一下每个数位的贡献就行了.
19. Problem - 1152C - Codeforces
给两个数字 a , b ( 1 ≤ a , b ≤ 1 0 9 ) a, b(1 \le a, b \le 10^9) a,b(1≤a,b≤109),求 k ≥ 0 k \ge 0 k≥0 使得 lcm ( a + k , b + k ) \operatorname{lcm}(a + k, b + k) lcm(a+k,b+k) 最小,若有多个满足的 k k k 输出最小的 k k k.
gcd ( a + k , b + k ) = gcd ( a + k , b − a ) = gcd ( a + k m o d b − a , b − a ) \gcd(a + k, b + k) = \gcd(a + k, b - a) = \gcd(a + k \bmod b - a, b - a) gcd(a+k,b+k)=gcd(a+k,b−a)=gcd(a+kmodb−a,b−a). 因此 gcd ( a + k , b + k ) \gcd(a + k, b + k) gcd(a+k,b+k) 是一个循环. 相当于求 i ∈ [ 0 , b − a − 1 ] , gcd ( i , b − a ) i \in [0, b - a - 1], \gcd(i, b - a) i∈[0,b−a−1],gcd(i,b−a) 的所有取值情况下 lcm ( a + k , b + k ) \operatorname{lcm}(a + k, b + k) lcm(a+k,b+k) 的最小值. 而 gcd ( i , b − a ) \gcd(i, b - a) gcd(i,b−a) 的所有取值即为 b − a b - a b−a 的所有因子. 然后算出来对应的 k k k 即可.
20. Problem - 1114C - Codeforces
给两个数字 n , b ( n ≤ 1 0 18 , b ≤ 1 0 12 ) n, b(n \le 10^{18}, b \le 10^{12}) n,b(n≤1018,b≤1012),问 n ! n! n! 在 b b b 进制下末尾有几个0.
把 b b b 质因数分解, b = p 1 c 1 p 2 c 2 . . . p k c k b = p_1^{c_1}p_2^{c_2}...p_k^{c_k} b=p1c1p2c2...pkck. 然后统计 n ! n! n! 分别有多少个质因子 p 1 , p 2 , . . . , p k p_1,p_2,...,p_k p1,p2,...,pk,假设有 c n t 1 , c n t 2 , . . . , c n t k cnt_1,cnt_2,...,cnt_k cnt1,cnt2,...,cntk 个。答案就是 min 1 ≤ i ≤ k c n t i c i \min\limits_{1 \le i \le k} \dfrac{cnt_i}{c_i} 1≤i≤kmincicnti
ll get(ll n, ll p)
{
ll res = 0;
while(n > 0)
{
res += n / p;
n /= p;
}
return res;
}
那个统计阶乘有多少个质因子的函数应该这样写,写成 for 循环肯能会溢出.
21. Problem - 1107D - Codeforces
给你一个
n
∗
n
n * n
n∗n 的矩阵,让你找能不能分成
k
∗
k
k*k
k∗k个方块,里面的数字全是
0
0
0 或
1
1
1.
n
≤
5200
n \le 5200
n≤5200.
每次把小矩阵的前缀和的信息存到左上角就行了,然后对比的时候就用这个信息.
22. Problem - 1081E - Codeforces
给出 N/2 个 偶数位的数,需要补充剩余 N/2 个奇数位的数,使得 每一位的前缀和都是完全平方数。
如果存在解,按顺序输出 N 个完整数字。
只需要顺次找到满足条件的最小的 x 1 , x 3 , . . . , x 2 n − 1 x_1, x_3, ...,x_{2n-1} x1,x3,...,x2n−1. 先找到满足 > x 2 > x_2 >x2 的最小的 m 1 2 m_1^2 m12,然后找到满足 > m 1 2 + x 4 > m_1^2 + x_4 >m12+x4 的最小的 m 3 m^3 m3,这样子顺次把 x 1 , x 3 . . . x_1,x_3... x1,x3... 找到. 因为总体满足单调性,因此不用二分,直接从小到大枚举即可.
23. Problem - 1061C - Codeforces
给一个长度为 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 的数列 a a a, a i ≤ 1 0 6 a_i \le 10^6 ai≤106. 问有多少个子序列 b 1 , b 2 , . . . , b k b_1, b_2,...,b_k b1,b2,...,bk,满足 ∀ i ∈ [ 1 , k ] , i ∣ b i \forall i \in [1, k], i \mid b_i ∀i∈[1,k],i∣bi.
枚举因数,假设枚举到了 d d d,如果 a i a_i ai 可以作为 b b b 的第 d d d 个元素,那么以 b d b_d bd 结尾的子序列的个数,是 1 ∼ i − 1 1 \sim i-1 1∼i−1 中以 b d − 1 b_{d-1} bd−1 结尾的子序列数量之和.
24. Problem - 1055C - Codeforces (再写)
第一个人的 lucky day 是 [ l 1 + k t 1 , r 1 + k t 1 ] [l_1 + kt_1,r_1 + kt_1] [l1+kt1,r1+kt1],第二个人的 lucky day 是 [ l 2 + k t 2 , r 2 + k t 2 ] [l_2 + kt_2, r_2 + kt_2] [l2+kt2,r2+kt2]. 问最多连续多少天,这些天都是两个人的 lucky day.
这个题就是让两个区间的起点尽可能地接近。若让 ∣ ( l 1 + k 1 t 1 ) − ( l 2 + k 2 t 2 ) ∣ |(l_1 + k_1t_1) -(l_2 + k_2t_2)| ∣(l1+k1t1)−(l2+k2t2)∣ 尽可能小,则 ∣ l 1 − l 2 + k gcd ( t 1 , t 2 ) ∣ |l_1 - l_2 + k\gcd(t_1,t_2)| ∣l1−l2+kgcd(t1,t2)∣ 尽可能小。分为下面四种情况
- l 1 ≥ l 2 l_1 \ge l_2 l1≥l2 且 l 1 + k 1 t 1 ≤ l 2 + k 2 t 2 l_1 + k_1t_1 \le l_2 + k_2t_2 l1+k1t1≤l2+k2t2
- l 1 ≥ l 2 l_1 \ge l_2 l1≥l2 且 l 1 + k 1 t 1 ≥ l 2 + k 2 t 2 l_1 + k_1t_1 \ge l_2 + k_2t_2 l1+k1t1≥l2+k2t2
- l 1 ≤ l 2 l_1 \le l_2 l1≤l2 且 l 1 + k 1 t 1 ≥ l 2 + k 2 t 2 l_1 + k_1t_1 \ge l_2 + k_2t_2 l1+k1t1≥l2+k2t2
- l 1 ≤ l 2 l_1 \le l_2 l1≤l2 且 l 1 + k 1 t 1 ≤ l 2 + k 2 t 2 l_1 + k_1t_1 \le l_2 + k_2t_2 l1+k1t1≤l2+k2t2
对于每种情况讨论答案即可. 如果想不清楚可以找些例子模拟一下.
25. Problem - 1034A - Codeforces
给 n ( n ≤ 3 × 1 0 5 ) n(n \le 3 \times 10^5) n(n≤3×105) 个数字, a i ≤ 1.5 × 1 0 7 a_i \le 1.5 \times 10^7 ai≤1.5×107. 问至少删掉多少个数字,才能让所有数字的最大公约数增大.
考虑唯一分解,让最大公约数增大,就是去掉最大公约数的限制,即对于出现过的 p p p,统计出现最小幂次的次数有多少,答案就是所有次数中最少的. 不过有次数为 0 0 0 的时候有点棘手。其实可以把 a i / gcd a_i / \gcd ai/gcd 质因数分解,然后再统计就是大于最小幂次的数字出现的次数。然后 n n n 减去这个数字就是最小幂次出现的次数.
26. Problem - 1030D - Codeforces
给定
n
,
m
,
k
n,m,k
n,m,k,构造一个三角形
0
≤
x
i
≤
n
,
0
≤
y
i
≤
m
0 \le x_i \le n, 0 \le y_i \le m
0≤xi≤n,0≤yi≤m. 使得其面积为
n
m
k
\dfrac{nm}{k}
knm.
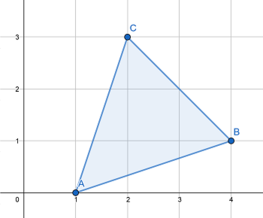
看这个例子,面积可以表示为
max
∣
x
i
−
x
j
∣
∗
max
∣
y
i
−
y
j
∣
−
1
2
(
∣
x
1
−
x
2
∣
∣
y
1
−
y
2
∣
+
∣
x
2
−
x
3
∣
∣
y
2
−
y
3
∣
+
∣
x
1
−
x
3
∣
∣
y
1
−
y
3
∣
)
\max|x_i - x_j| * \max|y_i - y_j| - \dfrac{1}{2}(|x_1 - x_2||y_1-y_2| + |x_2 - x_3||y_2 - y_3| + |x_1 - x_3||y_1 - y_3|)
max∣xi−xj∣∗max∣yi−yj∣−21(∣x1−x2∣∣y1−y2∣+∣x2−x3∣∣y2−y3∣+∣x1−x3∣∣y1−y3∣). 因此分母至多是2. 因此
n
m
k
\dfrac{nm}{k}
knm 化成最简分式后
k
≤
2
k \le 2
k≤2. 因此最后特判一些不合法条件后(
k
0
=
1
k_0 = 1
k0=1),构造一个直角三角形 (
(
0
,
0
)
,
(
n
′
,
0
)
,
(
0
,
m
′
)
(0,0), (n',0), (0, m')
(0,0),(n′,0),(0,m′)) 即可.
27. Problem - 1010C - Codeforces
给 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 个数字,问在 k ( k ≤ 1 0 5 ) k(k \le 10^5) k(k≤105) 进制下,这 n n n 个数字随意进行加法 (即 m 1 a 1 + m 2 a 2 + . . . + m n a n , m i ∈ [ 0 , ∞ ) m_1a_1+m_2a_2+ ... + m_na_n, m_i \in [0, \infty) m1a1+m2a2+...+mnan,mi∈[0,∞) ),末尾数字有多少种取值.
首先考虑只取一个数字的情况:即 m a i m o d k ma_i \bmod k maimodk 有多少种取值,其实就是求 gcd ( k , a 1 , a 2 , . . . , a n ) \gcd(k, a_1, a_2,...,a_n) gcd(k,a1,a2,...,an),设为 d d d;之后再求 d d d 与 a i a_i ai 的组合能够有多少种情况. 其实就是 a i x + d y ≡ gcd ( a i , d ) ( m o d k ) a_ix+dy\equiv \gcd(a_i, d) \pmod k aix+dy≡gcd(ai,d)(modk). 也是和 gcd ( a i , d ) \gcd(a_i,d) gcd(ai,d) 有关。注意这里由于有取模,一定可以让 x x x 和 y y y 都取到非负整数。
设 d 0 = gcd ( a i , d ) d_0 = \gcd(a_i,d) d0=gcd(ai,d),那么能得到的数字就是 0 , d 0 , 2 d 0 , 3 d 0 , . . . 0, d_0, 2d_0, 3d_0,... 0,d0,2d0,3d0,....
28. Problem - 963A - Codeforces (再写)
求
∑
i
=
0
n
s
i
a
n
−
i
b
i
\sum\limits_{i=0}^ns_ia^{n-i}b^i
i=0∑nsian−ibi,其中
1
≤
a
,
b
,
n
≤
1
0
9
1 \le a, b, n \le 10^9
1≤a,b,n≤109. 其中
s
s
s 是一个循环,循环节是
k
≤
1
0
5
k \le 10^5
k≤105.
∑
i
=
0
n
s
i
a
n
−
i
b
i
=
a
n
∑
i
=
0
n
s
i
(
b
a
)
i
\sum\limits_{i=0}^ns_ia^{n-i}b^i = a^n \sum\limits_{i=0}^{n}s_i (\dfrac{b}{a})^i
i=0∑nsian−ibi=ani=0∑nsi(ab)i. 就可以转化为等比数列求和了.
有坑!公比为1的时候不可以用求和公式。而且注意这里的公比是
(
b
a
)
k
(\dfrac{b}{a})^k
(ab)k.
a
b
≠
1
\dfrac{a}{b} \ne 1
ba=1 时,
(
b
a
)
k
(\dfrac{b}{a})^k
(ab)k 可能仍是1.
29. Problem - 959D - Codeforces
给一个长度为 n ( n ≤ 1 0 5 ) n(n \le 10^5) n(n≤105) 的序列 a a a, 2 ≤ a i ≤ 1 0 5 2 \le a_i \le 10^5 2≤ai≤105. 请构造一个字典序最小的序列 b b b,要求 b b b 的字典序不能小于 a a a; b i ≥ 2 b_i \ge 2 bi≥2; b b b 中所有数字两两互质.
两两互质就是把前面的每个数字都质因数分解,新的数字的质因子不可以出现过. 如果找到一个冲突的,那么就暴力每次增加1,直到成功为止。后面的数字就把没有出现过的质数从小到大写上去就行。不过注意这个题的质数要多筛很多,不能只筛到 1 0 5 10^5 105. 因为后面可能需要新增很多质数.
30. Problem - 894B - Codeforces
m
+
n
m + n
m+n 为奇数的时候,不妨设
n
n
n 为奇数
m
m
m 为偶数,假设每行每列都是奇数个-1.
n
n
n 行(奇数),每行奇数个-1,所有-1的总数是奇数。但是
m
m
m 列(偶数),每列奇数个 -1,共偶数个-1.
因此
n
+
m
n+m
n+m 时,无法凑出奇数个-1的情况,因此答案是0.
考虑在 n − 1 n-1 n−1 行 m − 1 m-1 m−1 列随意放数字,那么最后一行最后一列的方案是唯一确定了的。也就是说自由度只有 ( n − 1 ) ( m − 1 ) (n-1)(m-1) (n−1)(m−1) 个。因此方案总数为 2 ( n − 1 ) ( m − 1 ) 2^{(n-1)(m-1)} 2(n−1)(m−1).




















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








