命题

注意:有确定的真假含义不等同于已知其真假含义。
例:较大的偶数都可表为两个质数之和。
例:除地球外,别的星球上也存在生物。
原子命题(Primitive proposition):
由简单陈述句表示的判断。
命题逻辑规定:原子命题是不可再分的。
复合命题(Compound proposition):
一个或几个简单命题用联结词联结所构成的命题(复合陈述句)。
例:如果天气好,我就去散步。
例:2是偶数而3是奇数。
命题的表示

两个特殊的命题词:
命题常量:
T:永远表示真命题。
F:永远表示假命题。
T和F的两种含义:
命题常量。
命题的真值。
命题联结词
命题和原子命题常可通过一些联结词构成新命题,这种新命题叫复合命题。
否定词:┐(~,Negation)
设P表示命题,那么“P不真”是一个复合命题,记为┐P,叫做P的否定,读做“非P”。如果P是假,则┐P是真,反之亦然。
例子:
- 1.P: 4是质数。 ┐P: 4不是质数。
- 2.Q:这些都是男同学。 ┐Q:这些不都是男同学。
合取词:∧(Conjunction)
如果P和Q是命题,那么“P并且Q”是一个复合命题,记为P∧Q,称为P和Q的合取,读做“P与Q”或“P并且Q”。
析取词:∨(Disjunction)
如果P和Q是命题, 则“P或Q” 是一个复合命题, 记作P∨Q, 称为P和Q的析取, 读做“P或Q”。
注意:大致与自然语言中表示选择的“或”,“或者”类似,但自然语言中的或具有二义性,用“或”联结的命题,有时具有相容性,有时具有排斥性。

条件词:→(条件,Conditional)
如果P和Q是命题,那么“P蕴含Q”是一个复合命题,记为P→Q,称为条件式,读做“如果P,那么Q”或“P则Q”。运算对象P叫做前提,假设或前件,而Q叫做结论或后件。
注意:与自然语言中表示因果的“若… 则 …”、 “如果…则…”、“如果…那么…”、“只要…就…”等类似。
例子:
- 1 P: 天不下雨, Q: 草木枯黄。 P→Q: 如果天不下雨, 那么草木枯黄。
- 2 R: G是正方形, S: G的四边相等。 R→S: 如果G是正方形, 那么G的四边相等。
- 3 W: 桔子是紫色的, V: 大地是不平的。 W→V: 如果桔子是紫色的, 那么大地是不平的。

注意:在自然语言中,条件和结论往往有某种内在联系,并且往往表示若条件成立则结论也成立这样的推理关系,而在数理逻辑中,条件和结论不一定有内在联系,且若条件为假则条件式为真。
蕴含式P→Q可以用多种方式陈述:
- “若P, 则Q”
- “P是Q的充分条件”
- “Q是P的必要条件”
- “Q每当P” ;
- “P仅当Q”等。
例子:
- 令:P:天气好。 Q:我去公园。
- 如果天气好,我就去公园。P→Q
- 只要天气好,我就去公园。P→Q
- 天气好,我就去公园。P→Q
- 仅当天气好,我才去公园。Q→P
- 只有天气好,我才去公园。Q→P
- 我去公园,仅当天气好。Q→P
双条件词:↔(等值,Biconditional)
如果P和Q是命题, 那么“P等值于Q”是一个复合命题, 记为P↔Q, 称为双条件式(等值式), 读做“P当且仅当Q”、“P iff Q”或“P等值于Q”。
P↔Q也读做“P的充要条件是Q”。
有时“除非”也有互为因果的意义。
联结词的注意事项
熟练掌握这五个联结词在自然语言中所表示的含义(但要注意具体语言环境)以及它们的真值表的定义。
特别要注意“或”的二义性,即要区分给定的“或”是“可兼取的或”还是“不可兼取的或”。
特别要注意“→”的用法,它既表示“充分条件”也表示“必要条件”,即要弄清哪个作为前件,哪个作为后件。
联结词的优先级顺序:┐, ∧ , ∨ , → , ↔
命题公式与翻译
命题变元与命题公式

命题公式 wff(命题演算的合式公式,wellformed formula)
定义:
⑴ 单个命题词是个合式公式。
⑵ 若A是合式公式,则(┐A)是合式公式。
⑶ 若A和B是合式公式,则(A∧B),(A∨B),(A→B)和(A↔B)都是合式公式。
⑷ 当且仅当有限次地应用⑴,⑵,⑶所得到的含有命题变元、联结词和圆括号的符号串是合式公式。
此外,称逐次使用规则⑴,⑵,⑶的过程中所得到的命题公式为最后构成的命题公式的子公式。

命题符号化(翻译)


等价公式
真值表
设A(P1,P2,…,Pn) 是一个wff,P1,P2,…,Pn是出现于其中的全部命题变元。如果有一张表列出了在P1,P2,…,Pn 的所有2n种真值指派的每一种下,公式A对应的真值,则称此表为公式A的真值表。
- 按子公式列表
- 按逻辑联结词列表
注:
- 其中P1,P2,…,Pn按字典顺序排列
- 对应公式的每种指派,以二进制数升序或降序列出
- 命题公式不是命题
- 对应的真值指派可记为I=(P1’,P2 ’,…,Pn ’),其中Pi ’=0或1

等价公式


公式等价的证明
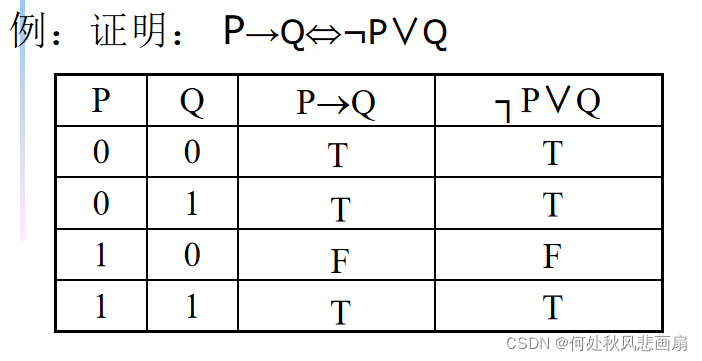
方法1:列真值表
方法2:等价变换
方法3:主范式


公式分类
重言式与矛盾式

重言式的证明方法:、
方法1:列真值表。
方法2:公式的等价变换,化简成”T”。
方法3:用公式的主析取范式。


蕴含式




其他联结词
联结词的扩充

一元联结词的个数:
1.一元联结词是联结一个命题变元的。
2.由一个命题变元P可构成4种不等价的命题公式。
3.相应的可定义出4个不同的一元联结词。

二元联结词的个数:
1.二元联结词联结两个命题变元。
2.由两个命题变元P,Q可构成16种不等价的命题公式。
3.相应的可定义出16个不同的二元联结词。

联结词组
{ ┐, ∨ } 是最小联结词组。
{ ┐, ∧ } 是最小联结词组 。
{ ↑ } 是最小联结词组。
{ ↓ } 是最小联结词组。
对偶与范式
定义1:设有公式A, 其中仅有联结词∧ , ∨ , ┐。在A中将 ∧ , ∨ , T , F分别换以∨ , ∧ , F , T得公式A*,则A*称为A的对偶(公)式。
例 :A = P∨F , A*=?
解: A*= P∧T
对偶原理




范式
命题逻辑中,将公式化成主范式可使公式有唯一表示形式。
析取范式

合取范式

析取范式与合取范式的求法


主析取范式和主合取范式
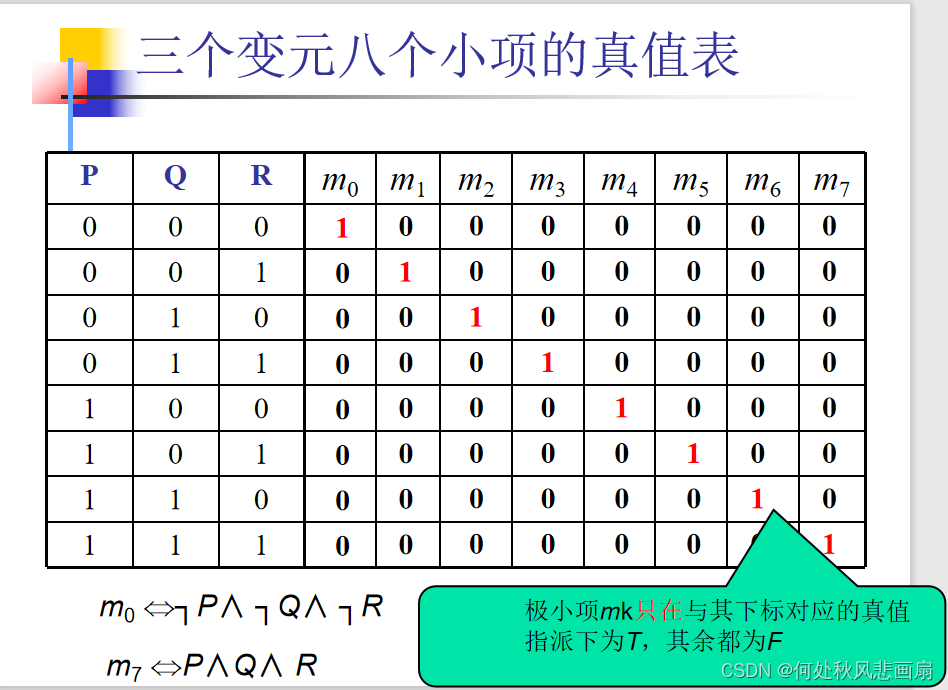
极小项




主析取范式
定义:一个仅由小项的析取组成的公式, 如果与给定的命题公式A等价, 则称它是A的主析取范式。
定理:一个公式A(P1, P2, …, Pn)的真值表中,使A为T的指派所对应的诸小项之析取,即为A的主析取范式。



极大项



主合取范式
定义:一个仅由大项的合取组成的公式, 如果与给定的命题公式A等价, 则称它是A的主合取范式。
定理:在公式A的真值表中,使A为F的指派所对应的诸大项的析取,即为A的主合取范式。


主析取范式和主合取范式的关系
一个命题公式的主析取范式和主合取范式紧密相关。
在它们的简记式中, 代表小项和大项的足标是互补的, 即两者一起构成0, 1, 2, … , 2^n - 1诸数。
主析(合)取范式的应用
(1)求公式的成真/成假赋值:
若公式A中含有n个命题变元,且A的主析取范式含s个小项,则A有s个成真赋值,有2^n - s个成假赋值。(即主析取范式中的小项对应的编码是公式A的成真赋值;反之主合取范式中的大项对应的编码是公式A的成假赋值)。
(2)判断公式的类型:
设公式A中含有n个命题变元,则:
- A为重言式⇔A的主析取范式含全部2^n个小项。
- A为矛盾式⇔A的主析取范式不含任何小项,记A的主析取范式为0。
- A为可满足式⇔A的主析取范式至少含一个小项。
- A为矛盾式⇔A的主合取范式含全部2^n个大项。
- A为重言式⇔A的主合取范式不含任何大项,记A的主合取范式为1 。
- A为可满足式⇔A的主合取范式中大项的个数一定小于2^n 。
(3)判断两个命题是否等价:
设公式A、B中共含有n个命题变元,按n个命题变元求出A、B的主析(合)取范式A’、B’ 。若A’=B’,则A⇔B,否则A、B不等价。
(4)解决实际问题:
例:某科研所有三名青年高级工程师A,B,C。所里要选派他们中的1到2人出国进修,由于所里工作的需要,选派时必须满足以下条件:
①若A去,则C也可以去;
②若B去,则C不能去;
③若C不去,则A或B可以去。
问:所里应如何选派他们?

推理理论
常用的证明方法


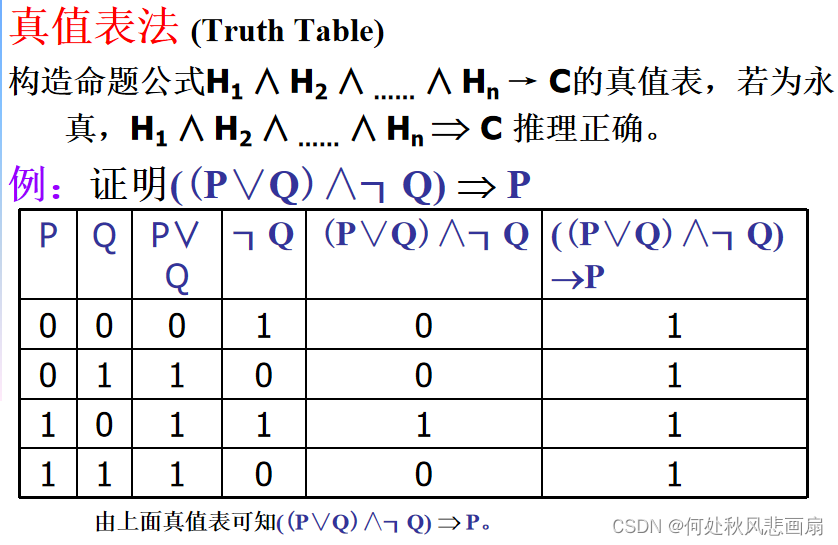
真值表法
直接证明法

间接证明法


由证(H1∧H2∧…∧Hk∧R)→C永真而证得(H1∧H2∧Hk)→(R→C)永真的证明方法, 称为附加前提证明法或CP规则。



附录



































 7601
7601

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








