正态性检验（Shapiro-Wilk test检验和kstest检验）

正态分布又称高斯分布（Gaussian distribution）​。若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N(μ,σ2)，其中期望值μ决定了其位置，标准差σ决定了分布的幅度。当μ=0,σ=1时的正态分布就是标准正态分布。有相当多的统计程序对数据要求比较严格，它们只有在变量服从或者近似服从正态分布的时候才是有效的，所以在对整理收集的数据进行预处理的时候需要对它们进行正态检验。

数据：

1 Shapiro-Wilk test检验

使用Shapiro-Wilk test检验数据是否服从正态分布的代码如下：

import pandas as pd#载入pandas模块，并简称为pd
import numpy as np#载入numpy模块，并简称为np

from scipy import stats#载入stats模块


data=pd.read_csv(r'数据4.1.csv')
#Shapiro-Wilk test检验
Ho = '数据服从正态分布'#定义原假设
Ha = '数据不服从正态分布'#定义备择假设
alpha = 0.05#定义显著性P值
def normality_check(data):
    for columnName, columnData in data.items():
        print("Shapiro test for {columnName}".format(columnName=columnName))
        res = stats.shapiro(columnData)
        pValue = round(res[1], 2)
        if pValue > alpha:
            print("pvalue = {pValue} > {alpha}. 不能拒绝原假设. {Ho}".format(pValue=pValue, alpha=alpha, Ho=Ho))
        else:
            print("pvalue = {pValue} <= {alpha}. 拒绝原假设. {Ha}".format(pValue=pValue, alpha=alpha, Ha=Ha))
normality_check(data)

 结果：

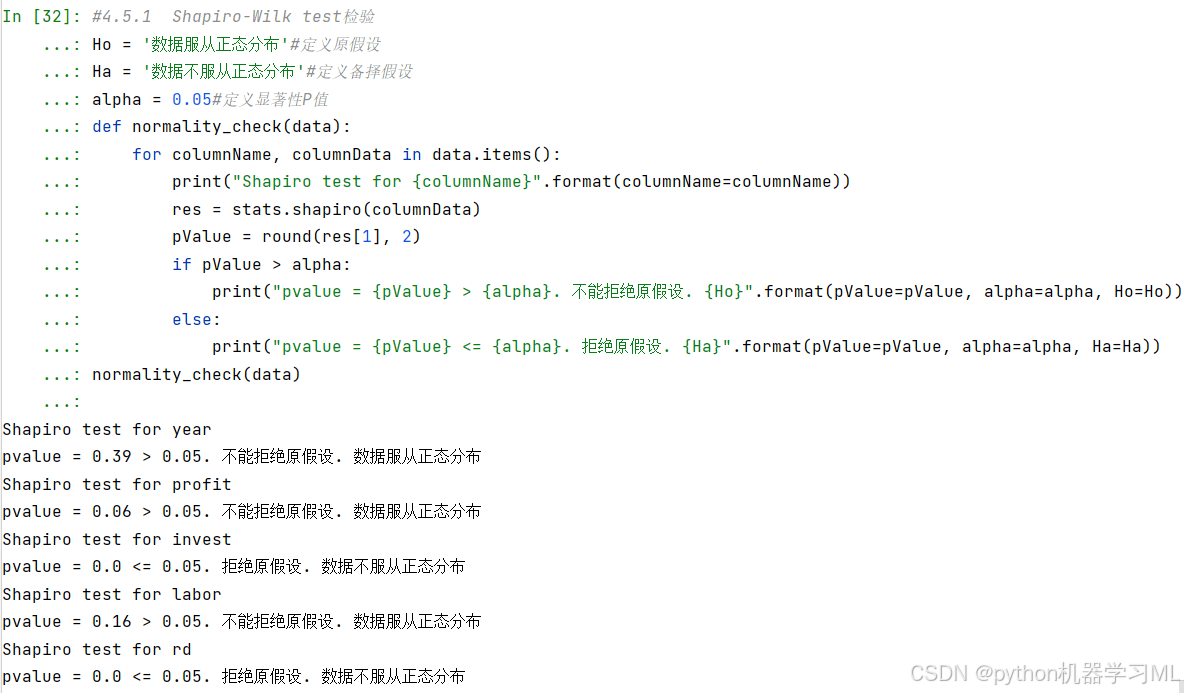综上所述，根据Shapiro-Wilk test检验结果，变量year、profit、labor服从正态分布，invest、rd不服从正态分布。

 

 说明：

1. 首先定义了原假设 Ho 和备择假设 Ha，以及显著性水平 alpha 为 0.05。

   • 原假设 Ho 表示数据服从正态分布。
   • 备择假设 Ha 表示数据不服从正态分布。
   • 显著性水平 alpha 通常用于判断是否拒绝原假设，一般取值较小，这里取 0.05 表示在 5% 的显著性水平下进行检验。

2. 定义了一个名为 normality_check 的函数，该函数接受一个参数 data，通常这个参数是一个字典或者类似的数据结构，其中包含不同的数据集，每个数据集可以通过一个键（比如列名）来访问。

3. 在 normality_check 函数内部，使用 for 循环遍历 data 中的每一个键值对，其中 columnName 是键（通常是列名），columnData 是对应的值（通常是一列数据）。

   • print("Shapiro test for {columnName}".format(columnName=columnName)) 这行代码打印出正在进行 Shapiro-Wilk 检验的列名。

   • res = stats.shapiro(columnData) 调用 stats.shapiro 函数对当前列的数据进行 Shapiro-Wilk 检验，这个函数会返回一个包含检验统计量和 p 值的元组。

   • pValue = round(res[1], 2) 从元组中取出 p 值，并将其保留两位小数。

   • if pValue > alpha: 如果 p 值大于显著性水平 alpha，则表示不能拒绝原假设，即数据可能服从正态分布。打印出相应的信息，包括 p 值、显著性水平和原假设的内容。

   • else: 如果 p 值小于等于显著性水平 alpha，则拒绝原假设，即数据不服从正态分布。打印出相应的信息，包括 p 值、显著性水平和备择假设的内容。

4. 最后，调用 normality_check(data) 函数，传入要进行正态性检验的数据，开始执行整个检验过程。

使用 Shapiro-Wilk 检验来判断给定数据集中的每一列数据是否服从正态分布，并根据检验结果打印出相应的结论。

2 kstest检验

使用kstest检验数据是否服从正态分布的代码如下：

# 使用kstest检验数据是否服从正态分布
Ho = '数据服从正态分布'#定义原假设
Ha = '数据不服从正态分布'#定义备择假设
alpha = 0.05#定义显著性P值
def normality_check(data):
    for columnName, columnData in data.items():
        print("kstest for {columnName}".format(columnName=columnName))
        res = stats.kstest(columnData,'norm')
        pValue = round(res[1], 2)
        if pValue > alpha:
            print("pvalue = {pValue} > {alpha}. 不能拒绝原假设. {Ho}".format(pValue=pValue, alpha=alpha, Ho=Ho))
        else:
            print("pvalue = {pValue} <= {alpha}. 拒绝原假设. {Ha}".format(pValue=pValue, alpha=alpha, Ha=Ha))
normality_check(data)

结果：

综上所述，根据kstest检验结果，变量year、profit、invest、labor、rd均不服从正态分布。综合两种检验结果，我们可以认为year、profit、invest、labor、rd均不服从正态分布。

说明：

1. 首先定义了原假设 Ho、备择假设 Ha 和显著性水平 alpha：

   • Ho 表示数据服从正态分布。
   • Ha 表示数据不服从正态分布。
   • alpha 设置为 0.05，通常用于判断是否拒绝原假设，即在 5% 的显著性水平下进行检验。

2. 定义了一个名为 normality_check 的函数，该函数接受一个参数 data，通常这个参数是一个字典或者类似的数据结构，其中包含不同的数据集，每个数据集可以通过一个键（比如列名）来访问。

3. 在 normality_check 函数内部：

   • 使用 for 循环遍历 data 中的每一个键值对，其中 columnName 是键（通常是列名），columnData 是对应的值（通常是一列数据）。
   • print("kstest for {columnName}".format(columnName=columnName)) 打印出正在进行 Kolmogorov-Smirnov 检验的列名。
   • res = stats.kstest(columnData, 'norm') 使用 scipy.stats 模块中的 kstest 函数对当前列的数据进行检验。第一个参数 columnData 是要检验的数据，第二个参数 'norm' 表示检验其是否服从正态分布。这个函数会返回一个包含检验统计量和 p 值的元组。
   • pValue = round(res[1], 2) 从元组中取出 p 值，并将其保留两位小数。
   • 如果 pValue > alpha，表示 p 值大于显著性水平，此时不能拒绝原假设，打印出相应的信息，包括 p 值、显著性水平和原假设的内容。
   • 如果 pValue <= alpha，表示 p 值小于等于显著性水平，此时拒绝原假设，打印出相应的信息，包括 p 值、显著性水平和备择假设的内容。

4. 最后，调用 normality_check(data) 函数，传入要进行正态性检验的数据，开始执行整个检验过程。

使用 Kolmogorov-Smirnov 检验来判断给定数据集中的每一列数据是否服从正态分布，并根据检验结果打印出相应的结论。