几种插值方法在一维和二维图像插值上的比较

已于 2024-07-22 23:17:55 修改
阅读量2.3k 收藏 24
点赞数 48
文章标签： 算法
于 2024-07-21 04:03:30 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_45938795/article/details/140478837
版权

目录

Introduction

线性插值，三次插值，样条插值，自适应接触有理插值在一维插值上的比较

双线性插值，双三次插值，双样条插值，双自适应接触有理插值在二维插值上的比较

附录

Introduction

       插值是一种在数学和计算机科学领域中常见的技术，它允许我们通过已知数据点的值来推断出在这些数据点之间的值。

       常用的插值方法包括：线性插值，三次插值和样条插值，这里还介绍一种自适应接触有理插值方法。其中线性插值仅依赖于临近两个数据点，其余插值方法均被设计成依赖临近四个数据点。以上插值方法均可用于一维，二维和三维插值中，这里将讨论一维和二维插值。

       插值过程可简单认为是临近数据点的加权求和过程，这里以|X|表示用于插值的格点与目标插值点的距离。

       所使用的线性插值权值函数表达如下：

       I(X)=\begin{cases} & \text 1-|X|\quad|X|\leqslant 1 \\ & \text 0 \quad\quad\quad \ \ 1< |X| \end{cases}

       

       所使用的三次插值权值函数表达如下：

       当选择Catmull-Rom cubic为三次插值方法时，下式中的a = -0.5.

       I(X)=\begin{cases} & \text(a+2)|X|^3-(a+3)|X|^2+1\quad|X|\leqslant 1 \\ & \text a|X|^3-5a|X|^2+8a|X|-4a \ \quad1< |X|\leqslant 2 \\ & \text 0 \qquad \qquad \qquad \qquad \qquad \qquad \quad \ |X|\geqslant 2 \end{cases}

       所使用的样条插值为三次B样条插值，其权值表达式如下：

       I(X)=\begin{cases} & \frac{1}{2}|X|^3 -|X|^2+ \frac{2}{3} \quad \quad \quad \quad \quad|X|\leqslant 1\\ & -\frac{1}{6}|X|^3 +|X|^2-2|X|+\frac{4}{3} \quad 1< |X|\leqslant 2 \\ & 0 \qquad \qquad \qquad \qquad \qquad \qquad 2< |X| \end{cases}

       所使用的自适应接触有理插值方法的权值函数如下所示：

       I(X)=\begin{cases} & \frac{-0.168|X|^2-0.9129|X|+1.0808}{|X|^2-0.8319|X|+1.0808} \quad\quad |X|\leqslant 1 \\ & \frac{0.1953|X|^2-0.5858|X|+0.3905}{|X|^2-2.4402|X|+1.7676} \quad\quad \ 1< |X|\leqslant 2 \\ & 0 \qquad\qquad\qquad\qquad\qquad\quad \ \ 2< |X| \end{cases}

       下面是各个插值方法的权值函数与Sinc函数的比较。通常情况下认为Sinc函数是理想插值核函数，但其在空间域上不存在紧凑集，因此一般将其在空间域进行裁剪。但裁剪后将破坏sinc函数的原始频谱特性，上述几种插值方法在时域和频域下的比较如下所示：

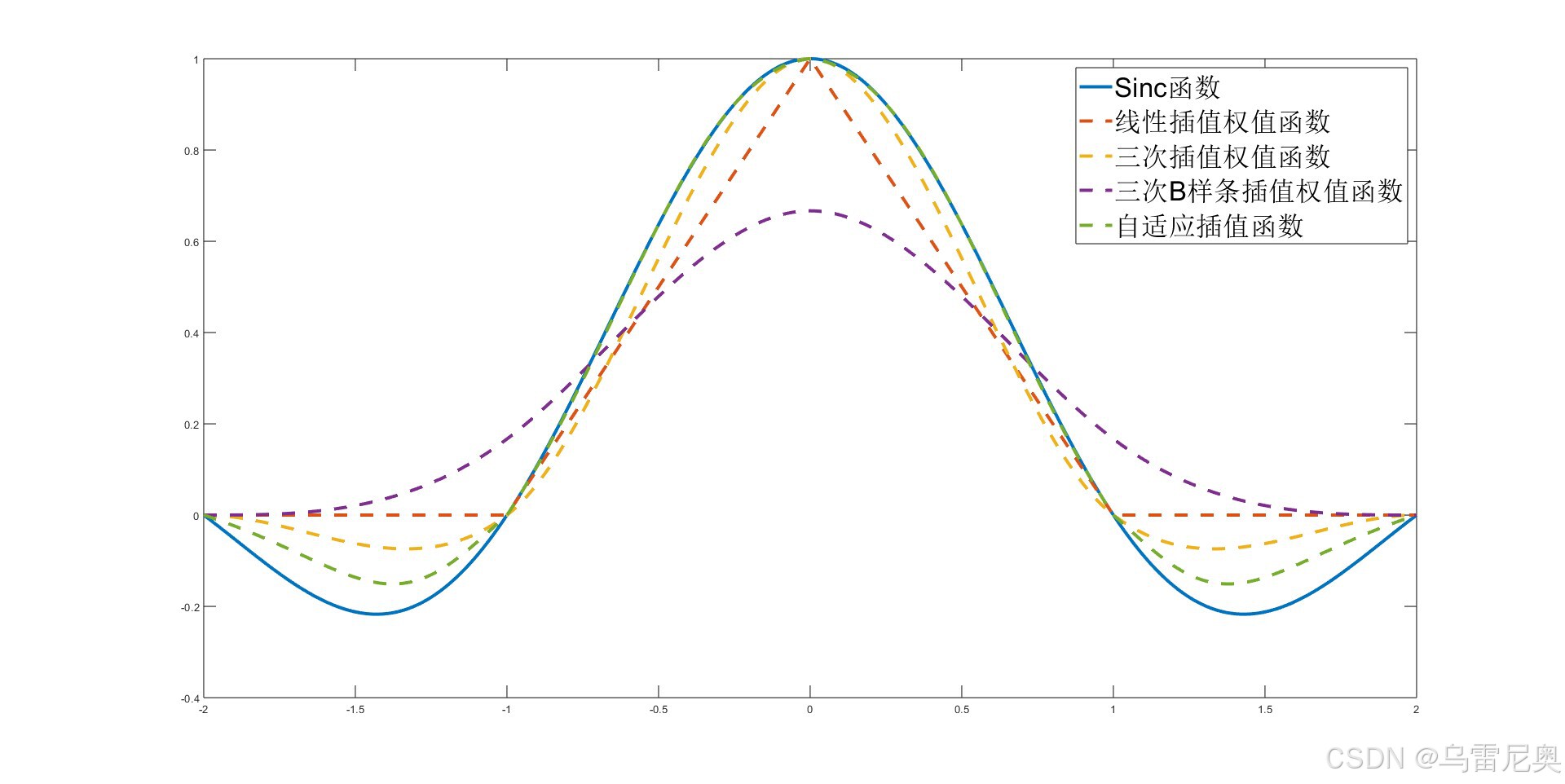
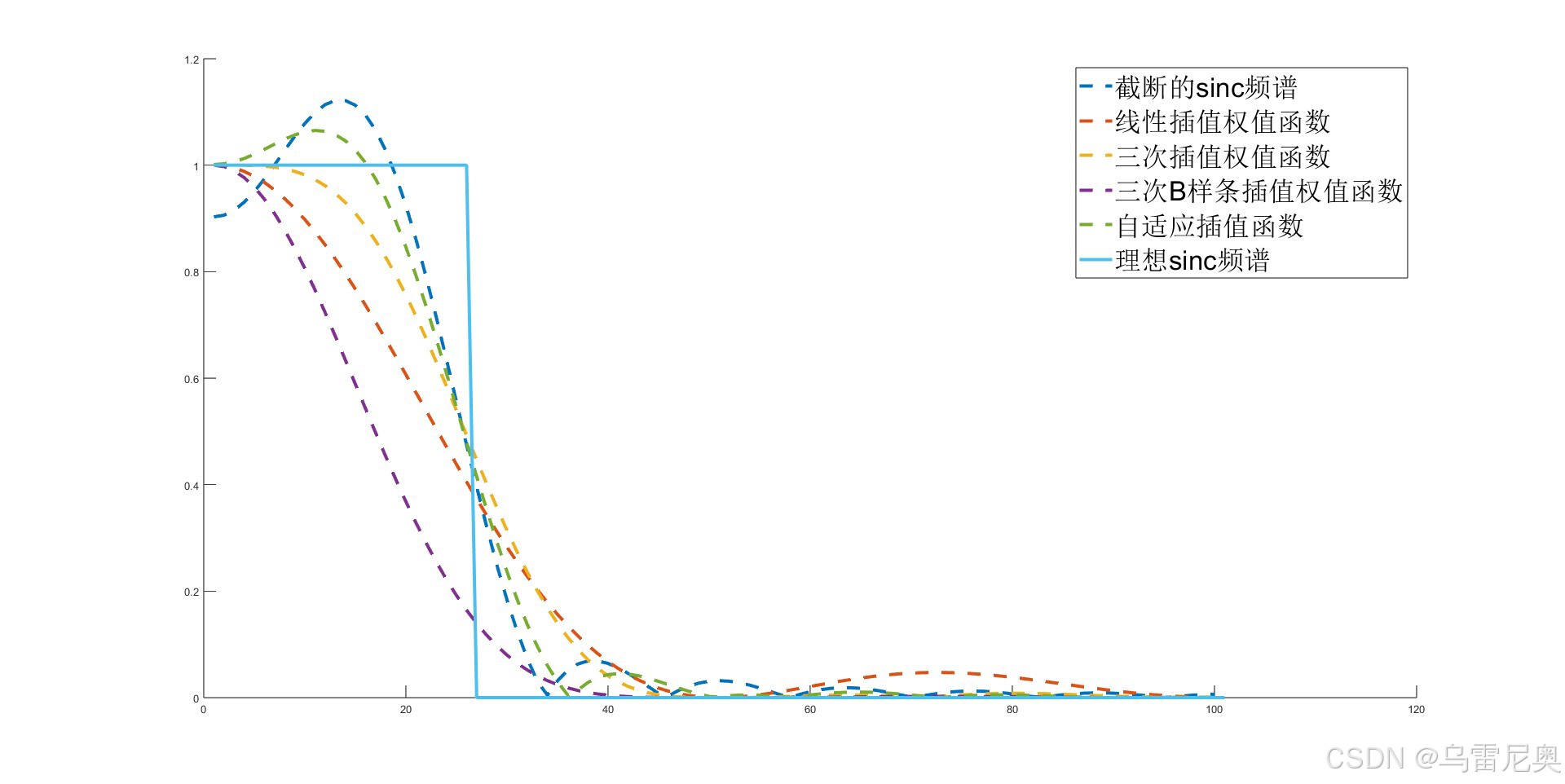
线性插值，三次插值，样条插值，自适应接触有理插值在一维插值上的比较

       这里将展示上述几种插值方法在一维数据上插值结果的比较。

       图示为原始数据向左偏移 3.25 个单位后的波形。可以观察到原始波形中正弦部分频率较低，插值效果较好，方波部分含有高频谐波，插值效果较差。频域相移也是时域插值的一个手段，这里也进行了比较。

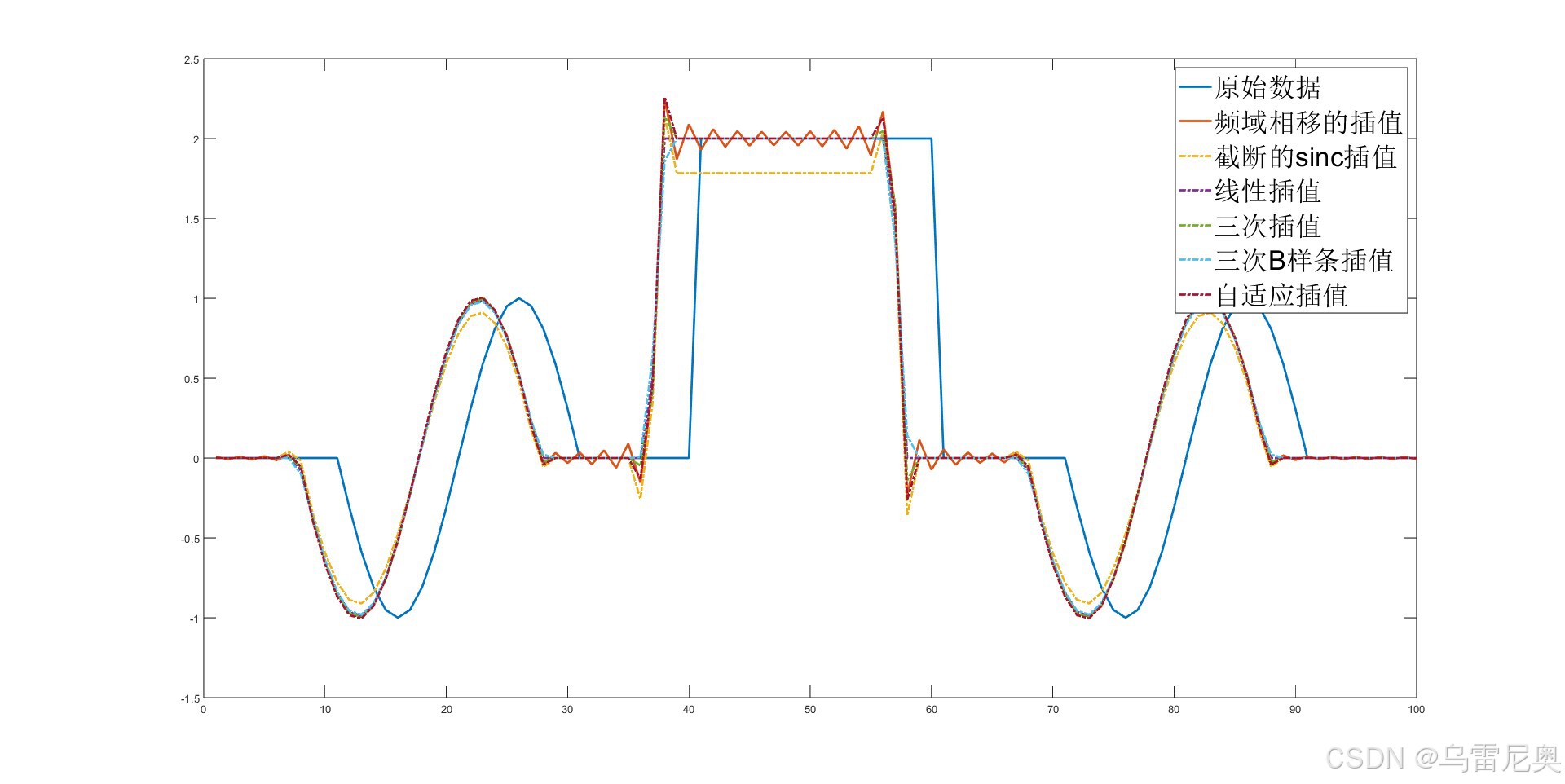
         总结而言，各种方法均难以应对高频信息的插值，且插值权重函数在频谱图中的高频成分越多，时域插值时在高频区域“抖动”越明显。

       下面是一维插值过程的Matlab脚本：

clc;
clear;
close all;

N_Original = 100;
fData_Original = zeros(1, N_Original);

% cos波形
f0 = 1;
fs = 20;
N_cos = 20;
n = 0 : 1 : N_cos - 1;
cos_y = cos(2 * pi * f0 * n / fs + pi / 2);

% 方波
N_square = 20;
Square_y = zeros(1, N_square);
Square_y(:) = 2;

N_interval = 10
fData_Original = [zeros(1, N_interval), cos_y, zeros(1, N_interval), Square_y, zeros(1, N_interval), cos_y, zeros(1, N_interval)];
fData_Original_Extend = [fData_Original(1), fData_Original, fData_Original(end)];


% 插值目标
fShift = 3.25;
nInterpolationNum = N_Original;           % 插值基数据点数
fs = 1;                                   % 采样率默认为1


% 频域相移实现时域插值
fft_fData = fft(fData_Original);

for k = 1: (nInterpolationNum / 2 + 1)
    w(k) = exp(2i * pi * (k - 1) * fs / nInterpolationNum * fShift);
end

fft_fData_transform(1:(nInterpolationNum / 2 + 1))  = fft_fData(1:(nInterpolationNum / 2 + 1))  .* w; 
for k = (nInterpolationNum/2 + 2): nInterpolationNum
    fft_fData_transform(k) = complex(real(fft_fData_transform(nInterpolationNum + 2 - k)),  - imag(fft_fData_transform(nInterpolationNum + 2 - k)));
end

ifft_fData_transform = ifft(fft_fData_transform);
ifft_fData_transform_real = real(ifft_fData_transform);


% 截断的sinc插值，三次插值，三次B样条插值，自适应插值
Sinc_interp_fData = zeros(nInterpolationNum, 1);
Cubic_interp_fData = zeros(nInterpolationNum, 1);
Cubic_Bspline_interp_fData = zeros(nInterpolationNum, 1);
Adapt_interp_fData = zeros(nInterpolationNum, 1);
for i = 1 : nInterpolationNum
    base_index = i + fShift;
    pre_interp_base_index_2 = floor(base_index) + 1;
    pre_interp_base_index_1 = pre_interp_base_index_2 - 1;
    pos_interp_base_index_2 = pre_interp_base_index_2 + 1;
    pos_interp_base_index_1 = pos_interp_base_index_2 + 1;
    if (pre_interp_base_index_2 > nInterpolationNum + 1)
        pre_interp_base_index_2 = nInterpolationNum + 1;
    end
    if (pre_interp_base_index_1 > nInterpolationNum + 1)
        pre_interp_base_index_1 = nInterpolationNum + 1;
    end
    if (pos_interp_base_index_1 > nInterpolationNum + 1)
        pos_interp_base_index_1 = nInterpolationNum + 1;
    end
    if (pos_interp_base_index_2 > nInterpolationNum + 1)
        pos_interp_base_index_2 = nInterpolationNum + 1;
    end
    delta_Pre_X_2 = base_index - floor(base_index);
    delta_Pre_X_1 = delta_Pre_X_2 + 1;
    delta_Pos_X_2 = 1 - delta_Pre_X_2;
    delta_Pos_X_1 = delta_Pos_X_2 + 1;
    
    % 截断的sinc插值
    Sinc_interp_fData(i) = sinc(delta_Pre_X_2) * fData_Original_Extend(pre_interp_base_index_2) + ...
                           sinc(delta_Pre_X_1) * fData_Original_Extend(pre_interp_base_index_1) + ...
                           sinc(delta_Pos_X_2) * fData_Original_Extend(pos_interp_base_index_2) + ...
                           sinc(delta_Pos_X_1) * fData_Original_Extend(pos_interp_base_index_1);

    % 三次插值
    W_delta_Pre_X_2 = 1.5 * delta_Pre_X_2^3 - 2.5 * delta_Pre_X_2^2 + 1;
    W_delta_Pre_X_1 = -0.5 * delta_Pre_X_1^3 + 2.5 * delta_Pre_X_1^2 - 4 * delta_Pre_X_1 + 2;
    W_delta_Pos_X_2 = 1.5 * delta_Pos_X_2^3 - 2.5 * delta_Pos_X_2^2 + 1;
    W_delta_Pos_X_1 = -0.5 * delta_Pos_X_1^3 + 2.5 * delta_Pos_X_1^2 - 4 * delta_Pos_X_1 + 2;
    
    Cubic_interp_fData(i) = W_delta_Pre_X_1 * fData_Original_Extend(pre_interp_base_index_1) + ...
                            W_delta_Pre_X_2 * fData_Original_Extend(pre_interp_base_index_2) + ...
                            W_delta_Pos_X_1 * fData_Original_Extend(pos_interp_base_index_1) + ...
                            W_delta_Pos_X_2 * fData_Original_Extend(pos_interp_base_index_2);

    % 三次B样条插值
    W_delta_Pre_X_1 = -(1 / 6) * delta_Pre_X_1^3 + delta_Pre_X_1^2 - 2 * delta_Pre_X_1 + (4 / 3);
    W_delta_Pre_X_2 = 0.5 * delta_Pre_X_2^3 - delta_Pre_X_2^2 + (2 / 3);
    W_delta_Pos_X_2 = 0.5 * delta_Pos_X_2^3 - delta_Pos_X_2^2 + (2 / 3);
    W_delta_Pos_X_1 = -(1 / 6) * delta_Pos_X_1^3 + delta_Pos_X_1^2 - 2 * delta_Pos_X_1 + (4 / 3);
    
    Cubic_Bspline_interp_fData(i) = W_delta_Pre_X_1 * fData_Original_Extend(pre_interp_base_index_1) + ...
                                    W_delta_Pre_X_2 * fData_Original_Extend(pre_interp_base_index_2) + ...
                                    W_delta_Pos_X_1 * fData_Original_Extend(pos_interp_base_index_1) + ...
                                    W_delta_Pos_X_2 * fData_Original_Extend(pos_interp_base_index_2);

    % 自适应插值
    W_delta_Pre_X_1 = (0.1953 * delta_Pre_X_1^2 - 0.5858 * delta_Pre_X_1 + 0.3905) / (delta_Pre_X_1^2 - 2.4402 * delta_Pre_X_1 + 1.7676);
    W_delta_Pre_X_2 = (-0.168 * delta_Pre_X_2^2 - 0.9129 * delta_Pre_X_2 + 1.0808) / (delta_Pre_X_2^2 - 0.8319 * delta_Pre_X_2 + 1.0808);
    W_delta_Pos_X_2 = (-0.168 * delta_Pos_X_2^2 - 0.9129 * delta_Pos_X_2 + 1.0808) / (delta_Pos_X_2^2 - 0.8319 * delta_Pos_X_2 + 1.0808);
    W_delta_Pos_X_1 = (0.1953 * delta_Pos_X_1^2 - 0.5858 * delta_Pos_X_1 + 0.3905) / (delta_Pos_X_1^2 - 2.4402 * delta_Pos_X_1 + 1.7676);

    Adapt_interp_fData(i) = W_delta_Pre_X_1 * fData_Original_Extend(pre_interp_base_index_1) + ...
                                    W_delta_Pre_X_2 * fData_Original_Extend(pre_interp_base_index_2) + ...
                                    W_delta_Pos_X_1 * fData_Original_Extend(pos_interp_base_index_1) + ...
                                    W_delta_Pos_X_2 * fData_Original_Extend(pos_interp_base_index_2);
end


% 线性插值
Line_interp_fData = zeros(nInterpolationNum, 1);
for i = 1 : nInterpolationNum
    base_index = i + fShift;
    pre_interp_base_index = floor(base_index);
    pos_interp_base_index = pre_interp_base_index + 1;
    if (pre_interp_base_index > nInterpolationNum)
        pre_interp_base_index = nInterpolationNum;
    end
    if (pos_interp_base_index > nInterpolationNum)
        pos_interp_base_index = nInterpolationNum;
    end

    delta_X = base_index - floor(base_index);

    Line_interp_fData(i) = (1 - delta_X) * fData_Original(pre_interp_base_index) + delta_X * fData_Original(pos_interp_base_index);
end


figure(1),
plot(fData_Original, 'LineWidth', 2);
hold on,
plot(ifft_fData_transform_real, 'LineWidth', 2);
hold on,
plot(Sinc_interp_fData, '-.', 'LineWidth', 2);
hold on,
plot(Line_interp_fData, '-.', 'LineWidth', 2);
hold on,
plot(Cubic_interp_fData, '-.', 'LineWidth', 2);
hold on,
plot(Cubic_Bspline_interp_fData, '-.', 'LineWidth', 2);
hold on,
plot(Adapt_interp_fData, '-.', 'LineWidth', 2);
legend('原始数据','频域相移的插值', '截断的sinc插值', '线性插值','三次插值','三次B样条插值','自适应插值', 'fontsize', 25);

双线性插值，双三次插值，双样条插值，双自适应接触有理插值在二维插值上的比较

这里将展示上述几种插值方法在二维图像上插值结果的比较。

       图示为原图放大 2倍 后的图像。可以观察到，插值权重函数频谱图中，高频成分越多，插值结果保留的高频信息越丰富，下图所示双自适应有理接触式插值结果的图像最锐利。

下面是二维插值过程的Matlab脚本：

clc;
clear;
close all;

% 读取图片
imageData = imread('qq.png');
imageData = rgb2gray(imageData);

figure(1);
imshow(imageData);
title('原图', 'fontsize', 17);

% 原始图片维度
dims = size(imageData);
rowCount = dims(1); % 矩阵的行数
colCount = dims(2); % 矩阵的列数

% 目标插值后图片维度
Ratio = 2;
Interp_rowCount = Ratio * rowCount;
Interp_colCount = Ratio * colCount;

% 图片延拓一个像素（延拓方式为取边缘像素点值）
Extend_imageData = double(padarray(imageData, [1 1], 'replicate'));

% 图片延拓两个像素（延拓方式为取边缘像素点值）
Extend_Bi_imageData = double(padarray(imageData, [2 2], 'replicate'));


% 线性插值
Liner_Interp_imageData = zeros(Interp_rowCount, Interp_colCount);
for i = 1 : Interp_rowCount
    for j = 1 : Interp_colCount
        Index_X_Target = j;
        Index_Y_Target = i;

        First_Ori_Index_in_Target = (Ratio + 1) / 2;
        Index_X_Ori = floor((Index_X_Target - First_Ori_Index_in_Target) / Ratio + 1);
        Index_Y_Ori = floor((Index_Y_Target - First_Ori_Index_in_Target) / Ratio + 1);

        % 目标点左上角网格点的坐标
        Index_X_Ori_in_Target = First_Ori_Index_in_Target + (Index_X_Ori - 1) * Ratio;
        Index_Y_Ori_in_Target = First_Ori_Index_in_Target + (Index_Y_Ori - 1) * Ratio;

        % 双线性插值————权重函数
        delta_X = (Index_X_Target - Index_X_Ori_in_Target) / Ratio;
        delta_Y = (Index_Y_Target - Index_Y_Ori_in_Target) / Ratio;

        Pre_Index_X_in_Extend = Index_X_Ori + 1;
        Pos_Index_X_in_Extend = Pre_Index_X_in_Extend + 1;
        Pre_Index_Y_in_Extend = Index_Y_Ori + 1;
        Pos_Index_Y_in_Extend = Pre_Index_Y_in_Extend + 1;

        Value_Target = (1 - delta_X) * (1 - delta_Y) * Extend_imageData(Pre_Index_Y_in_Extend, Pre_Index_X_in_Extend) +...
                       (1 - delta_X) * delta_Y * Extend_imageData(Pos_Index_Y_in_Extend, Pre_Index_X_in_Extend) +...
                       delta_X * (1 - delta_Y) * Extend_imageData(Pre_Index_Y_in_Extend, Pos_Index_X_in_Extend) +...
                       delta_X * delta_Y * Extend_imageData(Pos_Index_Y_in_Extend, Pos_Index_X_in_Extend);

        Liner_Interp_imageData(i, j) = Value_Target;
    end
end

figure(3);
imshow(uint8(Liner_Interp_imageData));
title('双线性插值结果', 'fontsize', 17);


% 双三次插值
Bicubic_Interp_imageData = zeros(Interp_rowCount, Interp_colCount);
for i = 1 : Interp_rowCount
    for j = 1 : Interp_colCount
        Index_X_Target = j;
        Index_Y_Target = i;

        First_Ori_Index_in_Target = (Ratio + 1) / 2;
        Index_X_Ori = floor((Index_X_Target - First_Ori_Index_in_Target) / Ratio + 1);
        Index_Y_Ori = floor((Index_Y_Target - First_Ori_Index_in_Target) / Ratio + 1);

        % 目标点左上角网格点的坐标
        Index_X_Ori_in_Target = First_Ori_Index_in_Target + (Index_X_Ori - 1) * Ratio;
        Index_Y_Ori_in_Target = First_Ori_Index_in_Target + (Index_Y_Ori - 1) * Ratio;

        delta_Pre_X_1 = (Index_X_Target - (Index_X_Ori_in_Target - Ratio)) / Ratio;
        delta_Pre_X_2 = (Index_X_Target - Index_X_Ori_in_Target) / Ratio;
        delta_Pos_X_2 = 1 - delta_Pre_X_2;
        delta_Pos_X_1 = delta_Pos_X_2 + 1;
        delta_Pre_Y_1 = (Index_Y_Target - (Index_Y_Ori_in_Target - Ratio)) / Ratio;
        delta_Pre_Y_2 = (Index_Y_Target - Index_Y_Ori_in_Target) / Ratio;
        delta_Pos_Y_2 = 1 - delta_Pre_Y_2;
        delta_Pos_Y_1 = delta_Pos_Y_2 + 1;


        % 双三次插值————权重函数
        W_delta_Pre_X_1 = -0.5 * delta_Pre_X_1^3 + 2.5 * delta_Pre_X_1^2 - 4 * delta_Pre_X_1 + 2;
        W_delta_Pre_X_2 = 1.5 * delta_Pre_X_2^3 - 2.5 * delta_Pre_X_2^2 + 1;
        W_delta_Pos_X_2 = 1.5 * delta_Pos_X_2^3 - 2.5 * delta_Pos_X_2^2 + 1;
        W_delta_Pos_X_1 = -0.5 * delta_Pos_X_1^3 + 2.5 * delta_Pos_X_1^2 - 4 * delta_Pos_X_1 + 2;
        W_delta_Pre_Y_1 = -0.5 * delta_Pre_Y_1^3 + 2.5 * delta_Pre_Y_1^2 - 4 * delta_Pre_Y_1 + 2;
        W_delta_Pre_Y_2 = 1.5 * delta_Pre_Y_2^3 - 2.5 * delta_Pre_Y_2^2 + 1;
        W_delta_Pos_Y_2 = 1.5 * delta_Pos_Y_2^3 - 2.5 * delta_Pos_Y_2^2 + 1;
        W_delta_Pos_Y_1 = -0.5 * delta_Pos_Y_1^3 + 2.5 * delta_Pos_Y_1^2 - 4 * delta_Pos_Y_1 + 2;


        Pre_Index_X_in_Extend_1 = Index_X_Ori + 1;
        Pre_Index_X_in_Extend_2 = Pre_Index_X_in_Extend_1 + 1;
        Pos_Index_X_in_Extend_2 = Pre_Index_X_in_Extend_2 + 1;
        Pos_Index_X_in_Extend_1 = Pos_Index_X_in_Extend_2 + 1;
        Pre_Index_Y_in_Extend_1 = Index_Y_Ori + 1;
        Pre_Index_Y_in_Extend_2 = Pre_Index_Y_in_Extend_1 + 1;
        Pos_Index_Y_in_Extend_2 = Pre_Index_Y_in_Extend_2 + 1;
        Pos_Index_Y_in_Extend_1 = Pos_Index_Y_in_Extend_2 + 1;



        Value_Target = W_delta_Pre_X_1 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_1);

        Bicubic_Interp_imageData(i, j) = Value_Target;
    end
end
figure(5);
imshow(uint8(Bicubic_Interp_imageData));
title('双三次插值结果', 'fontsize', 17);


% 双三次B样条插值
Bicubic_BLine_Interp_imageData = zeros(Interp_rowCount, Interp_colCount);
for i = 1 : Interp_rowCount
    for j = 1 : Interp_colCount
        Index_X_Target = j;
        Index_Y_Target = i;

        First_Ori_Index_in_Target = (Ratio + 1) / 2;
        Index_X_Ori = floor((Index_X_Target - First_Ori_Index_in_Target) / Ratio + 1);
        Index_Y_Ori = floor((Index_Y_Target - First_Ori_Index_in_Target) / Ratio + 1);

        % 目标点左上角网格点的坐标
        Index_X_Ori_in_Target = First_Ori_Index_in_Target + (Index_X_Ori - 1) * Ratio;
        Index_Y_Ori_in_Target = First_Ori_Index_in_Target + (Index_Y_Ori - 1) * Ratio;

        delta_Pre_X_1 = (Index_X_Target - (Index_X_Ori_in_Target - Ratio)) / Ratio;
        delta_Pre_X_2 = (Index_X_Target - Index_X_Ori_in_Target) / Ratio;
        delta_Pos_X_2 = 1 - delta_Pre_X_2;
        delta_Pos_X_1 = delta_Pos_X_2 + 1;
        delta_Pre_Y_1 = (Index_Y_Target - (Index_Y_Ori_in_Target - Ratio)) / Ratio;
        delta_Pre_Y_2 = (Index_Y_Target - Index_Y_Ori_in_Target) / Ratio;
        delta_Pos_Y_2 = 1 - delta_Pre_Y_2;
        delta_Pos_Y_1 = delta_Pos_Y_2 + 1;


        % 双三次B样条插值————权重函数
        W_delta_Pre_X_1 = -(1 / 6) * delta_Pre_X_1^3 + delta_Pre_X_1^2 - 2 * delta_Pre_X_1 + (4 / 3);
        W_delta_Pre_X_2 = 0.5 * delta_Pre_X_2^3 - delta_Pre_X_2^2 + (2 / 3);
        W_delta_Pos_X_2 = 0.5 * delta_Pos_X_2^3 - delta_Pos_X_2^2 + (2 / 3);
        W_delta_Pos_X_1 = -(1 / 6) * delta_Pos_X_1^3 + delta_Pos_X_1^2 - 2 * delta_Pos_X_1 + (4 / 3);
        W_delta_Pre_Y_1 = -(1 / 6) * delta_Pre_Y_1^3 + delta_Pre_Y_1^2 - 2 * delta_Pre_Y_1 + (4 / 3);
        W_delta_Pre_Y_2 = 0.5 * delta_Pre_Y_2^3 - delta_Pre_Y_2^2 + (2 / 3);
        W_delta_Pos_Y_2 = 0.5 * delta_Pos_Y_2^3 - delta_Pos_Y_2^2 + (2 / 3);
        W_delta_Pos_Y_1 = -(1 / 6) * delta_Pos_Y_1^3 + delta_Pos_Y_1^2 - 2 * delta_Pos_Y_1 + (4 / 3);


        Pre_Index_X_in_Extend_1 = Index_X_Ori + 1;
        Pre_Index_X_in_Extend_2 = Pre_Index_X_in_Extend_1 + 1;
        Pos_Index_X_in_Extend_2 = Pre_Index_X_in_Extend_2 + 1;
        Pos_Index_X_in_Extend_1 = Pos_Index_X_in_Extend_2 + 1;
        Pre_Index_Y_in_Extend_1 = Index_Y_Ori + 1;
        Pre_Index_Y_in_Extend_2 = Pre_Index_Y_in_Extend_1 + 1;
        Pos_Index_Y_in_Extend_2 = Pre_Index_Y_in_Extend_2 + 1;
        Pos_Index_Y_in_Extend_1 = Pos_Index_Y_in_Extend_2 + 1;



        Value_Target = W_delta_Pre_X_1 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_1);

        Bicubic_BLine_Interp_imageData(i, j) = Value_Target;
    end
end
figure(6);
imshow(uint8(Bicubic_BLine_Interp_imageData));
title('双三次B样条插值结果', 'fontsize', 17);


% 双自适应有理接触式插值
BiAdpat_sculatory_rational_Interp_imageData = zeros(Interp_rowCount, Interp_colCount);
for i = 1 : Interp_rowCount
    for j = 1 : Interp_colCount
        Index_X_Target = j;
        Index_Y_Target = i;

        First_Ori_Index_in_Target = (Ratio + 1) / 2;
        Index_X_Ori = floor((Index_X_Target - First_Ori_Index_in_Target) / Ratio + 1);
        Index_Y_Ori = floor((Index_Y_Target - First_Ori_Index_in_Target) / Ratio + 1);

        % 目标点左上角网格点的坐标
        Index_X_Ori_in_Target = First_Ori_Index_in_Target + (Index_X_Ori - 1) * Ratio;
        Index_Y_Ori_in_Target = First_Ori_Index_in_Target + (Index_Y_Ori - 1) * Ratio;

        delta_Pre_X_1 = (Index_X_Target - (Index_X_Ori_in_Target - Ratio)) / Ratio;
        delta_Pre_X_2 = (Index_X_Target - Index_X_Ori_in_Target) / Ratio;
        delta_Pos_X_2 = 1 - delta_Pre_X_2;
        delta_Pos_X_1 = delta_Pos_X_2 + 1;
        delta_Pre_Y_1 = (Index_Y_Target - (Index_Y_Ori_in_Target - Ratio)) / Ratio;
        delta_Pre_Y_2 = (Index_Y_Target - Index_Y_Ori_in_Target) / Ratio;
        delta_Pos_Y_2 = 1 - delta_Pre_Y_2;
        delta_Pos_Y_1 = delta_Pos_Y_2 + 1;


        % 双自适应有理接触式插值————权重函数
        W_delta_Pre_X_1 = (0.1953 * delta_Pre_X_1^2 - 0.5858 * delta_Pre_X_1 + 0.3905) / (delta_Pre_X_1^2 - 2.4402 * delta_Pre_X_1 + 1.7676);
        W_delta_Pre_X_2 = (-0.168 * delta_Pre_X_2^2 - 0.9129 * delta_Pre_X_2 + 1.0808) / (delta_Pre_X_2^2 - 0.8319 * delta_Pre_X_2 + 1.0808);
        W_delta_Pos_X_2 = (-0.168 * delta_Pos_X_2^2 - 0.9129 * delta_Pos_X_2 + 1.0808) / (delta_Pos_X_2^2 - 0.8319 * delta_Pos_X_2 + 1.0808);
        W_delta_Pos_X_1 = (0.1953 * delta_Pos_X_1^2 - 0.5858 * delta_Pos_X_1 + 0.3905) / (delta_Pos_X_1^2 - 2.4402 * delta_Pos_X_1 + 1.7676);
        W_delta_Pre_Y_1 = (0.1953 * delta_Pre_Y_1^2 - 0.5858 * delta_Pre_Y_1 + 0.3905) / (delta_Pre_Y_1^2 - 2.4402 * delta_Pre_Y_1 + 1.7676);
        W_delta_Pre_Y_2 = (-0.168 * delta_Pre_Y_2^2 - 0.9129 * delta_Pre_Y_2 + 1.0808) / (delta_Pre_Y_2^2 - 0.8319 * delta_Pre_Y_2 + 1.0808);
        W_delta_Pos_Y_2 = (-0.168 * delta_Pos_Y_2^2 - 0.9129 * delta_Pos_Y_2 + 1.0808) / (delta_Pos_Y_2^2 - 0.8319 * delta_Pos_Y_2 + 1.0808);
        W_delta_Pos_Y_1 = (0.1953 * delta_Pos_Y_1^2 - 0.5858 * delta_Pos_Y_1 + 0.3905) / (delta_Pos_Y_1^2 - 2.4402 * delta_Pos_Y_1 + 1.7676);


        Pre_Index_X_in_Extend_1 = Index_X_Ori + 1;
        Pre_Index_X_in_Extend_2 = Pre_Index_X_in_Extend_1 + 1;
        Pos_Index_X_in_Extend_2 = Pre_Index_X_in_Extend_2 + 1;
        Pos_Index_X_in_Extend_1 = Pos_Index_X_in_Extend_2 + 1;
        Pre_Index_Y_in_Extend_1 = Index_Y_Ori + 1;
        Pre_Index_Y_in_Extend_2 = Pre_Index_Y_in_Extend_1 + 1;
        Pos_Index_Y_in_Extend_2 = Pre_Index_Y_in_Extend_2 + 1;
        Pos_Index_Y_in_Extend_1 = Pos_Index_Y_in_Extend_2 + 1;



        Value_Target = W_delta_Pre_X_1 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pre_Y_1 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pre_Y_2 * Extend_Bi_imageData(Pre_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pos_Y_2 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_2, Pos_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_1 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_1) +...
                       W_delta_Pre_X_2 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pre_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_2 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_2) +...
                       W_delta_Pos_X_1 * W_delta_Pos_Y_1 * Extend_Bi_imageData(Pos_Index_Y_in_Extend_1, Pos_Index_X_in_Extend_1);

        BiAdpat_sculatory_rational_Interp_imageData(i, j) = Value_Target;
    end
end
figure(7);
imshow(uint8(BiAdpat_sculatory_rational_Interp_imageData));
title('双自适应有理接触式插值结果', 'fontsize', 17);

附录

这里将介绍自适应接触式有理插值方法。

       自适应接触式有理插值本质上是使用 Thiele 型连分式插值方法去逼近Sinc函数：

       上图中的 Rn(x) 即为连分式插值函数，插值的目标即是在 (-2, 2) 区间内逼近理想的插值权重函数Sinc，同时做一些调整。上述连分式插值函数形式有些类似牛顿插值。

       权重函数具有对称性，逼近过程分为两步：1. 在 [0, 1] 区间内逼近Sinc函数；2. 在 (1, 2] 区间内进行自适应调整。

      在上述考量之下，所述的自适应接触式有理插值权重函数表达式如下：

       I(X)=\begin{cases} & \frac{-0.168|X|^2-0.9129|X|+1.0808}{|X|^2-0.8319|X|+1.0808} \quad\quad |X|\leqslant 1 \\ & \frac{a1|X|^2+b1|X|+c1}{|X|^2+b2|X|+c2} \quad\quad\qquad\qquad \ 1< |X|\leqslant 2 \\ & 0 \qquad\qquad\qquad\qquad\qquad\quad \ \ 2< |X| \end{cases}

       上式中 (1, 2] 区间下的常数项 a1，b1，c1，c2 与插值点与最邻近网格点（插值基）的距离 d 相关，即权重函数与插值点的位置相关，因此称之为“自适应”。前述的“自适应接触有理插值方法的权值函数”为 d = 0.25 时的表达式。

       理论上，插值过程不用完全精确，不需要针对每个 d 都计算一次插值常数项。下面给出一些 d 下的常数项值，可供直接查表使用：

da1b1c1b2c2
0.10.3428-1.02850.6856-2.34381.8931
0.20.2494-0.74820.4988-2.39281.7957
0.250.1952-0.58570.3905-2.44031.7677
0.30.1393-0.41780.2786-2.50851.7676
0.40.0410-0.12310.0820-2.71641.8997

       以上参数经过实际测试，发现效果很难及预期。推测该方法存在缺陷，当使用自适应接触有理插值方法时，建议仅使用 d = 0.25 下的参数。

写这些主要是阅读文献后进行本地复现的一些所思所感，如有错误请不吝赐教。

下面是参考资料：

https://www.sciencedirect.com/science/article/pii/S0377042705004711（如无法跳转请直接复制至谷歌浏览器的搜索框中）

第七章 一元连分式插值和逼近 - 知乎 (zhihu.com)

sinc插值原理及其实现-CSDN博客

双三次插值法 - wancy - 博客园 (cnblogs.com)

乌雷尼奥
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值