一维插值

拉格朗日插值法:
可以用于少样本点的情况,一定可以返回较好的插值函数。当样本点较多时,函数复杂度急剧上升。
样条插值法:
低阶多项式进行拟合,误差比拉格朗日稍大,但是减轻了龙格现象。
线性插值与样条插值


#coding=<utf-8>
#线性差值问题,根据已知坐标点拟合函数
#B-spline插值问题,根据B样条拟合函数
import numpy as np
import pylab as pl
from scipy import interpolate
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
#生成10个x等份点,用来拟合插值函数
x = np.linspace(0, 2*np.pi+np.pi/4, 10)
#根据x生成y点,用来拟合插值函数
y = np.sin(x)
#生成100个x点,用来画图
x_new = np.linspace(0, 2*np.pi+np.pi/4, 100)
#定义线性差值函数,将一维变量y插入x中
f_linear = interpolate.interp1d(x, y)
#形成样条关系式
tck = interpolate.splrep(x, y)
#将样条关系式应用于插值函数,并将x_new代入的到y_new
y_bspline = interpolate.splev(x_new, tck)
#可视化
plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')
plt.plot(x, y, "o", label=u"原始数据")#o表示实心点
plt.plot(x_new, f_linear(x_new), label=u"线性插值")
plt.plot(x_new, y_bspline, label=u"B-spline插值")
pl.legend()
pl.show()
高阶样条插值
因为多项式次数的增加,会导致插值的跳跃,一般控制插值函数的阶数在5个以下,即无规律的插值点控制在10个以下。

对sin(x^5)进行插值拟合的结果,高阶插值函数龙格现象明显变大。


#高阶样条插值
#创建数据点集
import numpy as np
import pylab as pl
from scipy import interpolate
from scipy.sparse.construct import rand, random
x = np.linspace(0, 10, 10)
y = np.sin(x**5)
#绘制数据点集
pl.figure(figsize=(12,9))#设置窗口大小
pl.plot(x, y, 'ro')#设置原始坐标点
xnew = np.linspace(0, 10, 101)
#根据kind创建interp1d对象f、计算插值结果
'''
nearest:中间拐角的阶梯状,零阶
zero:后一个点拐角的阶梯状,零阶
linear:一次多项式的连接,一阶
quadratic:二次多项式的连接,二阶
数字:直接表示阶数,最高位7
'''
for kind in ['nearest', 'zero', 'linear', 'quadratic',5]:
#设置插值函数
f = interpolate.interp1d(x, y, kind = kind)
#计算y
ynew = f(xnew)
#画出图像
pl.plot(xnew, ynew, label = str(kind))
pl.xticks(fontsize=20)#设置坐标轴样式
pl.yticks(fontsize=20)
pl.legend(loc='lower right')#标识出现在右下角
pl.show()
二维插值
二维插值的二维图

代码:
import numpy as np #矩阵类型
from scipy import interpolate #计算,拟合
import pylab as pl #画图
import matplotlib as mpl #画图
#生成插值点的函数
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2+y**2))
#X-Y轴分为15*15的网格,[起点,终点,格数j]
y, x = np.mgrid[-1:1:15j, -1:1:15j]
#计算每个网格点上函数值z
fvals = func(x, y)
#三次样条二维插值。得到插值函数
newfunc = interpolate.interp2d(x, y,fvals, kind='cubic')
#计算100*100网格上插值
xnew = np.linspace(-1,1,100)
ynew = np.linspace(-1,1,100)
fnew = newfunc(xnew, ynew)
#可视化
#让imshow的参数interpolation设置为’nearest’方便比较插值处理
#原始点
#1行两列,1号区域
pl.subplot(1,2,1)
#extent: x,y的范围 cmap:色谱 origin:坐标原点位置
im1 = pl.imshow(fvals, extent=[-1,1,-1,1],cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im1)
#插值
#一行两列,二号区域
pl.subplot(122)
im2 = pl.imshow(fnew, extent=[-1,1,-1,1], cmap=mpl.cm.hot, interpolation='nearest', origin="lower")
pl.colorbar(im2)
pl.show()

二维插值的三维图

#二维插值的三维图
import numpy as np
from scipy import interpolate
import matplotlib.cm as cm
import matplotlib.pyplot as plt
def func(x, y):
return (x+y)*np.exp(-5.0*(x**2+y**2))
#X-Y轴分为20*20的网格
x = np.linspace(-1,1,20)
y = np.linspace(-1,1,20)
x, y = np.meshgrid(x, y)
fvals = func(x, y)
#画分图1
#设置图像大小。(长,宽)
fig = plt.figure(figsize=(10, 7))
#建立分图句柄
ax = plt.subplot(1, 2, 1, projection = '3d')
#曲面绘制
#rstride:行宽 cstride:列宽 cmap:渐变 linewidth:线宽 antialiased:抗齿距
surf = ax.plot_surface(x, y, fvals, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
#设置坐标轴名称
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
plt.colorbar(surf, shrink=0.5, aspect=5)#添加颜色条标注
#二维插值
#生成三阶插值函数
newfunc = interpolate.interp2d(x, y, fvals, kind='cubic')
#计算100*100网格上插值
xnew = np.linspace(-1,1,100)
ynew = np.linspace(-1,1,100)
fnew = newfunc(xnew, ynew)
xnew, ynew = np.meshgrid(xnew, ynew)
#画分图2
ax2 = plt.subplot(1, 2, 2, projection = '3d')
surf2 = ax2.plot_surface(xnew, ynew, fnew, rstride=2, cstride=2, cmap=cm.coolwarm,linewidth=0.5, antialiased=True)
ax2.set_xlabel('xnew')
ax2.set_ylabel('ynew')
ax2.set_zlabel('fnew(x,y)')
plt.colorbar(surf2, shrink=0.5, aspect=5)#标注
plt.show()
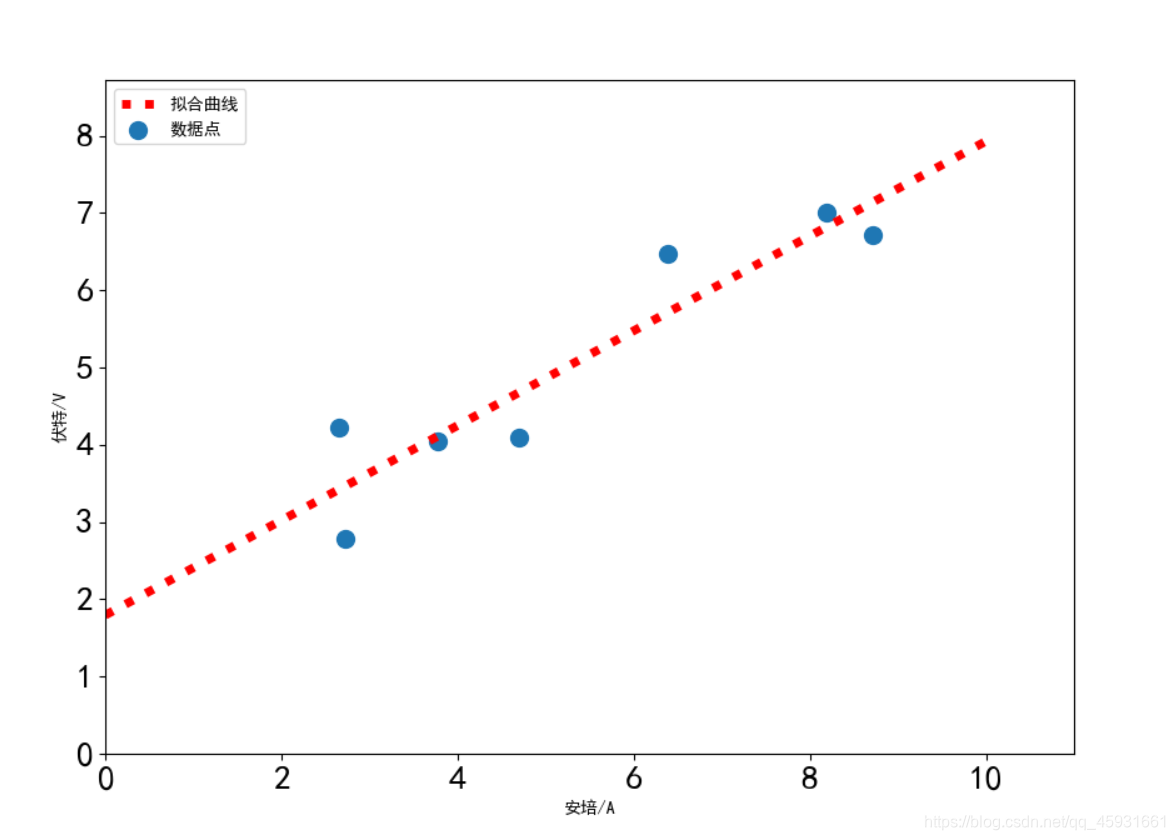
最小二乘拟合


#最小二乘拟合
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import leastsq
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
X=np.array([8.19, 2.72, 6.39, 8.71, 4.7, 2.66, 3.78])
Y=np.array([7.01, 2.78, 6.47, 6.71, 4.1, 4.23, 4.05])
#计算以p为参数的直线与原始数据之间误差
def f(p):
k, b = p
return(Y-(k*X+b))
#leastsq使得f的输出数组的平方和最小,参数初始值为[1,0]
r = leastsq(f, [1,0])
k, b = r[0]
#设置画布大小
plt.figure(figsize=(10,7))
#绘制散点图像
plt.scatter(X, Y, s=100, alpha=1.0, marker='o',label=u'数据点')
x=np.linspace(0,10,1000)
y=k*x+b
#获取坐标句柄
ax = plt.gca()
#绘图
#color:颜色 linewidth:线宽 linestyle: markersize: label=曲线的名称
plt.plot(x, y, color='r',linewidth=5, linestyle=":",markersize=20, label=u'拟合曲线')
#设置图例的位置
plt.legend(loc=0, numpoints=1)
leg = plt.gca().get_legend()
ltext = leg.get_texts()
#设置图例的字体
plt.setp(ltext, fontsize='xx-large')
plt.xlabel(u'安培/A')
plt.ylabel(u'伏特/V')
#设置最大值
plt.xlim(0, x.max() * 1.1)
plt.ylim(0, y.max() * 1.1)
#刻度的字体
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
#设置图例位置
plt.legend(loc='upper left')
plt.show()
























 628
628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








