卷积神经网络(CNN)详细介绍及Python代码实战

1、为何要提出CNN？

一张图片，在数学的世界里，是由一个个像素点组成的；而一个像素点，又是由RGB三元色按一定比例混合而成的。所以，一张图片可以由R、G、B三个数值矩阵所表示。如图1.1所示(由于未找到合适的彩色图像，这里用灰度图示例，灰度图由单一数值矩阵构成，而彩色图则包含三个矩阵)：

图 1.1
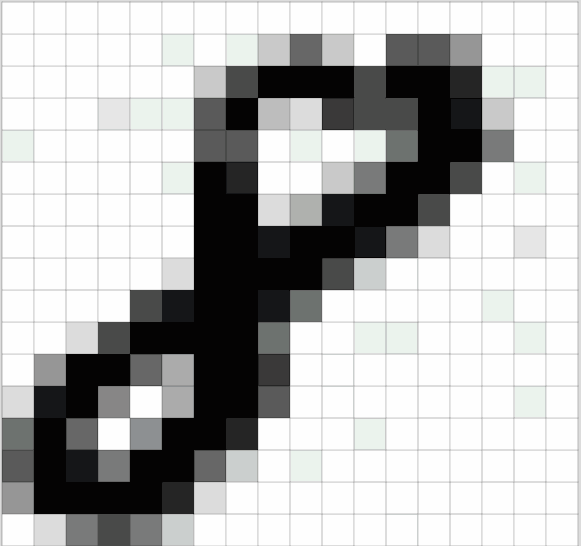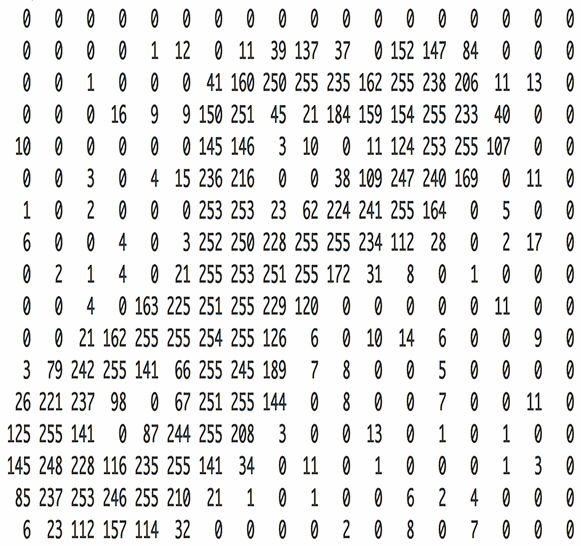
图片来源于博主 IronmanJay

在传统神经网络中，我们需要输入数据的特征，而这个特征只能是一维的；但是对于图片，它的特征是一个个的像素点，这些像素点被储存在矩阵中，以二维的形式存在，显然是无法输入到传统神经网络中去的。在卷积出现之前，我们的做法是将二维特征拉伸成一维，再输入神经网络。虽然解决了输入端的问题，但却导致了信息损失：在二维像素矩阵中，每个像素点与其周围的像素点存在着空间关系，一旦展平成一维，这些宝贵的位置信息便丢失了，从而影响了模型的预测效果。

此外，图片由成千上万的像素点组成，如果采用全连接层，将产生巨大的参数数量，这样的训练成本往往是不可承受的。

1998年，Yann LeCun等人发表论文《Gradient-based learning applied to document recognition》正式提出了CNN的概念，很好地解决了图片特征提取的问题。下面，我们就来详细介绍一下CNN的原理。

2、如何实现CNN？

2.1 CNN与传统神经网络的结构差异

传统神经网络由输入层、隐藏层（位于输入层和输出层之间）和输出层组成，每层由一字排开的全连接的神经元构成，如图2.1所示：

图 2.1

显然，这种结构无法直接处理二维特征矩阵输入。因此，在CNN中，我们对输入层和隐藏层的结构进行了调整（输出层保持不变，原因后续解释），如图2.2所示：

图 2.2

我们可以看到，CNN的输入层接受二维数值矩阵，而隐藏层由传统的全连接层变为了卷积层和池化层；最后通过全连接层进行输出。输入端的改变是为了适应二维矩阵输入；输出端保持不变是因为无论哪种神经网络，我们的最终任务是相同的，因此输出层的结构也应保持一致。现在，我们重点关注隐藏层的变化。隐藏层的目标是提取特征和融合信息，供输出层做出最佳判断。那么，池化层和卷积层是如何实现这一目标的呢？接下来的内容将对此进行详细介绍。

2.2 卷积层

卷积层作为CNN隐藏层的核心结构，其目的是提取并浓缩图片的二维矩阵信息。在传统神经网络中，一个隐藏层包含n个神经元；而在CNN中，一个卷积层包含n个卷积核。卷积核本身也是一个二维矩阵，尺寸小于输入矩阵，通过在输入矩阵上滑动并执行计算，实现信息提取。具体的运算步骤如图2.3所示：

图 2.3

图2.4是一个具体的例子：

图 2.4

图2.5是卷积核滑动的动图演示：

图 2.5
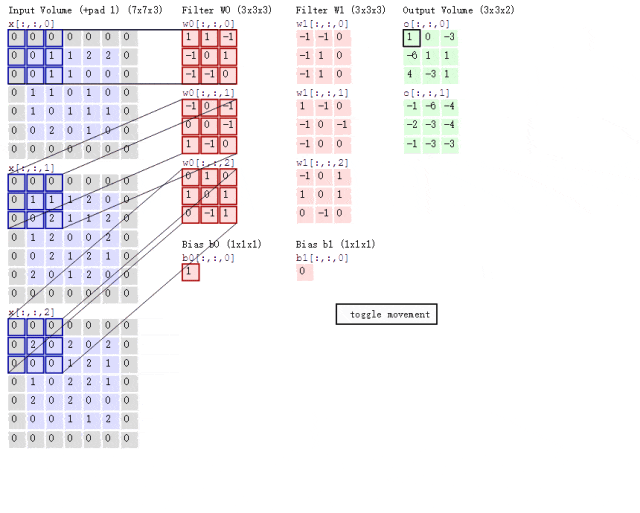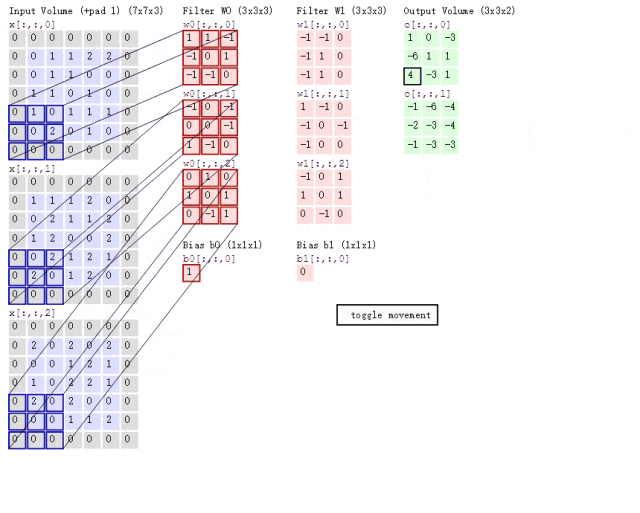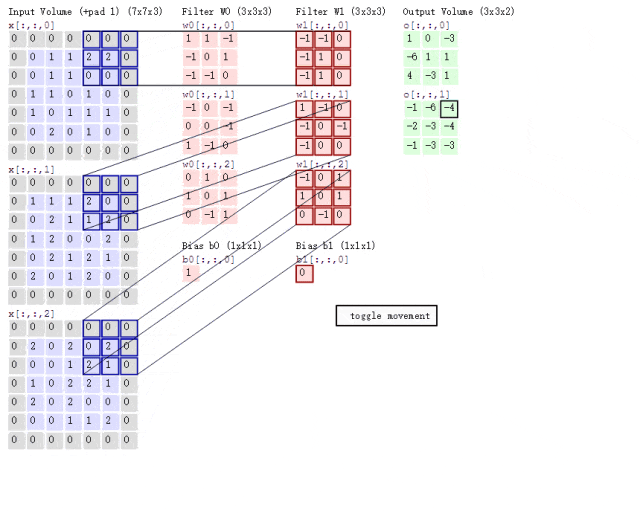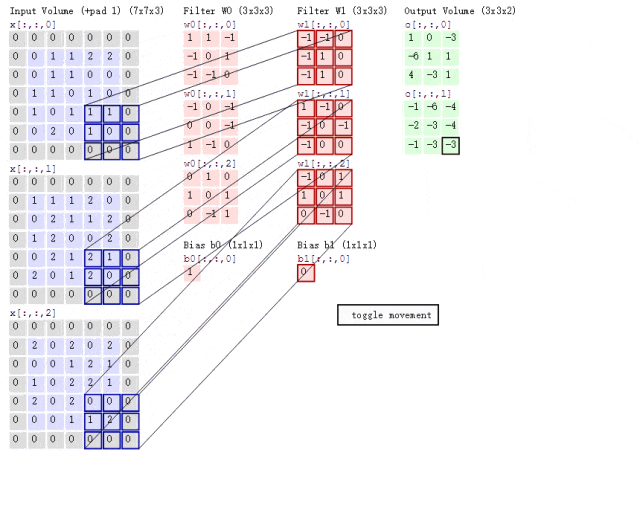
图片来自于博主 IronmanJay

2.2.1 易混淆点：卷积核的层数与卷积核的数量

为了解释清楚这个概念，我们必须引入通道的概念：

• 通道(channel)：
  • 图像通道：输入层数据的通道数。例如，在彩色图像中，通道指的是颜色的组成部分，通常是红色（Red）、绿色（Green）、蓝色（Blue）三种颜色，分别对应三个独立的通道。每个通道包含了图像在该颜色维度上的强度信息。
  • 特征通道：除了输入层的通道外，网络的每一层卷积层都可以生成多个特征通道，每个通道提取输入数据的不同特征，例如边缘、纹理、形状等。特征通道的数量由该层的卷积核数量决定，例如，某个卷积层有16个卷积核，则该层的输出将具有16个通道

卷积核的数量可以根据需要设定，但每个卷积核的层数取决于其所作用数据的通道数。第一个卷积层的卷积核数等于图像通道数，后面的卷积层中的卷积核数等于特征通道数。例如，在图2.5中，输入数据有3个通道，因此每个卷积核也必须有3层。经过卷积层处理后，传入下一个卷积层的数据通道数将等于上一层设定的卷积核数量。每个卷积核产生一个特征通道。

2.3 池化层

继卷积层提取特征之后，池化层接棒进一步处理这些特征信息。池化层的主要目的是降低数据的空间维度，从而减少计算量，并使特征检测更加鲁棒。这一过程同时保留了重要的特征信息，确保了模型对输入数据的泛化能力。

池化操作通常在卷积层输出的特征图上进行。想象一下，特征图是一块由多个小网格组成的大画布，每个小网格包含了卷积层提取的特定特征。池化层的作用就是将这些小网格中的数据进行聚合，以一种统计方式（如取最大值或平均值）来代表每个区域的主要信息。

2.3.1 池化层的工作原理

1. 选择池化窗口：首先，我们选定一个池化窗口（例如2x2大小），这个窗口将在特征图上滑动。
2. 应用池化函数：接着，我们对这个窗口内的数据应用池化函数。最常见的池化函数有两种：
   • 最大池化（Max Pooling）：选择窗口内的最大值，这个值代表了该区域最显著的特征。
   • 平均池化（Average Pooling）：计算窗口内所有值的平均数，以获取区域特征的平均表示。
3. 滑动窗口：池化窗口在特征图上按照设定的步长滑动，并重复应用池化函数，直到覆盖整个特征图。

具体过程如图2.5所示：

以最大池化为例

2.3.2 池化层的优势

• 降维：池化层显著减少了数据的空间尺寸，从而减少了后续层的参数数量和计算量。
• 不变性：通过池化操作，模型对输入数据的平移、缩放和旋转等变换具有更好的不变性。
• 特征强化：池化层通过聚合操作强化了特征的表达，有助于保留最重要的信息。

3. 基于Pytorch的CNN实战代码

import torch
import torch.nn.functional as F
from torch.utils.data import Dataset, Subset
from torch import nn
from torch import optim
from sklearn.metrics import accuracy_score
from torchvision import datasets,transforms

#归一化
transform = transforms.Compose([
    transforms.ToTensor(), # 将像素值转换到[0, 1]
    transforms.Normalize((0.5,), (0.5,))  # 映射到-1到1的范围
])

# 下载训练集和测试集
trainset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
testset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)

# 原数据太多，采用抽样数据
# train
sampled_train_indices = torch.randperm(len(trainset))[:7000]  # 抽样索引
sampled_trainset = Subset(trainset, sampled_train_indices)  # 使用Subset创建抽样的数据集
# test
sampled_test_indices = torch.randperm(len(testset))[:3000]
sampled_testset = Subset(testset, sampled_test_indices)

# 创建DataLoader来迭代数据集
trainloader = torch.utils.data.DataLoader(sampled_trainset, batch_size=128, shuffle=True)
testloader = torch.utils.data.DataLoader(sampled_testset, batch_size=3000, shuffle=False)

class cnn(nn.Module):
    def __init__(self, input_channel):
        super().__init__()
        self.input_channel = input_channel
        # nn.Conv2d(in_channels(输入通道数),out_channels(输出通道数),kernel_size(卷积核大小),stride(卷积核滑动步长))
        self.conv1 = nn.Conv2d(in_channels=self.input_channel,out_channels=64,kernel_size=(4,4),stride=1)
        # nn.MaxPool2d(kernel_size(池化核大小),stride(池化核滑动步长))
        self.pool1 = nn.MaxPool2d(kernel_size=(2,2),stride=1)

        self.conv2 = nn.Conv2d(in_channels=64,out_channels=32,kernel_size=(4,4),stride=1)
        self.pool2 = nn.MaxPool2d(kernel_size=(2,2),stride=1)

        self.relu = nn.ReLU()
        self.fc = nn.Linear(32*20*20,10)
        self.softmax = nn.Softmax(dim=1)

    def forward(self,x):
        # 一层卷积
        x = self.conv1(x)
        x = self.pool1(x)
        x = self.relu(x)
        # 二层卷积
        x = self.conv2(x)
        x = self.pool2(x)
        x = self.relu(x)
        # 全连接层
        # x拉平
        x = x.view(x.shape[0],-1)
        x = self.fc(x)
        x = self.softmax(x)
        return x


def main(epoches):
    # 如果是彩色图片input_channel=3
    model = cnn(input_channel=1)
    # 定义优化器
    optimizer = optim.Adam(params=model.parameters(), lr=0.001)
    # 定义损失函数
    criterion = nn.MSELoss()
    # 开始训练
    model.train()
    # epoch级遍历
    for epoch in range(epoches):
        # 储存一个epoch的损失
        Loss = 0
        # batch级遍历
        for batch_x, batch_y in trainloader:
            # 采用one-hot编码
            batch_y = F.one_hot(batch_y,num_classes=10)
            # cnn前向传播得到输出
            outputs = model.forward(batch_x)
            # 计算损失
            loss = criterion(batch_y.to(torch.float), outputs)
            Loss += loss
            # 清空梯度
            optimizer.zero_grad()
            # 计算梯度
            loss.backward()
            # 用梯度更新参数
            optimizer.step()
        # 每个epoch完都打印损失值信息
        if epoch % 1 == 0:
            print('epoch:{}/{}, loss:{}'.format(epoch+1,epoches,Loss))

    # 开始预测
    model.eval()
    # 禁用梯度
    with torch.no_grad():
        for tx,ty in testloader:
            outputs = model.forward(x=tx)
            pre_y = torch.argmax(outputs,dim=1)
            acc =accuracy_score(pre_y,ty)
            return acc
acc = main(epoches=5)
print(acc)