1、唯一分解定理
2、阶乘质因子分解
3、欧几里得、扩展欧几里得
4、逆元
5、卡特兰数通项公式
一、唯一分解定理
任何一个大于1的整数n都可以分解成若干个素因数的连乘积,如果不计各个素因数的顺序,那么这种分解是唯一的。
即n=p1a1p2a2…pkak
(1)一个大于1的正整数N,如果他的标准分解式为N=P1a1P2a2…Pnan,那么它的正因数个数之和为
σ(N)=(1+a1)(1+a2)…(1+an)。
(2)它的全体正因数之和为
σ1(N)=(1+p1+p12+…+p1a1)(1+p2+p22+…+p2a2)…(1+pn+pn2+…+pnan)。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
using namespace std;
const int MAXN=100001;
int p[MAXN],c[MAXN];//p数组表示该因子,c数组表示在p中对应因子的次数
int n,sum;
int main()
{
while(scanf("%d",&n)!=EOF){
memset(c,0,sizeof(c));
sum=0;
int m=sqrt(n);
for(int i=2;i<=m;i++){
if(n%i==0){
p[++sum]=i;
while(n%i==0){
n/=i;
c[sum]++;
}
}
}
if(n>1){
p[++sum]=n;
c[sum]++;
}
for(int i=1;i<=sum;i++)
printf("%d %d\n",p[i],c[i]);
}
return 0;
}
二、阶乘质因子分解
贡献为2的:[n/2]+[n/22]+[n/23]+…
贡献为3的:[n/3]+[n/32]+[n/33]+…
贡献为5的:[n/5]+[n/52]+[n/53]+…
…
#include<iostream>
using namespace std;
const int MAXN=1e8+10;
int n,t,sum;
int prime[MAXN],visit[MAXN],cnt[MAXN];
//素数筛
int set(int n){
for(int i=2;i<=n;i++){
if(!visit[i]){
prime[++sum]=i;
}
for(int j=1;j<=sum&&i*prime[j]<=n;j++){
visit[i*prime[j]]=1;
if(!i%prime[j]){
break;
}
}
}
}
int main()
{
scanf("%d",&n);
set(n);
//质因子分解
for(int i=1;i<=sum;i++){
t=n;
while(t)
{
cnt[i]+=t/prime[i];
t/=prime[i];
}
}
for(int i=1;i<=sum;i++)
cout<<prime[i]<<" "<<cnt[i]<<endl;
cout<<endl;
return 0;
}
三、欧几里得+扩展欧几里得
(1)欧几里得算法
欧几里德有个定理: gcd(a, b) = gcd(b , a%b) ,这样我们就可以在几乎是 log 的时间复杂度里求解出来 a 和 b 的最大公约数了,这就是欧几里德算法, C++ 语言描述如下:
//辗转相除求gcd
int gcd(int a,int b)
{
if(b==0) return a;
else return gcd(b,a%b);
}
(2)扩展欧几里得算法
现在我们知道了 a 和 b 的最大公约数是 gcd ,那我们能够找到这样的 x 和 y ,使得: ax + by = gcd 这是一个不定方程,有多解是一定的,但是只要我们找到一组特殊的解 x0 和 y0 那么,我们就可以用 x0 和 y0 表示出整个不定方程的通解:
ax+by=c①
ax0+by0=c②
①-②联立解得a(x-x0)+b(y-y0)=0
即a(x-x0)=b(y0-y)
若a、b互质,那么x-x0一定含因子b,y0-y必含因子a
即x-x0=kb,y0-y=ka(k∈Z)
所以通解为x=x0+bk,y=y0-ak
若c=gcd(a,b),求特解x 和 y 只需要在欧几里德算法的基础上加点改动,欧几里德算法停止的状态是: a= gcd , b = 0 。这时候,只要 a = gcd 的系数是 1 ,那么只要 b 的系数是 0,我们就会有: a1 + b0 = gcd
由欧几里得定理gcd(a,b)=gcd(b,a%b)
ax1+by1=bx2+(a%b)y2
ax1+by1=bx2+[a-(a/b)b]y2
ax1+by1=bx2+ay2-b(a/b)y2
ax1+by1=ay2+b[x2-(a/b)y2]
所以x1=y2,y1=x2-(a/b)y2,用递归求解,边界条件gcd(a,0)
int exgcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;
b=0;
return a;
}
int ans=exgcd(b,a%b,x,y);
int tmp=x;
x=y;
y=tmp-a/b*y;
return ans;
}
四、逆元
条件:若a, p 互质,a有关于p的逆元。
a的逆元表示为inv(a),ainv(a) ≡ 1 mod p
求法①费马小定理
a^(p-1) ≡1 (mod p)
两边同除以a
a^(p-2) ≡1/a (mod p)
即inv(a)≡a^(p-2) (mod p)
求法②欧几里得算法
ax + b*y = 1
如果a,b互质,有解x1 y1
x1就是a关于b的逆元
y1就是b关于a的逆元
证明:
两边同时对b取模
a*x % b= 1 %b
即a*x ≡ 1 (mod b)
五、卡特兰数通项公式
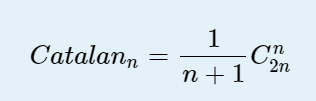




















 1033
1033











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








