【完美复现】基于多智能体系统一致性算法的电力系统分布式经济调度策略（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于多智能体系统一致性算法的电力系统分布式经济调度策略研究

一、多智能体系统一致性算法的基本原理

二、电力系统分布式经济调度的核心目标与约束

三、现有应用案例

四、理论框架与研究现状

五、性能评估指标

六、主要技术挑战

七、未来研究方向

结论

📚2 运行结果

2.1 场景1

2.2 场景2

2.3 场景3

2.4 场景4

🎉3 参考文献

🌈4 Matlab代码及数据

---

💥1 概述

文献来源：

基于多智能体系统一致性算法的电力系统分布式经济调度策略研究

 经济调度是电力系统运行中的一个基本问题，它是指发电机和柔性负荷在满足一系列运行约束的

条件下，使整个电力系统运行的社会福利最大化的优化问题。 传统上采用集中优化技术来解决经济调度问题，其中包括经典优化方法［1］ 和现代人工智能方法［2-4］ 。

然而，当采用集中优化方法时，系统需要调度中心发布指令调度整个系统中所有的发电机和柔性负

荷，调度中心需要与每一个调度对象进行信息交互［5］ 。并 且，柔性负荷的广泛渗透以及电力元件需要的“即插即用”技术将会使电力网和通信网拓扑结构多变［6］ ，导致集中优化方法需要较高的通信拓扑建设成本。 因此，需要适应性更强的优化算法，在通信受限和不可靠甚至调度中心失效的情况下仍能 有效地运行［7］ 。 分布式优化为解决上述问题提供了新方法［8-9］ 。在分布式优化算法中，一个基本的问题就是需要所有的节点都能达到一致，即多智能体系统中的

一致性［10］ 。 此类一致性问题已经在很多领域都进行了研究，比如机器人系统［11］ 、无人机系统［12］ ，以及传感器网络系统［13］ 。

多智能体系统的一致性算法能够应用于电力系统并实现其分布式优化运行［8-9，14-15］ 。 电力系统是一系列可控电力设备（发电机和柔性负荷）的有机组合，这些可控电力设备通过通信网络实现信息交互［6］ 。将发电机和柔性负荷建模为智能体，进一步将电力系统建模为多智能体系统，发电机和柔性负荷（智能体）通过局部通信网络与其他智能体进行信息交互，

实现整个电力系统（多智能系统）的协调优化运行。文献［8］提出了一种“Leader-Follower”分布式一致性算 法；文 献［9］提 出 几 种 Leader 的 选 择 方 法；文 献

［14］提出了一种两层分布式一致性算法；文献［15］通过创新项来实现完全分布式最优化。 值得关注的是，柔性负荷在电力系统中的渗透越来越广泛，而上述文献都没有考虑经济调度中的柔性负荷。

本文介绍了一致性算法的基本概念，应用一致性算法，以发电机组的增量成本（IC）与柔性负荷的增量效益（IB）作为一致性变量，设计一致性算法实现计及柔性负荷的电力系统分布式经济调度，算例仿真与分析表明了本文提出的分布式经济调度策略能够实现柔性负荷“即插即用”，降低通信网投资，有效应对通信网拓扑结构多变的问题。

一、多智能体系统一致性算法的基本原理

多智能体系统一致性算法是实现分布式协调的核心工具，其核心目标是通过局部信息交互使所有智能体状态收敛至相同值。该算法的理论基础可追溯至1959年关于群体决策一致性的模型，而现代框架由Saber和Murray提出的连续时间线性一致性协议奠定基础，仅需邻居信息即可实现全局一致性。关键原理包括：

1. 单积分器模型：智能体状态更新采用加权平均邻居状态的动态方程，形式为：

   

   其中aijaij​为邻接权重，NiNi​为邻居集合。离散化后通过差分方程调整步长实现收敛。

2. 网络拓扑与代数图论：无向连通图拓扑下，拉普拉斯矩阵的代数连通度决定收敛速度。强连通有向图需满足生成树条件。

3. 稳定性分析：基于Lyapunov函数构造，如V=σiT(t)Pσi(t)，通过分析导数V˙V˙的期望值推导稳定性条件，例如要求增益参数满足：

   

   其中δ为最小特征值或调节系数。

4. 扩展模型：双积分器系统（如无人机编队）需考虑速度与位置同步，高阶系统（如三阶模型）涉及加速度协调。

二、电力系统分布式经济调度的核心目标与约束

目标：

1. 经济性：最小化总发电成本，典型模型为二次函数：

   

   其中Pi为发电机出力，ai,bi,ci为成本系数。

2. 环境性：减少碳排放，优先调度可再生能源。

3. 可靠性：保障供电连续性，如通过备用容量分配。

4. 电能质量：维持电压、频率在±10%和±0.5Hz范围内。

约束：

1. 功率平衡：∑Pi=∑Dj∑Pi​=∑Dj​，需动态匹配负荷需求。
2. 设备容量：Pi,min⁡≤Pi≤Pi,max⁡Pi，考虑爬坡率限制。

   

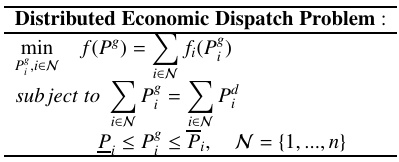
3. 网络安全：避免线路过载，满足N-1准则。
4. 通信拓扑：需保证连通性以支撑分布式算法收敛。

三、现有应用案例

1. MATLAB仿真平台：10机19负荷系统验证，通过增量成本（dFidPidPi​dFi​​）和柔性负荷增量效益的一致性调整实现优化，代码支持实时调试。
2. 交直流混合配电网：采用多智能体分层控制，将台区划分为子区块，通过Actor-Critic强化学习降低网络损耗10-15%，解决电压越限问题。
3. 微电网经济调度：
   • 改进领导-跟随算法，加入功率偏差消除项，使运行成本降低8%。
   • 有限时间一致性算法实现30秒内收敛，提升频率控制精度至±0.1Hz。
4. 储能系统协调：设计统一二次控制器，在IEEE 118节点系统中实现PCC点电压频率误差<0.5%，功率分配误差<3%。
5. 电动汽车集群调度：基于一致性算法的“即插即用”策略，在IEEE 39节点系统中支持20%渗透率下的动态接入。

四、理论框架与研究现状

1. 一致性变量设计：
   • 传统机组：增量成本λi=2aiPi+biλi​=2ai​Pi​+bi​。
   • 新能源机组：增量可用率（基于预测误差修正）。
   • 柔性负荷：增量效益μj=dUjdDjμj​=dDj​dUj​​。
2. 分布式优化架构：
   • 分层控制：三级结构（一次下垂控制、二次一致性补偿、三级经济优化）实现解耦。
   • 隐私保护：状态分解算法结合区块链技术，减少敏感数据暴露。
3. 通信机制创新：
   • 定向通信降低时延影响，推导时延上界为τmax⁡<π2ωmax⁡​。
   • FISCO BCOS平台结合rPBFT共识，提升拓扑动态适应性。
4. 算法扩展性：
   • 处理非凸成本函数：基于KKT条件动态修改功率约束，支持可转移负荷调度。
   • 多目标优化：整合发电成本、碳排放、储能损耗，权重系数可调。

五、性能评估指标

1. 经济性：总成本降低率（对比集中式基准）、边际成本一致性误差（<0.01$/MWh）。
2. 收敛性：收敛时间（如50次迭代内）、振荡幅度（标准差<2%）。
3. 鲁棒性：
   • 通信故障：随机丢包率<15%时仍收敛。
   • 拓扑变化：节点增减后恢复时间（<5s）。
4. 电能质量：电压偏差（<5%）、频率偏移（<0.2Hz）。
5. 计算效率：单次迭代时间（<10ms）、内存占用（<50MB）。

六、主要技术挑战

1. 复杂动态环境：
   • 高比例可再生能源波动导致功率预测误差（>20%），需融合概率性一致性算法。
   • 多时间尺度耦合：秒级频率调节与小时级经济调度的协调难题。
2. 通信瓶颈：
   • 时延敏感：时延>100ms可能导致发散，需硬件级时间同步（如PTP协议）。
   • 带宽限制：大规模系统通信负载随节点数呈O(n2)O(n2)增长，需稀疏拓扑优化。
3. 异构系统整合：
   • 控制模式差异：下垂控制、PQ控制、V/f控制间的接口标准化问题。
   • 多能源耦合：电-热-气耦合系统中跨介质一致性变量设计困难。
4. 安全与隐私：
   • 数据篡改风险：需结合轻量级加密（如国密SM4）。
   • 局部信息泄露：差分隐私注入噪声可能导致优化偏差（约3-5%）。
5. 非凸与非光滑问题：
   • 机组组合问题：启停成本导致目标函数不连续，需混合整数一致性算法。
   • 网损建模：动态网损补偿误差可能累积至5-8%。

七、未来研究方向

1. 跨学科融合：结合联邦学习实现预测-调度一体化，利用量子计算加速大规模优化。
2. 硬件在环测试：基于RT-LAB等平台验证微秒级实时性。
3. 标准体系构建：制定多智能体通信协议（如IEEE 2030.7）与一致性变量标准化。
4. 弹性增强设计：抗灾变一致性算法，支持极端事件下孤岛运行。

结论

多智能体一致性算法为电力系统分布式经济调度提供了理论基础与实用工具，其在经济性、可扩展性方面显著优于集中式方法。然而，动态环境适应性、通信可靠性及异构系统整合仍是亟待突破的瓶颈。未来需结合新一代信息技术与跨学科方法，推动该领域向更高智能化和鲁棒性方向发展。

📚2 运行结果

2.1 场景1

验证了该分布式调度算法与集中式调度算法一样，能收敛到最优解；

2.2 场景2

验证了该分布式调度策略对不同通信拓扑的适应性；

2.3 场景3

验证了该分布式调度策略能够有效应对电力元件功率约束发生作用的情形；

2.4 场景4

验证了该分布式调度策略能够使电力元件具备“即插即用”的能力。

部分代码：

 for i=1:1:10 %判断pg是否越限并赋值

   if (ll(t,i)-be(i))/(2*ga(i))>=pgmax(i)

     pgg(t+1,i)=pgmax(i);

   elseif (ll(t,i)-be(i))/(2*ga(i))<=pgmin(i)

     pgg(t+1,i)=pgmin(i);

   else

     pgg(t+1,i)=(ll(t,i)-be(i))/(2*ga(i));

   end

 end

  

 for j=1:1:19 %判断pd是否越限并赋值

   if (ll(t,j+10)-b(j))/(2*c(j))>=pdmax(j)

     pdd(t+1,j)=pdmax(j);

   elseif (ll(t,j+10)-b(j))/(2*c(j))<=pdmin(j)

     pdd(t+1,j)=pdmin(j);

   else

     pdd(t+1,j)=(ll(t,j+10)-b(j))/(2*c(j));

🎉3 参考文献

文章中一些内容引自网络，会注明出处或引用为参考文献，难免有未尽之处，如有不妥，请随时联系删除。

[1]谢俊,陈凯旋,岳东等.基于多智能体系统一致性算法的电力系统分布式经济调度策略[J].电力自动化设备,2016,36(02):112-117.DOI:10.16081/j.issn.1006-6047.2016.02.018.

🌈4 Matlab代码及数据