【Leetcode】790. Domino and Tromino Tiling

题目地址：

https://leetcode.com/problems/domino-and-tromino-tiling/description/

给定一个$2\times n$的矩阵，有两种类型的骨牌如下：

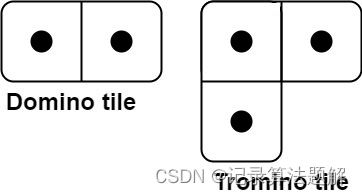
问要铺满矩阵，一共有多少不同的方案。答案模$10^9+7$后返回。

假设$f[k][x]$是已经铺到了第$k$列，并且第$k+1$列的状态为$x$的情况下的方案数。状态$x$是第$k$列的形状的二进制压缩，即$0$代表上下都空，$1$代表上空下不空，$2$代表上不空下空，$3$代表都不空。那么答案就是$f[n][0]$。考虑状态转移然后递推一遍即可。代码如下：

class Solution {
 public:
  int numTilings(int n) {
    const int MOD = 1e9 + 7;
    vector<vector<int>> f(n + 1, vector<int>(4));
    bool g[4][4] = {
      {1, 1, 1, 1},
      {0, 0, 1, 1},
      {0, 1, 0, 1},
      {1, 0, 0, 0}
    };
    f[0][0] = 1;
    for (int i = 0; i < n; i++)
      // 枚举当前状态
      for (int j = 0; j < 4; j++)
        // 枚举转移到的状态
        for (int k = 0; k < 4; k++)
          // 如果能转移，则累加方案数
          if (g[j][k]) f[i + 1][k] = (f[i + 1][k] + f[i][j]) % MOD;
    return f[n][0];
  }
};

时空复杂度$O(n)$。