王道数据结构6（图）

张张同学！

已于 2022-08-28 16:04:44 修改

阅读量1.3k

点赞数 3

分类专栏：王道数据结构文章标签：数据结构

于 2022-08-22 18:25:46 首次发布

本文链接：https://blog.csdn.net/qq_46126118/article/details/126471386

版权

王道数据结构专栏收录该内容

17 篇文章 11 订阅

订阅专栏

图

一.概念
- （一）基本概念
- （二）常考考点
二.图的储存结构（邻接矩阵法）
三. 储存结构（邻接表表示法）
四.拓展存储结构（十字链表，邻接多重表）
- 【1】十字链表（存储有向图）
- 【2】邻接多重表（存储无向图）
五. 图的基本操作
六.图的遍历

一.概念

（一）基本概念

定义：图G由顶点集V和边集E组成，记为G=(V,E),其中V(G)表示图G中顶点的有限非空集；E(G)表示图G中顶点之间的关系(边)集合。若V={V1,V2,……Vn}，则用|V|表示图G中顶点的个数，也称图G的阶，E={(u,v)|u∈V,v∈V}，用|E|表示图G中边的条数。
注意：线性表可以是空表，树可以是空树，但图不可以为空，即V一定是非空集。
无向图，有向图：有向图<u,v>，其中u表示弧尾，v表示弧头。
简单图：简单图：①不存在重复边，② 不存在顶点到自身的边。
多重图：图G中某两个结点之间的边数多于一条，又允许顶点通过同一条边和自己关联，则G为多重图。
度，入度，出度：① 无向图：在具有n个顶点，e条边的无向图中，全部顶点的度的和等于边数的2倍。②有向图：度之和入度＋出度，在具有n个顶点，e条边的有向图中，入度+出度=e。
路径，简单路径，路径长度：① 在路径序列中，顶点不重复出现的路径称为简单路径。②路径长度：路径上边的数目。
回路，简单回路：除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。
点到点到距离：从顶点u出发到顶点v的最短路径若存在，则此路径的长度称为u到v的距离。若u到v根本不存在路径，则记该距离为无穷（∞）。
连通图，强连通图：①若图G中任意两个顶点都是连通的，则称图G为连通图，否则称为非连通图。对于n个顶点的无向图G，若G是连通图，则至少有n-1条边，若G是非连通图，则最多可能有C2n-1。②若图中任何一项顶点都是强连通的，则称为图为强连通图。对于n个顶点的有向图G，若G是强连通图，则最少为n条边（形成回路）。
子图、生成子图：若包含所有顶点的子图，就称为生成子图。并不是任意几个点，任意几条边都能构成子图。
连通分量：无向图中极大连通子图【子图必须连通，且包含尽可能多的顶点和边】称为连通分量。
强连通分量：有向图中有极大强连通子图【子图必须强连通，同时保留尽可能多的边】称为有向图的强连通分量。
生成树：连通图的生成树是包含图中全部顶点的一个极小连通子图【边尽可能的小，但要保持连通】。若哦图中顶点数是n，则它的生成树含有n-1条边，对于生成树而言，若砍去一条边，则会变成非连通图，若加上一条边则会形成一个回路。
生成森林：在非连通图中，连通分量的生成树构成了非连通图的生成森林。
边的权，带权图（网）
无向完全图：无向图中任意两个顶点之间都存在边，若无向图的顶点数|V|=n，则|E|∈[0，C2n]=[0,n(n-1)/2]。
有向完全图：有向图中任意两个顶点之间都存在方向相反的两条弧。若有向图的顶点数|V|=n，则|E|∈[0，2C2n]=[0,n(n-1)]。
稀疏图，稠密图：一般来说|E|<|V|log|V|时，可以视G为稀疏图。
树：不存在回路，且连通的无向图，n个顶点的树，必有n-1条边。
有向树：一个顶点的入度为0，其余顶点的入度均有1的有向图，称为有向树。
n个顶点的图，若|E|>n-1,则一定有回路。

（二）常考考点

对于n个顶点的无向图G，
① 所有顶点的度之和=2|E|。
②若G为连通图，则至少有n-1条边，若|E|>n-1，则一定有回路。
③若G有非连通图，则最多可能有C2n-1条边。
④无向完全图共有C2n条边。
对于n个顶点的有向图G，
①所有顶点的出度之和=入度之和=|E|。
②所有顶点的度之和=2|E|。
③若G是强连通图，则最少有n条边（形成回路）。
③有向完全图共有2C2n条边。

二.图的储存结构（邻接矩阵法）

1.数组表示法

(1) 有向图，无向图的邻接矩阵
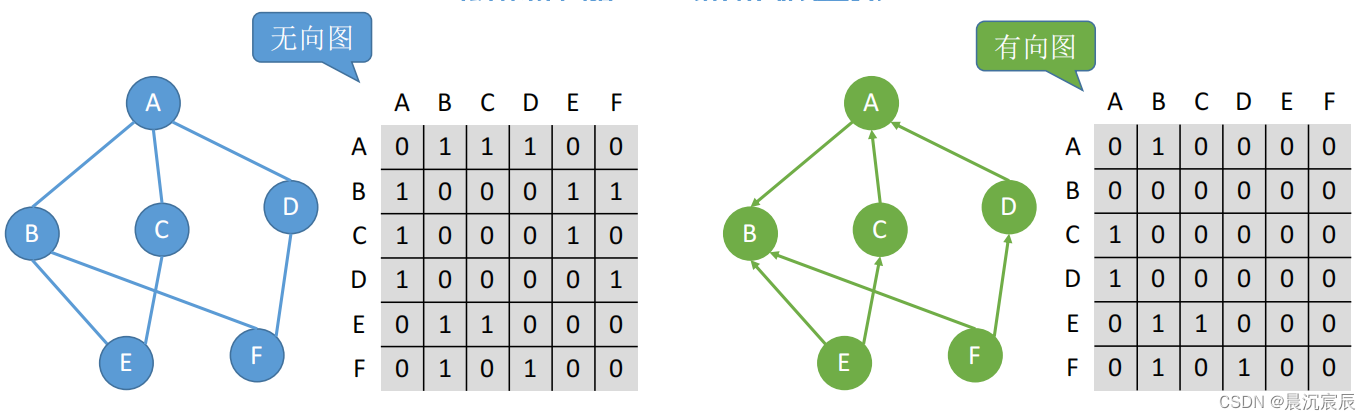
在这里插入图片描述
（2）网的邻接矩阵定义为：

a[i][j]:
（1） Wij 若<vi，vj> 或<vi，vj >∈VR

（2）∞ 反之

（3）说明：
① 对于无向图，顶点vi的度是邻接矩阵中第i行（或第i列）的元素之和， TD（vi）= ∑ a[i][j]。
② 对于有向图，顶点VI的出度OD（vi）是邻接矩阵中第i行的元素之和，顶点vi的出度ID（vi）是邻接矩阵中第j列）的元素之和。
③ 邻接矩阵法求顶点的度。入度。出度的时间复杂度为O(|V|)。
④ A² [1][2]:第一个顶点到第二个顶点路径为2的路径有多少条。

2. 定义邻接矩阵的结构

#define INFINITY INT_MAX
#define MAX_VERTEXT_NUM 20
typedef enum{DG,DN,AG,AN}GraphKind;
typedef struct ArcCell{
  VRType adj;//对无向图，用0,1表示是否相邻，对于带权图，为权值
  InfoType *info;//该弧相关信息的指针

}RrcCell,AdjMatrix[MAX_VERTEXT_NUM][MAX_VERTEXT_NUM];//邻接矩阵

3. 定义图的结构

（1）代码：

//定义图的结构
typedef struct {
   VertextType exs[MAX_VERTEXT_NUM]; //顶点
   AdjMatrix arcs[MAX_VERTEXT_NUM][MAX_VERTEXT_NUM]; //边的邻接矩阵
   int vexnum,arcnum; //个数
   GraphKind kind;//有向图？无向图？
}MGraph;

（3）注意：
① 邻接矩阵法的空间复杂度O(|V|2),之和顶点数有关
② 更适合存储稠密图
③对于无向图而言，因为是对称矩阵，可以进行压缩存储
（4）压缩存储

策略：只存储主对角线+下三角区
按行优先原则将各元素存入一堆数组中

B[0]	B[1]	B[2]	B[3]	B[4]	B[n(n+1)/2-1]
a1,1	a2,1	a2,2	a3,1	a3,2	an,n

aij->B[k]
ai,j = aj,i(由于对称性质)
k=(i(i-1))/2+j-1 [i≥j，属于下三角区和主对角线元素]
k=(j(j-1))/2+i-1 [i<j，属于上三角区]

4. 构造图G

status CreateGraph(MGraph &G)
{
    scanf(&G.kind)
    {
        case DG:return CreateDG(G);
         case DN:return CreateDN(G);
           case UDG:return CreateUDG(G);
             case UDN:return CreateDGN(G);
        default:return ERROR;
    }
}
//用无向图为例

status CreateUDN(MGraph &G)
{
    scanf(&G.arcnum,&G.vexnum,&IncInfo);//输入点数和边数
    //给顶点进行数字化编号
    for(i=0;i<G.vexnum;i++)
    { scanf(&G.exs[i]);//定义顶点数组（如果顶点本身就是1~n的数字无需这一步）
    }
    //初始化邻接矩阵
    for(i=0;i<G.vexnum;i++)
    {
        for(j=0;j<G.vexnum;j++)
        {
            G.arcs[i][j]={ININITY,NULL};
        }
    }
    //通过边数进行遍历
    for(k=0;k<G.arcnum;K++)
    {
        scanf(&V1,&V2,&W);//输入邻接的连个顶点
        i=locatteVex(G,V1);j=locateVex(G,V2);//查找V1,V2的位置
        G.arcs[i][j].adj=w;//给邻接矩阵赋值
        if(IncInfo)
        {
            INPUT(*G.arcs[i][j].info);
        }
        G.arcs[j][i]=G.arcs[i][j];//由于是无向图，对称
    }
    return ok;
}

5. 特点

优点：

无向图邻接矩阵是对称矩阵，同一条边表示了两次
顶点v的度：等于二维数组对应行(或列)中1的个数
判断两顶点v、u是否为邻接点：只需判二维数组对应分量是否为1
在图中增加、删除边：只需对二维数组对应分量赋值1或清0
占用存储空间只与它的顶点数有关，与边数无关；适用于边稠密的图
对有向图的数组表示法可做类似的讨论

缺点：

不便于删除和增加顶点
不便于统计边的数目，需要扫描邻接矩阵所有元素才能统计完毕，时间复杂度为O(n² )
空间复杂度高，对于有向图，n个顶点需要n² 个单元存储边，对于无向图，n(n-1)/2个单元，空间复杂度为O(n² )

三. 储存结构（邻接表表示法）

1. 储存方式

【1】无向图

把从一个顶点出发的边链接在一个单链表（又名边链表）中把从一个顶点出发的边链接在一个单链表（又名边链表）中
所有边链表的表头指针放在一个顺序表中
对于无向图而言，数据会有存在冗余，边结点的数量为2|E|，整体空间复杂度为O(|V|+2|E|)

【2】有向图

实例
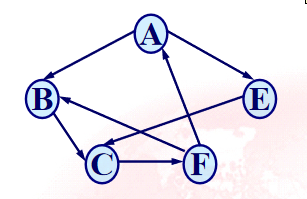
注意，在有向图的邻接表中不易找到指向该顶点的弧。
边结点的数量为|E|，整体空间复杂度为O(|V|+|E|)

2. 结构

【1】顶点的结点结构

———————
| data | firstarc |
———————

data数据域：储存顶点vi
firstarc链域：指向链表中第一个结点

【2】弧的结点结构

——————————
| adjvex | info | nextarc |
——————————

adjvex邻接点域：与顶点vi邻接的点在图中的位置
info数据域：储存和边相关的信息，如权值
nextarc链域：与顶点vi的点在图中的位置

3.图的邻接表存储表示（算法）

#define MAX_VERTEXT_NUM 20
//建立边结点 
typedef struct ArcNode {
      int adjvex;                      // 该弧所指向的顶点的位置
      struct ArcNode *nextarc; // 指向下一条弧
      InfoType  *info;                // 该弧相关信息（可选）
}ArcNode; 
// 顶点结点
typedef struct VNode{
        VertexType data;              // 顶点信息
        ArcNode  *firstarc;          // 指向第一条依附该顶点的弧
}VNode,AdjList[MAX_VERTEXT_NUM];
//邻接表
typedef struct {
      Adjlist vertices;
      int vexnum,arcnum;
      int kind;
}ALGraph;

//建立邻接表算法
//初始化一个结点总数为num的图，k为图的类型，num为结点总数
void InitG(ALGraph G,enum GraphKind k,int num)
{
    G.kind=k;
    G.vexnum=num;
    G.vertices=new VNode[vexnum];
    for(int i=0;i<G.vexnum;i++)
    {G.vertices[i].Firstarc=NULL;
        cin>>G.vertics[i].data;
    }
}

//有向图(网)增加弧的算法，将弧(from,to,weight)加入图
void InsertArc(ALGragh G,int from,int to,int weight)
{
    ArcNode *s=new ArcNode;
    s->weight=weight;
    s->adjvex=to;
    s->nextarc=G.vertices[from].firstarc;//插到链表vertices[from]的头
    G.vertices[from].firstarc=s;
}

4. 结论

（1）在邻接表中，同一条边对应两个结点。
（2）无向图中顶点v的度：等于v 对应的链表的长度；但是，在有向图中，要求顶点A的的入度，则需要遍历所有的顶点连接的链表，判断有几个存在顶点A；求出度，则是A顶点链表有几个点。
（3）判定两顶点v，w是否邻接：要看v对应的链表中有无对应的结点w（相反判断也行）；
（4）对于一个图，给定的邻接表是并不唯一的（区分与邻接矩阵）
（5）增减边：要在两个单链表插入、删除结点；
（6）占用存储空间与顶点数、边数均有关；适用于边稀疏的图

四.拓展存储结构（十字链表，邻接多重表）

【1】十字链表（存储有向图）

实例
空间复杂度：O(|V|+|E|)

【2】邻接多重表（存储无向图）

实例
解决无向图冗余信息的问题，空间大
删除边，删除结点操作更简单
空间复杂度：O(|V|+|E|)

五. 图的基本操作

【1】Adjacent(G,x,y)边的存在

思路：
①无向图：邻接矩阵，判断aij是否为1，邻接表，i点的邻接表是否有j点；
②有向图类似
时间复杂度

时间复杂度	邻接矩阵	邻接表
无向图	O(1)	O(1)~O(V)
有向图	O(1)	O(1)~O(V)

【2】Neighbors(G,x):列出图G中与结点x邻接的边

思路：
①无向图：邻接矩阵，罗列出x点的行为1的所有点，邻接表，遍历x的链表的所有结点；
②有向图：邻接矩阵，出边遍历行，入边遍历列，邻接表，(出边)遍历x的链表，(入边)遍历所有的结点查看哪个结点值是x。
时间复杂度

时间复杂度	邻接矩阵	邻接表
无向图	O(V)	O(1)~O(V)
有向图	O(V)	出边：O(1)~O(V) 入边：O(E)

【3】InsertVertex(G,x):在图G中插入顶点x

思路：
① 无向图：邻接矩阵，给矩阵增加一个x行增加一个x列；邻接表，给表的最后一行增加x项，不接任何一个结点，指向NULL。
② 有向图：类似
时间复杂度

时间复杂度	邻接矩阵	邻接表
无向图	O(1)	O(1)
有向图	O(1)	O(1)

【4】DeleteVertex(G,x):从图G中删除顶点x

思路：
① 无向图：邻接矩阵，将x的所有行列全部清空为-1，在顶点集中x的值表示为-1或false；邻接表，将所有与x有关的信息删除，需要遍历所有的结点。
② 有向图：邻接矩阵，与无向图类似，邻接表，删出边需要将x的链表都删除，删入边，需要遍历所有的结点。
时间复杂度

时间复杂度	邻接矩阵	邻接表
无向图	O(V)	O(1)~O(E)
有向图	O(V)	删出边：O(1)~O(V) 删入边：O(E)

【5】AddEdge(G,x,y):若无向边(x,y)或有向边<x,y>不存在，则向图G中添加该边。

思路：
① 无向图，邻接矩阵，将axy的值由0改为1，邻接表，将x的链表后或前加上结点y，最好使用头插法。
② 有向图，类似。

时间复杂度	邻接矩阵	邻接表
无向图	O(1)	O(1)
有向图	O(1)	O(1)~O(V)

【6】FirstNeighbor(G,x):求图G中顶点的第一个邻接点

思路
① 无向图：邻接矩阵，扫描x的一行第一个为1的元素，可能第一个就是也可能到最后一个都没有；邻接表，查看x链表的第一个结点。
② 有向图：邻接矩阵，找x有关的行列，也就是出边入边的第一个邻接点，邻接表，出边寻找简单，但是入边需要遍历所有的边。
时间复杂度

时间复杂度	邻接矩阵	邻接表
无向图	O(1)~O(V)	O(1)
有向图	O(1)~O(V)	找出边连接点：O(1) 找入边邻接点：O(1)~O(E)

【7】NextNeighbor(G,x,y):假设图G中顶点y是顶点x的一个邻接点，返回除y之外顶点x的下一个邻接点的顶点号，若y是x的最后一个邻接点，则返回-1

时间复杂度	邻接矩阵	邻接表
无向图	O(1)~O(V)	O(1)
有向图	O(1)	O(1)~O(V)

重点是 6、7

六.图的遍历

1. 图遍历的概述

1、定义——从某顶点出发，沿着一些边访问连通图中所有顶点，且使每个顶点仅访问一次的运算。
2、为避免重复访问，可设置辅助数组Visited[ ]，各分量初值为0，当顶点被访问，对应分量被置为1。
3、方法——深度优先（depth first search DFS）
广度优先（breadth first search BFS）

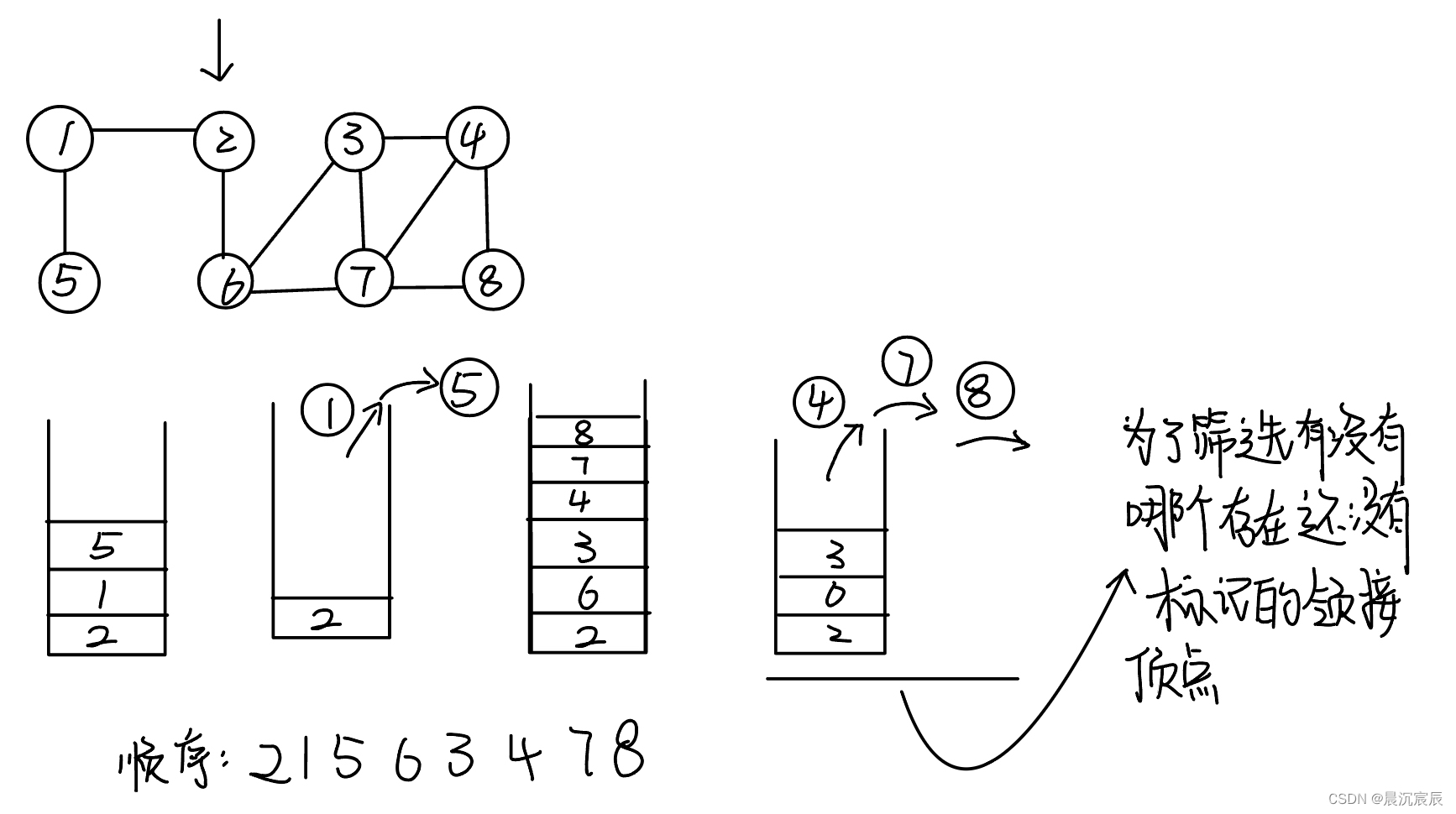
2.深度优先遍历（栈）

（1）算法描述

从图中某个顶点V0 出发，访问此顶点，然后依次从V0的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和V0有路径相通的顶点都被访问到。

从深度优先搜索遍历连通图的过程类似于树的先根遍历；
如何判别V的邻接点是否被访问？
解决的办法是：为每个顶点设立一个 “访问标志数组bool visited[vexnum]”。

（2）算法实现

邻接矩阵

int visited[MAX];//设置一个数组，判断是否遍历过，false/1为遍历过
void DFGTraverse(Graph G,int v)
{
    for(v=0;v<G.vexnum;v++)
       visited[v]=0;//初始化判断数组
    for(v=0;v<G.vexnum;v++)
    {
        if(!visited[v])//如果没有遍历过
            DFS(G,V);//进行遍历
    }
}
void DFS(Graph G,int v)//进行递归遍历
{
    visited[v]=1;printf(v);//改变判断数组，输出点
    for(w=FirstVex(G,v);w!=0;w=NextVex(G,v))//从每一行第一个邻接矩阵值为1的，跳转到下一个值为1的
    {
        if(!visited[w])
            DFS(G,v);
    }
}
int FirstVex(Graph G,int v)//判断第一个不是0的
{
    int i;
    for(i=0;i<G.vexnum;i++)
    {
        if(G.arcs[v][i]==1&&visited[i]==False)
            return i;
    }
    return -1;
}
void NextVex(Graph G,int v)//判断下一个不是0的
{
    int i;
    for(i=w;i<G.vexnum;i++)
    {
        if(G.arcs[v][i]==1&&visited[i]!=False)
            return i;
    }
    return -1;
}

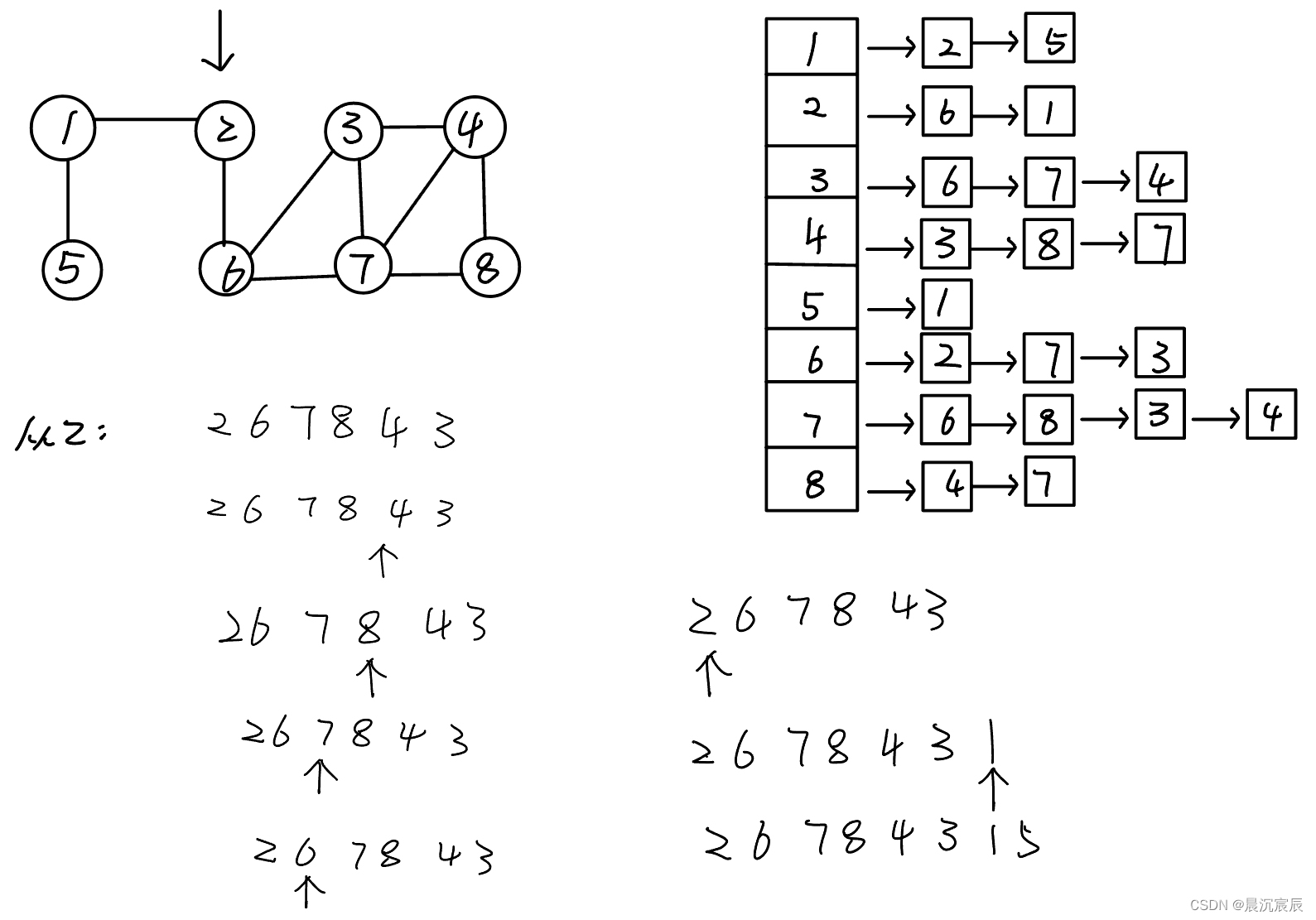
请添加图片描述

2.邻接表

void DFS(Graph G,int v)
{
    cout<<G.vertices[v].data<<"  ";
    visited[v]=true;
    ArcNode *p=G.vertices[v].firstarc;
    while(p!=NULL)
    {
        int w=p->adjvex;
        if(!visited[w])
            DFS(G,w);
        p=p->nextarc;a
    }
}

请添加图片描述

（3）时间/空间复杂度

空间复杂度：邻接矩阵，最坏情况O(|V|),最好情况O(1)。
时间复杂度：
T(V)=o(|V|²) 邻接矩阵
T(V)=O(|E|+n) 邻接表

3. 广度优先遍历

（1）算法描述

从图中某个顶点V0出发，并在访问此顶点之后依次访问V0的所有未被访问过的邻接点，之后按这些顶点被访问的先后次序依次访问它们的邻接点，直至图中所有和V0有路径相通的顶点都被访问到。
对于非连通图，可能此时尚有顶点未被访问，则另选图中一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
因此关键在于：①找到与一个顶点相邻的所有结点；② 标记哪些顶点被访问过；③ 需要一个辅助队列存储。

（2）例子

在这里插入图片描述

（3）算法

在这里插入图片描述

（4）代码

采用邻接表存储实现无向图的广度优先遍历

//visited是访问标记数组

//处理非连通图的情况 
bool BFSTraverse(Graph G){
	for(int i=0;i<G.vexnum;++i)
		visited[i] = false;
	InitQueue(Q);
	for(int i=0;i<G.vexnum;++i){
		if(!visited[i])
			BFS(G,i);
	}
}
 
void BFS(Graph G,int v){
	visit(v);				//访问v顶点 
	visited[v] = True;		//修改该顶点对应数组的值为true 
	EnQueue(Q,v);			//入队 
	while(!isEmpty(Q)){		//不空还有未遍历到的节点 
		DeQueue(Q,v);		//出队v 
		for(w = FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))		//找到所有符合条件的邻接节点 
			if(!visited[w]){		//w是否被访问 
				visit[w];			//访问 
				visited[w] = true;	//修改该顶点对应数组的值为true
				EnQueue(Q,w);		//入队 
			}
	}
}

bool BFSTraverse(Graph G，int v){
	for(int i=0;i<G.vexnum;++i)
		visited[i] = false;
	InitQueue(Q);
	for(int i=0;i<G.vexnum;++i){
		if(!visited[i])
				visit(v);				//访问v顶点 
				visited[v] = True;		//修改该顶点对应数组的值为true 
				EnQueue(Q,v);			//入队 
				while(!isEmpty(Q)){		//不空还有未遍历到的节点 
					DeQueue(Q,v);		//出队v 
					for(w = FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w))		//找到所有符合条件的邻接节点 
						if(!visited[w]){		//w是否被访问 
							visit[w];			//访问 
							visited[w] = true;	//修改该顶点对应数组的值为true
							EnQueue(Q,w);		//入队 
						}
				}
		}
}

（5）分析

① 如果使用邻接表，则从同一个顶点广度优先遍历序列会随着链接表不同而不同，但是由于邻接矩阵是唯一的，所以从同一个广度优先遍历得到的顺序是唯一的。
② 对于无向图，调用BFS函数的次数=连通分量数
③ 空间复杂度：O(|V|)
④ 时间复杂度：
a.使用邻接矩阵存储的图：访问|V|个顶点的需要O(|V|)的时间，查找每个顶点的邻接点都需要O(|V|)的时间，而总共有|V|个顶点，时间复杂度=O(|V|2)+o(|V|)=O(|V|2)。
b.使用邻接表的图：访问|V|个顶点的需要O(|V|)的时间，查找各个顶点的邻接点都需要O(|E|)的时间，时间复杂度=O(|V|)+o(|E|)。

（6）广度优先生成树（森林）

① 通过广度优先遍历可以的得到一棵遍历树
② 由于邻接表不唯一，则树不唯一；由于邻接矩阵唯一，则树唯一。
伞遍历非连通图，可以得到广度优先生成森林。

4. 规律

（1）对于无向图而言，调用BFS/DFS的次数=连通分量数。
（2）对于有向图而言，若起始顶点到其他顶点都有路径，则只需调用一次BFS/DFS函数。对于强连通图，从任一结点出发只需调用1次BFS/DFS函数。

张张同学！

关注

3
点赞
踩
17

收藏

觉得还不错? 一键收藏
0
评论
王道数据结构6（图）

/对无向图，用0,1表示是否相邻，对于带权图，为权值 InfoType * info;//该弧相关信息的指针 } RrcCell , AdjMatrix [ MAX_VERTEXT_NUM ] [ MAX_VERTEXT_NUM ];//邻接矩阵20//对无向图，用0,1表示是否相邻，对于带权图，为权值 InfoType * info;//该弧相关信息的指针 } RrcCell , AdjMatrix [ MAX_VERTEXT_NUM ] [ MAX_VERTEXT_NUM ];.........
复制链接

扫一扫