
一、卡尔曼滤波公式(KF)
卡尔曼滤波是一种最优化递归数据处理算法。(Optimal Recursive Data Processing Algorithm)
Kalman滤波是时域滤波,采用状态空间描述系统,运用递推形式是计算简单,数据存储量小,应用广泛。
广泛应用于惯性导航、制导系统、全球定位系统、目标跟踪、通信与信号处理、金融等。
Kalman滤波器的广泛应用是因为我们的生活中存在大量不确定性。
在我们描述一个系统时,不确定性主要体现在3个方面:
- 不存在完美的数学模型
- 系统的扰动不可控,也很难建模
- 测量传感器本身存在误差
Kalman滤波算法,该算法是在线性高斯下的最优滤波估计算法。
1.1公式推导
状态空间方程:
x
k
=
A
x
k
−
1
+
B
u
k
−
1
+
w
k
−
1
(1)
x_k=Ax_{k-1}+Bu_{k-1}+w_{k-1} \tag{1}
xk=Axk−1+Buk−1+wk−1(1)
z
k
=
H
x
k
+
v
k
(2)
z_k=Hx_k+v_k \tag{2}
zk=Hxk+vk(2)
- w k − 1 w_{k-1} wk−1为过程噪声,不可测,但我们可以假设其符合正态分布 P ( w ) ∼ ( 0 , Q ) P(w)\sim(0,Q) P(w)∼(0,Q),0为期望,Q为协方差矩阵。 Q = E [ w w T ] Q=E[ww^T] Q=E[wwT]
- v k v_k vk为测量噪声。 P ( v ) ∼ ( 0 , R ) P(v)\sim(0,R) P(v)∼(0,R), R = E [ v v T ] R=E[vv^T] R=E[vvT]
- 在实际建模过程中, w k − 1 w_{k-1} wk−1和 v k v_k vk项是无法建模的,只知道前面的项,所以只能有估计值。
x ^ k − = A x k − 1 + B u k − 1 (3) \hat x_k^-=Ax_{k-1}+Bu_{k-1}\tag{3} x^k−=Axk−1+Buk−1(3)
- x ^ k − \hat x_k^- x^k−为先验估计,通过状态空间方程去掉过程噪声得到的式子,是计算出来的。
由 z k = H x k z_k=Hx_k zk=Hxk可得 x ^ k M E A = H − 1 z k (4) \hat x_{k_{MEA}}=H^{-1}z_k\tag{4} x^kMEA=H−1zk(4)
- 测量结果 z k z_k zk已知, x ^ k M E A \hat x_{k_{MEA}} x^kMEA是测出来的。
无论是算出来的
x
^
k
−
\hat x_k^-
x^k−还是测出来的
x
^
k
M
E
A
\hat x_{k_{MEA}}
x^kMEA,都不具备噪声项,利用数据融合可得
x
^
k
=
x
^
k
−
+
G
(
H
−
1
z
k
−
x
k
−
)
,
G
=
K
k
H
\hat x_k=\hat x_k^-+G(H^{-1}z_k-x_k^-),G=K_kH
x^k=x^k−+G(H−1zk−xk−),G=KkH
- G = 0 G=0 G=0时, x ^ k = x ^ k − \hat x_k=\hat x_k^- x^k=x^k−
- G = 1 G=1 G=1时, x ^ k = H − 1 z k \hat x_k=H^{-1}z_k x^k=H−1zk
x ^ k = x ^ k − + K k ( z k − H x k − ) (5) \hat x_k=\hat x_k^-+K_k(z_k-Hx_k^-)\tag{5} x^k=x^k−+Kk(zk−Hxk−)(5)
- K k = 0 K_k=0 Kk=0时, x ^ k = x ^ k − \hat x_k=\hat x_k^- x^k=x^k−
- K k = H − K_k=H^- Kk=H−时, x ^ k = H − 1 z k \hat x_k=H^{-1}z_k x^k=H−1zk
目标:寻找
K
k
K_k
Kk使得
x
^
k
→
x
k
\hat x_k\to x_k
x^k→xk,
x
k
x_k
xk为实际值。
引入
e
k
=
x
k
−
x
^
k
(6)
e_k=x_k-\hat x_k\tag{6}
ek=xk−x^k(6)
-
P ( e k ) ∼ ( 0 , P ) P(e_k)\sim(0,P) P(ek)∼(0,P)
P = E [ e e T ] = [ σ e 1 2 σ e 1 σ e 2 σ e 2 σ e 1 σ e 2 2 ] (7) P=E[ee^T]=\begin{bmatrix}\sigma e_1^2 & \sigma e_1\sigma e_2 \\ \sigma e_2\sigma e_1 & \sigma e_2^2 \end{bmatrix} \tag{7} P=E[eeT]=[σe12σe2σe1σe1σe2σe22](7) -
t r ( P ) = σ e 1 2 + σ e 2 2 tr(P)=\sigma e_1^2+\sigma e_2^2 tr(P)=σe12+σe22,目标即为使得 t r ( P ) tr(P) tr(P)最小
x k − x ^ k = 【代入 ( 5 ) 】 x k − ( x ^ k − + K k ( z k − H x k − ) ) = x k − x k − − K k z k + K k H x k − = 【代入 ( 2 ) 】 x k − x k − − K k ( H x k + v k ) + K k H x k − = ( I − K k H ) ( x k − x k − ) − K k v k = ( I − K k H ) e k − − K k v k \begin{aligned} \color{green}x_k-\hat x_k&=【代入(5)】x_k-(\hat x_k^-+K_k(z_k-Hx_k^-)) \\&=x_k-x_k^--K_kz_k+K_kHx_k^- \\&=【代入(2)】x_k-x_k^--K_k(Hx_k+v_k)+K_kHx_k^- \\&=(I-K_kH)(x_k-x_k^-)-K_kv_k \\&= \color{green}(I-K_kH)e_k^--K_kv_k \end{aligned} xk−x^k=【代入(5)】xk−(x^k−+Kk(zk−Hxk−))=xk−xk−−Kkzk+KkHxk−=【代入(2)】xk−xk−−Kk(Hxk+vk)+KkHxk−=(I−KkH)(xk−xk−)−Kkvk=(I−KkH)ek−−Kkvk
E [ ( I − K k H ) e k − v k T K k T ] = ( I − K k H ) E ( e k − v k T ) K k T = ( I − K k H ) E ( e k − ) E ( v k T ) K k T 【 E ( e k − ) = 0 , E ( v k T ) = 0 】 = 0 \begin{aligned}\color{blue}E[(I-K_kH)e_k^-v_k^TK_k^T]&=(I-K_kH)E(e_k^-v_k^T)K_k^T \\&=(I-K_kH)E(e_k^-)E(v_k^T)K_k^T \ \ \ 【E(e_k^-)=0,E(v_k^T)=0】 \\&=\color{blue}0 \end{aligned} E[(I−KkH)ek−vkTKkT]=(I−KkH)E(ek−vkT)KkT=(I−KkH)E(ek−)E(vkT)KkT 【E(ek−)=0,E(vkT)=0】=0
E [ K k v k e k − T ( I − K k H ) T ] = 0 【理由同上】 \color{blue}E[K_kv_ke_k^{-T}(I-K_kH)^T]=\color{blue}0【理由同上】 E[Kkvkek−T(I−KkH)T]=0【理由同上】
P k = E [ e e T ] = E [ ( x k − x ^ k ) ( x k − x ^ k ) T ] = E [ [ ( I − K k H ) e k − − K k v k ] [ ( I − K k H ) e k − − K k v k ] T ] = E [ [ ( I − K k H ) e k − − K k v k ] [ e k − T ( I − K k H ) T − v k T K k T ] ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T − ( I − K k H ) e k − v k T K k T − K k v k e k − T ( I − K k H ) T + K k v k v k T K k T ] = E [ ( I − K k H ) e k − e k − T ( I − K k H ) T ] − E [ ( I − K k H ) e k − v k T K k T ] − E [ K k v k e k − T ( I − K k H ) T ] + E [ K k v k v k T K k T ] = ( I − K k H ) E ( e k − e k − T ) ( I − K k H ) T + K k E ( v k v k T ) K k T = 【 E ( e k − e k − T ) = P k − , E ( v k v k T ) = R 】( P k − − K k H P k − ) ( I − K k H ) T + K k R K k T = P k − − K k H P k − − P k − H T K k T + K k H P k − H T K k T + K k R K k T \begin{aligned} P_k & =E[ee^T] \\ &=E[({\color{green}x_k-\hat x_k})({\color{green}x_k-\hat x_k})^T] \\ &=E[[(I-K_kH)e_k^--K_kv_k][(I-K_kH)e_k^--K_kv_k]^T] \\ &=E[[(I-K_kH)e_k^--K_kv_k][e_k^{-T}(I-K_kH)^T-v_k^TK_k^T]] \\ &=E[(I-K_kH)e_k^-e_k^{-T}(I-K_kH)^T-(I-K_kH)e_k^-v_k^TK_k^T-K_kv_ke_k^{-T}(I-K_kH)^T+K_kv_kv_k^TK_k^T] \\ &=E[(I-K_kH)e_k^-e_k^{-T}(I-K_kH)^T]-{\color{blue}E[(I-K_kH)e_k^-v_k^TK_k^T]}-{\color{blue}E[K_kv_ke_k^{-T}(I-K_kH)^T]}+E[K_kv_kv_k^TK_k^T] \\ &=(I-K_kH)E(e_k^-e_k^{-T})(I-K_kH)^T+K_kE(v_kv_k^T)K_k^T \\ &=【E(e_k^-e_k^{-T})=P_k^-,E(v_kv_k^T)=R】(P_k^--K_kHP_k^-)(I-K_kH)^T+K_kRK_k^T \\ &=P_k^--{\color{purple}K_kHP_k^-}-{\color{red}P_k^-H^TK_k^T}+K_kHP_k^-H^TK_k^T+K_kRK_k^T \end{aligned} Pk=E[eeT]=E[(xk−x^k)(xk−x^k)T]=E[[(I−KkH)ek−−Kkvk][(I−KkH)ek−−Kkvk]T]=E[[(I−KkH)ek−−Kkvk][ek−T(I−KkH)T−vkTKkT]]=E[(I−KkH)ek−ek−T(I−KkH)T−(I−KkH)ek−vkTKkT−Kkvkek−T(I−KkH)T+KkvkvkTKkT]=E[(I−KkH)ek−ek−T(I−KkH)T]−E[(I−KkH)ek−vkTKkT]−E[Kkvkek−T(I−KkH)T]+E[KkvkvkTKkT]=(I−KkH)E(ek−ek−T)(I−KkH)T+KkE(vkvkT)KkT=【E(ek−ek−T)=Pk−,E(vkvkT)=R】(Pk−−KkHPk−)(I−KkH)T+KkRKkT=Pk−−KkHPk−−Pk−HTKkT+KkHPk−HTKkT+KkRKkT
( P k − H T K k T ) T = K k ( P k − H T ) T = K k H P k − 【故这两项的迹相等】 \begin{aligned}({\color{red}P_k^-H^TK_k^T})^T&=K_k(P_k^-H^T)^T \\&={\color{purple}K_kHP_k^-} 【故这两项的迹相等】 \end{aligned} (Pk−HTKkT)T=Kk(Pk−HT)T=KkHPk−【故这两项的迹相等】
t r ( P k ) = t r ( P k − ) − 2 t r ( K k H P k − ) + t r ( K k H P k − H T K k T ) + t r ( K k R K k T ) tr(P_k)=tr(P_k^-)-2tr(K_kHP_k^-)+tr(K_kHP_k^-H^TK_k^T)+tr(K_kRK_k^T) tr(Pk)=tr(Pk−)−2tr(KkHPk−)+tr(KkHPk−HTKkT)+tr(KkRKkT)
d t r ( P k ) d K k = 0 − 2 ( H P k − ) T + 2 K k H P k − H T + 2 K k R \frac{dtr(P_k)}{dK_k}=0-2(HP_k^-)^T+2K_kHP_k^-H^T+2K_kR dKkdtr(Pk)=0−2(HPk−)T+2KkHPk−HT+2KkR
令
d
t
r
(
P
k
)
d
K
k
=
0
\frac{dtr(P_k)}{dK_k}=0
dKkdtr(Pk)=0得
−
2
(
H
P
k
−
)
T
+
2
K
k
H
P
k
−
H
T
+
2
K
k
R
=
0
-2(HP_k^-)^T+2K_kHP_k^-H^T+2K_kR=0
−2(HPk−)T+2KkHPk−HT+2KkR=0
−
P
k
−
T
H
T
+
K
k
H
P
k
−
H
T
+
K
k
R
=
0
-P_k^{-T}H^T+K_kHP_k^-H^T+K_kR=0
−Pk−THT+KkHPk−HT+KkR=0
【协方差矩阵的转置等于其本身】
【协方差矩阵的转置等于其本身】
【协方差矩阵的转置等于其本身】
−
P
k
−
H
T
+
K
k
H
P
k
−
H
T
+
K
k
R
=
0
-P_k^-H^T+K_kHP_k^-H^T+K_kR=0
−Pk−HT+KkHPk−HT+KkR=0
K
k
(
H
P
k
−
H
T
+
R
)
=
P
k
−
H
T
K_k(HP_k^-H^T+R)=P_k^-H^T
Kk(HPk−HT+R)=Pk−HT
K
k
=
P
k
−
H
T
H
P
k
−
H
T
+
R
K_k=\frac{P_k^-H^T}{HP_k^-H^T+R}
Kk=HPk−HT+RPk−HT
- R较大时, K k → 0 , x ^ k = x ^ k − K_k \to 0,\hat x_k=\hat x_k^- Kk→0,x^k=x^k−
- R较小时, K k = H − , x ^ k = H − 1 z k K_k=H^-,\hat x_k=H^{-1}z_k Kk=H−,x^k=H−1zk
e k − = x k − x ^ k − = A x k − 1 + B u k − 1 + w k − 1 − A x ^ k − 1 − B u k − 1 = A ( x k − 1 − x ^ k − 1 ) + w k − 1 = A e k − 1 + w k − 1 \begin{aligned}{\color{brown}e_k^-}&=x_k-\hat x_k^- \\ &=Ax_{k-1}+Bu_{k-1}+w_{k-1}-A\hat x_{k-1}-Bu_{k-1} \\ &=A(x_{k-1}-\hat x_{k-1})+w_{k-1} \\ &=\color{brown}Ae_{k-1}+w_{k-1} \end{aligned} ek−=xk−x^k−=Axk−1+Buk−1+wk−1−Ax^k−1−Buk−1=A(xk−1−x^k−1)+wk−1=Aek−1+wk−1
E [ A e k − 1 w k − 1 T ] = 【相互独立】 A E [ e k − 1 ] E [ w k − 1 T ] = 【 E [ e k − 1 ] = 0 , E [ w k − 1 T = 0 】 A ⋅ 0 ⋅ 0 = 0 \begin{aligned}{\color{fuchsia}E[Ae_{k-1}w_{k-1}^T]}&=【相互独立】AE[e_{k-1}]E[w_{k-1}^T] \\&=【E[e_{k-1}]=0,E[w_{k-1}^T=0】A\cdot0\cdot0 \\&=\color{fuchsia}0 \end{aligned} E[Aek−1wk−1T]=【相互独立】AE[ek−1]E[wk−1T]=【E[ek−1]=0,E[wk−1T=0】A⋅0⋅0=0
E [ w k − 1 e k − 1 T A T ] = 0 【理由同上】 \color{fuchsia}E[w_{k-1}e_{k-1}^TA^T]=0【理由同上】 E[wk−1ek−1TAT]=0【理由同上】
P k − = E [ e k − e k − T ] = E [ ( A e k − 1 + w k − 1 ) ( A e k − 1 + w k − 1 ) T ] = E [ A e k − 1 e k − 1 T A T + A e k − 1 w k − 1 T + w k − 1 e k − 1 T A T + w k − 1 w k − 1 ) T ] = E [ A e k − 1 e k − 1 T A T ] + E [ A e k − 1 w k − 1 T ] + E [ w k − 1 e k − 1 T A T ] + E [ w k − 1 w k − 1 ) T ] = E [ A e k − 1 e k − 1 T A T ] + E [ w k − 1 w k − 1 ) T ] = A E [ e k − 1 e k − 1 T ] A T + E [ w k − 1 w k − 1 ) T ] = A P k − 1 A T + Q \begin{aligned}P_k^- &=E[{\color{brown}e_k^-}e_k^{-T}] \\&=E[(Ae_{k-1}+w_{k-1})(Ae_{k-1}+w_{k-1})^T] \\&=E[Ae_{k-1}e_{k-1}^TA^T+Ae_{k-1}w_{k-1}^T+w_{k-1}e_{k-1}^TA^T+w_{k-1}w_{k-1})^T] \\&=E[Ae_{k-1}e_{k-1}^TA^T]+{\color{fuchsia}E[Ae_{k-1}w_{k-1}^T]}+{\color{fuchsia}E[w_{k-1}e_{k-1}^TA^T]}+E[w_{k-1}w_{k-1})^T] \\&=E[Ae_{k-1}e_{k-1}^TA^T]+E[w_{k-1}w_{k-1})^T] \\&=AE[e_{k-1}e_{k-1}^T]A^T+E[w_{k-1}w_{k-1})^T] \\&=AP_{k-1}A^T+Q \end{aligned} Pk−=E[ek−ek−T]=E[(Aek−1+wk−1)(Aek−1+wk−1)T]=E[Aek−1ek−1TAT+Aek−1wk−1T+wk−1ek−1TAT+wk−1wk−1)T]=E[Aek−1ek−1TAT]+E[Aek−1wk−1T]+E[wk−1ek−1TAT]+E[wk−1wk−1)T]=E[Aek−1ek−1TAT]+E[wk−1wk−1)T]=AE[ek−1ek−1T]AT+E[wk−1wk−1)T]=APk−1AT+Q
利用卡尔曼滤波器估计状态变量的值

1.2 代码实现
在这里插入代码片
二、扩展卡尔曼滤波(EKF)
EKF算法是将非线性函数以泰勒级数展开的方式,保留一阶项实现对非线性函数线性化,用雅可比矩阵代替卡尔曼滤波方程中的状态转移矩阵,然后以卡尔曼滤波算法为框架计算系统的状态估计值和方差。
对于非线性系统:
x
k
=
f
(
x
k
−
1
,
u
k
−
1
,
w
k
−
1
)
x_k=f(x_{k-1},u_{k-1},w_{k-1})
xk=f(xk−1,uk−1,wk−1)
z
k
=
h
(
x
k
,
v
k
)
z_k=h(x_k,v_k)
zk=h(xk,vk)
由于正态分布的随机变量通过非线性系统后就不再是正态的了,所以如果想使用Kalman滤波,就需要对其线性化。使用Tylor Series(泰勒级数)展开。
f
(
x
)
=
f
(
x
0
)
+
∂
f
∂
x
(
x
−
x
0
)
f(x)=f(x_0)+\frac{\partial f}{\partial x}(x-x_0)
f(x)=f(x0)+∂x∂f(x−x0)
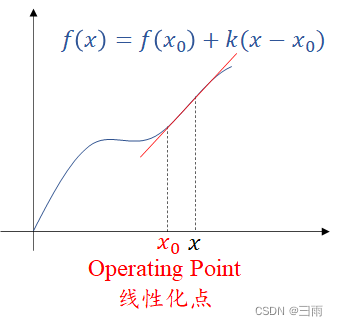
系统有误差,无法在真实点线性化。
f
(
x
k
)
f(x_k)
f(xk)在
x
^
k
−
1
\hat x_{k-1}
x^k−1(
k
−
1
k-1
k−1时的后验估计)处线性化
x
k
=
f
(
x
^
k
−
1
,
u
k
−
1
,
w
k
−
1
)
+
A
(
x
k
−
x
^
k
−
1
)
+
w
k
w
k
−
1
x_k={\color{red}f(\hat x_{k-1},u_{k-1},w_{k-1})}+{\color{green}A(x_k-\hat x_{k-1})}+{\color{blue}w_kw_{k-1}}
xk=f(x^k−1,uk−1,wk−1)+A(xk−x^k−1)+wkwk−1
- f ( x ^ k − 1 , u k − 1 , w k − 1 ) = f ( x ^ k − 1 , u k − 1 , 0 ) = x ~ k \color{red}f(\hat x_{k-1},u_{k-1},w_{k-1})=f(\hat x_{k-1},u_{k-1},0)=\tilde x_k f(x^k−1,uk−1,wk−1)=f(x^k−1,uk−1,0)=x~k
- A 为雅可比矩阵, A = ∂ f ∂ x ∣ x ^ k − 1 , u k − 1 \color{green}A为雅可比矩阵,A=\frac{\partial f}{\partial x}_{|\hat x_{k-1},u_{k-1}} A为雅可比矩阵,A=∂x∂f∣x^k−1,uk−1
- w k = ∂ f ∂ w ∣ x ^ k − 1 , u k − 1 \color{blue}w_k=\frac{\partial f}{\partial w}_{|\hat x_{k-1},u_{k-1}} wk=∂w∂f∣x^k−1,uk−1
z
k
z_k
zk在
x
~
k
\tilde x_k
x~k线性化
z
k
=
h
(
x
~
k
,
v
k
)
+
H
(
x
k
−
x
~
k
)
+
V
v
k
z_k=h(\tilde x_k,v_k)+H(x_k-\tilde x_k)+Vv_k
zk=h(x~k,vk)+H(xk−x~k)+Vvk

三、无迹卡尔曼滤波(UKF)
UKF算法是利用UT变换获取Sigma点集,然后通过非线性函数传递,将非线性函数线性化问题转换成系统状态量概率密度分布的近似,然后基于Kalman算法框架实现滤波问题。
UT变换,通过一定的采样策略,获取一组Sigma采样点,并设定相应的均值权值和方差权值,来近似非线性函数的后验均值和方差。
四、容积卡尔曼滤波(CKF)
CKF算法是基于三阶球面-径向容积准则,使用一组容积点来逼近具有加性高斯白噪声的非线性系统的状态均值和协方差。
三阶球面-径向容积规则是依据先验均值和协方差,通过容积规则选取容积点,再将这些容积点经过非线性函数的传递,再将非线性函数传递后的容积点加权处理近似状态后验均值和协方差。
五、几种方法对比
| 算法 | 优点 | 缺点 |
|---|---|---|
| EKF | 结构简单,适用于非线性程度不高的系统 | 由于忽略了高阶项,当非线性程度高或初始误差较大时,会大大降低滤波精度甚至发散 。 |
| UKF | 不会引入线性化误差,精度可以达到泰勒级数展开的二阶精度,无需计算雅克比矩阵,适合于不可或不连续的情况 | 当维数大于3时会损失掉部分Sigma点对非线性函数后验分布的统计特性,会使系统的估计精度有所下降。 |
| CKF | 实现简单,滤波精度高,收敛性好。 | CKF算法对非线性系统估计时舍去了部分近似化误差, 会造成滤波不满足拟一致性, 从而无法对状态真值进行准确估计。有时也会出现开方失败的问题。 |
参考:
[1]卡尔曼滤波DR_CAN
[2]https://blog.csdn.net/gangdanerya/article/details/105066174
[3]黄蔚. CKF及鲁棒滤波在飞行器姿态估计中的应用研究[D].哈尔滨工程大学,2018.
[4]https://blog.csdn.net/O_MMMM_O/article/details/106078679
导航
[5]https://blog.csdn.net/u011341856/article/details/114262451
https://gitcode.com/zm0612/eskf-gps-imu-fusion/tree/main
https://blog.csdn.net/qq_38650944/article/details/123594568
https://blog.csdn.net/qq_38650944/article/details/123580686
https://www.guyuehome.com/13948






















 313
313











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








