机器学习 三：欠拟合，过拟合 & 偏差-方差权衡（Bias-Variance Tradeoff）

一、欠拟合与过拟合

一言以蔽之，欠拟合就是模型太简单，不能良好得描述出数据的真实分布。过拟合就是模型太复杂，不仅适应了所有的训练数据，且学习了训练数据中的噪声，导致模型缺少良好的泛化性（无法适应新数据）。

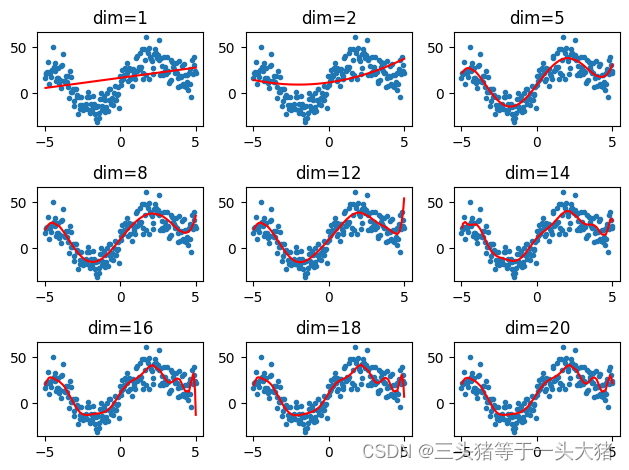
见下图，使用多项式回归法拟合随机生成的，符合类似三角函数且带有噪音的数据点。dim表示多项式的最高幂。易得：dim不够大时（dim=1 dim=2），模型拟合效果不好，即欠拟合。dim过大时（dim≥12）过度拟合数据点，导致同样偏离了真实的函数。

二、偏差与方差

bias 偏差：预测值与真值之间的差距，公式稍后介绍

variance 方差：与统计里的方差同一个意思。代表预测值分布的方差

对于符合某一模型（y = f(x)）的数据，在实际获取数据的时候，不可避免的，数据点会受到噪音(z)影响（y = f(x) + z），导致实际得到的数据点并不完全按照该模型分布。比如上图，模型是某个三角函数，但实际得到的数据点有噪音。

在针对有噪音的数据时，如何评判我们构建的模型与实际模型之间的差异？此处以MSE为例。

对于单个数据点的预测误差有如下公式，其中代表预测值，y代表真值。

则MSE有如下公式（注意此处是针对测试集得到，因此y与独立，且假设噪音z~N(0, sigma^2)）：

由此定义，

bias即模型预测与真值之间的差异，variance即模型经过多组训练数拟合出来的结果之间的差异。irreducible_noise代表无法避免的噪音。

用一张经典图来描述：

bias与variance之间，随着模型复杂度的提升，有如下此消彼长的关系（无法避免）：

因此，在训练模型时，所谓的最优解，即两者均相对较小的状态。在训练过程中，由于只考虑bias，因此过于充分的训练（模型太复杂），导致bias非常小，但实际variance便会非常大。这也就是前文提到的过拟合。此外，由上述公式还注意到，测试集上的误差同时考虑了bias与variance，因此也解释了模型在测试集的表现通常不如训练集的原因。

总结

过拟合=低bias&高variance，

欠拟合=高bias&低variance。

解决办法

欠拟合：

1 提高模型复杂度

2 扩展数据维度

过拟合：

1 扩充数据集

2 降低数据维度

3 正则化