GNSS单点定位解算与原理（基于MATLAB）

基于MATLAB的GNSS单点定位解算

1、间接平差原理：

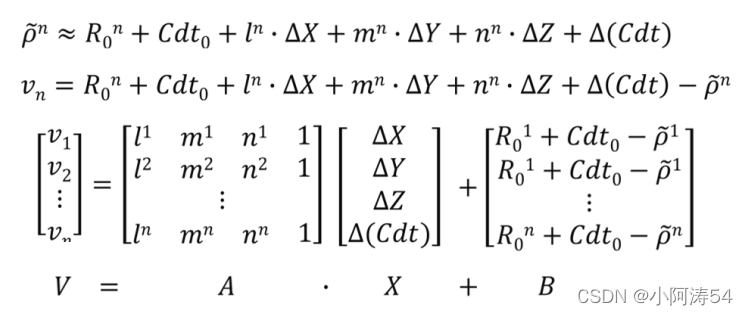
2.代码部分

% 已知伪距观测值，卫星坐标
% GNSS单点定位解算
% 已知X,Y,Z卫星坐标，和伪距P
P = [24115224.586, 23852690.710, 22389912.802, 24577319.825, 23384340.177, 24479081.841]';
X = [4791839.793, 24513555.750, 14424694.880, 2438267.619, 24699645.220, 20750469.480];
Y = [-16027953.710, 2290238.988, -12687500.250, -27845730.100, -2345295.901, -18429010.410];
Z = [23259013.420, 14685609.220, 20602453.000, 3484060.793, 14750395.800, -7962146.345];
% S是X, Y, Z的坐标 合矩阵
S = [X; Y; Z];
% 用来计算迭代次数的num
num = 0;
% 接收机坐标的初始值设为（0, 0, 0）
site_0 = [0 0 0 0]'; %分别是X0 Y0 Z0 Cdt
% 给需要用到的参数预先分配内存
Rs = zeros(1, 6);% 站星距
l = zeros(1, 6);
m = zeros(1, 6);
n = zeros(1, 6);
dCdt = zeros(1, 6);
f = zeros(1, 6);

% 迭代开始
while 1
    for t=1:6                         % 此处利用向量的方式更好
       % 循环计算第t个卫星的站星距离
       Rs(t) = sqrt((S(1, t)-site_0(1, 1))^2 + (S(2, t) - site_0(2, 1))^2 + (S(3, t) - site_0(3, 1))^2);
       
       % 由于接收机钟差造成的距离误差Cdt取一个值
       % 计算第t个站星距离的泰勒展开式中的偏导数l, m, n, dCdt = 1;
       l(t) = (site_0(1, 1)-S(1, t))./Rs(t);
       m(t) = (site_0(2, 1)-S(2, t))./Rs(t);
       n(t) = (site_0(3, 1)-S(3, t))./Rs(t);
       dCdt(t) = 1;
       %计算自由项
       f(t) = P(t)-Rs(t)+site_0(4); %s ite_0（4)是Cdt
    end
    % 循环进入下一颗卫星
    % 待到1-6个卫星都被计算后 ，将所有的卫星的系数组成误差方程，以(x, y, z, cdt)为未知数进行求解 
    A = [l', m', n', dCdt'];
    L = f';
    X = (inv(A'*A))*(A'*L);
    V = A*X-L;
    Xi = site_0 + X;
    % 如果deltaX小于0.001，则说明上述所计算的接收机坐标基本接近实际值，则结束迭代，反之用本次计算出的接收机坐标重新循环迭代
    if abs(X(1, 1)) > 0.001||abs(X(2, 1)) > 0.001||abs(X(3, 1)) > 0.001
        site_0 = Xi;                      % 把本次用到的坐标赋值给site_0，以便下次循环
        num = num + 1;
    else
        site_0 = Xi;                      % 求得满足条件的XYZ，结束迭代
        break;
    end
end
    % 输出卫星坐标
    Xr = site_0(1:3, 1);
    fprintf('计算所得接收机的坐标为：[%.3f, %.3f ,%.3f]',Xr);
    fprintf('\n');
    % 输出站星距离
    disp('站星距离为: ')
    t = 1:6;
    Pr(t) = sqrt((S(1,t) - site_0(1,1)).^2+(S(2, t) - site_0(2,1)).^2+(S(3,t)-site_0(3,1)).^2)+site_0(4)
    %接收机钟差
    fprintf('\n');
    disp('接收机钟差:')
    site_0(4)/(3e+08)

3.最终结果：

4.间接平差C语言：C语言间接平差