7-5 流水作业调度 (10 分)(思路+详解+johnson解析)Come Baby!!!!!!!!!!

一：题目

n个作业{1，2，…，n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。流水作业调度问题要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少。

输入格式:
第一行给出作业个数n(0<n<100)

第二行起的n行，每行两个数ai和bi

输出格式:
两个数字，以空格分隔，分别表示M1机器运行结束的时间和M2机器运行结束的时间。

输入样例:

6
30 80
120 100
50 90
20 60
90 30
110 10

结尾无空行
输出样例:

420 430

二：思路

1.判断动态规划：
首先m1的加工结束时间就是所有的时间和，但m2的加工时间和最小值，
求解过程是跳跃性的 所以判定为动态规划
2.这道题用到了johnson算法，我是拿个例子来理解的，
比如：假设再m1上的加工时间为a,在m2上的加工时间为b
如果作业i和作业j满足min(aj,bi) > min (ai,bj) 则称作业i和j
满足johnson法则

i在m1和m2上的加工时间为 3,4
j在m1和m2上的加工时间为 6,7
min(4,6) > min(3,7)
则作业i和j满足johnson法则

若先加工i
m2的结束时间 = 3+4+2+7 = 16
若先加工j
m2的结束时间 = 6+7+4 = 17

所以说johnson确定了加工的顺序

3.那么在处理数据的时候我们看到了一对一的摸样，但不能用map容器
因为数据当中有重复的部分，这时候我们完全可以用结构体数组来实现
同一个下标，但其可以含有多个值，java当中也可以创建一个对象来实现
但担心java 的虚拟机可能会超时。。。

4.本题中的johnson的算法的举例：



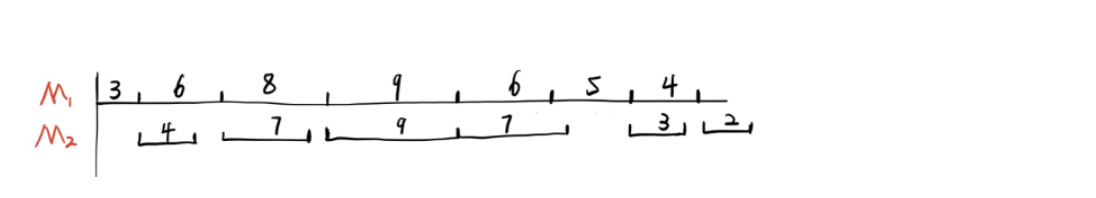
上面的例子是我理解时候看别人的例子，分享给大家

下面的例子：是本题的例子

三：上码

前言注释一下：1.这个题用完 Johnson的算法后，就基本上做完了，和前几道动态规划的题思路都不一样

这个当中的排序 用的是重写sort方法 利用结构体数组来处理数据（自认为本题唯一有成就感的地方）

/**
 	思路：
	1.判断动态规划：
	  首先m1的加工结束时间就是所有的时间和，但m2的加工时间和最小值，
	  求解过程是跳跃性的 所以判定为动态规划
	2.这道题用到了johnson算法，我是拿个例子来理解的，
	  比如：假设再m1上的加工时间为a,在m2上的加工时间为b
	 	  如果作业i和作业j满足min(aj,bi) > min (ai,bj) 则称作业i和j
		  满足johnson法则
		  
		   i在m1和m2上的加工时间为 3,4
		   j在m1和m2上的加工时间为 6,7
		   min(4,6) > min(3,7) 
		  则作业i和j满足johnson法则 
		  
		  若先加工i
		  m2的结束时间 = 3+4+2+7 = 16
		  若先加工j
		  m2的结束时间 = 6+7+4 = 17
		  
		  所以说johnson确定了加工的顺序
	
	3.那么在处理数据的时候我们看到了一对一的摸样，但不能用map容器
	  因为数据当中有重复的部分，这时候我们完全可以用结构体数组来实现
	  同一个下标，但其可以含有多个值，java当中也可以创建一个对象来实现
	  但担心java 的虚拟机可能会超时。。。  
*/ 

#include<bits/stdc++.h>
using namespace std;

struct Node{
	int number1; // 在m1上的加工时间
	int number2;//  在m2上的加工时间	
};

//N1集合当中ai的递增排序 
bool sort_N1(Node a,Node b){
	return a.number1 < b.number1;
} 

//N2中按bi的降序排序
bool sort_N2(Node a,Node b){
	return a.number2 > b.number2;
} 

int main(){
	
	int N;
	int a[101];
	int b[101];
	
	Node *stu1 = new Node[101];
	Node *stu2 = new Node[101]; 
	Node *stu3 = new Node[101]; 
	
	cin >> N; 
	
	for(int i = 0; i < N; i++){
		cin >> a[i] >> b[i];
	}
	
//	for(int i = 0; i < N; i++){
//		cout << b[i] << ' ';
//	}

	//开始处理数据在N1的集合当中是作业ai < bi(即在m2上的加工时间大于在m1上的加工时间)
	//N2上的集合是作业的(ai > bi) 
	//还要注意的是在N1上是按照ai的递增排序，在N2上是按照bi的递减排序
	
	int k1 = 0,k2 = 0;
	
	for(int i = 0; i < N; i++){
		//集合N1上 
		if(a[i] < b[i]){
			stu1[k1].number1 = a[i];
			stu1[k1].number2 = b[i];
			k1++;
		}else{
		//集合N2上	
			stu2[k2].number1 = a[i];
			stu2[k2].number2 = b[i];
			k2++;
		}
	}
	
//	for(int i = 0; i < k1; i++){
//		cout << stu1[i].number1 << ' ' << stu1[i].number2 << endl;
//	}	
	
	//对N1集合进行排序（按ai的递增排序） 
	sort(stu1,stu1+k1,sort_N1);
	
	//对N2集合进行排序（按bi的递减顺序进行排序）
	sort(stu2,stu2+k2,sort_N2); 
	
	//将N1和N2集合合并（N1在前，N2在后）
	int k3 = 0;
	for(int i = 0; i < k1; i++){
		 stu3[k3].number1 = stu1[i].number1;
		 stu3[k3].number2 = stu1[i].number2;
		 k3++;
	} 
	
	for(int i = 0; i < k2; i++){
		stu3[k3].number1 = stu2[i].number1;
		stu3[k3].number2 = stu2[i].number2;
		k3++; 
	}
	
	//验证数据 
//	for(int i = 0; i < k3; i++){
//		cout << stu3[i].number1 << ' ';
//	}

	//计算时间m1,m2的结束时间
	int m1,m2;
	m1 = stu3[0].number1;//第一个工作在m1执行完的时间
	m2 = stu3[0].number2 + m1;//第一个工作的总体执行时间
	
	for(int i = 1; i < N; i++){
		m1 = m1 + stu3[i].number1;//第i个工作在m1上的执行时间
		
		if(m1 < m2){//说明m2上的工作还没有完成 
			m2 = m2 + stu3[i].number2;//工作累积 
		}else if(m1 > m2){//说明m2需要等待，因为m1上的工作还未完成 
			m2 = m1 + stu3[i].number2; 
		} 
		 
	} 
	
	cout << m1 << ' ' << m2; 
	
	
} 



//20 30 50 120 90 110
//60 80 90 100 30 10

加油boy!! 睡觉了宝贝哈哈哈哈哈哈哈哈哈哈哈！