【机器学习】2、梯度下降（下）（随机梯度下降+小批量梯度下降）

最新推荐文章于 2024-06-18 17:00:00 发布

Wing以一

最新推荐文章于 2024-06-18 17:00:00 发布

阅读量1.5k

点赞数 1

分类专栏：机器学习文章标签：机器学习人工智能深度学习

本文链接：https://blog.csdn.net/qq_49183286/article/details/127190676

版权

机器学习专栏收录该内容

8 篇文章 4 订阅

订阅专栏

写在开始：局部规律的损失函数平均来说是整体损失函数的一个良好的估计。

梯度下降（原始版也被称为BGD，批量梯度下降）过程中每一次参数移动都是基于整体规律（全部数据集对应的损失函数）来进行每一次参数迭代，故而其无法跳脱局部最小值点和鞍点陷阱。如果我们采用局部规律（部分数据的损失函数）来进行每一次参数迭代呢？

随机梯度下降（Stochastic Gradient Descent）：每次参数迭代都挑选一条数据来构建损失函数。

小批量梯度下降（Mini-batch Gradient Descent）：每次选择一个小批数据（训练数据集的子集）来进行迭代。

一、随机梯度下降（Stochastic Gradient Descent）

Step1：确定数据集和模型

Step2：设置初始参数

Step3：执行梯度下降计算

二、小批量梯度下降（Mini-batch Gradient Descent）

一、随机梯度下降（Stochastic Gradient Descent）

SGD只是将梯度下降的“每次带入全部数据进行计算”改成了“每次带入一条数据进行计算”，但实际上，这么做会极大程度影响参数每一次移动的方向，从而使得参数最终无法收敛至全域最优解，但同时这么一来却也使得参数迭代过程能够跨越局部最小值点。

最终参数会在最小值点附近来回跳动。

SGD的计算本质是借助局部规律（而不是整体规律）来更新参数，而局部规律不一致性能够让参数在移动过程中保持灵活的移动方向，并因此能够逃离局部最小值点或鞍点陷阱，但方向不一致的代价是最终无法收敛到一个稳定的点，要改进这一问题则需要借助额外优化手段。

举个栗子：

Step1：确定数据集和模型

创建扰动项不大、基本满足 $y=2x_{1}-x_{2}+1$ 规律的数据集。

#设置随机数种子
np.random.seed(24)
#设置扰动项取值为0.01
features,labels=arrayGenReg(delta=0.01)

Step2：设置初始参数

#设置初始参数
np.random.seed(24)
w=np.random.randn(3,1)

# 计算w取值时SSE
SSELoss(features, w, labels)
# 计算w取值时MSE
MSELoss(features, w, labels)

Step3：执行梯度下降计算

w = sgd_cal(features, w, labels, lr_gd, epoch=40, lr=0.02)
print(w)

补充参数更新函数

def lr_gd(X, w, y):
    """
    线性回归梯度计算公式
    """
    m = X.shape[0]
    grad = 2 * X.T.dot((X.dot(w) - y)) / m      #MSE
    return grad

def w_cal(X, w, y, gd_cal, lr = 0.02, itera_times = 20):
    """
    梯度下降中参数更新函数
    :param X: 训练数据特征
    :param w: 初始参数取值
    :param y: 训练数据标签
    :param gd_cal：梯度计算公式
    :param lr: 学习率
    :param itera_times: 迭代次数
    :return w：最终参数计算结果
    """
    for i in range(itera_times):
        w -= lr * gd_cal(X, w, y)
    return w

def sgd_cal(X, w, y, gd_cal, epoch, lr = 0.02):
    """
    随机梯度下降计算函数
    :param X: 训练数据特征
    :param w: 初始参数取值
    :param y: 训练数据标签
    :param gd_cal：梯度计算公式
    :param epoch: 遍历数据集次数
    :param lr: 学习率
    :return w：最终参数计算结果
    """
    m = X.shape[0]
    n = X.shape[1]
    for j in range(epoch):
        for i in range(m):
            w = w_cal(X[i].reshape(1, n), w, y[i].reshape(1, 1), gd_cal=gd_cal, lr=lr, itera_times = 1)
    return w

二、小批量梯度下降（Mini-batch Gradient Descent）

先将训练数据进行“小批量”的切分，再按照随机梯度下降的算法进行计算。改进一下函数：

def sgd_cal(X, w, y, gd_cal, epoch,batch_size=1, lr = 0.02,shuffle=True,random_state=24):
    """
    随机梯度下降&小批量梯度下降计算函数
    :param X: 训练数据特征
    :param w: 初始参数取值
    :param y: 训练数据标签
    :param gd_cal：梯度计算公式
    :param epoch: 遍历数据集次数
    :batch_size: 每一个小批包含数据集的数量
    :param lr: 学习率
    :shuffle：是否在每个epoch开始前对数据集进行乱序处理
    :random_state：随机数种子值
    :return w：最终参数计算结果
    """
    m = X.shape[0]
    n = X.shape[1]
    batch_num=np.ceil(m/batch_size)
    X=np.copy(X)
    y=np.copy(y)
    for j in range(epoch):
        if shuffle:
            np.random.seed(random_state)
            np.random.shuffle(X)
            np.ramdom.seed(random_state)
            np.random.shuffle(y)
        for i in range(np.int(batch_num)):
            w = w_cal(X[i*batch_size: np.min([(i+1)*batch_size,m])], w,
                      y[i*batch_size: np.min([(i+1)*batch_size,m])], gd_cal=gd_cal, lr=lr, itera_times = 1)
    return w

小批量梯度下降也是借助不同批次数据的规律不一致性帮助参数跳出局部最小值陷阱，并且，由于规律不一致性，小批量梯度下降最终收敛结果也会呈现小幅震荡，只不过在所有的“随机不确定性”的方面，小批量梯度下降都比随机梯度下降显得更加稳健。

小批量梯度下降求解线性回归

数据集切分及参数设置

#设置随机数种子
np.random.seed(24)
#设置扰动项取值为0.01
features,labels=arrayGenReg(delta=0.01)

#数据集切分
Xtrain,Xtest,ytrain,ytest = array_split(features,labels,rate=0.7,random_state=24)

#设置初始参数
np.random.seed(24)
w=np.random.randn(3,1)

小批量梯度下降进行参数求解

w = sgd_cal(Xtrain, w, ytrain, lr_gd,batch_size=100, epoch=40, lr=0.02)
print(w)
print(MSELoss(Xtrain,w,ytrain))
print(MSELoss(Xtest,w,ytest))

观察迭代过程

np.random.seed(24)
w=np.random.randn(3,1)

trainLoss_l = []
testLoss_l = []

epoch=20

for i in range(epoch):
    w=sgd_cal(Xtrain,w,ytrain,lr_gd,batch_size=100,epoch=1,lr=0.02)
    trainLoss_l.append(MSELoss(Xtrain,w,ytrain))
    testLoss_l.append(MSELoss(Xtest,w,ytest))

plt.plot(list(range(epoch)),np.array(trainLoss_l).flatten(),label='train_l')
plt.plot(list(range(epoch)),np.array(testLoss_l).flatten(),label='teat_l')
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc=1)
plt.show()

局部规律的不一致性其实也将有助于提升模型收敛效率。小批量梯度下降不仅可以帮助损失函数跨越局部最小值点，同时也能加快梯度下降的收敛速度。

三、梯度下降算法的优化基础

收敛过程优化方法

1、数据归一化优化方法

通过构建一种样本空间之间的线性映射关系来进行数据数值的转化，这种转化并不会影响数据分布，即不会影响数据的内在规律，只是对数据的数值进行调整。

经典机器学习领域的数据归一化算法主要有两种，分别是0-1标准化（Max-Min Normalization）和Z-Score标准化。

（1) 0-1标准化（Max-Min Normalization）

过在输入特征中逐列遍历其中里的每一个数据，将Max和Min的记录下来，并通过Max-Min作为基数（即Min=0，Max=1）进行数据的归一化处理，基本公式为：

${x}_{normalization}=\frac{x-Min}{Max-Min}$

计算过程中逐列处理，用每一列中的元素减去当前列中的最小值，再除以该列的极差。

a=np.arange(10).reshape(5,2)
print(a)
a.max(axis=0)
a.min(axis=0)
nor_01=(a-a.min(axis=0))/(a.max(axis=0)-a.min(axis=0))  #广播
print(nor_01)

由此可见我们将a的两列都缩放到了0-1区间内

可以将0-1标准化封装成一个函数

def maxmin_norm(X):
    '''
    max-min normalization标准化函数
    '''
    maxmin_range = X.max(axis=0)-X.min(axis=0)
    return(X-X.min(axis=0))/maxmin_range

(2) Z-Score标准化

Z-score标准化利用原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。同样是逐列进行操作，每一条数据都减去当前列的均值再除以当前列的标准差，在这种标准化操作下，如果原数据服从正态分布，处理之后的数据服从标准正态分布。Z-Score标准化计算公式如下：

${x}_{normalization}=\frac{x-\mu }{\sigma }$

Z-Score标准化并不会将数据放缩在0-1之间，而是均匀地分布在0的两侧。类似这种数据也被称为Zero-Centered Data，在深度学习领域有重要应用。（更加严谨的做法，是在分母项、也就是标准差上加上一个非常小的常数 $\mu$ ，从而使得分母恒大于0。）

封装起来

def z_score(X):
    """
    Z-Score标准化函数
    """
    return (X - X.mean(axis=0)) / X.std(axis=0)

(3) Sigmoid标准化

利用Sigmoid函数对数据集的每一列进行处理，由于Sigmoid函数特性，处理之后的数据也将被压缩到0-1之间。 (非线性标准化）

(4) Z-Score标准化与0-1标准化对比

生成Zero-Centered Data

由于Z-Score标准化生成数据的Zero-Centered特性，使得其在深度学习领域备受欢迎（是Batch Normalization的一种特殊情况）。而在机器学习领域对于标签同时存在正负值的回归类问题，使用Z-Score能够避免对标签进行归一化。

标准正态分布

如果原始数据满足正态分布，则经过Z-Score转化之后就能转化为标准正态分布，进而可以利用标准正态分布诸多统计性质。

保留极端值分布

如果在一列数据中有一个值远高（低）于其他值，经过Z-Score转化之后，还可以保留这个极端值的分布。

2、数据归一化的算法应用

（1）数据集避免量纲不一致的问题

当数据集中不同列的量纲不一致（有的列单位是cm，有的列单位是m）时，通过对每一列的0-1标准化处理，能够消除因为这种不一致而引发的算法学习偏差。

如果是划分训练集和测试集进行建模并且进行归一化操作，那么在遵循“在训练集上训练，在测试集上进行测试”的基本原则下，我们首先在训练集上进行数据归一化处理并记录各列的极值，然后当模型训练完成之后，再借助训练集各列的极值来对测试机数据进行归一化，再带入模型进行测试。

如果这个过程对标签也进行了归一化处理，则标签的归一化过程和特征归一化过程无异，唯一需要注意的是如果是对未知数据进行预测，即需要模型输出和真实采集到数据类似的结果，则需要在模型输出的归一化的标签基础上进行逆向归一化处理。

一般来说如果是Z-Score标准化，则无需对标签进行标准化处理。

（2）帮助某些算法模型更好的挖掘规律

在通用的模型中，线性模型和距离类模型是两类典型的会受到各列绝对数值大小影响的模型，例如线性回归、KNN、K-Means（一种无监督的聚类模型）等，并且逻辑回归在使用ECOC编码进行类别判别时也是利用距离来判别样本最终归属，此时，由于各列的绝对数值会影响模型学习的偏重，模型会更加侧重于学习那些数值比较大的列，而无法“均匀”的从各列中提取有效信息，因此有时会出现较差的模型结果。但有些模型却不受此影响，典型的如树模型。

仿射变换指的是样本空间平移（加减某个数）和放缩（乘除某个数）的变换。0-1标准化过程中，平移就是减去每一列最小值，放缩就是除以某一列的极差。

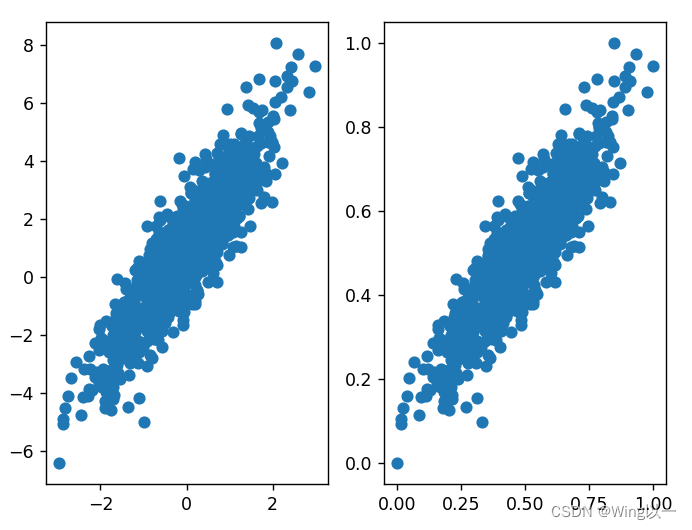
同一组数据我们发现归一化后并不影响数据的分布，改变的只是坐标轴的参数。

对于梯度下降算法来说，归一化能够提高收敛速度。在提高收敛速度方面，Z-Score效果要好于0-1标准化。

举个栗子感受一下收敛速度

# 创建数据及进行深拷贝
x = np.array([[1, 1], [3, 1]])
x_norm = np.copy(x)
#Z-Score标准化
x_norm[:, :1] = z_score(x_norm[:, :1])      #[:, :1]1前多一个:来保证归一化后的那一列还是二维的
print(x_norm)
y = np.array([[2], [4]])        ##Z-Score只对特征列进行归一化，标签列保留原始状态

归一化前的SSE损失函数为：

$SSE = (2-w-b)^2+(4-3w-b)$

而归一化之后的损失函数为：

$SSE = (2+w-b)^2 + (4-w-b)^2$

用两者梯度下降的等高线图来对比：

np.random.seed(24)
w = np.random.randn(2, 1)
w_norm = np.copy(w)

w, w_res = w_cal_rec(x, w, y, gd_cal = lr_gd, lr = 0.1, itera_times = 100)
w_norm, w_res_norm = w_cal_rec(x_norm, w_norm, y, gd_cal = lr_gd, lr = 0.1, itera_times = 100)

plt.subplot(121)
# 网格点坐标
x1, x2 = np.meshgrid(np.arange(1, 2, 0.001), np.arange(-1, 1, 0.001))
# 绘制等高线图
plt.contour(x1, x2, (2-x1-x2)**2+(4-3*x1-x2)**2)
# 参数点移动轨迹图
plt.plot(np.array(w_res)[:, 0], np.array(w_res)[:, 1], '-o', color='#ff7f0e')

plt.subplot(122)
# 网格点坐标
x1, x2 = np.meshgrid(np.arange(0, 4, 0.01), np.arange(-1, 3, 0.01))
# 绘制等高线图
plt.contour(x1, x2, (2+x1-x2)**2+(4-x1-x2)**2)
# 绘制参数点移动轨迹图
plt.plot(np.array(w_res_norm)[:, 0], np.array(w_res_norm)[:, 1], '-o', color='#ff7f0e')
plt.show()

梯度下降最快的一定是等高线的法线方向。（可以理解为未归一化之前的等高线图是椭圆形，而归一化后的等高线图偏向于正圆，正圆不同圈之间的法线一致或者说更相近）

附上正圆和椭圆对比更明显的图：

经过归一化的损失函数每次迭代效率都更高，因此相比其他损失函数，经过归一化的数据只需要更少次的迭代就能抵达最小值点，这也就是加快收敛速度的根本原因。

四、实例：用归一化对梯度下降算法进行优化

1、数据准备

读取待处理的数据

aba_data=pd.read_csv('D:\\abalone.txt',sep='\t',header=None)
print(aba_data)

aba_value=aba_data.values   #将原始数据集转换为二维数组
print(aba_value)
'''从原始数据集中抽取特征和标签'''
features=aba_value[:,1:3]
print(features)
labels=aba_value[:,4:5]
print(labels)

深拷贝数据用于归一化

features=np.concatenate((features,np.ones_like(labels)),axis=1)
#深拷贝features用于归一化
features_norm = np.copy(features)
#归一化处理
features_norm[:,:-1]=z_score(features_norm[:,:-1])
print(features,features_norm)

左图为原始特征值，右图为归一化后的特征值。

建模参数初始化

'''建模参数初始化'''
#设置初始参数
np.random.seed(24)      #随机数种子
n=features.shape[1]     #n为特征的列数
w=np.random.randn(n,1)

#记录迭代过程损失函数取值变化
Loss_l=[]
Loss_norm_l=[]

#迭代次数、遍历数据集次数
epoch=100

2、梯度下降算法

for i in range(epoch):
    w=w_cal(features,w,labels,lr_gd,lr=0.02,itera_times=1)
    Loss_l.append(MSELoss(features,w,labels))
    w_norm = w_cal(features_norm, w_norm, labels, lr_gd, lr=0.02, itera_times=1)
    Loss_norm_l.append(MSELoss(features_norm, w_norm, labels))

plt.plot(list(range(epoch)), np.array(Loss_l).flatten(), label='Loss_l')
plt.plot(list(range(epoch)), np.array(Loss_norm_l).flatten(), label='Loss_norm_l')
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc = 1)
plt.show()

经过归一化后的数据集，从损失函数变化图像上来看，收敛速度更快（损失函数下降速度更快），且最终收敛到一个更优的结果。

#用最小二乘法直接求解全域最优解
w1=np.linalg.lstsq(features,labels,rcond=-1)[0]
w2=np.linalg.lstsq(features_norm,labels,rcond=-1)[0]
#虽然归一化前后最小点值点位置不同，但对应于同一标签下的预测结果应该是一样的，并且全域最小值点对应MSE数值也应该一致。
print(features.dot(w1))
print(features_norm.dot(w2))
print(MSELoss(features_norm, w2, labels))
print(MSELoss(features, w1, labels))

在进行梯度下降计算过程中，在以0.02作为学习率进行迭代的过程中，两组模型都没有收敛到全域最小值点。（梯度下降过程中速度越来越慢，还没到达最小值点，梯度下降过程就趋向于“停止”的状态）

虽然学习率相同，但由于归一化之后最小值点附近梯度要更大（归一化后整个损失函数在不同区域对应梯度都更加均匀，从而在靠近最小值点附近的梯度也比归一化之前的损失函数梯度要大），因此同样的迭代次，在归一化之后的损失函数上参数点将移动至更加靠近最小值地附近的点。

五、学习率调度

目前一种最为通用的学习率调度方法是学习率衰减法，指的是在迭代开始时设置较大学习率，而伴随着迭代进行不断减小学习率。

对比恒定学习率和学习率衰减的两个梯度下降过程，并且都采用归一化后的数据集进行计算。

# 设置初始参数
np.random.seed(24) 
n = features.shape[1]
w = np.random.randn(n, 1)
w_lr = np.copy(w)

# 记录迭代过程损失函数取值变化
Loss_l = []
Loss_lr_l = []

# 迭代次数/遍历数据集次数
epoch = 20

for i in range(epoch):
    w = w_cal(features_norm, w, labels, lr_gd, lr = 0.2, itera_times = 10)
    Loss_l.append(MSELoss(features_norm, w, labels))
    w_lr = w_cal(features_norm, w_lr, labels, lr_gd, lr = 0.5*lr_lambda(i), itera_times = 10)
    Loss_lr_l.append(MSELoss(features_norm, w_lr, labels))

plt.plot(list(range(epoch)), np.array(Loss_l).flatten(), label='Loss_l')
plt.plot(list(range(epoch)), np.array(Loss_lr_l).flatten(), label='Loss_lr_l')
plt.xlabel('epochs')
plt.ylabel('MSE')
plt.legend(loc = 1)
plt.show()