初等数论及其应用 —— 笔记
符号表
mod \operatorname{mod} mod —— 模
( a , b ) (a,b) (a,b) —— a , b a,b a,b 的最大公约数
[ a , b ] [a,b] [a,b] —— a , b a,b a,b 的最小公倍数
a ∣ b a \mid b a∣b —— a a a 整除 b b b
a ∤ b a \nmid b a∤b —— a a a 不整除 b b b
m o d \bf{mod} mod —— 计算机中的模运算
x ‾ \overline{x} x —— x x x 模 p p p 的逆
同余
定义:
设
m
∈
Z
m \in Z
m∈Z ,若
a
,
b
∈
Z
a,b \in Z
a,b∈Z,且
m
∣
(
a
−
b
)
m \mid (a-b)
m∣(a−b) ,则称
a
a
a 和
b
b
b 模
m
m
m 同余
若 a a a 和 b b b 模 m m m 同余,记作 a ≡ b ( mod m ) a \equiv b \ (\operatorname{mod}\ m) a≡b (mod m)
若 m ∤ ( a − b ) m \nmid (a-b) m∤(a−b) ,记作 a ≢ b ( mod m ) a \not\equiv b \ (\operatorname{mod}\ m) a≡b (mod m),并称 a a a 模 m m m 不与 b b b 同余
整数 m m m 称为 同余的模
基础mod运算
(
i
)
(i)
(i) 自反性
a
≡
a
(
mod
m
)
a \equiv a \ (\operatorname{mod}\ m)
a≡a (mod m)
(
i
i
)
(ii)
(ii) 对称性
a
≡
b
(
mod
m
)
,
则
b
≡
a
(
mod
m
)
a \equiv b \ (\operatorname{mod}\ m),则 b \equiv a \ (\operatorname{mod}\ m)
a≡b (mod m),则b≡a (mod m)
(
i
i
i
)
(iii)
(iii) 传递性
a
≡
b
(
mod
m
)
,
b
≡
c
(
mod
m
)
,
则
a
≡
c
(
mod
m
)
a \equiv b \ (\operatorname{mod}\ m), b \equiv c \ (\operatorname{mod}\ m),则 a \equiv c \ (\operatorname{mod}\ m)
a≡b (mod m),b≡c (mod m),则a≡c (mod m)
模 m m m 的完全剩余系
定义:
一个模
m
m
m 完全剩余系是一个整数的集合,使得每个整数恰和此集合中的一个元素模
m
m
m 同余
特别的,其中由 0 , 1 , 2 , 3 , . . . , m − 1 0,1,2,3,...,m - 1 0,1,2,3,...,m−1 组成的集合被称为模 m m m 的最小非负剩余组成的完全剩余系
模运算
当 a ≡ b ( mod m ) a \equiv b\ (\operatorname{mod}\ m) a≡b (mod m) 时
( i ) (i) (i) a + c ≡ b + c ( mod m ) \ a + c \equiv b + c\ (\operatorname{mod}\ m) a+c≡b+c (mod m)
( i i ) (ii) (ii) a − c ≡ b − c ( mod m ) \ a - c \equiv b - c\ (\operatorname{mod}\ m) a−c≡b−c (mod m)
( i i i ) (iii) (iii) a c ≡ b c ( mod m ) \ ac \equiv bc\ (\operatorname{mod}\ m) ac≡bc (mod m)
( i i i i ) (iiii) (iiii) 若 m > 0 , d = ( c , m ) m > 0 , d = (c,m) m>0,d=(c,m) 且 a c ≡ b c ( mod m ) ac \equiv bc \ (\operatorname{mod}\ m) ac≡bc (mod m) ,则 a ≡ b ( mod m d ) a \equiv b \ (\operatorname{\operatorname{mod}}\ \frac{m}{d}) a≡b (mod dm)
推广至一般
当 a ≡ b ( mod m ) , c ≡ d ( mod m ) a \equiv b\ (\operatorname{mod}\ m),c \equiv d\ (\operatorname{mod}\ m) a≡b (mod m),c≡d (mod m) 时
( i ) (i) (i) a + c ≡ b + d ( mod m ) a + c \equiv b + d \ (\operatorname{mod}\ m) a+c≡b+d (mod m)
( i i ) (ii) (ii) a − c ≡ b − d ( mod m ) a - c \equiv b - d \ (\operatorname{mod}\ m) a−c≡b−d (mod m)
( i i i ) (iii) (iii) a c ≡ b d ( mod m ) ac \equiv bd \ (\operatorname{mod}\ m) ac≡bd (mod m)
引理 4.1 4.1 4.1
m m m 个 模 m m m 不同余的整数构成的集合是一个模 m m m 的完全剩余系
用鸽巢原理可证
定理 4.7 4.7 4.7
若 r 1 , r 2 , . . . , r m r_1,r_2,...,r_m r1,r2,...,rm 是 模 m m m 的 完全剩余系且正整数 a a a 满足 ( a , m ) = 1 (a,m) = 1 (a,m)=1,与任意整数 b b b 构成集合 { a r 1 + b , a r 2 + b , . . . , a r m + b } \{ar_1 + b,ar_2 + b,...,ar_m + b\} {ar1+b,ar2+b,...,arm+b} 仍是模 m m m 的完全剩余系
定理 4.8 4.8 4.8
若 a , b , k , m ∈ Z , k > 0 , m > 0 a,b,k,m \in Z , k > 0 , m > 0 a,b,k,m∈Z,k>0,m>0,且 a ≡ b ( mod m ) a \equiv b\ (\operatorname{mod}\ m) a≡b (mod m),则 a k ≡ b k ( mod m ) a ^ k \equiv b ^ k\ (\operatorname{mod}\ m) ak≡bk (mod m)
证明:
因为
a
≡
b
(
mod
m
)
a \equiv b \ (\operatorname{mod}\ m)
a≡b (mod m)
则 m ∣ ( a − b ) m \mid (a - b) m∣(a−b)
又因为 a k − b k = ( a − b ) ∑ i = 0 k − 1 a k − 1 − i b i a^k - b ^ k = (a - b)\sum_{i = 0}^{k - 1}a^{k - 1 - i}b^i ak−bk=(a−b)∑i=0k−1ak−1−ibi
所以 m ∣ ( a k − b k ) m \mid (a^k - b^k) m∣(ak−bk)
故 a k ≡ b k ( mod m ) a ^ k \equiv b ^ k \ (\operatorname{mod}\ m) ak≡bk (mod m)
定理 4.9 4.9 4.9
若 a ≡ b ( mod m 1 ) , a ≡ b ( mod m 2 ) , . . . , a ≡ b ( mod m k ) a \equiv b\ (\operatorname{mod}\ m_1),a \equiv b\ (\operatorname{mod}\ m_2),...,a \equiv b\ (\operatorname{mod}\ m_k) a≡b (mod m1),a≡b (mod m2),...,a≡b (mod mk)
则 a ≡ b ( mod [ m 1 , m 2 , . . . , m k ] ) a \equiv b\ (\operatorname{mod}\ [m_1,m_2,...,m_k]) a≡b (mod [m1,m2,...,mk])
推论
4.9.1
4.9.1
4.9.1
若在此基础上,
m
1
,
m
2
,
.
.
.
,
m
k
m_1,m_2,...,m_k
m1,m2,...,mk 两两互质
则 a ≡ b ( mod m 1 m 2 . . . m k ) a \equiv b\ (\operatorname{mod}\ m_1m_2...m_k) a≡b (mod m1m2...mk)
线性同余方程
设
x
x
x 为未知整数,求解一元同余方程
a
x
≡
b
(
mod
m
)
ax \equiv b\ (\operatorname{mod}\ m)
ax≡b (mod m)
定理 4.11 4.11 4.11
设 a , b , m ∈ Z , m > 0 , ( a , m ) = d a,b,m \in Z,m > 0\ ,\ \ (a,m) = d a,b,m∈Z,m>0 , (a,m)=d
若 d ∤ b d \nmid b d∤b,则 a x ≡ b ( mod m ) ax \equiv b\ (\operatorname{mod}\ m) ax≡b (mod m) 无解
若 d ∣ b d \mid b d∣b,则 a x ≡ b ( mod m ) ax \equiv b\ (\operatorname{mod}\ m) ax≡b (mod m) 恰有 d d d 个模 m m m 不同余的解
推论 4.11.1 4.11.1 4.11.1
若整数 a a a 和 m ( m > 0 ) m\ (m > 0) m (m>0) 互素 且 b ∈ Z b \in Z b∈Z
则 a x ≡ b ( mod m ) ax \equiv b\ (\operatorname{mod}\ m) ax≡b (mod m) 有唯一解
模的逆
定义:
对于
a
x
≡
1
(
mod
m
)
ax\equiv 1\ (\operatorname{mod}\ m)
ax≡1 (mod m) 的一个解称为
a
a
a 模
m
m
m 的逆
定理 4.12 4.12 4.12
设 p ∈ P , a ( a ∈ N ∗ ) p \in P,a(a\in N^*) p∈P,a(a∈N∗) 是其自身的逆
当且仅当 $a \equiv 1\ (\operatorname{mod}\ p) $ 或 $a \equiv -1\ (\operatorname{mod}\ p) $
中国剩余定理
设
m
1
,
m
2
,
.
.
.
,
m
r
(
m
i
∈
N
∗
[
i
=
0
,
1
,
2
,
.
.
.
,
r
]
)
m_1,m_2,...,m_r (m_i \in N^* [i = 0,1,2,...,r])
m1,m2,...,mr(mi∈N∗[i=0,1,2,...,r]) 且两两互质
则
{
x
≡
a
1
(
mod
m
1
)
x
≡
a
2
(
mod
m
2
)
.
.
.
.
.
.
x
≡
a
r
(
mod
m
r
)
\begin{equation*} \begin{cases} x\equiv a_1\ (\operatorname{mod}\ m_1) \\ x\equiv a_2\ (\operatorname{mod}\ m_2) \\ ...... \\ x\equiv a_r\ (\operatorname{mod}\ m_r) \\ \end{cases} \end{equation*}
⎩
⎨
⎧x≡a1 (mod m1)x≡a2 (mod m2)......x≡ar (mod mr)
有模
M
=
∏
i
=
1
r
m
i
M = \prod_{i = 1}^{r} m_i
M=∏i=1rmi 的唯一解
证明:
首先,构造出一个联立解
令 M k = M m k M_k = \frac{M}{m_k} Mk=mkM
因为 j ≠ k j \not = k j=k 时, ( m k , m j ) = 1 (m_k,m_j) = 1 (mk,mj)=1
所以 ( m k , M k ) = 1 (m_k,M_k) = 1 (mk,Mk)=1
故存在 y k y_k yk,使得 M k y k ≡ 1 ( mod m k ) M_ky_k \equiv 1\ (\operatorname{mod}\ m_k) Mkyk≡1 (mod mk)
对于 x x x
x = a 1 M 1 y 1 + a 2 M 2 y 2 + . . . + a r M r y r x = a_1M_1y_1 + a_2M_2y_2+...+a_rM_ry_r x=a1M1y1+a2M2y2+...+arMryr
从而得到 x ≡ a k M k y k ≡ a k ( mod m k ) x \equiv a_kM_ky_k \equiv a_k\ (\operatorname{mod}\ m_k) x≡akMkyk≡ak (mod mk)
对于 j ≠ k j \not = k j=k,因为 m k ∣ M j m_k\mid M_j mk∣Mj
所以 M j ≡ 0 ( mod m k ) M_j \equiv 0\ (\operatorname{mod}\ m_k) Mj≡0 (mod mk)
特解即为 x x x
设
x
0
,
x
1
x_0,x_1
x0,x1 为 方程组的两个联立解
对于每个 k k k,都有 x 0 ≡ x 1 ≡ a k ( mod m k ) x_0 \equiv x_1 \equiv a_k\ (\operatorname{mod}\ m_k) x0≡x1≡ak (mod mk)
所以 m k ∣ ( x 0 − x 1 ) m_k \mid (x_0 - x_1) mk∣(x0−x1)
由定理 4.9 4.9 4.9
M
∣
(
x
0
−
x
1
)
,
即
x
0
≡
x
1
(
mod
M
)
M | (x_0 - x_1) , 即 x_0 \equiv x_1\ (\operatorname{mod}\ M)
M∣(x0−x1),即x0≡x1 (mod M)
所以,联立解模 M M M 唯一
Tip: 利用 中国剩余定理 可以快速求模特殊合数的一些场景
二进制中的特殊模性质
引理 4.2 4.2 4.2
若 a , b ∈ N ∗ a,b \in N^* a,b∈N∗,则 ( 2 a − 1 ) mod ( 2 b − 1 ) (2^a - 1)\ \textbf{mod}\ (2^b-1) (2a−1) mod (2b−1) 的 最小正剩余 为 ( 2 r − 1 ) (2^r - 1) (2r−1);
其中 r 为 a mod b a\ \textbf{mod} \ b a mod b 的最小正剩余
引理 4.3 4.3 4.3
若 a , b ∈ N ∗ a,b \in N^* a,b∈N∗,则 ( 2 a − 1 , 2 b − 1 ) = 2 ( a , b ) − 1 (2^a-1,2^b-1) = 2^{(a,b)} - 1 (2a−1,2b−1)=2(a,b)−1
定理 4.14 4.14 4.14
正整数 ( 2 a − 1 , 2 b − 1 ) = 1 (2^a-1,2^b-1) = 1 (2a−1,2b−1)=1 ,当且仅当 ( a , b ) = 1 (a,b) = 1 (a,b)=1
多项式同余方程
定义:
形如
f
(
x
)
≡
0
(
mod
m
)
f(x) \equiv 0\ (\operatorname{mod}\ m)
f(x)≡0 (mod m) 的方程
其中
f
(
x
)
f(x)
f(x) 是次数大于
1
1
1 的整系数多项式
例:
求解
2
x
3
+
7
x
−
4
≡
0
(
mod
200
)
2x^3 + 7x - 4 \equiv 0\ (\operatorname{mod}\ 200)
2x3+7x−4≡0 (mod 200)
由中国剩余定理
200
=
2
3
⋅
5
2
200 = 2^3 \cdot 5^2
200=23⋅52
{ 2 x 3 + 7 x − 4 ≡ 0 ( mod 8 ) 2 x 3 + 7 x − 4 ≡ 0 ( mod 25 ) \begin{equation*} \begin{cases} 2x^3 + 7x - 4 \equiv 0\ (\operatorname{mod}\ 8) \\ 2x^3 + 7x - 4 \equiv 0\ (\operatorname{mod}\ 25) \end{cases} \end{equation*} {2x3+7x−4≡0 (mod 8)2x3+7x−4≡0 (mod 25)
由后试探出
{
x
≡
4
(
mod
8
)
x
≡
16
(
mod
25
)
\begin{equation*} \begin{cases} x \equiv 4\ (\operatorname{mod}\ 8) \\ x \equiv 16\ (\operatorname{mod}\ 25) \end{cases} \end{equation*}
{x≡4 (mod 8)x≡16 (mod 25)
由中国剩余定理,合并得
x
≡
116
(
mod
200
)
x\equiv 116\ (\operatorname{mod}\ 200)
x≡116 (mod 200)
出现了一个问题:分解的数是质数的幂,可能依然非常大,遍历试探对于人来说还是不太行
我们迫切需要一个 一般方法
求解 f ( x ) ≡ 0 ( mod m ) f(x) \equiv 0\ (\operatorname{mod}\ m) f(x)≡0 (mod m) 的一般方法.
由算数基本定理, m = ∏ p i k i m = \prod p_i^{k_i} m=∏piki
故关键在于 f ( x ) ≡ 0 ( mod p k − 1 ) f(x) \equiv 0\ (\operatorname{mod}\ p^{k-1}) f(x)≡0 (mod pk−1) 走向 f ( x ) ≡ 0 ( mod p k ) f(x) \equiv 0\ (\operatorname{mod}\ p^k) f(x)≡0 (mod pk)
我们决定引入 导数
定义:
设
f
(
x
)
=
∑
i
=
0
n
a
i
x
i
−
1
(
a
i
∈
R
)
f(x) = \sum_{i = 0}^n a_ix^{i-1}\ (a_i\in R)
f(x)=∑i=0naixi−1 (ai∈R)
则 f ( x ) f(x) f(x) 的导数 f ′ ( x ) = ∑ i = 1 n i a i x i − 1 f^{\prime}(x) = \sum_{i = 1}^n ia_ix^{i-1} f′(x)=∑i=1niaixi−1
引理 4.4 4.4 4.4
若 f ( x ) , g ( x ) f(x),g(x) f(x),g(x) 为多项式
则
(
f
+
g
)
′
(
x
)
=
f
′
(
x
)
+
g
′
(
x
)
(
c
f
)
′
(
x
)
=
c
(
f
′
(
x
)
)
(f + g)^{\prime}(x) = f^{\prime}(x) + g^{\prime}(x) \\ (cf)^{\prime}(x) = c(f^{\prime}(x))
(f+g)′(x)=f′(x)+g′(x)(cf)′(x)=c(f′(x))
引理 4.5 4.5 4.5
若 m , k ∈ N ∗ m,k\in N^* m,k∈N∗ 且 f ( x ) = x m f(x) = x ^ m f(x)=xm
则 f ( k ) ( x ) = [ ∏ i = 0 k − 1 ( m − i ) ] x m − k f^{(k)}(x) = [\prod_{i = 0}^{k-1}(m - i)] x^{m - k} f(k)(x)=[∏i=0k−1(m−i)]xm−k
于是乎 亨泽尔定理 横空出世
定理 4.15 4.15 4.15 (亨泽尔定理)
设 f ( x ) f(x) f(x) 是 整系数多项式, k ∈ N ∗ k\in N^* k∈N∗ 且 k ≥ 2 k \geq 2 k≥2, p ∈ P p \in P p∈P
进一步假设 r r r 是 f ( x ) ≡ 0 ( mod p k − 1 ) f(x) \equiv 0\ (\operatorname{mod}\ p^{k-1}) f(x)≡0 (mod pk−1) 的解
( i ) (i) (i) 若 f ′ ( r ) ≢ 0 ( mod p k − 1 ) f^{\prime}(r) \not\equiv 0\ (\operatorname{mod}\ p^{k-1}) f′(r)≡0 (mod pk−1)
则存在唯一 t ( t ∈ Z ) , 0 ≤ t ≤ p t\ (t\in Z),0 \leq t \leq p t (t∈Z),0≤t≤p
使得 f ( r + t p k − 1 ) ≡ 0 ( mod p k ) f(r + tp^{k-1}) \equiv 0\ (\operatorname{mod}\ p^k) f(r+tpk−1)≡0 (mod pk)
t \large t t 由 t ≡ − f ′ ( r ) ‾ f ( r ) p k − 1 ( mod p ) \large t \equiv - \overline{f^{\prime}(r)} \frac{f(r)}{p^{k-1}}\ (\operatorname{mod}\ p) t≡−f′(r)pk−1f(r) (mod p) 得出
( i i ) (ii) (ii) 若 f ′ ( r ) ≡ 0 ( mod p ) , f ( r ) ≡ 0 ( mod p k ) f^{\prime}(r) \equiv 0\ (\operatorname{mod}\ p),f(r) \equiv 0 (\operatorname{mod}\ p^k) f′(r)≡0 (mod p),f(r)≡0(mod pk)
则对 t ( t ∈ Z ) t\ (t\in Z) t (t∈Z) 都有 f ( r + t p k − 1 ) ≡ 0 ( mod p k ) f(r + tp^{k-1}) \equiv 0\ (\operatorname{mod}\ p^k) f(r+tpk−1)≡0 (mod pk)
( i i i ) (iii) (iii) 若 f ′ ( r ) ≡ 0 ( mod p ) , f ( r ) ≢ 0 ( mod p k ) f^{\prime}(r) \equiv 0\ (\operatorname{mod}\ p),f(r) \not\equiv 0 (\operatorname{mod}\ p^k) f′(r)≡0 (mod p),f(r)≡0(mod pk)
则 f ( x ) ≡ 0 ( mod p k ) f(x) \equiv 0\ (\operatorname{mod}\ p^k) f(x)≡0 (mod pk) 不存在解使得 x ≡ r ( mod p k − 1 ) x\equiv r\ (\operatorname{mod}\ p^{k-1}) x≡r (mod pk−1)
为了证明 亨泽尔定理,引入 T a y l o r Taylor Taylor 展开
引理 4.6 4.6 4.6
若 f ( x ) f(x) f(x) 是 n n n 次多项式; a , b ∈ R a,b \in R a,b∈R
则 f ( a + b ) = f ( a ) + f ′ ( a ) b + f ′ ′ ( a ) b 2 2 ! + . . . + f ( n ) ( a ) b n n ! \large f(a + b) = f(a) + f^{\prime}(a)b + \frac{f^{\prime\prime}(a)b^2}{2!} + ... + \frac{f^{(n)}(a)b^n}{n!} f(a+b)=f(a)+f′(a)b+2!f′′(a)b2+...+n!f(n)(a)bn
其中对于每一个
a
a
a,系数是关于
a
a
a 的整系数多项式
证明:
每个
n
n
n 次多项式
f
(
x
)
f(x)
f(x) 都是
x
m
x ^ m
xm 的倍数的和
其 m ≤ n m \leq n m≤n
由引理 4.4 4.4 4.4,仅对多项式 f ( x ) = x m f(x) = x ^ m f(x)=xm 建立引理 4.6 4.6 4.6
其中 m ∈ N ∗ m \in N^* m∈N∗
由二项式定理
(
a
+
b
)
m
=
∑
j
=
0
m
(
m
j
)
a
m
−
j
b
j
(a + b)^m = \sum_{j = 0}^m\dbinom{m}{j}a^{m - j}b^j
(a+b)m=j=0∑m(jm)am−jbj
由引理
4.5
4.5
4.5 知
f
m
(
j
)
(
a
)
=
∏
i
=
0
j
−
1
(
m
−
i
)
a
m
−
j
f^{(j)}_{m}(a) = \prod^{j-1}_{i = 0}(m-i)a^{m - j}
fm(j)(a)=i=0∏j−1(m−i)am−j
因此
f
m
(
j
)
(
a
)
j
!
=
(
m
j
)
a
m
−
j
\frac{f^{(j)}_m(a)}{j!} = \dbinom{m}{j}a^{m-j}
j!fm(j)(a)=(jm)am−j
证毕!
正式开始对 亨德尔定理 的证明
若 r r r 是 f ( r ) ≡ 0 ( mod p k ) f(r) \equiv 0\ (\operatorname{mod}\ p^k) f(r)≡0 (mod pk) 的解
则 其也为 f ( r ) ≡ 0 ( mod p k − 1 ) f(r) \equiv 0\ (\operatorname{mod}\ p^{k-1}) f(r)≡0 (mod pk−1) 的解
因此 此命题 等于 r + t p k − 1 , t ∈ Z r + tp^{k-1},t \in Z r+tpk−1,t∈Z,一旦确定了 t t t 的条件,证明完成
由 引理
4.6
4.6
4.6
f
(
r
+
t
p
k
−
1
)
=
∑
i
=
0
n
f
(
i
)
(
r
)
i
!
(
t
p
k
−
1
)
i
f(r + tp^{k-1}) = \sum_{i = 0}^{n}\frac{f^{(i)}(r)}{i!}(tp^{k-1})^i
f(r+tpk−1)=i=0∑ni!f(i)(r)(tpk−1)i
其中 f ( k ) ( r ) k ! ∈ Z , k = 1 , 2 , 3 , . . . , n . \frac{f^{(k)}(r)}{k!} \in Z,k = 1,2,3,...,n. k!f(k)(r)∈Z,k=1,2,3,...,n.
给定 k ≥ 2 k \geq 2 k≥2,对于 2 ≤ m ≤ n 2 \leq m \leq n 2≤m≤n,有 k ≤ m ( k − 1 ) k \leq m(k-1) k≤m(k−1) 且 p k ∣ p m ( k − 1 ) p^k \mid p^{m(k-1)} pk∣pm(k−1)
因此
f
(
r
+
t
p
k
−
1
)
≡
f
(
r
)
+
f
′
(
r
)
t
p
k
−
1
(
mod
p
k
)
f(r + tp^{k-1}) \equiv f(r) + f^{\prime}(r)tp^{k-1}\ (\operatorname{mod}\ p ^ k)
f(r+tpk−1)≡f(r)+f′(r)tpk−1 (mod pk)
因为 r + t p k − 1 r + tp^{k-1} r+tpk−1 是 f ( r + t p k − 1 ) ≡ 0 ( mod p k − 1 ) f(r + tp^{k-1}) \equiv 0\ (\operatorname{mod}\ p^{k-1}) f(r+tpk−1)≡0 (mod pk−1) 的一个解
所以
f
′
(
r
)
t
p
k
−
1
≡
−
f
(
r
)
(
mod
p
k
)
f^{\prime}(r)tp^{k-1} \equiv -f(r)\ (\operatorname{mod}\ p^k)
f′(r)tpk−1≡−f(r) (mod pk)
更进一步,由于 f ( r ) ≡ 0 ( mod p k − 1 ) f(r) \equiv 0\ (\operatorname{mod}\ p^{k-1}) f(r)≡0 (mod pk−1)
因此,两边同除 p k − 1 p^{k-1} pk−1
得到
f
′
(
r
)
t
≡
−
f
(
r
)
p
k
−
1
(
mod
p
)
f^{\prime}(r)t \equiv - \frac{f(r)}{p^{k-1}}\ (\operatorname{mod}\ p)
f′(r)t≡−pk−1f(r) (mod p)
通过考察其模 p p p 的解,即可证明 ( i ) , ( i i ) , ( i i i ) (i),(ii),(iii) (i),(ii),(iii)
情形 ( i ) (i) (i)
设 f ′ ( r ) ≢ 0 ( mod p ) f^{\prime}(r) \not\equiv 0\ (\operatorname{mod}\ p) f′(r)≡0 (mod p),则 ( f ′ ( r ) , p ) = 1 (f^{\prime}(r),p) = 1 (f′(r),p)=1,应用 推论 4.11.1 4.11.1 4.11.1
可知
t
t
t 的线性同余方程有唯一解
t
≡
(
−
f
(
r
)
p
k
−
1
)
f
′
(
r
)
‾
(
mod
p
)
t \equiv (-\frac{f(r)}{p^{k-1}})\overline{f^{\prime}(r)}\ (\operatorname{mod}\ p)
t≡(−pk−1f(r))f′(r) (mod p)
情形 ( i ) (i) (i) 得证!
情形 ( i i ) (ii) (ii)
$f^{\prime}® \equiv 0\ (\operatorname{mod}\ p) $ 时,有 ( f ′ ( r ) , p ) = p (f^{\prime}(r),p) = p (f′(r),p)=p
若 p ∣ f ( r ) p k − 1 p\mid \frac{f(r)}{p^{k-1}} p∣pk−1f(r) (此关系成立时当且仅当 f ( r ) ≡ 0 ( mod p k ) f(r)\equiv 0\ (\operatorname{mod}\ p^k) f(r)≡0 (mod pk)),则所有 t t t 都是解
这说明 x = r + t p k − 1 x = r + tp^{k-1} x=r+tpk−1 是解, t = 0 , 1 , . . . , p − 1 t = 0,1,...,p-1 t=0,1,...,p−1
情形 ( i i ) (ii) (ii) 得证!
情形 ( i i i ) (iii) (iii)
最后,考虑 f ′ ( r ) ≡ 0 ( mod p ) f^{\prime}(r) \equiv 0\ (\operatorname{mod}\ p) f′(r)≡0 (mod p),但 p ∤ f ( r ) p k − 1 p\nmid \frac{f(r)}{p^{k-1}} p∤pk−1f(r) 的情形
我们有 ( f ′ ( r ) , p ) = p (f^{\prime}(r),p) = p (f′(r),p)=p 且 f ( r ) ≡ 0 ( mod p k ) f(r) \equiv 0\ (\operatorname{mod}\ p^k) f(r)≡0 (mod pk)
所以 根据定理 4.11 4.11 4.11, t t t 的任意值均为解
情形 ( i i i ) (iii) (iii) 得证!
推论 4.15.1 4.15.1 4.15.1
假设 r r r 是 多项式同余方程 f ( x ) ≡ 0 ( mod p ) f(x) \equiv 0\ (\operatorname{mod}\ p) f(x)≡0 (mod p) 的一个解,且 p ∈ P p \in P p∈P
若 $ f^{\prime}® \not\equiv 0\ (\operatorname{mod}\ p) $,则存在模 p k p ^ k pk 的 唯一解 r k , k = 2 , 3 , . . . r_k,k = 2,3,... rk,k=2,3,...
使得 r 1 = r r_1 = r r1=r 且 r k = r k − 1 − f ( r k − 1 ) f ′ ( r ) ‾ r_k = r_{k-1} - f(r_{k-1})\overline{f^{\prime}(r)} rk=rk−1−f(rk−1)f′(r)
例题
1. 求解 f ( x ) = x 3 + x 2 + 2 x + 26 ≡ 0 ( mod 343 ) f(x) = x^3 + x ^ 2 + 2x + 26 \equiv 0\ (\operatorname{mod}\ 343) f(x)=x3+x2+2x+26≡0 (mod 343)
解: 因为 343 = 7 3 343 = 7^3 343=73
1 ◯ \textcircled{1} 1◯ 通过试探,可得
x 3 + x 2 + 2 x + 26 ≡ 0 ( mod 7 ) x^3 + x^2 + 2x + 26 \equiv 0\ (\operatorname{mod}\ 7) x3+x2+2x+26≡0 (mod 7)
的解 是 x ≡ 2 ( mod 7 ) x \equiv 2\ (\operatorname{mod}\ 7) x≡2 (mod 7)
2 ◯ \textcircled{2} 2◯ 因为 f ′ ( x ) = 3 x 2 + 2 x + 2 f^{\prime}(x) = 3x^2 + 2x + 2 f′(x)=3x2+2x+2
所以 f ′ ( 2 ) = 18 ≢ 0 ( mod 7 ) → f^{\prime}(2) = 18 \not \equiv 0\ (\operatorname{mod}\ 7) \rightarrow f′(2)=18≡0 (mod 7)→ 有唯一解
3 ◯ \textcircled{3} 3◯ 使用推论 4.15.1 4.15.1 4.15.1注意到 f ′ ( 2 ) ‾ = 4 ‾ ≡ 2 ( mod 7 ) \overline{f^{\prime}(2)} = \overline{4} \equiv 2\ (\operatorname{mod}\ 7) f′(2)=4≡2 (mod 7)
可得
r 2 = 2 − f ( 2 ) f ′ ( 2 ) ‾ = 2 − 42 ⋅ 2 = − 82 ≡ 16 ( mod 49 ) r 3 = 16 − f ( 16 ) f ′ ( 2 ) ‾ = 16 − 4410 ⋅ 2 = − 8804 ≡ 117 ( mod 343 ) r_2 = 2 - f(2) \overline{f^{\prime}(2)} = 2 - 42 \cdot 2 = -82\equiv 16\ (\operatorname{mod}\ 49) \\ r_3 = 16 - f(16)\overline{f^{\prime}(2)} = 16 - 4410 \cdot 2 = -8804 \equiv 117\ (\operatorname{mod}\ 343) r2=2−f(2)f′(2)=2−42⋅2=−82≡16 (mod 49)r3=16−f(16)f′(2)=16−4410⋅2=−8804≡117 (mod 343)得到 f ( x ) f(x) f(x) 模 343 343 343 的解为 x ≡ 114 ( mod 343 ) x \equiv 114\ (\operatorname{mod}\ 343) x≡114 (mod 343)
2.求解 x 2 + x + 7 ≡ 0 ( mod 27 ) x^2 + x + 7 \equiv 0 \ (\operatorname{mod}\ 27) x2+x+7≡0 (mod 27)
解:
设 f ( x ) = x 2 + x + 7 f(x) = x ^ 2 + x + 7 f(x)=x2+x+7,试探出 f ( x ) ≡ 0 ( mod 3 ) f(x) \equiv 0\ (\operatorname{mod}\ 3) f(x)≡0 (mod 3) 的解为 x ≡ 1 ( mod 3 ) x \equiv 1\ (\operatorname{mod}\ 3) x≡1 (mod 3)
由 f ′ ( x ) = 2 x + 1 f^{\prime}(x) = 2x + 1 f′(x)=2x+1,可知 $f^{\prime}(1) = 3 \equiv 0\ (\operatorname{mod}\ 3) $
且 因为 $f(1) = 9 \equiv 0\ (\operatorname{mod}\ 9) $
所以由 ( i i ) (ii) (ii) 得,对于 t ∈ Z t \in Z t∈Z , 1 + 3 t 1 + 3t 1+3t 都是模 9 9 9 的解
因为 $f(1) = 9 \not \equiv 0\ (\operatorname{mod}\ 27) $,由 ( i i i ) (iii) (iii),故不存在 原式 ≡ 0 ( mod 27 ) 原式 \equiv 0\ (\operatorname{mod}\ 27) 原式≡0 (mod 27)中 x ≡ 1 ( mod 9 ) x \equiv 1\ (\operatorname{mod}\ 9) x≡1 (mod 9) 的解
因为 f ( 4 ) = 27 ≡ 0 ( mod 27 ) f(4) = 27 \equiv 0\ (\operatorname{mod}\ 27) f(4)=27≡0 (mod 27),由 ( i i ) (ii) (ii) ,对于 t ∈ Z t \in Z t∈Z, 4 + 9 t 4 + 9t 4+9t 都是解
最后,因 $f(7) = 63 \not \equiv 0\ (\operatorname{mod}\ 27) $,由 ( i i i ) (iii) (iii),无解
综上, f ( x ) ≡ 0 ( mod 27 ) f(x) \equiv 0\ (\operatorname{mod}\ 27) f(x)≡0 (mod 27) 的解是 x ≡ 4 , 13 , 22 ( mod 27 ) x \equiv 4,13,22\ (\operatorname{mod}\ 27) x≡4,13,22 (mod 27)
利用波拉德 ρ \rho ρ 方法分解整数
设 n n n 是一个大合数, p p p 是它的最小素因子,我们的目标是选取整数 x 0 , x 1 , … , x s x_0,x_1,\ldots,x_s x0,x1,…,xs 使得它们有不同的模 n n n 最小非负剩余,但它们模 p p p 的最小非负剩余不是全部不同的,使用一些概率公式(书上没有详写)易证:
在
s
s
s 与
p
\sqrt{p}
p 相比较大,而与
n
\sqrt{n}
n 相比小且数字
x
1
,
x
2
,
…
x
s
x_1,x_2,\ldots x_s
x1,x2,…xs 是随机选取时,这是有可能发生的
一旦找到
x
i
x_i
xi 和
x
j
x_j
xj,
0
≤
i
≤
j
≤
s
0\leq i \leq j \leq s
0≤i≤j≤s,满足
x
i
≡
x
j
(
mod
p
)
x_i \equiv x_j (\operatorname{mod}\ p)
xi≡xj(mod p) 但
x
i
≢
x
j
(
mod
n
)
x_i \not \equiv x_j(\operatorname{mod}\ n)
xi≡xj(mod n),则
(
x
i
−
x
j
,
n
)
(x_i - x_j,n)
(xi−xj,n) 是
n
n
n 的非平凡因子
这是因为
p
p
p 整除
(
x
i
,
x
j
)
(x_i,x_j)
(xi,xj),但
n
n
n 不整除
(
x
i
−
x
j
)
(x_i - x_j)
(xi−xj),可以欧几里得算法迅速求出
(
x
i
−
x
j
,
n
)
(x_i - x_j,n)
(xi−xj,n),然而,对每对
(
i
,
j
)
,
0
≤
i
<
j
≤
s
(i,j),0\leq i < j \leq s
(i,j),0≤i<j≤s,求
(
x
i
−
x
j
,
n
)
(x_i - x_j,n)
(xi−xj,n) 共需要求
O
(
s
2
)
\mathcal{O}(s^2)
O(s2) 个最大公因子
我们将说明如何减少使用必须使用欧几里得算法的次数
我们用下面的方法寻找这样的整数
x
i
,
x
j
x_i,x_j
xi,xj :
首先,随机选取种子值
x
0
x_0
x0,而
f
(
x
)
f(x)
f(x) 次数大于
1
1
1 的整数系数多项式,然后用递归定义
x
k
+
1
≡
f
(
x
k
)
(
mod
n
)
,
0
≤
x
k
+
1
<
n
x_{k + 1} \equiv f(x_{k}) (\operatorname{mod}\ n),0 \leq x_{k + 1} < n
xk+1≡f(xk)(mod n),0≤xk+1<n
计算
x
k
x_k
xk,其中
k
=
1
,
2
,
…
k = 1,2,\ldots
k=1,2,…
多项式
f
(
x
)
f(x)
f(x) 的选取应该使得有很高的概率在出现重复之前生成适当多的整数
x
i
x_i
xi,
经验表明,多项式
f
(
x
)
=
x
2
+
1
f(x) = x ^ 2 + 1
f(x)=x2+1 在这一检验中表现良好
例题:
求
n
=
8051
n = 8051
n=8051 的非平凡因子
取种子 x 0 = 2 x_0 = 2 x0=2,生成多项式 f ( x ) = x 2 + 1 f(x) = x ^ 2 + 1 f(x)=x2+1
有 x 1 = 5 , x 2 = 26 , x 3 = 677 , x 4 = 7474 , x 5 = 2839 , x 6 = 871 x_1 = 5,x_2 = 26,x_3 = 677,x_4 = 7474,x_5 = 2839,x_6 = 871 x1=5,x2=26,x3=677,x4=7474,x5=2839,x6=871
由欧几里得算法
(
x
2
−
x
1
,
8051
)
=
(
21
,
8051
)
=
1
(
x
4
−
x
2
,
8051
)
=
(
7448
,
8051
)
=
1
\begin{align*} (x_2 - x_1,8051) & = (21,8051) &= 1 \\ (x_4 - x_2,8051) & = (7448,8051) &= 1 \end{align*}
(x2−x1,8051)(x4−x2,8051)=(21,8051)=(7448,8051)=1=1
因为
(
x
6
−
x
3
,
8051
)
=
(
194
,
8051
)
=
97
(x_6 - x_3,8051) = (194,8051) = 97
(x6−x3,8051)=(194,8051)=97
序列
x
i
x_i
xi 具有周期性质
其中
x
0
=
2
,
x
i
+
1
≡
x
i
2
+
1
(
mod
97
)
,
i
≥
1
,
x
1
=
5
x_0 = 2,x_{i + 1} \equiv x_i ^ 2 + 1 (\operatorname{mod}\ 97),i \geq 1,x_1 = 5
x0=2,xi+1≡xi2+1(mod 97),i≥1,x1=5
上图:
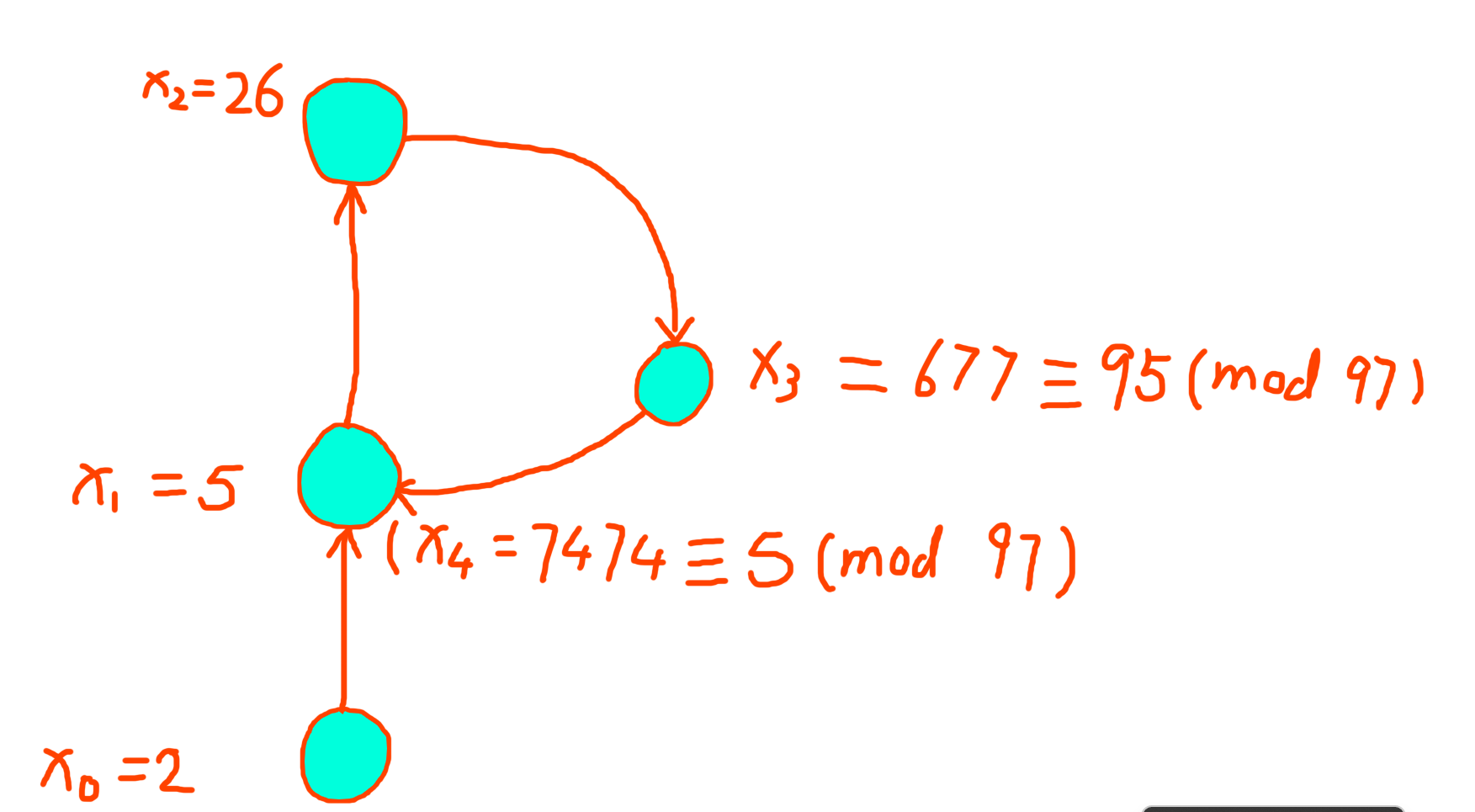
(神似 ρ \rho ρ,该方法因此得名)
ρ
\rho
ρ 的尾部是非周期部分(在周期出现之前)
事实证明:对具有相当大的素因子的分解中实用
在小素数试除和波拉德方法都失效时
才考虑真正的强力方法,如二次筛法或椭圆曲线法
特殊的同余式
定理 6.1 6.1 6.1(威尔逊定理)
若 p p p 是素数,则 ( p − 1 ) ! ≡ − 1 ( mod p ) (p - 1)! \equiv -1 (\operatorname{mod}\ p) (p−1)!≡−1(mod p)
证明:
当
p
=
2
p = 2
p=2 时,有
(
p
−
1
)
!
≡
1
≡
−
1
(
mod
2
)
(p - 1)! \equiv 1 \equiv -1 (\operatorname{mod}\ 2)
(p−1)!≡1≡−1(mod 2)
因此,当 p = 2 p = 2 p=2 时定理成立
现在,设 p p p 是大于 2 2 2 的素数
利用定理 4.11 4.11 4.11,对每个满足 1 ≤ a ≤ p − 1 1 \leq a \leq p - 1 1≤a≤p−1 的整数 a a a,存在一个逆 a a a,使得 1 ≤ a ‾ ≤ p − 1 1\leq \overline{a} \leq p - 1 1≤a≤p−1 且 a a ‾ ≡ 1 ( mod p ) a\overline{a}\equiv 1 (\operatorname{mod}\ p) aa≡1(mod p)
由定理 4.12 4.12 4.12 知,在小于 p p p 的正整数中,逆是其本身的数仅有 1 1 1 和 p − 1 p - 1 p−1 ,因此,可以将 2 2 2 到 ( p − 2 ) (p - 2) (p−2) 分成 p − 3 2 \frac{p - 3}{2} 2p−3 组
并且每组的乘积模
p
p
p 余
1
1
1,从而有
2
⋅
3
⋅
⋅
⋅
⋅
(
p
−
3
)
⋅
(
p
−
2
)
≡
1
(
mod
p
)
2 \cdot 3 \cdot \cdot \cdot \cdot (p - 3)\cdot (p - 2) \equiv 1 (\operatorname{mod}\ p)
2⋅3⋅⋅⋅⋅(p−3)⋅(p−2)≡1(mod p)
将同余式两边同时乘以
1
1
1 和
p
−
1
p - 1
p−1 得到
(
p
−
1
)
!
=
1
⋅
2
⋅
⋅
⋅
(
p
−
3
)
⋅
(
p
−
2
)
⋅
(
p
−
1
)
≡
1
⋅
(
p
−
1
)
≡
−
1
(
mod
p
)
(p - 1)! = 1 \cdot 2 \cdot \cdot \cdot (p - 3)\cdot (p - 2)\cdot(p - 1) \equiv 1 \cdot (p - 1) \equiv -1 (\operatorname{mod}\ p)
(p−1)!=1⋅2⋅⋅⋅(p−3)⋅(p−2)⋅(p−1)≡1⋅(p−1)≡−1(mod p)
得证!
定理 6.2 6.2 6.2 (威尔逊定理之逆定理)
设 n n n 为正整数且 n ≥ 2 n \geq 2 n≥2,若 ( n − 1 ) ! ≡ − 1 ( mod n ) (n - 1)! \equiv -1(\operatorname{mod}\ n) (n−1)!≡−1(mod n),则 n ∈ P n \in P n∈P
证明:
假设
n
n
n 是合数且
(
n
−
1
)
!
≡
−
1
(
mod
n
)
(n - 1)! \equiv -1(\operatorname{mod}\ n)
(n−1)!≡−1(mod n)
因 n n n 是合数,故有 n = a b n = ab n=ab,其中 1 < a < n , 1 < b < n , a ∈ Z , b ∈ Z 1 < a < n,1 < b < n,a \in Z,b \in Z 1<a<n,1<b<n,a∈Z,b∈Z
又因 a < n a < n a<n,且 a a a 是组成 ( n − 1 ) ! (n - 1)! (n−1)! 中的一个数
故 a ∣ ( n − 1 ) ! a | (n - 1)! a∣(n−1)!
因为 ( n − 1 ) ! ≡ − 1 ( mod n ) (n - 1)! \equiv -1 (\operatorname{mod}\ n) (n−1)!≡−1(mod n)
故 n ∣ [ ( n − 1 ) ! + 1 ] n | [(n-1)! + 1] n∣[(n−1)!+1]
由定理 1.8 1.8 1.8 (因为跳过了素数板块,所以会在下方给出)
这也意味着 a a a 也整除 ( n − 1 ) ! + 1 (n - 1)! + 1 (n−1)!+1
利用 定理 1.9 1.9 1.9(同上) 和 a ∣ ( n − 1 ) ! a | (n - 1)! a∣(n−1)! 且 a ∣ [ ( n − 1 ) ! + 1 ] a | [(n - 1) ! + 1] a∣[(n−1)!+1]
可知 a ∣ { [ ( n − 1 ) ! + 1 − ( n − 1 ) ! ] = 1 } a | \{[(n - 1) ! + 1 - (n - 1)!] = 1\} a∣{[(n−1)!+1−(n−1)!]=1}
这与 a > 1 a > 1 a>1 矛盾!
定理 1.8 1.8 1.8
如果 a , b , c ∈ Z a,b,c \in Z a,b,c∈Z 且 a ∣ b , b ∣ c a | b,b|c a∣b,b∣c 则 a ∣ c a | c a∣c
定理 1.9 1.9 1.9
如果 a , b , m , n ∈ Z a,b,m,n \in Z a,b,m,n∈Z 且 c ∣ a , c ∣ b c | a,c | b c∣a,c∣b 则 c ∣ ( m a + n b ) c | (ma + nb) c∣(ma+nb)
定理 6.3 6.3 6.3(费马小定理)
设 p ∈ P , a ∈ N ∗ p \in P,a \in N^{*} p∈P,a∈N∗ 且 p ∤ a p \nmid a p∤a,则 a p − 1 ≡ 1 ( mod p ) a^{p - 1} \equiv 1 (\operatorname{mod}\ p) ap−1≡1(mod p)
最经典的欧拉证法
证明:
考虑
p
−
1
p - 1
p−1 个整数,
a
,
2
a
,
3
a
,
4
a
,
…
,
(
p
−
1
)
a
a,2a,3a,4a,\ldots,(p - 1)a
a,2a,3a,4a,…,(p−1)a 它们都不能被
p
p
p 整除,
因为若 p ∣ j a p \mid ja p∣ja,那么因 p ∤ a p \nmid a p∤a,则由引理 3.4 3.4 3.4 知 p ∣ j p \mid j p∣j
因$ 1 \leq j \leq p - 1$,故不可能
进一步,在 a , 2 a , 3 a , … , ( p − 1 ) a a,2a,3a,\ldots,(p - 1)a a,2a,3a,…,(p−1)a 任意两个整数在模 p p p 下都不同余
为了证明这一点,我们假设 j a ≡ k a ( mod p ) ja \equiv ka (\operatorname{mod}\ p) ja≡ka(mod p)
其中 1 ≤ j < k ≤ p − 1 1 \leq j < k \leq p - 1 1≤j<k≤p−1
那么,根据 4.5.1 4.5.1 4.5.1,因 ( a , p ) = 1 (a,p) = 1 (a,p)=1,故 j ≡ k ( mod p ) j \equiv k (\operatorname{mod}\ p) j≡k(mod p)
这也是不可能的,因为
j
,
k
j,k
j,k 都是小于
p
p
p 的正整数
因为整数 a , 2 a , 3 a , … , ( p − 1 ) a a,2a,3a,\ldots,(p - 1)a a,2a,3a,…,(p−1)a 两两不同余,那么整数 a , 2 a , 3 a , … , ( p − 1 ) a a,2a,3a,\ldots,(p - 1)a a,2a,3a,…,(p−1)a 是 ( p − 1 ) (p - 1) (p−1) 个满足模 p p p 均不同余 0 0 0 且任何两个都互不同余的整数组成的集合中的元素
故由引理 4.1 4.1 4.1 可知, a , 2 a , … , ( p − 1 ) a a,2a,\ldots,(p - 1)a a,2a,…,(p−1)a 模 p p p 的最小正剩余按照一定的排列后必是 { 1 , 2 , 3 , … , p − 1 } \{1,2,3,\ldots,p-1\} {1,2,3,…,p−1}
由同余性
∏
i
=
1
p
−
1
(
i
a
)
≡
(
p
−
1
)
!
(
mod
p
)
\prod_{i = 1}^{p - 1} (ia) \equiv (p - 1)! (\operatorname{mod}\ p)
i=1∏p−1(ia)≡(p−1)!(mod p)
因此
a
p
−
1
(
p
−
1
)
!
≡
(
p
−
1
)
!
(
mod
p
)
a^{p - 1}(p - 1)! \equiv (p - 1)! (\operatorname{mod}\ p)
ap−1(p−1)!≡(p−1)!(mod p)
因为
(
p
−
1
)
!
(p - 1)!
(p−1)! 与
p
p
p 互质,利用推论
4.5.1
4.5.1
4.5.1,可找到一个
(
p
−
1
)
!
‾
\overline{(p - 1)!}
(p−1)! 消去
(
p
−
1
)
!
(p - 1)!
(p−1)! 得
a
p
−
1
≡
1
(
mod
p
)
a^{p - 1} \equiv 1(\operatorname{mod}\ p)
ap−1≡1(mod p)
欧拉定理
因为很重要,所以就单独拿出来讲
定义:设 n n n 是一个正整数,欧拉 ϕ \phi ϕ 函数 ϕ ( n ) \phi(n) ϕ(n) 定义为不超过 n n n 且与 n n n 互素的正整数的个数
定义:模 n n n 的即约剩余系是由 ϕ ( n ) \phi(n) ϕ(n) 个整数构成的集合,集合中每个元素均与 n n n 互素,且任何两个元素模 n n n 不同余
定理 6.13 6.13 6.13
设
r
1
,
r
2
,
…
,
r
ϕ
(
n
)
r_1,r_2,\ldots,r_{\phi(n)}
r1,r2,…,rϕ(n) 是模
n
n
n 的一个即约剩余系
若
a
a
a 是一个正整数且
(
a
,
n
)
=
1
(a,n) = 1
(a,n)=1,那么集合
a
r
1
,
a
r
2
,
…
,
a
r
ϕ
(
n
)
ar_1,ar_2,\ldots,ar_{\phi(n)}
ar1,ar2,…,arϕ(n) 也是模
n
n
n 的一个即约剩余系
证明:
1
◯
\textcircled{1}
1◯ 先证明每个整数
a
r
j
ar_j
arj 与
n
n
n 互素
假设 ( a r j , n ) > 1 (ar_j,n) > 1 (arj,n)>1,那么 ( a r j , n ) (ar_j,n) (arj,n) 有一个素因子 p p p
因此,或
p
∣
a
p\mid a
p∣a 或
p
∣
r
j
p \mid r_j
p∣rj,从而或
p
∣
a
p\mid a
p∣a 且
p
∣
n
p \mid n
p∣n,或
p
∣
r
j
p \mid r_j
p∣rj 且
p
∣
n
p \mid n
p∣n
(翻译成C++语言就是:if((a % p == 0 && n % p == 0) || (r[j] % p == 0 && n % p == 0)))
但因 r j r_j rj 是模 n n n 的即约剩余系中的元素,
故 p ∣ r j p\mid r_j p∣rj 和 p ∣ n p \mid n p∣n 不能同时成立
又因 ( a , n ) = 1 (a,n) = 1 (a,n)=1,故 p ∣ a p \mid a p∣a 和 p ∣ n p \mid n p∣n 不能同时成立,因此,对 j = 1 , 2 , 3 , … , ϕ ( n ) j = 1,2,3,\ldots,\phi(n) j=1,2,3,…,ϕ(n), a r j ar_j arj 与 n n n 互素
2 ◯ \textcircled{2} 2◯ 为了说明 a r j ar_j arj 模 n n n 彼此互不同余,设 a r j ≡ a r k ( mod n ) ar_j \equiv ar_k(\operatorname{mod}\ n) arj≡ark(mod n)
其中, j j j 和 k k k 是不同的正整数且 1 ≤ j , k ≤ ϕ ( n ) 1 \leq j,k \leq \phi(n) 1≤j,k≤ϕ(n)
因 ( a , n ) = 1 (a,n) = 1 (a,n)=1,由推论 4.5.1 4.5.1 4.5.1 知 r j ≡ r k ( mod n ) r_j \equiv r_k (\operatorname{mod}\ n) rj≡rk(mod n)
又因 r j r_j rj 和 r k r_k rk 是前一个模 n n n 的即约剩余系中的元素
故 r j ≢ r k ( mod n ) r_j \not \equiv r_k (\operatorname{mod}\ n) rj≡rk(mod n),矛盾!
定理 6.14 6.14 6.14(欧拉定理)
设 m m m 是一个正整数, a a a 是一个整数且 ( a , m ) = 1 (a,m) = 1 (a,m)=1,那么 a ϕ ( m ) ≡ 1 ( mod m ) a^{\phi(m)} \equiv 1 (\operatorname{mod}\ m) aϕ(m)≡1(mod m)
证明:
令
r
1
,
r
2
,
…
,
r
ϕ
(
m
)
r_1,r_2,\ldots,r_{\phi(m)}
r1,r2,…,rϕ(m) 是由不超过
m
m
m 且和
m
m
m 互素的元素组成的即约剩余系
由定理 6.13 6.13 6.13
因 ( a , m ) = 1 (a,m) = 1 (a,m)=1,故集合 a r 1 , a r 2 , … r ϕ ( m ) ar_1,ar_2,\ldots r_{\phi(m)} ar1,ar2,…rϕ(m) 也是模 m m m 的一个即约剩余系
从而,在一定顺序下 a r 1 , a r 2 , … , a r ϕ ( m ) ar_1,ar_2,\ldots,ar_{\phi(m)} ar1,ar2,…,arϕ(m) 的最小正剩余一定是 r 1 , r 2 , … , r ϕ ( m ) r_1,r_2,\ldots,r_{\phi(m)} r1,r2,…,rϕ(m)
因此, a r 1 a r 2 … , a r ϕ ( m ) ≡ r 1 r 2 r 3 … r ϕ ( m ) ( mod m ) ar_1ar_2\ldots,ar_{\phi(m)} \equiv r_1r_2r_3\ldots r_{\phi(m)} \ (\operatorname{mod}\ m) ar1ar2…,arϕ(m)≡r1r2r3…rϕ(m) (mod m)
因此, a ϕ ( m ) r 1 r 2 … r ϕ ( m ) ≡ r 1 r 2 … r ϕ ( m ) ( mod m ) a^{\phi(m)}r_1r_2\ldots r_{\phi(m)} \equiv r_1r_2\ldots r_{\phi(m)} (\operatorname{mod}\ m) aϕ(m)r1r2…rϕ(m)≡r1r2…rϕ(m)(mod m)
因为 ( r 1 r 2 r 3 … r ϕ ( m ) , m ) = 1 (r_1r_2r_3\ldots r_{\phi(m)},m) = 1 (r1r2r3…rϕ(m),m)=1
故由推论 4.5.1 4.5.1 4.5.1 知, a ϕ ( m ) ≡ 1 ( mod m ) a^{\phi(m)} \equiv 1(\operatorname{mod}\ m) aϕ(m)≡1(mod m)
乘性函数
定义:定义在所有正整数的函数称为算术函数
定义: 如果算术函数
f
f
f 对任意两个互素的正整数
n
n
n 和
m
m
m,均有 $f(mn) = f(m)f(n) $,就称为乘性函数(或积性函数)
如果对任意两个正整数
n
n
n 和
m
m
m,均有
f
(
m
n
)
=
f
(
m
)
f
(
n
)
f(mn) = f(m)f(n)
f(mn)=f(m)f(n),就称为完全乘性(或完全积性)函数
定理 7.1 7.1 7.1
如果 f f f 是一个乘性函数,且对任意正整数 n n n 有素幂因子分解 n = p 1 a 1 p 2 a 2 p 3 a 3 … p s a s n = p_1^{a_1}p_2^{a_2}p_3^{a_3}\ldots p_s^{a_s} n=p1a1p2a2p3a3…psas,那么 f ( n ) = f ( p 1 a 1 ) f ( p 2 a 2 ) f ( p 3 a 3 ) … f ( p s a s ) f(n) = f(p_1^{a_1})f(p_2^{a_2})f(p_3^{a_3})\ldots f(p_s^{a_s}) f(n)=f(p1a1)f(p2a2)f(p3a3)…f(psas)
回到 ϕ \phi ϕ 函数
定理 7.2 7.2 7.2
如果 p p p 是素数,则 $\phi§ = p - 1 $
反之,若 p p p 是正整数且满足 $\phi§ = p - 1 $,则 p p p 是素数
定理 7.3 7.3 7.3
设 p p p 是素数, a a a 是一个正整数,那么 $\phi(p^a) = p^a - p^{a - 1} $
证明:
不超过
p
a
p^a
pa 且和
p
p
p 不互素的正整数,即
k
p
kp
kp,其中
1
≤
k
≤
p
a
−
1
1 \leq k \leq p^{a - 1}
1≤k≤pa−1
因为恰有 p a − 1 p^{a - 1} pa−1 个这样的数,故存在 p a − p a − 1 p^a - p^{a - 1} pa−pa−1 个与 p a p^a pa 互素且不超过 p a p^a pa 的素因子,所以 ϕ ( p a ) = p a − p a − 1 \phi(p^a) = p^a - p^{a - 1} ϕ(pa)=pa−pa−1
定理 7.4 7.4 7.4 *
设 m m m 和 n n n 是互素的正整数,那么 $\phi(mn) = \phi(m)\phi(n) $
* 证明:
我们用下列的方式列出不超过
m
n
mn
mn 的所以正整数
1
m
+
1
…
(
n
−
1
)
m
+
1
2
m
+
2
…
(
n
−
1
)
m
+
2
⋮
⋮
⋮
r
m
+
r
…
(
n
−
1
)
m
+
r
⋮
⋮
⋮
m
2
m
…
n
m
\begin{matrix} 1 & m + 1 & \ldots & (n - 1)m + 1 \\ 2 & m + 2 & \ldots & (n - 1)m + 2 \\ \vdots & \vdots & & \vdots \\ r & m + r & \ldots & (n - 1)m + r \\ \vdots & \vdots & & \vdots \\ m & 2m & \ldots & nm \\ \end{matrix}
12⋮r⋮mm+1m+2⋮m+r⋮2m…………(n−1)m+1(n−1)m+2⋮(n−1)m+r⋮nm
现在假设 r r r 是不超过 m m m 的正整数
且设 ( m , r ) = d > 1 (m,r) = d > 1 (m,r)=d>1,那么第 r r r 行中没有与 m n mn mn 互素元素
因为该行每个元素 k m + r km + r km+r,其中 k k k 是整数,且满足 0 ≤ k ≤ n − 1 0 \leq k \leq n - 1 0≤k≤n−1
又因为 d ∣ m d\mid m d∣m 和 d ∣ r d \mid r d∣r,所以 d ∣ ( k m + r ) d \mid (km + r) d∣(km+r)
因此,为找到该表中所有 与 m n mn mn 互素的整数
只需要考虑满足 ( m , r ) = 1 (m,r) = 1 (m,r)=1 的第 r r r 行
如果 ( m , r ) = 1 (m,r) = 1 (m,r)=1 且 1 ≤ r ≤ m 1 \leq r \leq m 1≤r≤m,则必须确定该行中有多少元素与 m n mn mn 互素
该行中元素为 r , m + r , … , ( n − 1 ) m + r r,m + r,\ldots,(n - 1)m + r r,m+r,…,(n−1)m+r
因为, ( m , r ) = 1 (m,r) = 1 (m,r)=1,故其中每个元素都与 m n mn mn 互素
由定理 4.6 4.6 4.6 可知,第 r r r 行中 n n n 个整数形成模 n n n 的完全剩余系
所以恰好有 ϕ ( n ) \phi(n) ϕ(n) 个与 n n n 互素的整数
因为这 ϕ ( n ) \phi(n) ϕ(n) 个整数也与 m m m 互素,所以它们也是与 m n mn mn 互素的
因为 ϕ ( m ) \phi(m) ϕ(m) 行中每行恰有 ϕ ( n ) \phi(n) ϕ(n) 个与 m n mn mn 互素的整数
所以 $\phi(mn) = \phi(m)\phi(n) $
定理 7.5 7.5 7.5 *
设
n
=
p
1
a
1
p
2
a
2
…
p
k
a
k
n = p_1^{a_1}p_2^{a_2}\ldots p_{k}^{a_k}
n=p1a1p2a2…pkak 为 正整数
n
n
n 的素因子分解,那么
ϕ
(
n
)
=
n
(
1
−
1
p
1
)
(
1
−
1
p
2
)
…
(
1
p
k
)
\phi(n) = n(1 - \frac{1}{p_1})(1 - \frac{1}{p_2})\ldots(\frac{1}{p_k})
ϕ(n)=n(1−p11)(1−p21)…(pk1)
即:
ϕ
(
n
)
=
n
∏
i
=
1
k
(
1
−
1
p
i
)
\phi(n) = n\prod_{i = 1}^{k}(1 - \frac{1}{p_i})
ϕ(n)=ni=1∏k(1−pi1)
证明:
因为 定理
7.4
7.4
7.4,
ϕ
\phi
ϕ 是乘性函数,故由定理
7.1
7.1
7.1 可知
ϕ
(
n
)
=
ϕ
(
p
1
a
1
)
ϕ
(
p
2
a
2
)
…
ϕ
(
p
k
a
k
)
\phi(n) = \phi(p_1^{a_1})\phi(p_2^{a_2})\ldots\phi(p_k^{a_k})
ϕ(n)=ϕ(p1a1)ϕ(p2a2)…ϕ(pkak)
又由定理
7.3
7.3
7.3,当
j
=
1
,
2
,
…
,
n
j = 1,2,\ldots,n
j=1,2,…,n 时
ϕ
(
p
j
a
j
)
=
p
j
a
j
−
p
j
a
j
−
1
=
p
j
a
j
(
1
−
1
p
j
)
\phi(p_j^{a_j}) = p_j^{a_j} - p_j^{a_j - 1} = p_j^{a_j}(1 - \frac{1}{p_j})
ϕ(pjaj)=pjaj−pjaj−1=pjaj(1−pj1)
因此
ϕ
(
n
)
=
p
1
a
1
(
1
−
1
p
1
)
p
2
a
2
(
1
−
1
p
2
)
…
p
k
a
k
(
1
−
1
p
k
)
=
p
1
a
1
p
2
a
2
p
3
a
3
…
p
k
a
k
⋅
∏
i
=
1
k
(
1
−
1
p
i
)
=
n
∏
i
=
1
k
(
1
−
1
p
i
)
\begin{align*} \phi(n) &= p_1^{a_1}(1 - \frac{1}{p_1})p_2^{a_2}(1 - \frac{1}{p_2})\ldots p_k^{a_k}(1 - \frac{1}{p_k})\\ &= p_1^{a_1}p_2^{a_2}p_3^{a_3}\ldots p_k^{a_k}\cdot \prod_{i = 1}^k (1 - \frac{1}{p_i})\\ &= n \prod_{i = 1}^k (1 - \frac{1}{p_i}) \end{align*}
ϕ(n)=p1a1(1−p11)p2a2(1−p21)…pkak(1−pk1)=p1a1p2a2p3a3…pkak⋅i=1∏k(1−pi1)=ni=1∏k(1−pi1)
应用:
ϕ
(
100
)
=
ϕ
(
2
2
⋅
5
2
)
=
100
(
1
−
1
2
)
(
1
−
1
5
)
=
40
ϕ
(
720
)
=
ϕ
(
2
4
⋅
3
2
⋅
5
)
=
720
(
1
−
1
2
)
(
1
−
1
3
)
(
1
−
1
5
)
=
192
\begin{align} \phi(100) &= \phi(2^2\cdot 5^2) = 100 (1 - \frac{1}{2})(1 - \frac{1}{5}) = 40 \\ \phi(720) &= \phi(2^4\cdot 3^2 \cdot 5) = 720(1 - \frac{1}{2})(1 - \frac{1}{3})(1 - \frac{1}{5}) = 192 \\ \end{align}
ϕ(100)ϕ(720)=ϕ(22⋅52)=100(1−21)(1−51)=40=ϕ(24⋅32⋅5)=720(1−21)(1−31)(1−51)=192
定理 7.6 7.6 7.6
设 n n n 是一个大于 2 2 2 的正整数,那么 ϕ ( n ) \phi(n) ϕ(n) 是偶数
证明:
假设
n
=
p
1
a
1
p
2
a
2
…
p
k
a
k
n = p_1^{a_1}p_2^{a_2}\ldots p_{k}^{a_k}
n=p1a1p2a2…pkak 是
n
n
n 的素因子分解
因为 ϕ \phi ϕ 是乘性函数
所以 $\phi(n) = \prod_{i = 1}^{k} \phi(p_i^{a_i}) $
由定理
7.3
7.3
7.3
ϕ
(
p
i
a
i
)
=
p
i
a
i
−
1
(
p
i
−
1
)
\phi(p_i^{a_i}) = p_i^{a_i - 1}(p_i - 1)
ϕ(piai)=piai−1(pi−1)
当 p i p_i pi 为 奇素数时 p i − 1 p_i - 1 pi−1 是偶数
当 p i = 2 p_i = 2 pi=2 且 a i > 1 a_i > 1 ai>1 时 p i a i − 1 p_i^{a_i - 1} piai−1 为偶数
这两个条件在 { n > 2 且 n ∈ N ∗ } \{n > 2 且 n \in N^* \} {n>2且n∈N∗} 下至少满足一个
故 ϕ ( p i a i ) \phi(p_i^{a_i}) ϕ(piai) 在 1 ≤ i ≤ k 1 \leq i \leq k 1≤i≤k 时至少有一个偶数
因此 ϕ ( n ) \phi(n) ϕ(n) 是偶数
定义: 设
f
f
f 是一个算术函数,那么
F
(
n
)
=
∑
d
∣
n
f
(
d
)
F(n) = \sum_{d \mid n} f(d)
F(n)=d∣n∑f(d)
代表
f
f
f 在
n
n
n 的所有正因子处的值之和
函数
F
F
F 称为
f
f
f 的和函数
定理 7.7 7.7 7.7
设
n
n
n 是正整数,那么
∑
d
∣
n
ϕ
(
d
)
=
n
\sum_{d \mid n} \phi(d) = n
d∣n∑ϕ(d)=n
证明:
我们将
1
∼
n
1\sim n
1∼n 的整数构成的集合进行分类
整数 m m m 如果与 n n n 的最大公因子为 d d d
则 m m m 属于 C d C_d Cd 类
就是说,如果 m ∈ C d m \in C_d m∈Cd,那么 ( m , n ) = d (m,n) = d (m,n)=d
当且仅当 ( m d , n d ) = 1 (\frac{m}{d},\frac{n}{d}) = 1 (dm,dn)=1
所以, C d C_d Cd 类中所含整数的个数是所有不超过 n d \frac{n}{d} dn 且和整数 n d \frac{n}{d} dn 互素的正整数的个数
从上面的分析可以看到, C d C_d Cd 类中存在 ϕ ( n d ) \phi(\frac{n}{d}) ϕ(dn) 个整数
因为我们将 1 ∼ n 1\sim n 1∼n 的所有整数分成互不相交的类,且每个整数只属于其中 1 1 1 个类,所以这些不同的类所含的整数个数之和就是 n n n
因此,
n
=
∑
d
∣
n
ϕ
(
n
d
)
n = \sum_{d \mid n} \phi(\frac{n}{d})
n=d∣n∑ϕ(dn)
因为 d d d 取遍所有整除 n n n 的正整数, n d \frac{n}{d} dn 也取遍它的所有因子
所以
n
=
∑
d
∣
n
ϕ
(
n
d
)
=
∑
d
∣
n
ϕ
(
d
)
n = \sum_{d \mid n} \phi(\frac{n}{d}) = \sum_{d \mid n} \phi(d)
n=d∣n∑ϕ(dn)=d∣n∑ϕ(d)
设 k k k 是一个正整数,求满足 ϕ ( n ) = k \phi(n) = k ϕ(n)=k 的所有正整数 n n n 的解的一个有用的办法就是给出满足方程 ϕ ( n ) = ∏ i = 1 k p i a i − 1 ( p i − 1 ) \phi(n) = \prod_{i = 1}^k p_i^{a_i - 1}(p_i - 1) ϕ(n)=∏i=1kpiai−1(pi−1) 的所有正整数解 n n n,其中 n n n 的素因子分解为 n = ∏ i = 1 k p i a i n = \prod_{i = 1}^k p_i^{a_i} n=∏i=1kpiai
例:
求解 ϕ ( n ) = 8 \phi(n) = 8 ϕ(n)=8 的所有整数解解:
由题
a ∤ n ( a > 9 ) , 7 ∤ n a \nmid n(a > 9),7 \nmid n a∤n(a>9),7∤n
所以 n = 2 a 3 b 5 c ( a , b , c ∈ N ) n = 2^a3^b5^c(a,b,c \in N) n=2a3b5c(a,b,c∈N)
故 b = 0 , 1 b = 0,1 b=0,1 及 c = 0 , 1 c = 0,1 c=0,1
分讨 4 4 4 种情形
得 n = 15 , 16 , 20 , 24 , 30 n = 15,16,20,24,30 n=15,16,20,24,30






















 295
295

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








