2024/07/01
AtCoder Beginner Contest 360
E - Random Swaps of Balls
期望 d p dp dp 题
问题陈述
有 N − 1 N - 1 N−1 个白球和一个黑球。这些 N N N 个球排成一排,黑球最初位于最左边的位置。
高桥正好要进行下面的操作 K K K 次。
- 在 1 1 1 和 N N N 之间均匀随机地选择一个整数,包括两次。设 a a a 和 b b b 为所选整数。如果是 a ≠ b a \neq b a=b ,把左边的 a a a -th 和 b b b -th 两个球交换。
经过 K K K 次操作后,让黑球位于左边的 x x x -th 位置。求 x x x 的期望值,模为 998244353 998244353 998244353 。
模数 998244353 998244353 998244353 的期望值是多少?
可以证明所求的期望值总是有理数。此外,在本题的限制条件下,还可以证明如果用不可约分数 P Q \frac{P}{Q} QP 表示这个值,那么就是 Q ≢ 0 ( m o d 998244353 ) Q \not \equiv 0 \pmod{998244353} Q≡0(mod998244353) 。因此,存在一个唯一的整数 R R R ,使得 R × Q ≡ P ( m o d 998244353 ) , 0 ≤ R ≤ 998244353 R \times Q \equiv P \pmod{998244353}, 0 \leq R \leq 998244353 R×Q≡P(mod998244353),0≤R≤998244353 。报告这个 R R R .
参考了 Lanly 的题解
首先,我们可以看到:对于每一个不为 1 1 1 位置,其价值相等
那么,我们自然设置出状态:
- 其在 1 1 1 号位上
- 其不在 1 1 1 号位上
对于第 i i i 次操作,位于 1 1 1 号位的期望为 d p i , 0 dp_{i,0} dpi,0, 位于非 1 1 1 号位的期望为 d p i , 1 dp_{i,1} dpi,1
那么,黑球惨遭移动的概率为 $m = 2\frac{1}{n} \cdot \frac{n-1}{n} = \frac{2(n-1)}{n^2} $
故,黑球纹丝不动的概率为 s = 1 − m s = 1 - m s=1−m
黑球移动到某一个位置的概率为 t o = m o v e n − 1 = 2 n 2 to = \frac{move}{n - 1} = \frac{2}{n^2} to=n−1move=n22
转移为:
d p i , 0 = s ⋅ d p i − 1 , 0 + t o ⋅ d p i − 1 , 1 d p i , 1 = m ⋅ d p i − 1 , 0 + ( 1 − t o ) ⋅ d p i − 1 , 1 dp_{i,0} = s \cdot dp_{i-1,0} + to \cdot dp_{i-1,1} \\ dp_{i,1} = m \cdot dp_{i-1,0} + (1 - to) \cdot dp_{i-1,1} dpi,0=s⋅dpi−1,0+to⋅dpi−1,1dpi,1=m⋅dpi−1,0+(1−to)⋅dpi−1,1
最后,因为 p 1 = d p k , 0 p 2 = p 3 = p 4 = . . . = p n = d p k , 1 n − 1 p_1 = dp_{k,0} \ p_2 = p_3 = p_4 = ... = p_n = \frac{dp_{k,1}}{n-1} p1=dpk,0 p2=p3=p4=...=pn=n−1dpk,1
由期望计算公式
E
(
X
)
=
∑
i
=
1
n
i
p
i
E(X) = \sum_{i = 1}^n ip_i
E(X)=i=1∑nipi
本题的答案
a
n
s
=
∑
i
=
1
n
i
p
i
=
d
p
k
,
0
+
d
p
k
,
1
n
−
1
∑
i
=
2
n
i
=
d
p
k
,
0
+
(
n
+
2
)
(
n
−
1
)
2
⋅
d
p
k
,
1
n
−
1
=
(
n
+
2
)
d
p
k
,
1
2
+
d
p
k
,
0
ans = \sum_{i = 1}^n ip_i = dp_{k,0} + \frac{dp_{k,1}}{n-1}\sum_{i = 2}^{n} i = dp_{k,0} + \frac{(n + 2)(n-1)}{2} \cdot \frac{dp_{k,1}}{n-1} = \frac{(n + 2)dp_{k,1}}{2} + dp_{k,0}
ans=i=1∑nipi=dpk,0+n−1dpk,1i=2∑ni=dpk,0+2(n+2)(n−1)⋅n−1dpk,1=2(n+2)dpk,1+dpk,0
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int mod = 998244353;
int qpow(int x,int k) {
int res = 1;
while(k) {
if(k & 1) res = (res * x) % mod;
x = (x * x) % mod;
k >>= 1;
}
return res;
}
int inv(int x) {
return qpow(x,mod - 2) % mod;
}
int dp[100005][2];
signed main() {
int n = rd(),k = rd();
if(n == 1) {
wt(1);
return 0;
}
dp[0][0] = 1;
int P = inv(n);
int P2 = (P * P) % mod;
int move = ((n-1)<<1) % mod * P2 % mod;
int stay = (1 - move + mod) % mod,to = (P2<<1) % mod;
for(int i = 1;i<=k;i++) {
dp[i][0] = (dp[i-1][0] * stay % mod + dp[i-1][1] * to % mod) % mod;
dp[i][1] = (dp[i-1][0] * move % mod + dp[i-1][1] * ((1- to + mod) % mod) %mod) % mod;
}
int ans = dp[k][0] + ((n + 2) * (n - 1) / 2) % mod * dp[k][1] % mod * inv(n-1) % mod;
wt(ans % mod);
return 0;
}
G - Suitable Edit for LIS
问题陈述
给你一个长度为 N N N 的整数序列 A A A 。高桥将执行下列操作一次:
- 在 1 1 1 和 N N N 之间选择一个整数 x x x ,以及一个任意整数 y y y 。将 A x A_x Ax 替换为 y y y 。
求操作后 A A A 的最长递增子序列(LIS)的最大可能长度。
什么是最长递增子序列?
序列 A A A 的子序列是从 A A A 中抽取一些元素而不改变顺序得到的序列。
序列 A A A 的最长递增子序列是严格递增的 A A A 的最长子序列。
看到题目,自然想到预处理出 p r e , s u f pre,suf pre,suf 用来记录 i i i 位前后,以 i i i 为 终点/起点 的 LIS,最后拼起来
图方便就用 unordered_map <int,int> 来充当 树状数组
前后各遍历一次,就可求出 p r e , s u f pre,suf pre,suf 数组
剩下的参考 SJH_qwq 的 题解
AC-code:
#include<bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int inf = 1e9+7;
struct BIT{
#define lowbit(x) (x &(-x))
unordered_map<int,int> c;
void add(int x,int d){
while(x <= inf) {
c[x] = max(c[x],d);
x += lowbit(x);
}
}
int query(int x){
int res = 0;
while(x) {
res = max(res,c[x]);
x -= lowbit(x);
}
return res;
}
}t;
signed main() {
int n = rd();
vector<int> a(n + 2),r(n + 2),l(n + 2);
for(int i = 1;i<=n;i++) a[i] = rd();
int ans = 0;
for(int i = 1;i<=n;i++) {
r[i] = t.query(a[i] - 1) + 1;
t.add(a[i],r[i]);
ans = max(ans,r[i] + (i != n));
}
t.c.clear();
for(int i = n;i >= 1;i--) {
l[i] = t.query(inf - a[i] - 1) + 1;
t.add(inf - a[i],l[i]);
ans = max(ans,l[i] + (i != 1));
}
t.c.clear();
for(int i = 1;i<=n;i++) {
int k = t.query(a[i + 1]);
ans = max(ans,l[i + 1] + k + 1);
t.add(a[i] + 2,r[i]);
}
wt(ans);
return 0;
}
2024/07/08
P4587 [FJOI2016] 神秘数
题面:
题目描述
一个可重复数字集合 S S S 的神秘数定义为最小的不能被 S S S 的子集的和表示的正整数。例如 S = { 1 , 1 , 1 , 4 , 13 } S=\{1,1,1,4,13\} S={1,1,1,4,13},有: 1 = 1 1 = 1 1=1, 2 = 1 + 1 2 = 1+1 2=1+1, 3 = 1 + 1 + 1 3 = 1+1+1 3=1+1+1, 4 = 4 4 = 4 4=4, 5 = 4 + 1 5 = 4+1 5=4+1, 6 = 4 + 1 + 1 6 = 4+1+1 6=4+1+1, 7 = 4 + 1 + 1 + 1 7 = 4+1+1+1 7=4+1+1+1。
8 8 8 无法表示为集合 S S S 的子集的和,故集合 S S S 的神秘数为 8 8 8。
现给定长度为 n n n 的正整数序列 a a a, m m m 次询问,每次询问包含两个参数 l , r l,r l,r,你需要求出由 a l , a l + 1 , ⋯ , a r a_l,a_{l+1},\cdots,a_r al,al+1,⋯,ar 所组成的可重集合的神秘数。
输入格式
第一行一个整数 n n n,表示数字个数。
第二行 n n n 个正整数,从 1 1 1 编号。
第三行一个整数 m m m,表示询问个数。
输出格式
对于每个询问,输出一行对应的答案。
样例 #1
样例输入 #1
5 1 2 4 9 10 5 1 1 1 2 1 3 1 4 1 5样例输出 #1
2 4 8 8 8提示
对于 100 % 100\% 100% 的数据点, 1 ≤ n , m ≤ 10 5 1\le n,m\le {10}^5 1≤n,m≤105, ∑ a ≤ 10 9 \sum a\le {10}^9 ∑a≤109。
可持久线段树的典题
我们假设已经知道 可重集 { a ∣ a ∈ A [ l , r ] } \{a | a \in A[l,r]\} {a∣a∈A[l,r]} 中的数字可以组成的数的最小连续范围为 [ 0 , m a x n ] [0,maxn] [0,maxn]
我们向可重集里插入一个数 a r + 1 a_{r + 1} ar+1 ,观察有什么情况
如果 $a_{r + 1} \in [0,maxn + 1] $,因为可以通过给 a r + 1 a_{r + 1} ar+1 加上 [ 1 , m a x n ] [1,maxn] [1,maxn] 中的任意一个数 ,将可重集扩展到 [ 0 , m a x n + a r + 1 ] [0,maxn + a_{r + 1}] [0,maxn+ar+1]
如果 a r + 1 ∉ [ 0 , m a x n + 1 ] a_{r + 1}\not \in [0,maxn + 1] ar+1∈[0,maxn+1] ,在 m a x n + 1 maxn + 1 maxn+1 处必然有个缺口,致使答案为 m a x n + 1 maxn + 1 maxn+1
令缺口值为 a n s = m a x n + 1 ans = maxn + 1 ans=maxn+1
那么问题就简单了,我们从 [ 0 , 1 ] [0,1] [0,1] 逐步考究一段区间
对于 [ 0 , 1 ] [0,1] [0,1] 我们可以得到 [ l , r ] [l,r] [l,r] 中有多少个 1 1 1,累加到域中,得到 [ 0 , 1 ] → [ 0 , a n s 1 ] [0,1] \rightarrow [0,ans_1] [0,1]→[0,ans1]
然后,对于 [ 0 , a n s 1 ] [0,ans_1] [0,ans1],由于我们已经将 [ 0 , 1 ] [0,1] [0,1] 中的所有数字累加到域中了,那么我们自然从域 [ 2 , a n s 1 ] [2,ans_1] [2,ans1] 中累加数字,得到 [ 0 , a n s 1 ] → [ 0 , a n s 2 ] [0,ans_1]\rightarrow[0,ans_2] [0,ans1]→[0,ans2]
然后,对于 [ 0 , a n s 2 ] [0,ans_2] [0,ans2],由于我们已经将 [ 0 , a n s 1 ] [0,ans_1] [0,ans1] 的数字全部累加完了,我们只需要累加 [ a n s 1 + 1 ] [ans_1 + 1] [ans1+1] 中的数字,得到 [ 0 , a n s 2 ] → [ 0 , a n s 3 ] [0,ans_2] \rightarrow [0,ans_3] [0,ans2]→[0,ans3]
以此类推,就得到:
在添加完 [ 0 , r ] [0,r] [0,r] 和 [ 0 , l − 1 ] [0,l-1] [0,l−1] 两个时间戳内的数字
对于 [ 0 , l a s t a n s ] , 将 [ l , r ] 中 [ l a s t a n s + 1 , a n s ] 扩展到 [ 0 , a n s ] 中,使 [ 0 , a n s ] → [ 0 , n e w a n s ] 其中 [ 0 , l a s t a n s ] 是上一次已经累加过的区域, [ l a s t a n s + 1 , a n s ] 是询问时未累加的区域 , [ 0 , n e w a n s ] 是新的扩展域 对于 [0,lastans]\ ,\ 将\ [l,r]\ 中[lastans + 1,ans]扩展到 [0,ans] 中,使 [0,ans] \rightarrow [0,newans] \\ 其中 [0,lastans] 是上一次已经累加过的区域,[lastans + 1,ans]是询问时未累加的区域,[0,newans] 是新的扩展域 对于[0,lastans] , 将 [l,r] 中[lastans+1,ans]扩展到[0,ans]中,使[0,ans]→[0,newans]其中[0,lastans]是上一次已经累加过的区域,[lastans+1,ans]是询问时未累加的区域,[0,newans]是新的扩展域
直到无法继续累加为止,输出 a n s ans ans,即可
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 1e5+5,inf = 1e9;
int rt[N<<2],cnt;
namespace sgt{
struct seg{
int v,ls,rs;
}t[N<<8];
#define v(p) t[(p)].v
#define ls(p) t[(p)].ls
#define rs(p) t[(p)].rs
#define mid ((pl + pr) >> 1)
void push_up(int p) {
v(p) = v(ls(p)) + v(rs(p));
}
void update(int r,int &p,int pl,int pr,int q,int V){
if(!p) p = ++cnt;
if(pl == pr) {
v(p) += V;
return;
}
if(q <= mid) {
rs(p) = rs(r);
ls(p) = ++cnt;
t[ls(p)] = t[ls(r)];
update(ls(r),ls(p),pl,mid,q,V);
}else {
ls(p) = ls(r);
rs(p) = ++cnt;
t[rs(p)] = t[rs(r)];
update(rs(r),rs(p),mid+1,pr,q,V);
}
push_up(p);
}
int query(int r,int p,int pl,int pr,int ql,int qr){
if(ql <= pl && pr <= qr) return v(p) - v(r);
int res = 0;
if(ql <= mid) res += query(ls(r),ls(p),pl,mid,ql,qr);
if(qr > mid) res += query(rs(r),rs(p),mid+1,pr,ql,qr);
return res;
}
}
int n,m;
signed main() {
n = rd();
for(int i = 1;i<=n;i++) {
int t = rd();
sgt::update(rt[i-1],rt[i],1,inf,t,t);
}
m = rd();
while(m--) {
int ans = 1,l = rd(),r = rd(),lst = 0;
while(1) {
int res = sgt::query(rt[l - 1],rt[r],1,inf,lst + 1,ans);
lst = ans;
if(res) ans = res + ans;
else break;
}
wt(ans),putchar('\n');
}
return 0;
}
P3380 树套树
有人没有写动态开点,我不说是谁
空间爆炸的代码
DEAD-code:
#include<bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int M = 5e4+5;
int n,m,a[M];
struct FHQ{
int cnt = 0,root = 0;
struct node{
int ls,rs;
int key,pri;
int size;
};
#define ls(p) t[p].ls
#define rs(p) t[p].rs
#define pri(p) t[p].pri
void newnode(int x) {
cnt++;
t[cnt].size = 1;
t[cnt].ls = t[cnt].rs = 0;
t[cnt].key = x;
t[cnt].pri = rand();
}
void update(int u) {
t[u].size = t[ls(u)].size + t[rs(u)].size + 1;
}
void spilt(int u,int x,int &L,int &R) {
if(u == 0) {L = R = 0;return;}
if(t[u].key <= x) {
L = u;
spilt(rs(u),x,rs(u),R);
}else {
R = u;
spilt(ls(u),x,L,ls(u));
}
update(u);
}
int merge(int L,int R) {
if(L == 0 || R == 0 ) return L + R;
if(pri(L) > pri(R)) {
rs(L) = merge(rs(L),R);
update(L);
return L;
}else {
ls(R) = merge(L,ls(R));
update(R);
return R;
}
}
void insert(int x) {
int L,R;
spilt(root,x,L,R);
newnode(x);
int aa = merge(L,cnt);
root = merge(aa,R);
}
void del(int x){
int L,R,p;
spilt(root,x,L,R);
spilt(L,x-1,L,p);
p = merge(ls(p),rs(p));
root = merge(merge(L,p),R);
}
int rank(int x){
int L,R;
spilt(root,x-1,L,R);
int rv = t[L].size + 1;
root = merge(L,R);
return rv;
}
int kth(int u,int k) {
if(k == t[ls(u)].size + 1) return u;
if(k <= t[ls(u)].size) return kth(ls(u),k);
if(k > t[ls(u)].size) return kth(rs(u),k - t[ls(u)].size - 1);
}
int pre(int x) {
int L,R;
spilt(root,x-1,L,R);
int rv = t[kth(L,t[L].size)].key;
root = merge(L,R);
return rv;
}
int suc(int x) {
int L,R;
spilt(root,x,L,R);
int rv = t[kth(R,1)].key;
root = merge(L,R);
return rv;
}
#undef ls
#undef rs
#undef mid
};
const int inf = 2147483647;
namespace sgt{
FHQ t[M<<2];
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
void build(int p,int pl,int pr){
for(int i = pl;i<=pr;i++) t[p].insert(a[pl]);
t[p].insert(inf),t[p].insert(-inf);
if(pl == pr) return;
build(ls,pl,mid);
build(rs,mid+1,pr);
}
void update(int p,int pl,int pr,int k,int v){
t[p].del(a[k]);
t[p].insert(v);
if(pl == pr) return;
if(k <= mid) update(ls,pl,mid,k,v);
else update(rs,mid+1,pr,k,v);
}
int getrank(int p,int pl,int pr,int l,int r,int k){
if(l <= pl && pr <= r) return t[p].rank(k);
if(r <= mid) {
return getrank(ls,pl,mid,l,r,k);
} else if(l > mid) {
return getrank(rs,mid+1,pr,l,r,k);
}else {
int m = getrank(ls,pl,mid,l,r,k),n = getrank(rs,mid+1,pr,l,r,k);
return m + n;
}
}
int getkth(int pl,int pr,int k) {
int l = 0,r = 1e8;
while(l < r) {
int Mid = (l + r + 1) / 2;
if(getrank(1,1,n,pl,pr,Mid) < k)
l = Mid;
else r = Mid - 1;
}
return r;
}
int getpre(int p,int pl,int pr,int l,int r,int k){
if(l <= pl && pr <= r) return t[p].pre(k);
if(r <= mid) return getpre(ls,pl,mid,l,r,k);
else if(l > mid) return getpre(rs,mid+1,pr,l,r,k);
else {
int m = getpre(ls,pl,mid,l,r,k),n = getpre(rs,mid+1,pr,l,r,k);
return min(m,n);
}
}
int getsuc(int p,int pl,int pr,int l,int r,int k) {
if(l <= pl && pr <= r) return t[p].suc(k);
if(r <= mid) return getsuc(ls,pl,mid,l,r,k);
else if(l > mid) return getsuc(rs,mid+1,pr,l,r,k);
else {
int m = getsuc(ls,pl,mid,l,r,k),n = getsuc(rs,mid+1,pr,l,r,k);
return max(m,n);
}
}
#undef ls
#undef rs
#undef mid
}
signed main() {
n = rd(),m = rd();
for(int i = 1;i<=n;i++) a[i] = rd();
sgt::build(1,1,n);
while(m--) {
int opt = rd();
int l = rd(),r = rd(),k = rd();
switch (opt)
{
case 1:
wt(sgt::getrank(1,1,n,l,r,k));
putchar('\n');
break;
case 2:
wt(sgt::getkth(l,r,k));
putchar('\n');
break;
case 3:
sgt::update(1,1,n,l,r);
break;
case 4:
wt(sgt::getpre(1,1,n,l,r,k));
putchar('\n');
break;
case 5:
wt(sgt::getsuc(1,1,n,l,r,k));
putchar('\n');
break;
}
}
return 0;
}
这下不得不练动态开点线段树了
template:
struct segment_tree
{
int sum,lson,rson;
}tree[maxq<<2];
int tot;
void update(int &pos,int l,int r,int k)
{
int mid=(l+r)>>1;
if(!pos)
pos=++tot;
if(l==r)
{
tree[pos].sum+=k;
return;
}
if(x<=mid)
update(tree[pos].lson,l,mid,k);
if(y>mid)
update(tree[pos].rson,mid+1,r,k);
tree[pos].sum=tree[tree[pos].lson].sum+tree[tree[pos].rson].sum;
}
int main()
{
int root=0;
update(root,1,maxn,k);
return 0;
}
树套树今天就先鸽着 (写了一下午)(难绷
动态开点线段树
P5459 [BJOI2016] 回转寿司
动态开点练手题
新手村的题目属于是
题面:
题目描述
酷爱日料的小Z经常光顾学校东门外的回转寿司店。在这里,一盘盘寿司通过传送带依次呈现在小Z眼前。
不同的寿司带给小Z的味觉感受是不一样的,我们定义小Z对每盘寿司都有一个满意度。
例如小Z酷爱三文鱼,他对一盘三文鱼寿司的满意度为 10 10 10;小Z觉得金枪鱼没有什么味道,他对一盘金枪鱼寿司的满意度只有 5 5 5;小Z最近看了电影《美人鱼》,被里面的八爪鱼恶心到了,所以他对一盘八爪鱼刺身的满意度是 − 100 -100 −100。
特别地,小Z是个著名的吃货,他吃回转寿司有一个习惯,我们称之为“狂吃不止”。具体地讲,当他吃掉传送带上的一盘寿司后,他会毫不犹豫地吃掉它后面的寿司,直到他不想再吃寿司了为止。
今天,小Z再次来到了这家回转寿司店, N N N 盘寿司将依次经过他的面前。其中,小Z对第 i i i 盘寿司的满意度为 a i a_i ai。
小Z可以选择从哪盘寿司开始吃,也可以选择吃到哪盘寿司为止。他想知道共有多少种不同的选择,使得他的满意度之和不低于 L L L,且不高于 R R R。
注意,虽然这是回转寿司,但是我们不认为这是一个环上的问题,而是一条线上的问题。即,小Z能吃到的是输入序列的一个连续子序列;最后一盘转走之后,第一盘并不会再出现一次。
输入格式
第一行三个正整数 N , L , R N,L,R N,L,R,表示寿司盘数,满意度的下限和上限。
第二行包含 N N N 个整数 a i a_i ai,表示小Z对寿司的满意度。输出格式
一行一个整数,表示有多少种方案可以使得小Z的满意度之和不低于 L L L 且不高于 R R R。
样例 #1
样例输入 #1
5 5 9 1 2 3 4 5样例输出 #1
6提示
【数据范围】
1 ≤ N ≤ 1 0 5 1\le N \le 10^5 1≤N≤105
∣ a i ∣ ≤ 1 0 5 |a_i| \le 10^5 ∣ai∣≤105
0 ≤ L , R ≤ 1 0 9 0\le L,R \le 10^9 0≤L,R≤109
形式化的:
我们需要在序列中找出所有满足
对于
i
<
j
,
∑
k
=
i
j
a
k
∈
[
L
,
R
]
对于 i < j ,\sum_{k = i}^j a_k \in [L,R]
对于i<j,k=i∑jak∈[L,R]
的子序列
[
i
,
j
]
[i,j]
[i,j] 的个数
看到这题,自然会想到 逆序对统计、加入循环的思路
本题也是一样
既然题目中有 ∑ \sum ∑,那我们就先用前缀和先处理出来
然后,插入一个前缀和,找 k − R ∼ k − L k - R \sim k - L k−R∼k−L 中的个数
统计出来就结束了
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 1e5+5,inf = 1e18;
int n,l,r,a[N];
namespace sgt{
#define mid ((pl + pr) >> 1)
int t[N * 34 * 4 + 5],cnt,ls[N * 34 * 4 + 5],rs[N * 34 * 4 + 5];
int root = 0;
void push_up(int p) {
t[p] = t[ls[p]] + t[rs[p]];
}
void update(int &p,int k,int d,int pl = -inf,int pr = inf) {
if(!p) p = ++cnt;
if(pl == pr) {t[p] += d;return;}
if(k <= mid) update(ls[p],k,d,pl,mid);
else update(rs[p],k,d,mid+1,pr);
push_up(p);
}
int query(int &p,int l,int r,int pl = -inf,int pr = inf) {
if(!p) return 0;
if(l <= pl && pr <= r) return t[p];
int res = 0;
if(l <= mid) res += query(ls[p],l,r,pl,mid);
if(r > mid) res += query(rs[p],l,r,mid+1,pr);
return res;
}
#undef ls
#undef rs
#undef mid
}
int ans = 0;
signed main() {
n = rd(),l = rd(),r = rd();
for(int i = 1;i<=n;i++) a[i] = rd();
for(int i = 1;i<=n;i++) a[i] = a[i-1] + a[i];
sgt::update(sgt::root,a[0],1);
for(int i = 1;i<=n;i++) {
ans += sgt::query(sgt::root,a[i] - r,a[i] - l);
sgt::update(sgt::root,a[i],1);
}
wt(ans);
putchar('\n');
return 0;
}
P3960 [NOIP2017 提高组] 列队
题面:
题目背景
NOIP2017 D2T3
题目描述
Sylvia是一个热爱学习的女孩子。前段时间,
Sylvia参加了学校的军训。众所周知,军训的时候需要站方阵。Sylvia 所在的方阵中有 n × m n \times m n×m 名学生,方阵的行数为 n n n,列数为 m m m。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 1 1 到 n × m n \times m n×m 编上了号码(参见后面的样例)。即:初始时,第 i i i 行第 j j j 列 的学生的编号是 ( i − 1 ) × m + j (i-1)\times m + j (i−1)×m+j。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 q q q 件这样的离队事件。每一次离队事件可以用数对 ( x , y ) ( 1 ≤ x ≤ n , 1 ≤ y ≤ m ) (x,y) (1 \le x \le n, 1 \le y \le m) (x,y)(1≤x≤n,1≤y≤m) >描述,表示第 x x x 行第 y y y 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
- 向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 x x x 行第 m m m 列。
- 向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 n n n 行第 m m m 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 n n n 行 第 m m m 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以
Sylvia想要计算每一次离队事件中,离队的同学 的编号是多少。注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
输入格式
输入共 q + 1 q+1 q+1 行。
第一行包含 3 3 3 个用空格分隔的正整数 n , m , q n, m, q n,m,q,表示方阵大小是 n n n 行 m m m 列,一共发 生了 q q q 次事件。
接下来 q q q 行按照事件发生顺序描述了 q q q 件事件。每一行是两个整数 x , y x, y x,y,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 x x x 行第 y y y 列。
输出格式
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学生的编号。
样例 #1
样例输入 #1
2 2 3 1 1 2 2 1 2样例输出 #1
1 1 4提示
【输入输出样例 1 1 1 说明】
[ 1 2 3 4 ] ⇒ [ 2 3 4 ] ⇒ [ 2 3 4 ] ⇒ [ 2 4 3 ] ⇒ [ 2 4 3 1 ] [ 2 4 3 1 ] ⇒ [ 2 4 3 ] ⇒ [ 2 4 3 ] ⇒ [ 2 4 3 ] ⇒ [ 2 4 3 1 ] [ 2 4 3 1 ] ⇒ [ 2 3 1 ] ⇒ [ 2 3 1 ] ⇒ [ 2 1 3 ] ⇒ [ 2 1 3 4 ] \begin{matrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} & 2 \\ 3 & 4 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & \\ 3 & 4 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 4 \\ 3 & \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 4 \\ 3 & 1 \\ \end{bmatrix} \\[1em] \begin{bmatrix} 2 & 4 \\ 3 & 1 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 4 \\ 3 & \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 4 \\ 3 & \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 4 \\ 3 & \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 4 \\ 3 & 1 \\ \end{bmatrix}\\[1em] \begin{bmatrix} 2 & 4 \\ 3 & 1 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & \\ 3 & 1 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & \\ 3 & 1 \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 1 \\ 3 & \\ \end{bmatrix} & \Rightarrow & \begin{bmatrix} 2 & 1 \\ 3 & 4 \\ \end{bmatrix} \end{matrix} [1324][2341][2341]⇒⇒⇒[324][234][231]⇒⇒⇒[234][234][231]⇒⇒⇒[234][234][231]⇒⇒⇒[2341][2341][2314]
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为 1 1 1 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 2 2 2 的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为 4 4 4 的同学向上一步,这时空位移动到第二行第二列。最后编号为 1 1 1 的同学返回填补到空位中。
【数据规模与约定】
测试点编号 n n n m m m q q q 其他约定 1 ∼ 6 1\sim 6 1∼6 ≤ 1 0 3 \le 10^3 ≤103 ≤ 1 0 3 \le 10^3 ≤103 ≤ 500 \le 500 ≤500 无 7 ∼ 10 7\sim 10 7∼10 ≤ 5 × 1 0 4 \le 5\times 10^4 ≤5×104 ≤ 5 × 1 0 4 \le 5\times 10^4 ≤5×104 ≤ 500 \le 500 ≤500 无 11 ∼ 12 11\sim 12 11∼12 = 1 =1 =1 ≤ 1 0 5 \le 10^5 ≤105 ≤ 1 0 5 \le 10^5 ≤105 所有事件 x = 1 x=1 x=1 13 ∼ 14 13\sim 14 13∼14 = 1 =1 =1 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 所有事件 x = 1 x=1 x=1 15 ∼ 16 15\sim 16 15∼16 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 所有事件 x = 1 x=1 x=1 17 ∼ 18 17\sim 18 17∼18 ≤ 1 0 5 \le 10^5 ≤105 ≤ 1 0 5 \le 10^5 ≤105 ≤ 1 0 5 \le 10^5 ≤105 无 19 ∼ 20 19\sim 20 19∼20 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 ≤ 3 × 1 0 5 \le 3\times 10^5 ≤3×105 无 数据保证每一个事件满足 1 ≤ x ≤ n , 1 ≤ y ≤ m 1 \le x \le n,1 \le y \le m 1≤x≤n,1≤y≤m。
待补
P8818 [CSP-S 2022] 策略游戏
题面:
题目描述
小 L 和小 Q 在玩一个策略游戏。
有一个长度为 n n n 的数组 A A A 和一个长度为 m m m 的数组 B B B,在此基础上定义一个大小为 n × m n \times m n×m 的矩阵 C C C,满足 C i j = A i × B j C_{i j} = A_i \times B_j Cij=Ai×Bj。所有>下标均从 1 1 1 开始。
游戏一共会进行 q q q 轮,在每一轮游戏中,会事先给出 4 4 4 个参数 l 1 , r 1 , l 2 , r 2 l_1, r_1, l_2, r_2 l1,r1,l2,r2,满足 1 ≤ l 1 ≤ r 1 ≤ n 1 \le l_1 \le r_1 \le n 1≤l1≤r1≤n、 1 ≤ l 2 ≤ r 2 ≤ m 1 \le l_2 \le r_2 \le m 1≤l2≤r2≤m。
游戏中,小 L 先选择一个 l 1 ∼ r 1 l_1 \sim r_1 l1∼r1 之间的下标 x x x,然后小 Q 选择一个 l 2 ∼ r 2 l_2 \sim r_2 l2∼r2 之间的下标 y y y。定义这一轮游戏中二人的得分是 C x y C_{x y} Cxy。
小 L 的目标是使得这个得分尽可能大,小 Q 的目标是使得这个得分尽可能小。同时两人都是足够聪明的玩家,每次都会采用最优的策略。
请问:按照二人的最优策略,每轮游戏的得分分别是多少?
输入格式
第一行输入三个正整数 n , m , q n, m, q n,m,q,分别表示数组 A A A,数组 B B B 的长度和游戏轮数。
第二行: n n n 个整数,表示 A i A_i Ai,分别表示数组 A A A 的元素。
第三行: m m m 个整数,表示 B i B_i Bi,分别表示数组 B B B 的元素。
接下来 q q q 行,每行四个正整数,表示这一次游戏的 l 1 , r 1 , l 2 , r 2 l_1, r_1, l_2, r_2 l1,r1,l2,r2。
输出格式
输出共 q q q 行,每行一个整数,分别表示每一轮游戏中,小 L 和小 Q 在最优策略下的得分。
样例 #1
样例输入 #1
3 2 2 0 1 -2 -3 4 1 3 1 2 2 3 2 2样例输出 #1
0 4样例 #2
样例输入 #2
6 4 5 3 -1 -2 1 2 0 1 2 -1 -3 1 6 1 4 1 5 1 4 1 4 1 2 2 6 3 4 2 5 2 3样例输出 #2
0 -2 3 2 -1提示
【样例解释 #1】
这组数据中,矩阵 C C C 如下:
[ 0 0 − 3 4 6 − 8 ] \begin{bmatrix} 0 & 0 \\ -3 & 4 \\ 6 & -8 \end{bmatrix} 0−3604−8
在第一轮游戏中,无论小 L 选取的是 x = 2 x = 2 x=2 还是 x = 3 x = 3 x=3,小 Q 都有办法选择某个 y y y 使得最终的得分为负数。因此小 L 选择 x = 1 x = 1 x=1 是最优的,因为这样得>分一定为 0 0 0。
而在第二轮游戏中,由于小 L 可以选 x = 2 x = 2 x=2,小 Q 只能选 y = 2 y = 2 y=2,如此得分为 4 4 4。
【样例 #3】
见附件中的
game/game3.in与game/game3.ans。【样例 #4】
见附件中的
game/game4.in与game/game4.ans。【数据范围】
对于所有数据, 1 ≤ n , m , q ≤ 10 5 1 \le n, m, q \le {10}^5 1≤n,m,q≤105, − 10 9 ≤ A i , B i ≤ 10 9 -{10}^9 \le A_i, B_i \le {10}^9 −109≤Ai,Bi≤109。对于每轮游戏而言, 1 ≤ l 1 ≤ r 1 ≤ n 1 \le l_1 \le r_1 \le n 1≤l1≤r1≤n, 1 ≤ l 2 ≤ r 2 ≤ m 1 \le l_2 \le r_2 \le m 1≤l2≤r2≤m。
测试点编号 n , m , q ≤ n, m, q \le n,m,q≤ 特殊条件 1 1 1 200 200 200 1, 2 2 2 2 200 200 200 1 3 3 3 200 200 200 2 4 ∼ 5 4 \sim 5 4∼5 200 200 200 无 6 6 6 1000 1000 1000 1, 2 7 ∼ 8 7 \sim 8 7∼8 1000 1000 1000 1 9 ∼ 10 9 \sim 10 9∼10 1000 1000 1000 2 11 ∼ 12 11 \sim 12 11∼12 1000 1000 1000 无 13 13 13 10 5 {10}^5 105 1, 2 14 ∼ 15 14 \sim 15 14∼15 10 5 {10}^5 105 1 16 ∼ 17 16 \sim 17 16∼17 10 5 {10}^5 105 2 18 ∼ 20 18 \sim 20 18∼20 10 5 {10}^5 105 无 其中,特殊性质 1 为:保证 A i , B i > 0 A_i, B_i > 0 Ai,Bi>0。
特殊性质 2 为:保证对于每轮游戏而言,要么 l 1 = r 1 l_1 = r_1 l1=r1,要么 l 2 = r 2 l_2 = r_2 l2=r2。
鉴定为 大分讨
我们直接来分析局面
上图!
首先来分析简单的
我们假设 L L L 先手, Q Q Q 后手
情况 1 ◯ \textcircled{1} 1◯
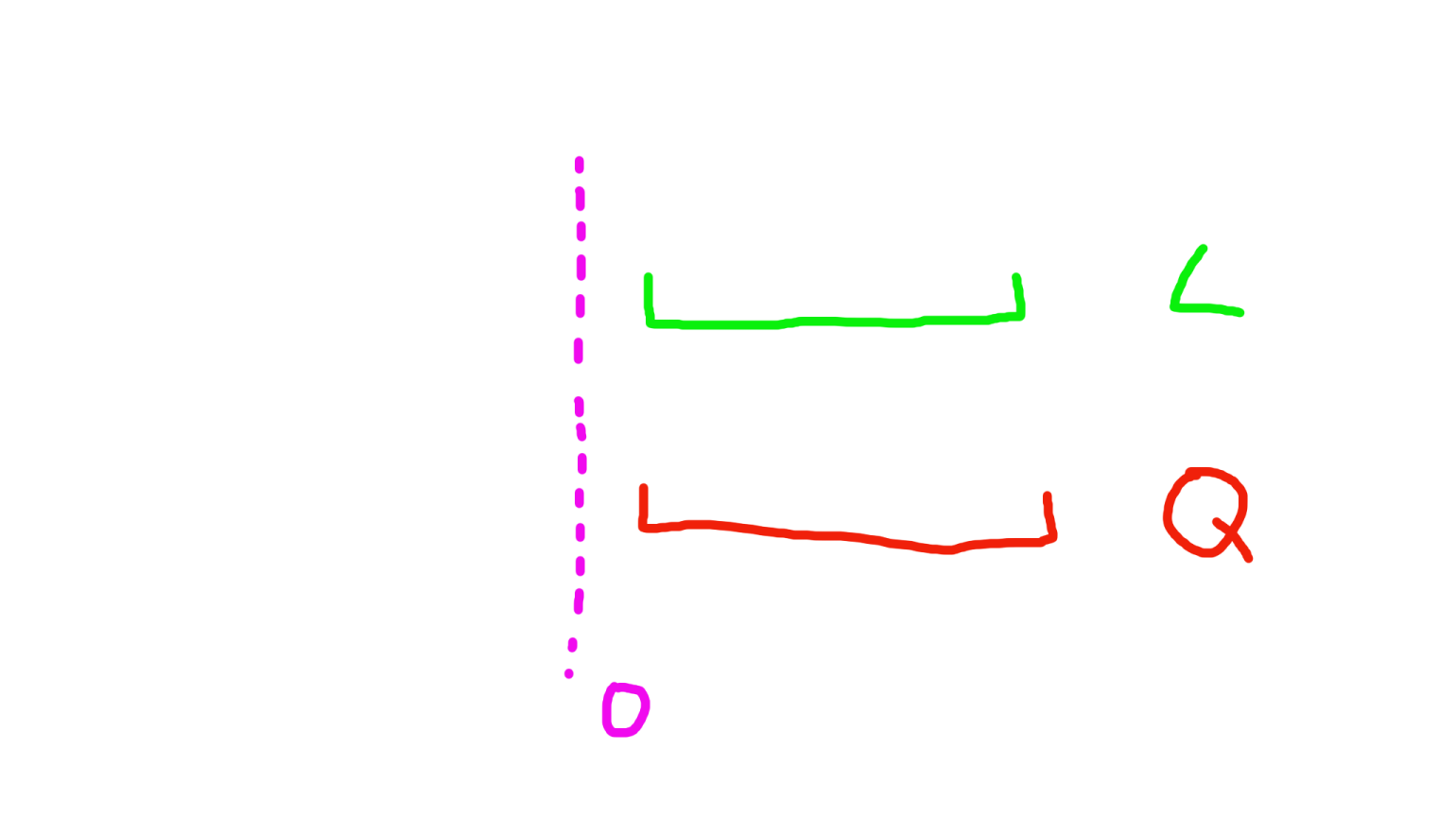
L , Q L,Q L,Q 都在 0 0 0 左侧
L L L 肯定选区间最大值, Q Q Q 肯定选区间最小值
情况 2 ◯ \textcircled{2} 2◯
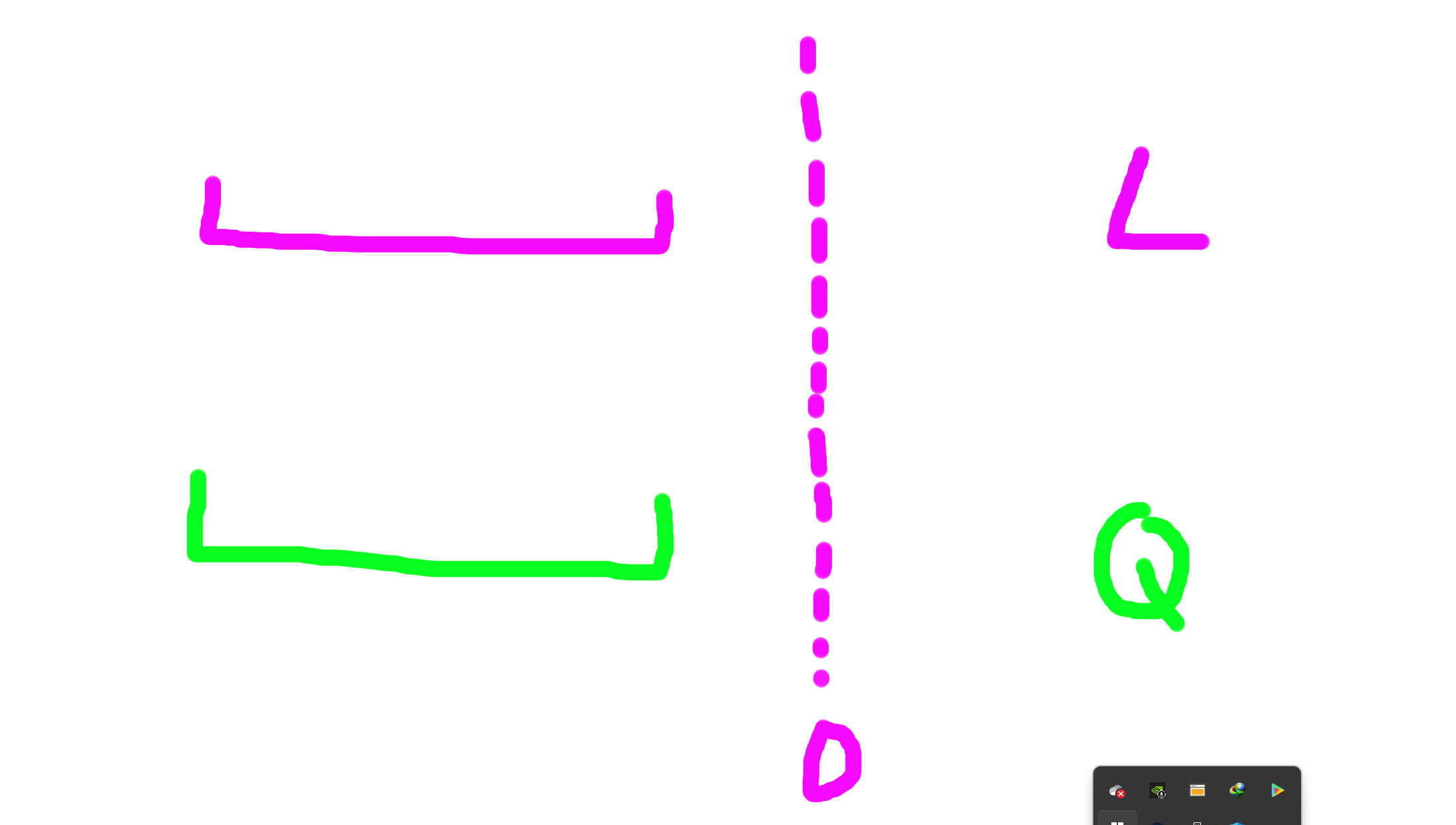
L , Q L,Q L,Q 都在 0 0 0 右侧
L L L 肯定选区间最小值, Q Q Q 肯定选区间最大值
情况 3 ◯ \textcircled{3} 3◯

L L L 肯定选区间最小值, Q Q Q 肯定选区间最小值
情况 4 ◯ \textcircled{4} 4◯
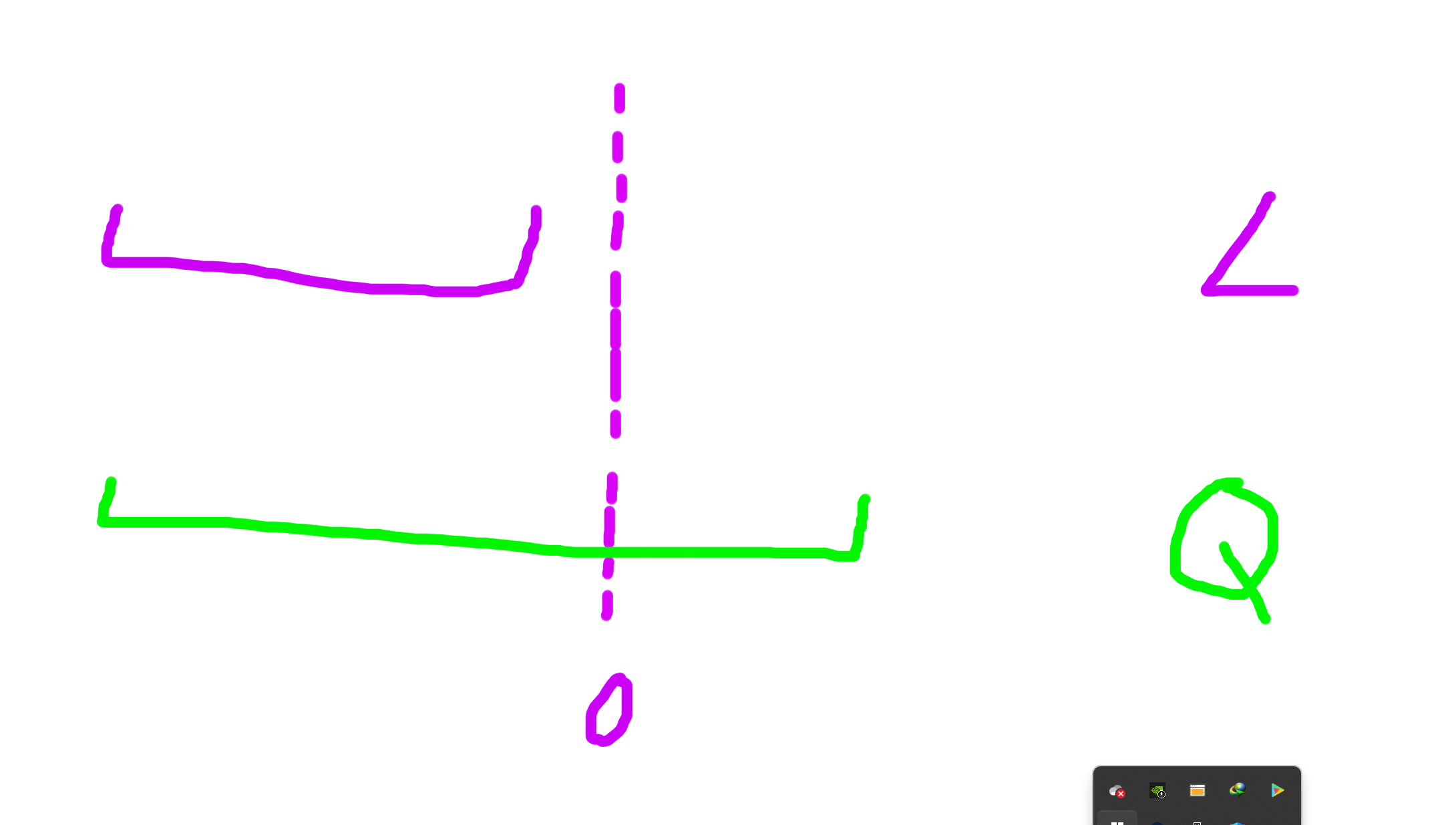
L L L 肯定选区间最小值, Q Q Q 肯定选区间最大值
再然后就比较难想了
情况 5 ◯ \textcircled{5} 5◯
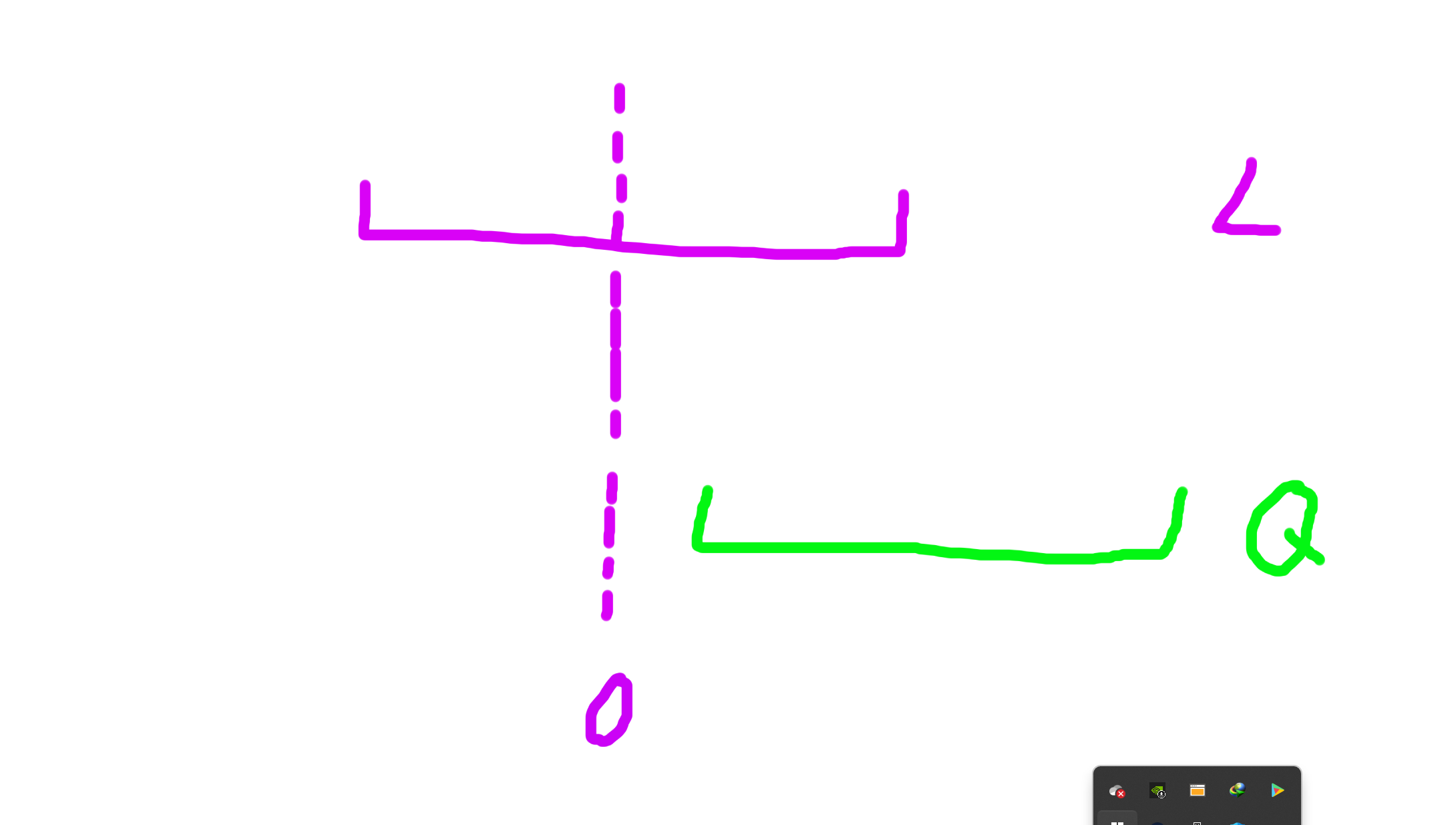
L L L 肯定选区间最大值, Q Q Q 肯定选区间最小值
情况 6 ◯ \textcircled{6} 6◯
L L L 肯定选区间最小值, Q Q Q 肯定选区间最大值
最困难的
情况 7 ◯ → 一般情况 \textcircled{7} \rightarrow 一般情况 7◯→一般情况

作为 L L L,显然取最大值、最小值,都会被反杀
那么,我们就让损失最小化
容易想到,我们取 L , Q L,Q L,Q 靠近 0 0 0 两侧的值
如图:

这样,损失最小
那么我们要特别处理 L L L 序列的非正最大值,非负最小值—我们在线段树里额外维护一下就可以了
此题完美结束!
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int M = 1e5+5,inf = 2139062143;
int n,m,q,a[M];
struct sgt{
#define ls (p << 1)
#define rs (p << 1 | 1)
#define mid ((pl + pr) >> 1)
int mn[M<<2],mx[M<<2];
int _mn[M<<2],_mx[M<<2];
void push_up(int p) {
mn[p] = min(mn[ls],mn[rs]);
mx[p] = max(mx[ls],mx[rs]);
_mn[p] = min(_mn[ls],_mn[rs]);
_mx[p] = max(_mx[ls],_mx[rs]);
}
void build(int p,int pl,int pr){
if(pl == pr) {
mn[p] = mx[p] = a[pl];
_mn[p] = a[pl] >= 0 ? a[pl] : inf;
_mx[p] = a[pl] <= 0 ? a[pl] : -inf;
return;
}
build(ls,pl,mid);
build(rs,mid+1,pr);
push_up(p);
}
int querymax(int p,int pl,int pr,int l,int r) {
if(l <= pl && pr <= r) return mx[p];
int res = -inf;
if(l <= mid) res = max(res,querymax(ls,pl,mid,l,r));
if(r > mid) res = max(res,querymax(rs,mid+1,pr,l,r));
return res;
}
int query_max(int p,int pl,int pr,int l,int r) {
if(l <= pl && pr <= r) return _mx[p];
int res = -inf;
if(l <= mid) res = max(res,query_max(ls,pl,mid,l,r));
if(r > mid) res = max(res,query_max(rs,mid+1,pr,l,r));
return res;
}
int query_min(int p,int pl,int pr,int l,int r){
if(l <= pl && pr <= r) return _mn[p];
int res = inf;
if(l <= mid) res = min(res,query_min(ls,pl,mid,l,r));
if(r > mid) res = min(res,query_min(rs,mid+1,pr,l,r));
return res;
}
int querymin(int p,int pl,int pr,int l,int r) {
if(l <= pl && pr <= r) return mn[p];
int res = inf;
if(l <= mid) res = min(res,querymin(ls,pl,mid,l,r));
if(r > mid) res = min(res,querymin(rs,mid+1,pr,l,r));
return res;
}
}c,d;
signed main() {
n = rd(),m = rd(),q = rd();
for(int i = 1;i<=n;i++) a[i] = rd();
c.build(1,1,n);
for(int i = 1;i<=m;i++) a[i] = rd();
d.build(1,1,m);
while(q--) {
int l1 = rd(),r1 = rd(),l2 = rd(),r2 = rd();
int mna = c.querymin(1,1,n,l1,r1),mnb = d.querymin(1,1,m,l2,r2);
int mxa = c.querymax(1,1,n,l1,r1),mxb = d.querymax(1,1,m,l2,r2);
if(mna >= 0 && mnb >= 0) wt(mxa * mnb);
else if(mxa <= 0 && mxb <= 0) wt(mna * mxb);
else if(mna >= 0 && mnb <= 0) wt(mna * mnb);
else if(mxa <= 0 && mxb >= 0) wt(mxb * mxa);
else if(mna <= 0 && mxa >= 0 && mnb >= 0) wt(mxa * mnb);
else if(mxb <= 0 && mxa >= 0 && mna <= 0) wt(mna * mxb);
else{
int ra = c.query_min(1,1,n,l1,r1),rb = d.querymin(1,1,m,l2,r2);
int ora = c.query_max(1,1,n,l1,r1),orb = d.querymax(1,1,m,l2,r2);
int res = max(ra * rb,ora * orb);
wt(res);
}
putchar('\n');
}
return 0;
}






















 407
407

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








