C. 野火
题目描述
B 国有 座城市,有 条双向道路连接着这些城市。城市编号为 到 ,道路编号为 到 。经由这些道路,从 B 国中任意一个城市出发,均能到达其他所有城市。特别地,这里保证 。
由于能源不足,B 国的第 条道路只能正常运行 个时刻。现在 Yoimiya 需要给每一条道路选择一个开始运行的时间 ,那么这条道路就会在 这些时刻内正常运行。保证 。
B 国的大守护者布洛妮娅想要让国家在尽可能长的一段时间内保持连通。形式化地,对于 Yoimiya 选择的一种方案 ,定义其连通度为最大的正整数 ,使得对任意的 ,在第 个时刻,从 B 国的任意一个城市出发,只通过当前时刻仍在正常运行的道路,仍然可以到达任意另一个城市。大守护者希望找到连通度最大的方案。
随着 B 国的发展,现在 B 国已经可以对道路进行有限的能源扩充。具体地,大守护者可以给第 条道路扩充 个单位的能源,使得其最大运行时间 增大为 。由于能源有限, 的值不能超过给定的正整数 。大守护者想让你协助她找到一种扩充能源的方案 ,使得在扩充能源后,可能的最大连通度尽可能大。你只需要输出可能的最大连通度即可。
输入格式
第一行两个正整数 分别表示测试点编号与数据组数。对于样例有 。
对于每组数据:
第一行三个正整数 。
接下来 行,第 三个正整数 ,表示 B 国存在一条双向道路 ,这条道路一开始最多只能运行 个时刻。
输出格式
对于每组数据,输出一行一个正整数表示可能的最大连通度。
样例
样例 1 输入
0 2
3 3 3
1 2 3
2 1 5
1 3 7
4 4 4
1 2 3
2 3 4
3 1 6
2 4 7
样例 1 输出
9
8
样例 2、3、4
每个样例中都有 组数据,其中第 组满足特殊性质 AB,第 组满足特殊性质 AC,第 组满足特殊性质 A,第 组满足特殊性质 BD,第 组满足特殊性质 CD,第 组满足特殊性质 D,第 组满足特殊性质 B,第 组满足特殊性质 C,第 组可能不满足任何特殊性质。
此外,样例 满足 ,样例 满足 ,样例 满足 。
数据范围与提示
数据范围
对于所有数据,有:
-
;
-
。
| 测试点编号 | 数据范围 | 特殊性质 |
|---|---|---|
| 无 | ||
| AB | ||
| A | ||
| BD | ||
| CD | ||
| D | ||
| 无 | ||
| AC | ||
| AB | ||
| 无 | ||
| AB | ||
| AC | ||
| A | ||
| B | ||
| C | ||
| D | ||
| 无 | ||
其中,各个特殊性质的含义分别为:
-
特殊性质 A: 。
-
特殊性质 B: 。
-
特殊性质 C: 。
-
特殊性质 D: ,对任意 ,且 。
首先 m ≤ n m \leq n m≤n,一上来我还以为我眼花了,这个图还要联通
不是树,就是基环树。
我们以防万一先判断连通性,如果不连通,谈都不用谈,直接输出 0 0 0
然后讨论一下
1 ◯ \textcircled{1} 1◯ 树
最简单的,因为根本没得替补,每条边必须上
那么,我们考虑直接二分答案,去找一找如何补缺口使得每条边能撑过 m i d mid mid
code:
// C[i] 是边 、C[i].d 是边的边权
int check(int lim) {
int res = 0;
for(int i = 1;i<=top;i++)
if(C[i].d < lim)
res += lim - C[i].d;
return res;
}
......
if(m == n - 1) {
int l = 1,r = 3e9 + 5;
while(l < r - 1) {
int mid = (l + r) >> 1;
if(check(mid) <= L) l = mid;
else r = mid;
}
wt(l);
putchar('\n');
}
2 ◯ \textcircled{2} 2◯ 基环树
Q:那么区别在哪呢?
A:环嘛!
Q:那么这个环带来了什么影响呢?
A:这个环的一个边挂掉了后,未响应边能替补上去!
Q:那么替补完后会怎么样呢?
A:另一条边挂掉了,彻底完蛋了!
Q:那么这个环上哪条边会最先挂掉呢?
A:边权最小的地方嘛!
那么,这个替补的操作可以视为 在最小边的边权加上这个替补边的边权,以延长它的寿命
这个替补就是逊了,我们跑一个kruskal求一个最大生成树,留下来的边自然就是替补边
然后我们以替补边的两个端点(肯定在环内),跑一下环(即两点之间的路径)记录一下最小边
因为我们对被加的边是哪一条边没有兴趣,我们只要找到在役边中边权与最小边边权匹配的边,加上这个替补边的边权,就可以和树一样做了
(这个思路还是很自然的,考场没花什么时间,主要是T2细节花了不少时间,还重构了一边)
code:
//vis[] 数组在之前的kruskal中求出了(标记在役边)
if(m == n) {
init_edge();
for(int i = 1;i<=m;i++)
if(vis[i])
add(E[i].v,E[i].u,E[i].d),add(E[i].u,E[i].v,E[i].d); //对在役边建树
dfs1(1,0);
int addition = 0;
for(int i = 1;i<=m;i++)
if(!vis[i])
dfs(E[i].v,E[i].u),addition = E[i].d; // 找替补边
for(int i = 1;i<=top;i++)
if(C[i].d == mn){
C[i].d = mn + addition; //对最小边权匹配的边加上替补边边权
break;
}
int l = 1,r = 3e9 + 5;
while(l < r - 1) {
int mid = (l + r) >> 1;
if(check(mid) <= L) l = mid;
else r = mid;
}
wt(l);
putchar('\n');
}
本题最大坑点:
二分上限是
3
e
9
3e9
3e9,我们考虑这样一个情景: 两个点形成了基环,边权都是讨厌的
1
e
9
1e9
1e9,你还要加上一个
1
e
9
1e9
1e9 的逆天
L
L
L
害我痛失 44 分
本代码复杂度:
O
(
n
+
m
log
V
)
O(n + m\log V)
O(n+mlogV)
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N =2e5+5;
struct edge{
int u,v,d;
friend bool operator < (const edge &a,const edge &b) {
return a.d > b.d;
}
}E[N],C[N];
int s[N],top,n,m,L;
bool vis[N];
void init() {
for(int i = 0;i<=n;i++) s[i] = i;
for(int i = 0;i<=m;i++) vis[i] = false;
}
int find(int x) {if(s[x] ^ x) s[x] = find(s[x]);return s[x];}
void kruskal() {
top = 0;
init();
sort(E + 1,E + m + 1);
int fx,fy,minn = INT_MAX;
for(int i = 1;i<=m;i++) {
fx = find(E[i].v),fy = find(E[i].u);
if(fx == fy) continue;
s[fx] = fy;
vis[i] = true;
C[++top] = E[i];
if(top == n - 1) break;
}
}
int check(int lim) {
int res = 0;
for(int i = 1;i<=top;i++)
if(C[i].d < lim)
res += lim - C[i].d;
return res;
}
int head[N],nxt[N<<1],to[N<<1],val[N<<1],cnt;
void init_edge() {memset(head,-1,sizeof(head));cnt = 0;}
void add(int u,int v,int w) {
nxt[cnt] = head[u];
to[cnt] = v;
val[cnt] = w;
head[u] = cnt++;
}
int fa[N],tp[N],siz[N],son[N],dep[N];
void dfs1(int x,int f) {
dep[x] = dep[f] + 1;
fa[x] = f;
for(int i = head[x];~i;i = nxt[i]) {
int y = to[i];
if(y ^ f)
dfs1(y,x);
}
}
int mn = INT_MAX;
void dfs(int x,int y) {
while(x != y) {
if(dep[x] < dep[y]) swap(x,y);
for(int i = head[x];~i;i = nxt[i]) {
int z = to[i];
if(z == fa[x])
mn = min(mn,val[i]);
}
x = fa[x];
}
}
void solve() {
mn = INT_MAX;
n = rd(),m = rd(),L = rd();
for(int i = 1;i<=m;i++)
E[i].u = rd(),E[i].v = rd(),E[i].d = rd();
kruskal();
if(top != n - 1) {puts("0");return;}
if(m == n - 1) {
int l = 1,r = 3e9 + 5;
while(l < r - 1) {
int mid = (l + r) >> 1;
if(check(mid) <= L) l = mid;
else r = mid;
}
wt(l);
putchar('\n');
}else if(m == n) {
init_edge();
for(int i = 1;i<=m;i++)
if(vis[i])
add(E[i].v,E[i].u,E[i].d),add(E[i].u,E[i].v,E[i].d);
dfs1(1,0);
int addition = 0;
for(int i = 1;i<=m;i++)
if(!vis[i])
dfs(E[i].v,E[i].u),addition = E[i].d;
for(int i = 1;i<=top;i++)
if(C[i].d == mn){
C[i].d = mn + addition;
break;
}
int l = 1,r = 3e9 + 5;
while(l < r - 1) {
int mid = (l + r) >> 1;
if(check(mid) <= L) l = mid;
else r = mid;
}
wt(l);
putchar('\n');
}
}
signed main() {
freopen("wildfire.in","r",stdin);
freopen("wildfire.out","w",stdout);
int id = rd(),T = rd();
while(T--) solve();
return 0;
}
2024/08/08
P1084 [NOIP2012 提高组] 疫情控制
题面:
[NOIP2012 提高组] 疫情控制
题目描述
H 国有 $n $ 个城市,这 n n n 个城市用 $ n-1 $ 条双向道路相互连通构成一棵树,$1 $ 号城市是首都,也是树中的根节点。
H 国的首都爆发了一种危害性极高的传染病。当局为了控制疫情,不让疫情扩散到边境城市(叶子节点所表示的城市),决定动用军队在一些城市建立检查点,使得从首都到边境城市的每一条路径上都至少有一个检查点,边境城市也可以建立检查点。但特别要注意的是,首都是不能建立检查点的。
现在,在 H 国的一些城市中已经驻扎有军队,且一个城市可以驻扎多个军队。一支军队可以在有道路连接的城市间移动,并在除首都以外的任意一个城市建立检查点,且只能在一个城市建立检查点。一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等于道路的长度(单位:小时)。
请问最少需要多少个小时才能控制疫情。注意:不同的军队可以同时移动。
输入格式
第一行一个整数 $ n$,表示城市个数。
接下来的 n − 1 n-1 n−1 行,每行 $ 3 $ 个整数, u , v , w u,v,w u,v,w,每两个整数之间用一个空格隔开,表示从城市 $u $ 到城市 $ v$ 有一条长为 w w w 的道路。数据保证输入的是一棵树,且根节点编号为 1 1 1。
接下来一行一个整数 m m m,表示军队个数。
接下来一行 $m $ 个整数,每两个整数之间用一个空格隔开,分别表示这 m m m 个军队所驻扎的城市的编号。
输出格式
一个整数,表示控制疫情所需要的最少时间。如果无法控制疫情则输出 − 1 -1 −1。
样例 #1
样例输入 #1
4 1 2 1 1 3 2 3 4 3 2 2 2样例输出 #1
3提示
【输入输出样例说明】
第一支军队在 2 2 2 号点设立检查点,第二支军队从 2 2 2 号点移动到$ 3$ 号点设立检查点,所需时间为 3 3 3 个小时。
【数据范围】
保证军队不会驻扎在首都。
- 对于 20 % 20\% 20% 的数据, 2 ≤ n ≤ 10 2 \le n\le 10 2≤n≤10;
- 对于 40 % 40\% 40% 的数据, 2 ≤ n ≤ 50 2 \le n\le 50 2≤n≤50, 0 < w < 1 0 5 0<w <10^5 0<w<105;
- 对于 60 % 60\% 60% 的数据, 2 ≤ n ≤ 1000 2 \le n\le 1000 2≤n≤1000, 0 < w < 1 0 6 0<w <10^6 0<w<106;
- 对于 80 % 80\% 80% 的数据, 2 ≤ n ≤ 1 0 5 2 \le n\le 10^5 2≤n≤105;
- 对于 100 % 100\% 100% 的数据, 2 ≤ m ≤ n ≤ 5 × 1 0 5 2\le m\le n≤ 5\times 10^5 2≤m≤n≤5×105, 0 < w < 1 0 9 0<w <10^9 0<w<109。
t h i s i s h a r d c o d e m o d e this\ is\ hardcode\ mode this is hardcode mode
NOIP 2012 提高组 第二天 第三题
除了细节多,其实理解起来不算难
我们很容易就可以想到,每个军队(仅限不在根节点的)肯定会往上走,往下走肯定不优(控制的节点大幅度减少)
看到这种 求“最少”,不用想都是二分,我们二分这个时间限制,看一看能不能控制住整个树
这就是整个题的难点(“ c h e c k check check desu”)
我们要快速求出每个军队能跑的最浅节点,自然考虑倍增维护 k k k 级父亲和花费
但是军队不能直接到根节点,因为我们要看一看,军队去不去根节点(如果去了,原来的子树可能就没得人了)
对于没有实力到根节点的军队,我们让他们就地驻扎;有实力的军队,我们把它们的剩余时间和来自哪个子树先扔进 选拔集合 里,
现在根的每个子树中已经驻扎的军队都已经标记上了,我们看一看根的每个子树有没有人守的,打上NeedHelp标记
什么样的有实力的军队不能到根节点呢?
如果这个军队跑到根节点,子树没人守了,他却回不去了,肯定是不优的
为什么呢?
对于一个不可以回子树的军队
如果他不跑到根节点,就可以守下这个子树,
如果他跑到根节点,那么必须有一个人帮他守(这个人的剩余价值肯定比他大),然而如果他不跑的话,相当于用一个剩余价值非常小的军队顶上:
V
a
l
u
e
t
h
i
s
T
r
o
o
p
<
V
a
l
u
e
e
d
g
e
<
=
V
a
l
u
e
o
t
h
e
r
T
r
o
o
p
Value_{thisTroop} < Value_{edge} <= Value_{otherTroop}
ValuethisTroop<Valueedge<=ValueotherTroop
那么对于这样的军队,我们让它们 洗洗睡,不要来根节点,同时取消掉这个子树的 NeedHelp 标记
剩下的用排序双指针去跑一个匹配,让实力相匹配的匹配上
最后如果有边匹配不上,那么就需要加大时限,否则就加紧时限
AC-code:
#include <bits/stdc++.h>
using namespace std;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-')
w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
long long rdLL() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-')
w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(long long x) {
static int sta[35];
int f = 1;
if (x < 0)
f = -1, x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if (f == -1)
putchar('-');
while (top)
putchar(sta[--top] + 48);
}
const int N = 3e5 + 5;
int head[N], nxt[N << 1], to[N << 1];
long long val[N << 1], cnt = 0;
void init() {
memset(head, -1, sizeof(head));
cnt = 0;
}
void add(int u, int v, long long w) {
nxt[cnt] = head[u];
to[cnt] = v;
val[cnt] = w;
head[u] = cnt++;
}
int fa[20][N];
long long dis[20][N];
void dfs(int x, int f) {
for (int i = head[x]; ~i; i = nxt[i]) {
int y = to[i], w = val[i];
if (y ^ f) {
dis[0][y] = w;
fa[0][y] = x;
for (int j = 1; j <= 19; j++) {
fa[j][y] = fa[j - 1][fa[j - 1][y]];
dis[j][y] = dis[j - 1][fa[j - 1][y]] + dis[j - 1][y];
}
dfs(y, x);
}
}
}
int t[N], n, m, w[N], rest[N], from[N];
bool vis[N], help[N];
vector<array<long long, 2>> root;
vector<long long> tim, csum;
bool state(int x) {
if (vis[x])
return true;
bool block = true, leaf = true;
for (int i = head[x]; ~i; i = nxt[i]) {
int y = to[i];
if (y ^ fa[0][x]) {
leaf = false;
if (!state(y))
return false;
}
}
if (leaf)
return false;
return block;
}
bool check(long long lim) {
tim.clear();
csum.clear();
root.clear();
memset(vis, 0, sizeof(vis));
memset(help, 0, sizeof(help));
for (int i = 1; i <= m; i++)
w[i] = t[i];
for (int i = 1; i <= m; i++) {
long long k = lim;
for (int j = 19; j >= 0; j--)
if (dis[j][w[i]] <= k && fa[j][w[i]] > 1)
k -= dis[j][w[i]], w[i] = fa[j][w[i]];
if (fa[0][w[i]] == 1 && k >= dis[0][w[i]])
root.emplace_back(array<long long, 2> {w[i], k - dis[0][w[i]]});
else
vis[w[i]] = true;
}
for (int i = head[1]; ~i; i = nxt[i])
if (!state(to[i]))
help[to[i]] = true;
sort(root.begin(), root.end(), [&](array<long long, 2> a, array<long long, 2> b) {
return a[1] > b[1];
});
for (int i = 0; i < root.size(); i++)
if (help[root[i][0]] && root[i][1] < dis[0][root[i][0]])
help[root[i][0]] = false;
else
tim.emplace_back(root[i][1]);
for (int i = head[1]; ~i; i = nxt[i])
if (help[to[i]])
csum.emplace_back(dis[0][to[i]]);
sort(tim.begin(), tim.end());
sort(csum.begin(), csum.end());
int a = tim.size(), b = csum.size();
int i = 0, j = 0;
while (i < a && j < b) {
if (tim[i] >= csum[j])
i++, j++;
else
i++;
}
if (j == b)
return true;
else
return false;
}
signed main() {
init();
n = rd();
for (int i = 1; i < n; i++) {
int u = rd(), v = rd();
long long w = rdLL();
add(u, v, w);
add(v, u, w);
}
m = rd();
for (int i = 1; i <= m; i++)
t[i] = rd();
int tot = 0;
for (int i = head[1]; ~i; i = nxt[i])
tot++;
if (tot > m)
puts("-1"), exit(0);
dfs(1, 0);
long long l = 0, r = 5e14;
while (l < r) {
long long mid = (l + r) >> 1;
if (check(mid))
r = mid;
else
l = mid + 1;
}
wt(r);
return 0;
}
2024/08/09
Phoenix and Bits
合并&分裂 01-Trie
湖北怎么这么喜欢01-Trie啊?
我还没想好怎么写,待补
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
int n,q;
const int N = 2e5+5,U = (1<<20) - 1,M = N * 50;
int cnt,ls[M],rs[M],tagl[M],tagr[M],sum[M],tagx[M],rt;
void push_up(int p) {
tagl[p] = tagl[ls[p]] | tagl[rs[p]];
tagr[p] = tagr[ls[p]] | tagr[rs[p]];
sum[p] = sum[ls[p]] + sum[rs[p]];
}
void push_xor(int p,int x,int dep){
if((x >> dep) & 1) swap(ls[p],rs[p]);
int L = tagl[p],R = tagr[p];
tagl[p] = (L & (x ^ U)) | (R & x);
tagr[p] = (L & x) | (R & (x ^ U));
tagx[p] ^= x;
}
void push_down(int p,int dep) {
if(!tagx[p]) return;
push_xor(ls[p],tagx[p],dep - 1);
push_xor(rs[p],tagx[p],dep - 1);
tagx[p] = 0;
}
void insert(int &p,int x,int dep) {
if(!p) p = ++cnt;
if(dep == -1) {
tagl[p] = x ^ U; // 反 x
tagr[p] = x; // x
sum[p] = 1;
return;
}
(x >> dep) & 1 ? insert(rs[p],x,dep - 1) : insert(ls[p],x,dep - 1);
push_up(p);
}
#define mid ((pl + pr) >> 1)
void split(int &x,int &y,int pl,int pr,int L,int R,int dep) {
if(!x) return;
if(L <= pl && pr <= R) {
y = x,x = 0;
return;
}
push_down(x,dep);
y = ++cnt;
if(L <= mid) split(ls[x],ls[y],pl,mid,L,R,dep - 1);
if(R > mid) split(rs[x],rs[y],mid+1,pr,L,R,dep - 1);
push_up(x),push_up(y);
}
void merge(int &x,int y,int dep) {
if(!x || !y) {x += y;return;}
if(dep == -1) return;
push_down(x,dep);
push_down(y,dep);
merge(ls[x],ls[y],dep - 1);
merge(rs[x],rs[y],dep - 1);
push_up(x);
}
void push_or(int &p,int x,int dep) {
if(dep == -1 || !p) return;
if(!(x & tagl[p] & tagr[p])) {
push_xor(p,x & tagl[p],dep);
return;
}
push_down(p,dep);
if((x >> dep) & 1) {
push_xor(ls[p],1 << dep,dep - 1);
merge(rs[p],ls[p],dep - 1);
ls[p] = 0;
}
push_or(ls[p],x,dep - 1);
push_or(rs[p],x,dep - 1);
push_up(p);
}
#undef mid
signed main() {
n = rd(),q = rd();
for(int i = 1;i<=n;i++) insert(rt,rd(),19);
while(q--) {
int opt = rd(),l = rd(),r = rd(),t,x;
split(rt,t,0,U,l,r,19);
switch(opt) {
case 1:
x = rd();
push_xor(t,U,19);
push_or(t,x ^ U,19);
push_xor(t,U,19);
break;
case 2:
x = rd();
push_or(t,x,19);
break;
case 3:
x = rd();
push_xor(t,x,19);
break;
case 4:
wt(sum[t]);
putchar('\n');
break;
}
merge(rt,t,19);
}
return 0;
}
2024/08/10
CSP-2023
T4 种树
[CSP-S 2023] 种树
题目描述
你是一个森林养护员,有一天,你接到了一个任务:在一片森林内的地块上种树,并养护至树木长到指定的高度。
森林的地图有 n n n 片地块,其中 1 1 1 号地块连接森林的入口。共有 n − 1 n-1 n−1 条道路连接这些地块,使得每片地块都能通过道路互相到达。最开始,每片地块上都没有树木。
你的目标是:在每片地块上均种植一棵树木,并使得 i i i 号地块上的树的高度生长到不低于 a i a_i ai 米。
你每天可以选择一个未种树且与某个已种树的地块直接邻接(即通过单条道路相连)的地块,种一棵高度为 0 0 0 米的树。如果所有地块均已种过树,则你当天不进行任何操作。特别地,第 1 1 1 天你只能在 1 1 1 号空地种树。
对每个地块而言,从该地块被种下树的当天开始,该地块上的树每天都会生长一定的高度。由于气候和土壤条件不同,在第 x x x 天, i i i 号地块上的树会长高 max ( b i + x × c i , 1 ) \max(b_i + x \times c_i, 1) max(bi+x×ci,1) 米。注意这里的 x x x 是从整个任务的第一天,而非种下这棵树的第一天开始计算。
你想知道:最少需要多少天能够完成你的任务?
输入格式
输入的第一行包含一个正整数 n n n,表示森林的地块数量。
接下来 n n n 行:每行包含三个整数 a i , b i , c i a_i, b_i, c_i ai,bi,ci,分别描述一片地块,含义如题目描述中所述。
接下来 n − 1 n-1 n−1 行:每行包含两个正整数 u i , v i u_i, v_i ui,vi,表示一条连接地块 u i u_i ui 和 v i v_i vi 的道路。
输出格式
输出一行仅包含一个正整数,表示完成任务所需的最少天数。
样例 #1
样例输入 #1
4 12 1 1 2 4 -1 10 3 0 7 10 -2 1 2 1 3 3 4样例输出 #1
5提示
【样例 1 解释】
第 1 1 1 天:在地块 1 1 1 种树,地块 1 1 1 的树木长高至 2 2 2 米。
第 2 2 2 天:在地块 3 3 3 种树,地块 1 , 3 1, 3 1,3 的树木分别长高至 5 , 3 5, 3 5,3 米。
第 3 3 3 天:在地块 4 4 4 种树,地块 1 , 3 , 4 1, 3, 4 1,3,4 的树木分别长高至 9 , 6 , 4 9, 6, 4 9,6,4 米。
第 4 4 4 天:在地块 2 2 2 种树,地块 1 , 2 , 3 , 4 1, 2, 3, 4 1,2,3,4 的树木分别长高至 14 , 1 , 9 , 6 14, 1, 9, 6 14,1,9,6 米。
第 5 5 5 天:地块 1 , 2 , 3 , 4 1, 2, 3, 4 1,2,3,4 的树木分别长高至 20 , 2 , 12 , 7 20, 2, 12, 7 20,2,12,7 米。
【样例 2】
见选手目录下的
tree/tree2.in与tree/tree2.ans。【样例 3】
见选手目录下的
tree/tree3.in与tree/tree3.ans。【样例 4】
见选手目录下的
tree/tree4.in与tree/tree4.ans。【数据范围】
对于所有测试数据有: 1 ≤ n ≤ 1 0 5 , 1 ≤ a i ≤ 1 0 18 , 1 ≤ b i ≤ 1 0 9 , 0 ≤ ∣ c i ∣ ≤ 1 0 9 , 1 ≤ u i , v i ≤ n 1 ≤ n ≤ 10^5,1 ≤ a_i ≤ 10^{18}, 1 ≤ b_i ≤ 10^9,0 ≤ |c_i| ≤ 10^9, 1 ≤ u_i, v_i ≤ n 1≤n≤105,1≤ai≤1018,1≤bi≤109,0≤∣ci∣≤109,1≤ui,vi≤n。保证存在方案能在 1 0 9 10^9 109 天内完成任务。
特殊性质 A:对于所有 1 ≤ i ≤ n 1 ≤ i ≤ n 1≤i≤n,均有 c i = 0 c_i = 0 ci=0;
特殊性质 B:对于所有 1 ≤ i < n 1 ≤ i < n 1≤i<n,均有 u i = i u_i = i ui=i、 v i = i + 1 v_i = i + 1 vi=i+1;
特殊性质 C:与任何地块直接相连的道路均不超过 2 2 2 条;
特殊性质 D:对于所有 1 ≤ i < n 1 ≤ i < n 1≤i<n,均有 u i = 1 u_i = 1 ui=1。
很好很好的题,让我万能二分暴毙
看见式子第一件事:拆式子
观察一下增长高度的式子:
max
{
b
i
+
x
c
i
,
1
}
,其中
∣
c
i
∣
∈
[
0
,
1
0
9
]
,
b
i
∈
[
1
,
1
e
9
]
\max{\{ b_i + xc_i,1\}},其中 \lvert c_i \rvert \in [0,10^9], b_i \in [1,1e9]
max{bi+xci,1},其中∣ci∣∈[0,109],bi∈[1,1e9]
那么,我们发现当 c i ≥ 0 c_i \geq 0 ci≥0 时, max { b i + x c i , 1 } = b i + x c i \max{\{ b_i + xc_i,1\}} = b_i + xc_i max{bi+xci,1}=bi+xci
那么分讨一下:
1
◯
c
i
≥
0
\textcircled{1}\ c_i \geq 0
1◯ ci≥0
对于一颗树,树高的增量
Δ
\Delta
Δ 有:
$$
\begin{align*}
\Delta &= \sum_{x = l}^r \max{{ b_i + xc_i,1}} \
&= \sum_{x = l}^r b_i + \sum_{x = l}^r xc_i \
&= (r - l + 1) b_i + \frac{(r - l + 1)(l + r)}{2} c_i
\end{align*} \
l 是种树起始时间,r 是项目终止时间
$$
2
◯
c
i
<
0
\textcircled{2}\ c_i < 0
2◯ ci<0
我们看什么时候,
b
i
+
x
c
i
b_i + xc_i
bi+xci 与
1
1
1 的 大小关系会发生突变
也就是这个式子:
b
i
+
x
c
i
≥
1
⇒
x
≤
1
−
b
i
c
i
b_i + xc_i \geq 1 \ \ \ \Rightarrow \ \ \ x \leq \frac{1 - b_i}{c_i}
bi+xci≥1 ⇒ x≤ci1−bi
因为
x
x
x 有实际意义,
x
∈
Z
x \in Z
x∈Z
那么
x
x
x 最大取值就是
⌊
1
−
b
i
c
i
⌋
\lfloor \frac{1 - b_i}{c_i} \rfloor
⌊ci1−bi⌋,我们记为
k
k
k
那么对于一颗树,树高的增量
Δ
\Delta
Δ 有:
Δ
=
{
r
−
l
+
1
k
<
l
(
r
−
l
+
1
)
b
+
(
l
+
r
)
(
r
−
l
+
1
)
2
c
k
>
r
(
k
−
l
+
1
)
b
+
(
k
−
l
+
1
)
(
l
+
k
)
2
c
+
r
−
k
l
≤
k
≤
r
\Delta = \begin{cases} r-l+1 & & {k < l}\\ (r-l+1)b+\frac{(l+r)(r-l+1)}{2}c & & {k > r} \\ (k - l + 1)b + \frac{(k - l + 1)(l + k)}{2}c + r - k & & {l \leq k \leq r} \\ \end{cases}
Δ=⎩
⎨
⎧r−l+1(r−l+1)b+2(l+r)(r−l+1)c(k−l+1)b+2(k−l+1)(l+k)c+r−kk<lk>rl≤k≤r
这样,我们就可以求出每个点在一段时间内,最晚什么时候种,仍能达到标准(非常重要)
我们看到这种求最少时间的题面,应该第一时间想到二分答案
我们二分最少时间,判断是否能让所有树都达到标准以上
接下来是 c h e c k check check desu
主要的问题是 顺序
我们怎样安排种树顺序来保证种法最优
自然是谁更耗时最长谁先种,
我们处理完每个点的最晚种植时间后,用时间排个序,最晚种植时间越小代表越紧急,放到前面种
因为这个延伸的方式有点想玻璃裂缝
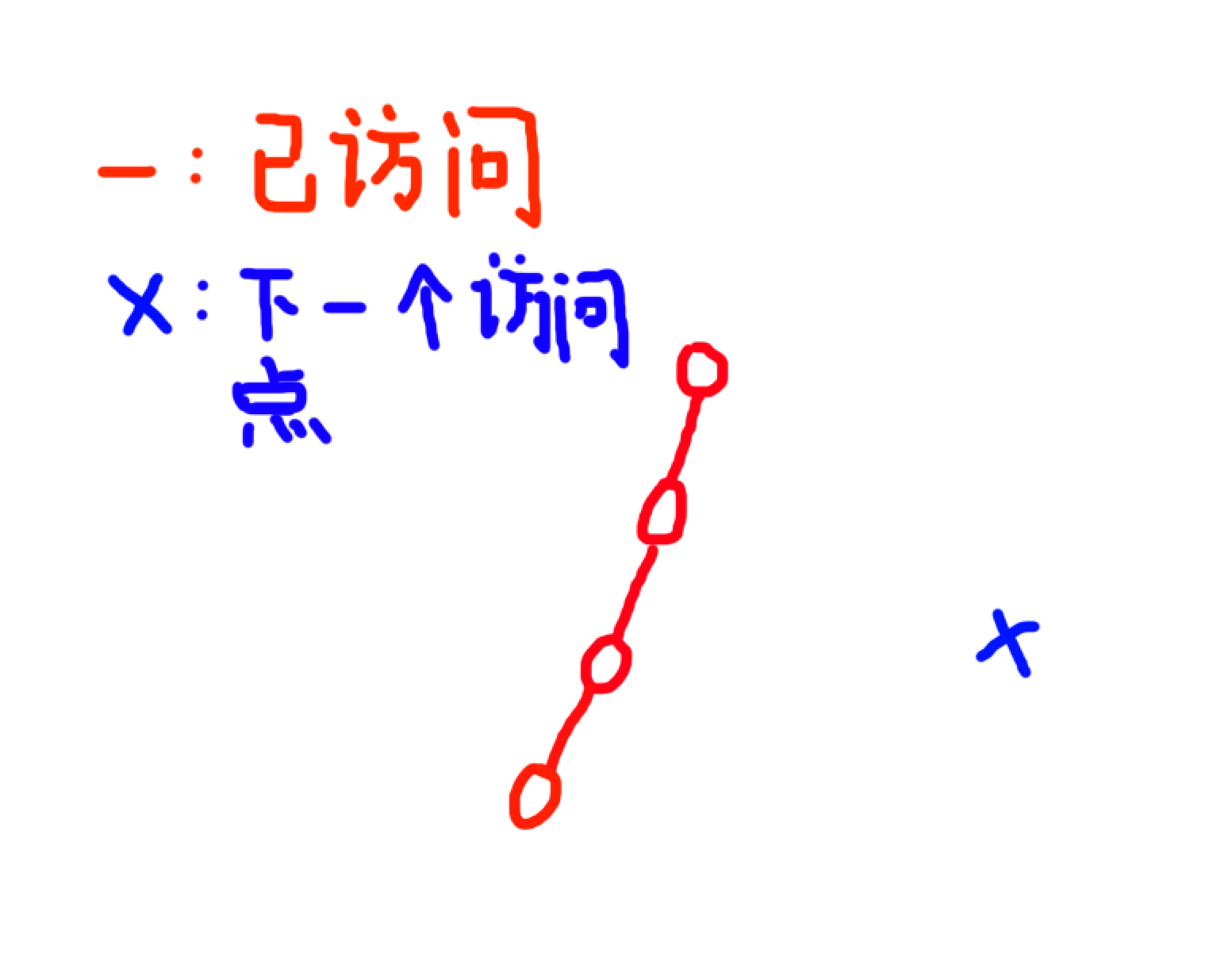
对一个新访问点,我们找路径到 新访问点,并从上到下附上时间戳
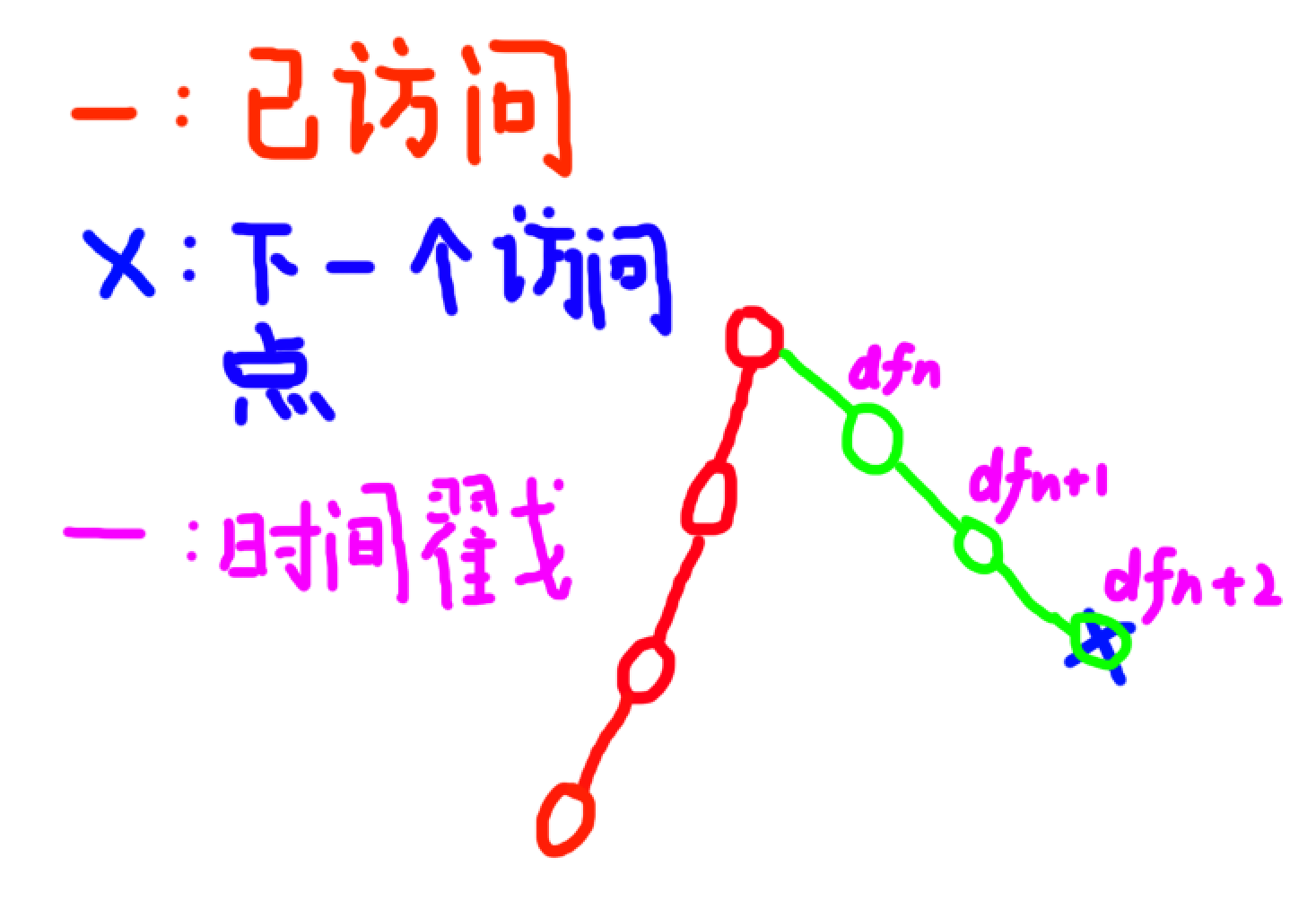
我们可以直接爬父亲,爬到第一个没种树的 k t h kth kth 父亲
然后从它往该点的路径上依次附上种植时间,如果有一个种植时间已经超过最晚种植时间,那么这个方案就失败了(其中 1 1 1 的父亲看作已经种植过)如果每一个都完美种植上,那么就成功了
具体实现:
sort(P + 1,P + n + 1,[&](int ida,int idb){return t[ida] < t[idb];}); // P 是 节点编号, t 是节点对于的最晚种植时间
for(int i = 1,x = 0;i<=n;i++) {
int now = P[i],top = 0;
while(!vis[now]) vis[st[++top] = now] = true,now = fa[now]; // 寻找最远未种植父亲 ,放入栈中(以便附上种植时间),同时打上已种树标记
while(top) if(t[st[top--]] < ++x) return false; // 附上时间戳(种植时间),因为这个时间戳并没有什么用,所以只要判断一下是否合法就可以了
}
return true;
注意一下二分就可以AC了:
时间复杂度
O
(
n
log
n
log
V
)
\mathcal{O}(n\log n \log V)
O(nlognlogV)
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
using int128 = __int128;
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 1e5+5;
int n,head[N],nxt[N<<1],to[N<<1],cnt,fa[N],P[N],t[N],st[N];
bool vis[N];
array<int,3> p[N];
void init() {memset(head,-1,sizeof(head));cnt = 0;}
void add(int u,int v) {
nxt[cnt] = head[u];
to[cnt] = v;
head[u] = cnt++;
}
void dfs(int x,int f) {
fa[x] = f;
for(int i = head[x];~i;i = nxt[i]) {
int y = to[i];
if(y ^ f) dfs(y,x);
}
}
int128 calc(int id,int128 l,int128 r) {
int a = p[id][0],b = p[id][1],c = p[id][2];
if(c >= 0) return (r - l + 1) * b + (r - l + 1) * (r + l) / 2 * c;
int128 k = (1 - b) / c;
if(k < l) return r - l + 1;
else if(k > r) return (r - l + 1) * b + (r - l + 1) * (r + l) / 2 * c;
else return (k - l + 1) * b + (k - l + 1) * (k + l) / 2 * c + r - k;
}
bool check(int tim){
for(int i = 1;i<=n;i++) {
if(calc(i,1,tim) < p[i][0]) return false;
int dl = 1,dr = n;
while(dl < dr) {
int mid = (dr + dl + 1) >> 1;
if(calc(i,mid,tim) >= p[i][0]) dl = mid;
else dr = mid - 1;
}
P[i] = i;t[i] = dl;vis[i] = false;
}
sort(P + 1,P + n + 1,[&](int ida,int idb){return t[ida] < t[idb];});
for(int i = 1,x = 0;i<=n;i++) {
int now = P[i],top = 0;
while(!vis[now]) vis[st[++top] = now] = true,now = fa[now];
while(top) if(t[st[top--]] < ++x) return false;
}
return true;
}
signed main() {
init();
n = rd();
for(int i = 1;i<=n;i++)
p[i][0] = rd(),p[i][1] = rd(),p[i][2] = rd();
for(int i = 1,u,v;i<n;i++)
u = rd(),v = rd(),add(u,v),add(v,u);
dfs(1,0);
vis[0] = true;
int l = n,r = 1e9;
while(l < r - 1) {
int mid = (l + r) >> 1;
if(check(mid)) r = mid;
else l = mid;
}
wt(r);
return 0;
}
梦熊模拟赛MX-X2 T2
给定序列 a a a,
我们要找 a i ≤ ( a i ⊕ a j ) ≤ a j a_i \leq (a_i \oplus a_j) \leq a_j ai≤(ai⊕aj)≤aj 的 ( i , j ) (i,j) (i,j) 二元组对数。
这里提供一个 01 t r i e \textcolor{blue}{01trie} 01trie 做法
首先观察这个条件,因为 a i ≤ a j a_i \leq a_j ai≤aj,所以我们可以钦定一个 a j a_j aj,去找满足条件的 a i a_i ai 的个数。
既然有异或操作,我们可以使用 01 t r i e \textcolor{blue}{01trie} 01trie 来维护每一个值。
不难发现,满足 ( a i ⊕ a j ) ≤ a j (a_i \oplus a_j) \leq a_j (ai⊕aj)≤aj 是 a i ≤ a j a_i \leq a_j ai≤aj 的充分必要条件。
那么,我们考虑 a i ≤ ( a i ⊕ a j ) a_i \leq (a_i \oplus a_j) ai≤(ai⊕aj) 这个条件
我们需要从高位往低位思考,可以得到结论:
a i a_i ai 的最高位低于 a j a_j aj 的最高位。
因为 a i ≤ a j a_i \leq a_j ai≤aj 并且 如果 a i a_i ai 的最高位等于 a j a_j aj 的最高位时, ( a i ⊕ a j ) ≤ min ( a i , a j ) (a_i \oplus a_j) \leq \min(a_i,a_j) (ai⊕aj)≤min(ai,aj)
对于 ( a i ⊕ a j ) (a_i \oplus a_j) (ai⊕aj) 的前 k k k 位与 a j a_j aj 的前 k k k 位相等的 a i a_i ai与 a j a_j aj,如果:
-
a j a_j aj 第 t t t 位为 0 0 0,那么 a i a_i ai 第 t t t 位一定为 0 0 0,不然 ( a i ⊕ a j ) ≥ a j (a_i \oplus a_j) \geq a_j (ai⊕aj)≥aj
例如:
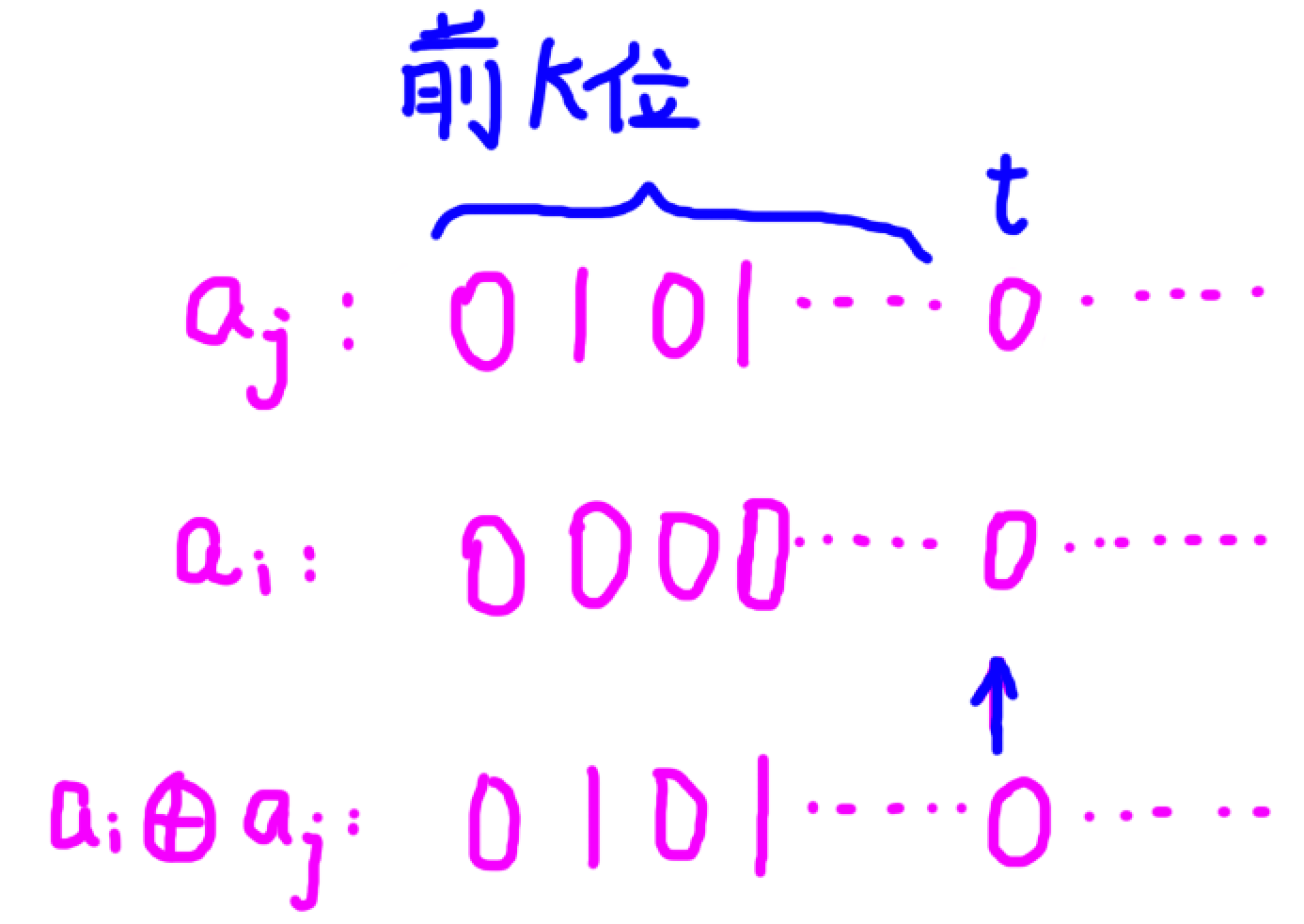
-
a j a_j aj 第 t t t 位为 1 1 1,那么 a i a_i ai 第 t t t 位可以为 1 1 1,此时无论此后然后操作,都可以满足 ( a i ⊕ a j ) ≥ a i (a_i \oplus a_j) \geq a_i (ai⊕aj)≥ai
例如:
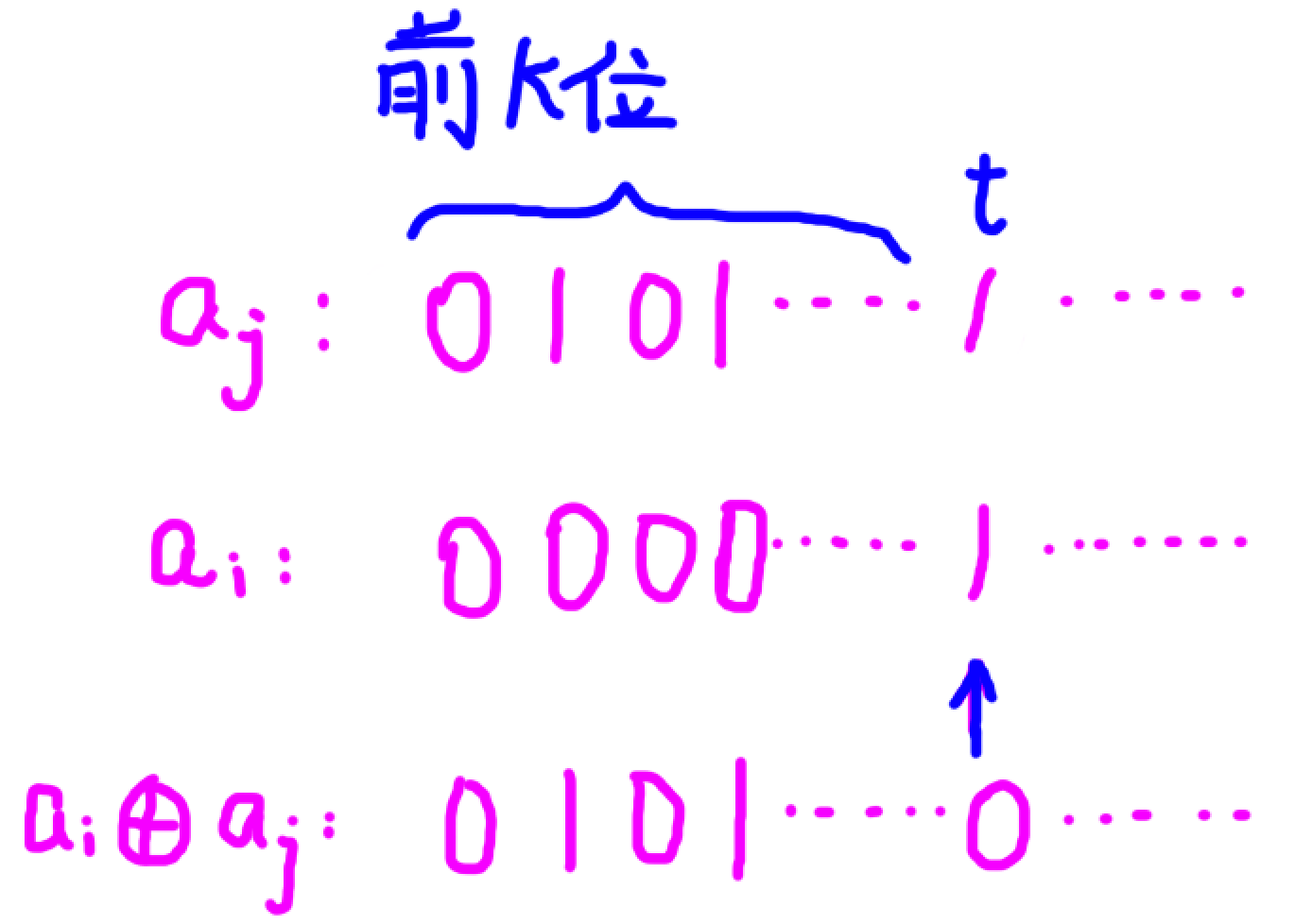
-
a j a_j aj 第 t t t 位为 1 1 1,那么 a i a_i ai 第 t t t 位可以为 0 0 0,此时需要再往后重复上述判断,直到每一位判断完
例如:
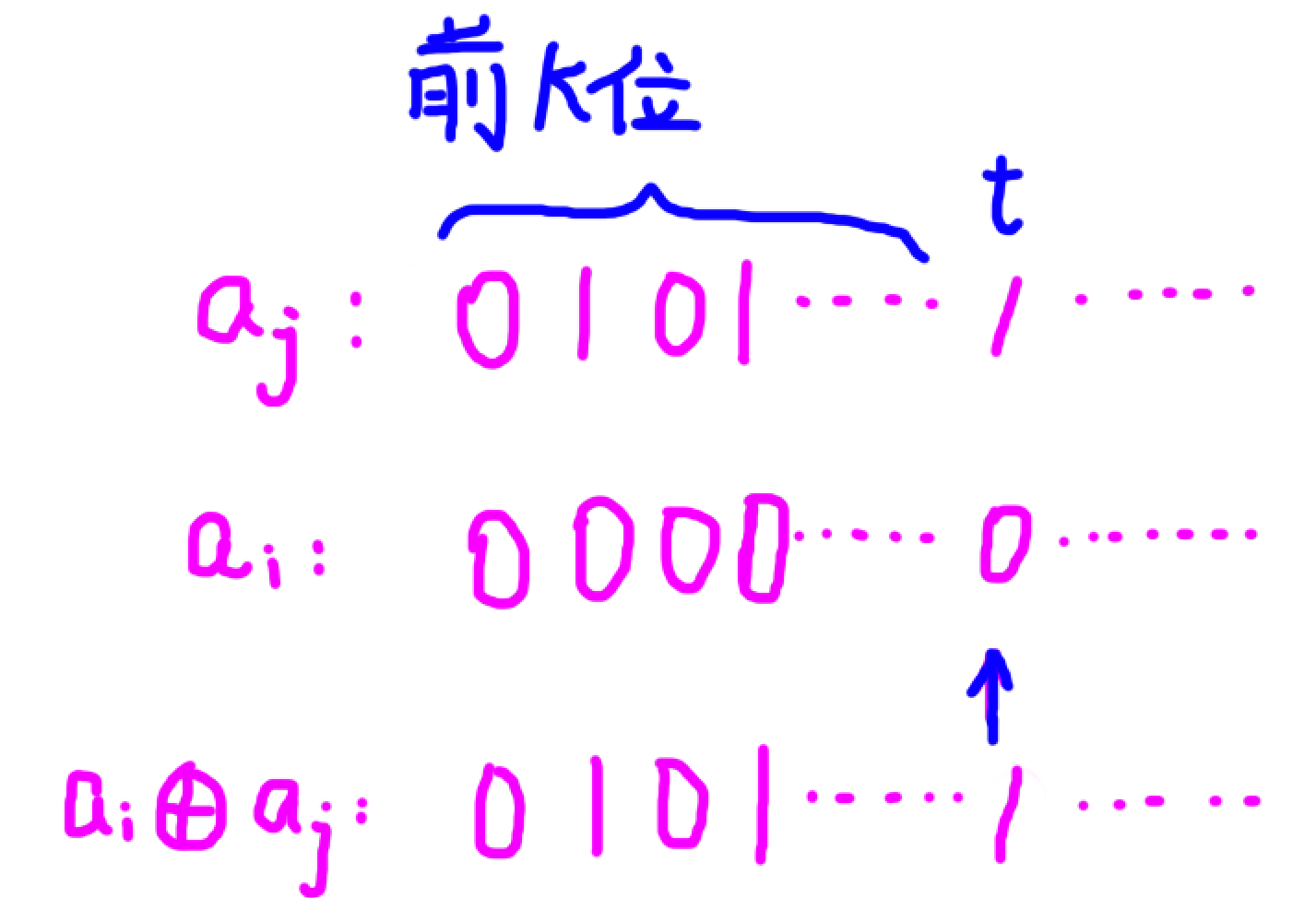
那么建出 01 t r i e \textcolor{blue}{01trie} 01trie,类似于动态开点线段树,依照上述方法在这个 01 t r i e \textcolor{blue}{01trie} 01trie 上统计答案即可
时间复杂度: O ( ∑ n log V ) \mathcal{O}(\sum n\log V) O(∑nlogV)
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 5e5 + 5;
int rt,ls[N * 30],rs[N * 30],sum[N * 30],cnt;
void push_up(int p) {
sum[p] = sum[ls[p]] + sum[rs[p]];
}
void ins(int &p,int x,int dep) {
if(!p) p = ++cnt;
if(dep == -1) {
sum[p]++;
return;
}
(x >> dep) & 1 ? ins(rs[p],x,dep - 1) : ins(ls[p],x,dep - 1);
push_up(p);
}
int Find(int &p,int x,int dep,bool flag) {
if(!p) return 0;
if(dep == -1) return sum[p];
int res = 0;
if((x >> dep) & 1) {
if(flag) {
res += Find(ls[p],x,dep - 1,true);
res += sum[rs[p]];
}else
res += Find(ls[p],x,dep - 1,true);
}else res += Find(ls[p],x,dep - 1,flag);
return res;
}
void init() {
for(int i = 0;i<=cnt;i++) ls[i] = rs[i] = sum[i] = 0;
cnt = 0;
rt = 0;
}
void solve() {
int n = rd();
vector<int> a(n);
int ans = 0;
init();
for(int i = 0;i<n;i++) a[i] = rd();
for(int i = 0;i<n;i++) ins(rt,a[i],29);
for(int i = 0;i<n;i++)
ans += Find(rt,a[i],29,false);
wt(ans);
putchar('\n');
}
signed main() {
int T = rd();
while(T--) solve();
return 0;
}






















 343
343

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








