2024.7 - 做题记录与方法总结-Part3

最新推荐文章于 2024-08-21 17:24:53 发布
最新推荐文章于 2024-08-21 17:24:53 发布
阅读量531 收藏 9
点赞数 8
分类专栏： 做题记录与方法总结 文章标签： 算法 c++ 笔记 其他
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_49785217/article/details/141390631
版权

2024/07/15

进入培训阶段

先写个 A C AC AC 自动机（简单版）

P3808 AC 自动机（简单版）

题面：

AC 自动机（简单版）
题目描述

给定 n n n 个模式串 s i s_i si​ 和一个文本串 t t t，求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。

输入格式

第一行是一个整数，表示模式串的个数 n n n。
第 2 2 2 到第 ( n + 1 ) (n + 1) (n+1) 行，每行一个字符串，第 ( i + 1 ) (i + 1) (i+1) 行的字符串表示编号为 i i i 的模式串 s i s_i si​。
最后一行是一个字符串，表示文本串 t t t。

输出格式

输出一行一个整数表示答案。

样例 #1
样例输入 #1
3
a
aa
aa
aaa
样例输出 #1
3
样例 #2
样例输入 #2
4
a
ab
ac
abc
abcd
样例输出 #2
3
样例 #3
样例输入 #3
2
a
aa
aa
样例输出 #3
2
提示
样例 1 解释

s 2 s_2 s2​ 与 s 3 s_3 s3​ 编号（下标）不同，因此各自对答案产生了一次贡献。

样例 2 解释

s 1 s_1 s1​， s 2 s_2 s2​， s 4 s_4 s4​ 都在串 abcd 里出现过。

数据规模与约定
  • 对于 50 % 50\% 50% 的数据，保证 n = 1 n = 1 n=1。
  • 对于 100 % 100\% 100% 的数据，保证 1 ≤ n ≤ 1 0 6 1 \leq n \leq 10^6 1≤n≤106， 1 ≤ ∣ t ∣ ≤ 1 0 6 1 \leq |t| \leq 10^6 1≤∣t∣≤106， 1 ≤ ∑ i = 1 n ∣ s i ∣ ≤ 1 0 6 1 \leq \sum\limits_{i = 1}^n |s_i| \leq 10^6 1≤i=1∑n​∣si​∣≤106。 s i , t s_i, t si​,t 中仅包含小写字母。

KMP对于多个模式串无能为力，那么AC自动机就出现了

首先是字典树插入

void insert(char *s) {
	int p = 0;
	for(int i = 0;s[i];i++) {
		int j = s[i] - 'a';
		if(!ch[p][j]) ch[p][j] = ++idx;
		p = ch[p][j];
	}
	cnt[p]++;
}

然后是建立AC自动机

void build() {
	queue<int> q;
	for(int i = 0;i<26;i++) 
		if(ch[0][i]) q.push(ch[0][i]);
	while(!q.empty()) {
		int u = q.front();
		q.pop();
		for(int i = 0;i<26;i++) {
			int v = ch[u][i];
			if(v) nxt[v] = ch[nxt[u]][i],q.push(v); // 这里是建回跳链，主要是看后缀
			else ch[u][i] = ch[nxt[u]][i];// 这里是转移链，匹配其他串
		}
	}
}

最后查询：

int query(char *s) {
	int ans = 0;
	for(int k = 0,i = 0;s[k];k++) {
		i = ch[i][s[k] - 'a'];//走串
		for(int j = i;j && ~cnt[j];j = nxt[j])//跳链，判断是否回到 0 节点/ 串是否已经被访问
			ans += cnt[j],cnt[j] = -1;//累加结果，然后打上标记，表示此串已经被访问
	}
	return ans;
}

AC-code:

#include<bits/stdc++.h>
using namespace std;

const int N = 1e6 + 5;

int ch[N][26],nxt[N],cnt[N],idx;

void insert(char *s) {
	int p = 0;
	for(int i = 0;s[i];i++) {
		int j = s[i] - 'a';
		if(!ch[p][j]) ch[p][j] = ++idx;
		p = ch[p][j];
	}
	cnt[p]++;
}

void build() {
	queue<int> q;
	for(int i = 0;i<26;i++) 
		if(ch[0][i]) q.push(ch[0][i]);
	while(!q.empty()) {
		int u = q.front();
		q.pop();
		for(int i = 0;i<26;i++) {
			int v = ch[u][i];
			if(v) nxt[v] = ch[nxt[u]][i],q.push(v);
			else ch[u][i] = ch[nxt[u]][i];
		}
	}
}

int query(char *s) {
	int ans = 0;
	for(int k = 0,i = 0;s[k];k++) {
		i = ch[i][s[k] - 'a'];
		for(int j = i;j && ~cnt[j];j = nxt[j])
			ans += cnt[j],cnt[j] = -1;
	}
	return ans;
}

int n;
char s[N],t[N];

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	
	cin>>n;
	for(int i = 1;i<=n;i++) {
		cin>>s;
		insert(s);
	}
	cin>>t;
	build();
	cout<<query(t);

	return 0;
}

2024/07/17

LEGOndary Grandmaster

题面：

题面翻译

对于两个长度为 n n n 的 01 01 01 串 s , t s,t s,t ，你可以对 s s s 进行两种操作：把相邻两个 0 0 0 变成 1 1 1 或把相邻两个 1 1 1 变成 0 0 0 ，定义 s s s 到 t t t 的距离为最少操作次数使得 s s s 变成 t t t ，如过没法变则距离为 0 0 0 。

现在你有两个不完整的字符串，可以把其中的 ? ? ? 变成 0 0 0 或 1 1 1 ，求所有情况所得到的两个 01 01 01 串的距离之和。

有趣的结论：
00 → 11 , 11 → 00 ⇒ 在偶数位取反 10 → 01 , 01 → 10 ，即‘交换’ 00 \rightarrow 11 , 11 \rightarrow 00 \Rightarrow^{在偶数位取反} 10 \rightarrow 01,01 \rightarrow 10，即 ‘交换’ 00→11,11→00⇒在偶数位取反10→01,01→10，即‘交换’

最小步数： ∑ i ∣ a i − b i ∣ \sum_i \lvert a_i - b_i \rvert ∑i​∣ai​−bi​∣

待补！

最近唐完了，发生了各种各样的意外。

因为在集训，没来的及在 NOI之前给 ckain 送祝福

所以在这里，我祝 ckain 学长能在 NOI 赛场上叱诧风云，做一个风云人物 ！

愿上天保佑你

P2668 [NOIP2015 提高组] 斗地主

大模拟，唯一关键的点在于：只剩下 炸弹，对子，单张，只需要一次就可以打完，所以最后判断该数码是否还有牌，有牌就加1，否则跳过

其他都是细节

AC-code:

#include<bits/stdc++.h>
using namespace std;

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

int n,t[20],ans = 0x3f3f3f3f;

void dfs(int dep){
	if(dep >= ans) return;
	int k = 0;
	for(int i = 3;i<=14;i++) {
		if(t[i] == 0) k = 0;
		else {
			k++;
			if(k >= 5) {
				int l = i - k + 1;
				for(int j = l;j<=i;j++) t[j]--;
				dfs(dep + 1);
				for(int j = l;j<=i;j++) t[j]++;
			}
		}
	}
	k = 0;
	for(int i = 3;i<=14;i++){
		if(t[i] <= 1) k = 0;
		else {
			k++;
			if(k >= 3) {
				int l = i - k + 1;
				for(int j = l;j<=i;j++) t[j] -= 2;
				dfs(dep + 1);
				for(int j = l;j<=i;j++) t[j] += 2;
			}
		}
	}
	k = 0;
	for(int i = 3;i<=14;i++) {
		if(t[i] <= 2) k = 0;
		else {
			k++;
			if(k >= 2) {
				int l = i - k + 1;
				for(int j = l;j<=i;j++) t[j] -= 3;
				dfs(dep + 1);
				for(int j = l;j<=i;j++) t[j] += 3;
			}
		}
	}

	for(int i = 3;i<=15;i++) {
		if(t[i] <= 3) {
			if(t[i] < 3) continue;
			t[i] -= 3;
			for(int j = 0;j<=15;j++) {
				if(i == j || j == 1 || j == 2 || t[j] == 0) continue;
				t[j]--;
				dfs(dep + 1);
				t[j]++;
			}
			for(int j = 3;j<=15;j++) {
				if(i == j || t[j]  <= 1) continue;
				t[j] -= 2;
				dfs(dep + 1);
				t[j] += 2;
			}
			t[i] += 3;
		}else {
			t[i] -= 3;
			for(int j = 3;j<=15;j++) {
				if(i == j || t[j] == 0) continue;
				t[j]--;
				dfs(dep + 1);
				t[j]++;
			}
			for(int j = 3;j<=15;j++) {
				if(i == j || t[j]  <= 1) continue;
				t[j] -= 2;
				dfs(dep + 1);
				t[j] += 2;
			}
			t[i] += 3;

			t[i] -= 4;
			for(int j = 0;j<=15;j++) {
				if(t[j] == 0 || j == 1 || j == 2 || j == i) continue;
				t[j]--;
				for(int k = 0;k<=15;k++) {
					if(t[k] == 0 || k == 1 || k == 2 || k == j) continue;
					t[k]--;
					dfs(dep + 1);
					t[k]++;
				}
				t[j]++;
			}
			for(int j = 3;j<=15;j++) {
				if(t[j] <= 1) continue;
				t[j] -= 2;
				for(int k = 3;k<=15;k++){
					if(t[k] <= 1) continue;
					t[k] -= 2;
					dfs(dep + 1);
					t[k] += 2;
				}
				t[j] += 2;
			}
			t[i] += 4;
		}
	}
	int res = dep;
	for(int i = 0;i<=15;i++) {
		if(i == 1 || i == 2) continue;
		res += (t[i]) ? 1:0;
	}
	ans = min(res,ans);
}

void solve() {
	memset(t,0,sizeof(t));
	ans = 0x3f3f3f3f;
    for(int i = 1;i<=n;i++) t[rd()]++,rd();
	t[1 + 13] = t[1];
	t[2 + 13] = t[2];
	t[1] = t[2] = 0;
	dfs(0);
	wt(ans);putchar('\n');
}

signed main() {
    int T;
	T = rd(),n = rd();
    while(T--) solve(); 

	return 0;
}

P2668 [NOIP2015 提高组] 斗地主 加强版

同上，但是上面的代码有瑕疵

  1. 四带二，没说就是同类也可以带，如：4444 带 22 和 22
  2. 超时了！怎么办 -> 记忆化，直接用 unordered_map hash 局面，我们发现花色啥用没有，我们只关心每种牌的数量，所以我们可以压到一个字符串里，记录这个串到清牌需要几步,(初始化为 inf,且在使用时判断是否 < inf)

做好这两步，本题就解决了
AC-code:

#include<bits/stdc++.h>
using namespace std;

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

int n,t[20],ans = 0x3f3f3f3f,inf = 0x3f3f3f3f;

unordered_map<string,int> f;

int dfs(int dep){
	if(dep >= ans) return inf;

	string s;
	for(int i = 0;i<=15;i++) s.push_back(t[i] + '0');
	if(f.count(s) && f[s] != inf) {
		ans = min(ans,f[s] + dep);
		return f[s] + dep;
	}else f[s] = inf;
	int k = 0;
	for(int i = 3;i<=14;i++) {
		if(t[i] == 0) k = 0;
		else {
			k++;
			if(k >= 5) {
				int l = i - k + 1;
				for(int j = l;j<=i;j++) t[j]--;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				for(int j = l;j<=i;j++) t[j]++;
			}
		}
	}
	k = 0;
	for(int i = 3;i<=14;i++){
		if(t[i] <= 1) k = 0;
		else {
			k++;
			if(k >= 3) {
				int l = i - k + 1;
				for(int j = l;j<=i;j++) t[j] -= 2;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				for(int j = l;j<=i;j++) t[j] += 2;
			}
		}
	}
	k = 0;
	for(int i = 3;i<=14;i++) {
		if(t[i] <= 2) k = 0;
		else {
			k++;
			if(k >= 2) {
				int l = i - k + 1;
				for(int j = l;j<=i;j++) t[j] -= 3;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				for(int j = l;j<=i;j++) t[j] += 3;
			}
		}
	}

	for(int i = 3;i<=15;i++) {
		if(t[i] <= 3) {
			if(t[i] < 3) continue;
			t[i] -= 3;
			for(int j = 0;j<=15;j++) {
				if(i == j || j == 1 || j == 2 || t[j] == 0) continue;
				t[j]--;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				t[j]++;
			}
			for(int j = 3;j<=15;j++) {
				if(i == j || t[j]  <= 1) continue;
				t[j] -= 2;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				t[j] += 2;
			}
			t[i] += 3;
		}else {
			t[i] -= 3;
			for(int j = 3;j<=15;j++) {
				if(i == j || t[j] == 0) continue;
				t[j]--;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				t[j]++;
			}
			for(int j = 3;j<=15;j++) {
				if(i == j || t[j]  <= 1) continue;
				t[j] -= 2;
				f[s] = min(f[s],dfs(dep + 1) - dep);
				t[j] += 2;
			}
			t[i] += 3;

			t[i] -= 4;
			for(int j = 0;j<=15;j++) {
				if(t[j] == 0 || j == 1 || j == 2 || j == i) continue;
				t[j]--;
				for(int k = 0;k<=15;k++) {
					if(t[k] == 0 || k == 1 || k == 2) continue;
					t[k]--;
					f[s] = min(f[s],dfs(dep + 1) - dep);
					t[k]++;
				}
				t[j]++;
			}
			for(int j = 3;j<=15;j++) {
				if(t[j] <= 1) continue;
				t[j] -= 2;
				for(int k = 3;k<=15;k++){
					if(t[k] <= 1) continue;
					t[k] -= 2;
					f[s] = min(f[s],dfs(dep + 1) - dep);
					t[k] += 2;
				}
				t[j] += 2;
			}
			t[i] += 4;
		}
	}
	int res = dep;
	for(int i = 0;i<=15;i++) {
		if(i == 1 || i == 2) continue;
		res += (t[i]) ? 1:0;
	}
	ans = min(res,ans);
	return res;
}

void solve() {
	memset(t,0,sizeof(t));
	f.clear();
	ans = 0x3f3f3f3f;
    for(int i = 1;i<=n;i++) t[rd()]++,rd();
	t[1 + 13] = t[1];
	t[2 + 13] = t[2];
	t[1] = t[2] = 0;
	dfs(0);
	wt(ans);putchar('\n');
}

signed main() {
    int T;
	T = rd(),n = rd();
    while(T--) solve(); 

	return 0;
}

2024/07/19

Polo the Penguin and Trees

题面：

题面翻译

题意：给定 n n n 个节点的树，求满足条件的四元组 ( a , b , c , d ) (a,b,c,d) (a,b,c,d) 的数量：

  • 1 ≤ a < b ≤ n 1 ≤ c < d ≤ n 1\leq a< b\leq n\quad 1\leq c< d\leq n 1≤a<b≤n1≤c<d≤n

  • a a a 到 b b b 和 c c c 到 d d d 的路径没有交点

n ≤ 8 × 1 0 4 n\leq 8\times 10^4 n≤8×104

样例 #1
样例输入 #1
4
1 2
2 3
3 4
样例输出 #1
2

还是 正难则反 的思想

所有的四元对有 ( n 2 ) 2 \dbinom{n}{2}^2 (2n​)2 种

那么我们考虑相交的方案

首先，我们考虑两条路径不在一颗子树的方案

那么这两条路径在哪交呢？

我们钦定 p p p 节点为两条路径的交

那么在 p p p 子树内经过 p p p 的线段有 ( s i z p 2 ) − ∑ q ∈ s o n p ( s i z q 2 ) \dbinom{siz_p}{2} - \sum_{q \in son_p}\dbinom{siz_q}{2} (2sizp​​)−∑q∈sonp​​(2sizq​​)

不在 p p p 子树的结点有 n − s i z p n - siz_p n−sizp​ 个

那么经过 p p p 节点但不在 p p p 子树内的线段有 ( n − s i z p ) s i z p (n - siz_p)siz_p (n−sizp​)sizp​ 个

那么两条路径都在 p p p 的四元对有 a = ( ( s i z p 2 ) − ∑ q ∈ s o n p ( s i z q 2 ) ) 2 a = (\dbinom{siz_p}{2} - \sum_{q \in son_p}\dbinom{siz_q}{2}) ^ 2 a=((2sizp​​)−∑q∈sonp​​(2sizq​​))2

两条路径不在同一子树上的四元对有 b = 2 ( s i z p ( n − s i z p ) ( ( s i z p 2 ) − ∑ q ∈ s o n p ( s i z q 2 ) ) ) b = 2(siz_p(n - siz_p)(\dbinom{siz_p}{2} - \sum_{q \in son_p}\dbinom{siz_q}{2})) b=2(sizp​(n−sizp​)((2sizp​​)−∑q∈sonp​​(2sizq​​)))

最后的答案为 $ \dbinom{n}{2}^2 - a - b$

AC-code:


#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 80005;

int n,head[N],nxt[N<<1],to[N<<1],cnt;

void init() {memset(head,-1,sizeof(head));}

void add(int u,int v) {
    nxt[cnt] = head[u];
    to[cnt] = v;
    head[u] = cnt++;
}

int siz[N],fa[N],del;

void dfs1(int x,int f) {
    siz[x] = 1;
    fa[x] = f;
    for(int i = head[x];~i;i = nxt[i]) {
        int y = to[i];
        if(y ^ f) {
            dfs1(y,x);
            siz[x] += siz[y];
        }
    }
}

int C2(int x) {
	if(x < 0) return 0;
	return x * (x - 1) / 2;
}

void dfs2(int x) {
    int ans1 = C2(siz[x]),ans2 = (n - siz[x]) * siz[x];
    for(int i = head[x];~i;i = nxt[i]) {
        int y = to[i];
        if(y ^ fa[x]) {
            dfs2(y);
            ans1 -= C2(siz[y]); 
        }
    }
    del += ans1 * ans2 * 2 + ans1 * ans1;
}

// 正难则反

signed main() {
    init();
	n = rd();
    for(int i = 1,u,v;i<n;i++) {
        u = rd(),v = rd();
        add(u,v);add(v,u);
    }
    int k = 0;
    dfs1(1,0);
    dfs2(1);
    wt(C2(n) * C2(n) - del);

	return 0;
}

The Bakery

题面：

题面翻译

将一个长度为 n n n 的序列分为 k k k 段，使得总价值最大。

一段区间的价值表示为区间内不同数字的个数。

n ≤ 35000 , k ≤ 50 n\leq 35000,k\leq 50 n≤35000,k≤50

Translated by @ysner @yybyyb

样例 #1
样例输入 #1
4 1
1 2 2 1
样例输出 #1
2
样例 #2
样例输入 #2
7 2
1 3 3 1 4 4 4
样例输出 #2
5
样例 #3
样例输入 #3
8 3
7 7 8 7 7 8 1 7
样例输出 #3
6

线段树优化的典题，但是我们要用四边形不等式

以此为四边形不等式优化dp的模板

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 35005;

int L = 1,R,ans,cnt[N];

int n,k;
int f[N][51],a[N];

void add(int x) {
	if(!cnt[x]) ans++;
	cnt[x]++;
}
void del(int x) {
	cnt[x]--;
	if(!cnt[x]) ans--;
}

int val(int l,int r) {
    while(L > l) add(a[--L]);
    while(R < r) add(a[++R]);
    while(R > r) del(a[R--]);
    while(L < l) del(a[L++]);
    return ans;
}

void solve(int pl,int pr,int l,int r,int tot) {
    if(pl > pr) return;
    int mid = (pl + pr) >> 1,qmid = l;
    for(int i = l;i <= min(r,mid);i++) {
        int las = f[i - 1][tot - 1] + val(i,mid);
        bool update = las > f[mid][tot];
        if(update) f[mid][tot] = las,qmid = i;//找最优分割点
    }
    solve(pl,mid - 1,l,qmid,tot);
    solve(mid + 1,pr,qmid,r,tot);
}

signed main() {
	n = rd(),k = rd();
    for(int i = 1;i<=n;i++) a[i] = rd();
    memset(f,0xcf,sizeof(f));
    f[0][0] = 0;
    for(int i = 1;i<=k;i++) solve(1,n,1,n,i);
    wt(f[n][k]);
	return 0;
}

什么情况满足四边形不等式呢？

来自梦熊联盟课件

考虑如下问题： f ( i ) = min ⁡ 1 ≤ j ≤ i w ( j , i ) f(i)=\min_{1\leq j\leq i}w(j,i) f(i)=min1≤j≤i​w(j,i)。

如果对任意 a , b , c , d ( a ≤ b ≤ c ≤ d ) a,b,c,d(a\leq b\leq c\leq d) a,b,c,d(a≤b≤c≤d) 满足 w ( a , c ) + w ( b , d ) ≤ w ( a , d ) + w ( b , c ) w(a,c)+w(b,d)\leq w(a,d)+w(b,c) w(a,c)+w(b,d)≤w(a,d)+w(b,c)，则称 w w w 满足四边形不等式。

哪些满足四边形不等式？

  1. 如果 w ( j , i ) w(j,i) w(j,i) 满足四边形不等式，那么 w ′ ( j , i ) = f ( j − 1 ) + w ( j , i ) w'(j,i)=f(j-1)+w(j,i) w′(j,i)=f(j−1)+w(j,i) 也满足四边形不等式。
    w ( a , c ) + w ( b , d ) ≤ w ( a , d ) + w ( b , c ) f ( a − 1 ) + f ( b − 1 ) + w ( a , c ) + w ( b , d ) ≤ f ( a − 1 ) + f ( b − 1 ) + w ( a , d ) + w ( b , c ) ( f ( a − 1 ) + w ( a , c ) ) + ( f ( b − 1 ) + w ( b , d ) ) ≤ ( f ( a − 1 ) + w ( a , d ) ) + ( f ( b − 1 ) + w ( b , c ) ) \begin{aligned} w(a,c)+w(b,d)&\leq w(a,d)+w(b,c)\\ f(a-1)+f(b-1)+w(a,c)+w(b,d)&\leq f(a-1)+f(b-1)+w(a,d)+w(b,c)\\ (f(a-1)+w(a,c))+(f(b-1)+w(b,d))&\leq (f(a-1)+w(a,d))+(f(b-1)+w(b,c))\\ \end{aligned} w(a,c)+w(b,d)f(a−1)+f(b−1)+w(a,c)+w(b,d)(f(a−1)+w(a,c))+(f(b−1)+w(b,d))​≤w(a,d)+w(b,c)≤f(a−1)+f(b−1)+w(a,d)+w(b,c)≤(f(a−1)+w(a,d))+(f(b−1)+w(b,c))​
    f ( i ) = min ⁡ 1 ≤ j ≤ i f ( j − 1 ) + w ( j , i ) f(i)=\min_{1\leq j\leq i}f(j-1)+w(j,i) f(i)=min1≤j≤i​f(j−1)+w(j,i)。

  2. w ( j , i ) = v j w(j,i)=v_j w(j,i)=vj​。
    w ( a , c ) + w ( b , d ) ≤ w ( a , d ) + w ( b , c ) v a + v b ≤ v a + v b w(a,c)+w(b,d)\leq w(a,d)+w(b,c)\\ v_a+v_b\leq v_a+v_b w(a,c)+w(b,d)≤w(a,d)+w(b,c)va​+vb​≤va​+vb​

  3. w ( j , i ) = v i w(j,i)=v_i w(j,i)=vi​。

  4. w ( j , i ) = j i w(j,i)=ji w(j,i)=ji。
    w ( a , c ) + w ( b , d ) ≥ w ( a , d ) + w ( b , c ) a c + b d ≥ a d + b c b ( d − c ) ≥ a ( d − c ) b ≥ a w(a,c)+w(b,d)\geq w(a,d)+w(b,c)\\ ac+bd\geq ad+bc\\ b(d-c)\geq a(d-c)\\ b\geq a w(a,c)+w(b,d)≥w(a,d)+w(b,c)ac+bd≥ad+bcb(d−c)≥a(d−c)b≥a

  5. w ( j , i ) = ( i − j ) p w(j,i)=(i-j)^p w(j,i)=(i−j)p， p ≥ 1 p\geq 1 p≥1。

    证明要用到微积分知识，略去。

  6. 有另一个非负数组 v v v，且 w ( j , i ) = ∑ j ≤ l ≤ r ≤ i v ( l , r ) w(j,i)=\sum_{j\leq l\leq r\leq i}v(l,r) w(j,i)=∑j≤l≤r≤i​v(l,r)。

  7. w ( j , i ) = h ( i − j ) w(j,i)=h(i-j) w(j,i)=h(i−j)， h h h 是下凸函数。

2024/07/20

mx_模拟赛

唐完了

D.几何题（triangle）
题目描述

在小学的课堂上，你学会了如何判断三条边是否能组成一个三角形：若三条边长为 x,y,z ，如果 x+y>z,x+z>y,y+z>x 均成立，它们就能组成一个周长为 x+y+z 的三角形。

现在有 n 根木棍，第 i 根的长度是 a_i ，你需要支持 q 次操作：

  • 0 p v，令 a_p=v 。
  • 1 l r，询问如果仅使用第 l,l+1,\dots,r 根木棍中的三根来组成三角形，且每条边恰由一根木棍组成，你能得到的三角形周长最大是多少。如果不能构成三角形，则回答 0 。

少些一个 ‘=’ ，少了 95 95 95 分，警钟长鸣

首先，我们来看一看组成三角形的条件：
a + b ≤ c a + b \leq c a+b≤c

那么，如何在众多数中找出周长最大的合法三角形呢?

我们考虑贪心，对数进行从大到小排序：

不难看出：
对于连续的 3 个数—— i , j , k ( i + 2 = j + 1 = k ) 如果 a i + a j ≤ a k 那么对于 p , q ≤ j , a p + a q ≤ a i + a j ≤ a k ，即 a p + a q 绝对不优 对于连续的 3 个数 —— i,j,k (i + 2 = j + 1 = k) \\ 如果 a_i + a_j \leq a_k \\ 那么对于 p,q \leq j, a_p + a_q \leq a_i + a_j \leq a_k，即 a_p + a_q 绝对不优 对于连续的3个数——i,j,k(i+2=j+1=k)如果ai​+aj​≤ak​那么对于p,q≤j,ap​+aq​≤ai​+aj​≤ak​，即ap​+aq​绝对不优

那么，我们只需要用一个 连续三元组[i,j,k]滑动窗口计算就可以了，时间复杂度 O ( n ) O(n) O(n)

对于连续四元组 [ a , b , c ] ，假如 a + b ≤ c ⋀ a ≤ b 那么 a ≤ c 2 对于连续四元组 [a,b,c]，假如 \\ a + b \leq c \bigwedge a \leq b \\ 那么 a \leq \frac{c}{2} 对于连续四元组[a,b,c]，假如a+b≤c⋀a≤b那么a≤2c​

简单来说,对于一列数，如果这一列数 ( l e n ≥ 2 ) (len \geq 2) (len≥2) 不能构成任何三角形，不连续序列数的数量为 O ( l o g 2 n ) O(log_2n) O(log2​n)

接下来是套路，我们要存多少数呢？ l o g 2 ( 5 × 1 0 8 ) ≈ 30 log_2 (5\times 10 ^ 8) \approx 30 log2​(5×108)≈30

如果读者写过 P5478，这题就变成了弟中之弟

现在问题就很明晰了（我在赛场上不到 10 10 10 min 就想到了）

用线段树维护区间前 30 30 30 个数， p u s h _ u p push\_ up push_up 用归并排序上传

可惜赛时细节直接来了一次暴扣

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 2e5+5;
int A[N];

namespace sgt{

#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

struct node{
	int r[30],len;
	node(){memset(r,0,sizeof(r));}
}t[N<<2];

node merge(node a,node b){
	node c;
	c.len = 0;
	int i = 1,j = 1;
	while(i <= a.len && j <= b.len && c.len < 29) {
		if(a.r[i] > b.r[j]) c.r[++c.len] = a.r[i++];
		else c.r[++c.len] = b.r[j++];
	}
	while(i <= a.len && c.len < 29) c.r[++c.len] = a.r[i++];
	while(j <= b.len && c.len < 29) c.r[++c.len] = b.r[j++];
	return c;
}

void push_up(int p) {
    t[p] = merge(t[ls],t[rs]);
}

void build(int p,int pl,int pr) {
    if(pl == pr) {
    	t[p].r[1] = A[pl];
        t[p].len = 1;
        return;
    }
    build(ls,pl,mid);
    build(rs,mid+1,pr);
    push_up(p);
}

void update(int p,int pl,int pr,int k,int d) {
    if(pl == pr) {
        t[p].r[1] = d;
        t[p].len = 1;
        return;
    }
    if(k <= mid) update(ls,pl,mid,k,d);
    else update(rs,mid+1,pr,k,d);
    push_up(p); 
}

node query(int p,int pl,int pr,int l,int r) {
    if(l <= pl && pr <= r) return t[p];
    if(r <= mid) return query(ls,pl,mid,l,r);
    else if(l > mid) return query(rs,mid+1,pr,l,r);
    else {
        node T = query(ls,pl,mid,l,r),Q = query(rs,mid + 1,pr,l,r);
        node c = merge(T,Q);
        return c;
    } 
}
#undef ls
#undef rs
#undef mid
}

int n,q;

void getans(sgt::node P) {
    int i = 1,j = 2,k = 3;
    if(P.len < 3) goto End;
    for(;k<=P.len;i++,j++,k++) {
        if(P.r[i] < P.r[j] + P.r[k]) {
            wt(P.r[i] + P.r[j] + P.r[k]);
            putchar('\n');
            return;
        }
    }
    End:
    putchar('0'),putchar('\n');
}

signed main() {
	freopen("triangle.in","r",stdin);
	freopen("triangle.out","w",stdout);
	n = rd(),q = rd();
    for(int i = 1;i<=n;i++) A[i] = rd();
    sgt::build(1,1,n);
    while(q--) {
        int opt = rd();
        if(opt) {
            int l = rd(),r = rd();
            getans(sgt::query(1,1,n,l,r));
        }else {
            int p = rd(),v = rd();
            sgt::update(1,1,n,p,v);
        }
    }
	return 0;
}
A. 随机(random)

题面：

题目描述

给一个随机的 1-n 的排列，求这个排列所有子区间，一共有 \frac{n\times (n+1)}{2} 个，他们每一个的中位数之和。

中位数的定义是所以数从小到大排序之后的第 floor(\frac{(n+1)}{2}) 个

这题只要出 90 90 90 分 ( n ≤ 2500 ) (n \leq 2500) (n≤2500) 就可以了

那么，我的思路是(离散化后线段树上询问前 k k k 大值 + 双指针区间询问)

不多说，上 A C AC AC 代码

AC-code:

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 3e4+5;

int n,a[N],b[N],c[N];

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)

int t[N<<2];

void push_up(int p) {
    t[p] = t[ls] + t[rs];
}

void update(int p,int pl,int pr,int k,int d) {
    if(pl == pr) {
        t[p] += d;
        return;
    }
    if(k <= mid) update(ls,pl,mid,k,d);
    else update(rs,mid+1,pr,k,d);
    push_up(p);
} 

int kth(int p,int pl,int pr,int k) {
    if(pl == pr) return pl;
    if(t[ls] >= k) return kth(ls,pl,mid,k);
    return kth(rs,mid+1,pr,k - t[ls]);
}

#undef ls
#undef rs
#undef mid
}



signed main() {
    freopen("random.in","r",stdin);
    freopen("random.out","w",stdout);

    n = rd();
    for(int i = 1;i<=n;i++) a[i] = rd();
    for(int i = 1;i<=n;i++) c[i] = b[i] = a[i];
    sort(b + 1,b + n + 1);
    int top = unique(b + 1,b + n + 1) - b - 1;
    for(int i = 1;i<=n;i++) c[i] = lower_bound(b + 1,b + top + 1,c[i]) - b;
    int ans = 0;
    for(int i = 1;i<=n;i++) ans += a[i];
    int l = 1,r = 0;
    for(int i = 1;i<n;i += 2) {
        for(int j = i + 1;j<=n;j++) {
            while(l > i) sgt::update(1,1,n,c[--l],1);
            while(r < j) sgt::update(1,1,n,c[++r],1);
            while(l < i) sgt::update(1,1,n,c[l++],-1);
            while(r > j) sgt::update(1,1,n,c[r--],-1);
            int len = j - i + 1;
            if(len & 1) ans += b[sgt::kth(1,1,n,(len + 1) / 2)];
			else ans += b[sgt::kth(1,1,n,len/2)];
        }
        int k = i + 1;
        if(k >= n) break;
        for(int j = n;j>k;j--) {
            while(l > k) sgt::update(1,1,n,c[--l],1);
            while(r < j) sgt::update(1,1,n,c[++r],1);
            while(l < k) sgt::update(1,1,n,c[l++],-1);
            while(r > j) sgt::update(1,1,n,c[r--],-1);
            int len = j - k + 1;
            if(len & 1) ans += b[sgt::kth(1,1,n,(len + 1) / 2)];
			else ans += b[sgt::kth(1,1,n,len/2)];
        }
    }

    wt(ans);
	

	return 0;
}

2024/07/21

放假，好耶！

来点整数分块提提神

P2261 [CQOI2007] 余数求和

题面：

题目描述

给出正整数 n n n 和 k k k，请计算

G ( n , k ) = ∑ i = 1 n k   m o d   i G(n, k) = \sum_{i = 1}^n k \bmod i G(n,k)=i=1∑n​kmodi

其中 k   m o d   i k\bmod i kmodi 表示 k k k 除以 i i i 的余数。

输入格式

输入只有一行两个整数，分别表示 n n n 和 k k k。

输出格式

输出一行一个整数表示答案。

样例 #1
样例输入 #1
10 5
样例输出 #1
29
提示
样例 1 解释

G ( 10 , 5 ) = 0 + 1 + 2 + 1 + 0 + 5 + 5 + 5 + 5 + 5 = 29 G(10, 5)=0+1+2+1+0+5+5+5+5+5=29 G(10,5)=0+1+2+1+0+5+5+5+5+5=29。

数据规模与约定
  • 对于 30 % 30\% 30% 的数据，保证 n , k ≤ 1 0 3 n , k \leq 10^3 n,k≤103。
  • 对于 60 % 60\% 60% 的数据，保证 n , k ≤ 1 0 6 n, k \leq 10^6 n,k≤106。
  • 对于 100 % 100\% 100% 的数据，保证 1 ≤ n , k ≤ 1 0 9 1 \leq n, k \leq 10^9 1≤n,k≤109。

2024/2/13 添加一组 hack 数据

我们要求什么？拆式子！
G ( n , k ) = ∑ i = 1 n ( k   %   i ) = ∑ i = 1 n ( k − i ⋅ ⌊ k i ⌋ ) G ( n , k ) = n k − ∑ i = 1 n ( i ⋅ ⌊ k i ⌋ ) G(n,k) = \sum_{i = 1}^n (k\ \%\ i) = \sum_{i = 1}^n(k - i \cdot \lfloor \frac{k}{i} \rfloor) \\ G(n,k) = nk - \sum_{i = 1}^n (i \cdot \lfloor \frac{k}{i} \rfloor) G(n,k)=i=1∑n​(k % i)=i=1∑n​(k−i⋅⌊ik​⌋)G(n,k)=nk−i=1∑n​(i⋅⌊ik​⌋)
n k nk nk 部分可以 O ( 1 ) O(1) O(1) 算，废话
现在我们要求什么？分解问题！

[ 1 ∼ n ] [1 \sim n] [1∼n] 太广了，那么我们进行整数分块！
当一个块左端点为 l l l，那么右端点就可以求出，为 ⌊ k ⌊ k l ⌋ ⌋ \lfloor \frac{k}{\lfloor \frac{k}{l} \rfloor}\rfloor ⌊⌊lk​⌋k​⌋

那么对于一个左端点为 l l l 的块，对于答案 a n s ans ans

a n s ← ( a n s − ( k / l ) ∑ i = l r i ⇔ a n s − ( k / l ) ⋅ ( r − l + 1 ) ⋅ ( l + r ) / 2 ) ans \leftarrow (ans - (k / l) \sum_{i = l}^r i \Leftrightarrow ans - (k / l) \cdot (r - l + 1) \cdot (l + r) / 2) ans←(ans−(k/l)i=l∑r​i⇔ans−(k/l)⋅(r−l+1)⋅(l+r)/2)

时间复杂度 O ( n ) O(\sqrt{n}) O(n ​)
此题结束！
AC-code：

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

int n,k;

signed main() {
	int l,r,res = 0;
	n = rd(),k = rd();
	res += n * k;
	for(int l = 1;l<=n;l = r + 1){
		if(k / l == 0) break;
		r = min(n,k / (k / l));
		res -= (k / l) * (r - l + 1)*(r + l) / 2;
	}
	wt(res);

	return 0;
}

P4001 [ICPC-Beijing 2006] 狼抓兔子

题面：

题目描述

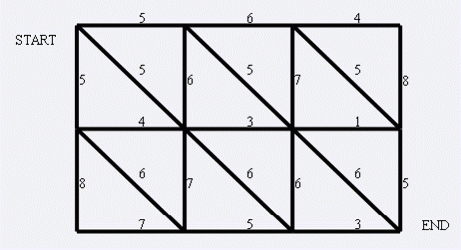
现在小朋友们最喜欢的"喜羊羊与灰太狼"。话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

左上角点为 ( 1 , 1 ) (1,1) (1,1)，右下角点为 ( N , M ) (N,M) (N,M)（上图中 N = 3 N=3 N=3， M = 4 M=4 M=4）。有以下三种类型的道路：

  1. ( x , y ) ⇌ ( x + 1 , y ) (x,y)\rightleftharpoons(x+1,y) (x,y)⇌(x+1,y)

  2. ( x , y ) ⇌ ( x , y + 1 ) (x,y)\rightleftharpoons(x,y+1) (x,y)⇌(x,y+1)

  3. ( x , y ) ⇌ ( x + 1 , y + 1 ) (x,y)\rightleftharpoons(x+1,y+1) (x,y)⇌(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的。左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角 ( 1 , 1 ) (1,1) (1,1) 的窝里，现在它们要跑到右下角 ( N , M ) (N,M) (N,M) 的窝中去，狼王开始伏击这些兔子。当然为了保险起见，如果一条道路上最多通过的兔子数为 K K K，狼王需要安排同样数量的 K K K 只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

输入格式

第一行两个整数 N , M N,M N,M，表示网格的大小。

接下来分三部分。

第一部分共 N N N 行，每行 M − 1 M-1 M−1 个数，表示横向道路的权值。

第二部分共 N − 1 N-1 N−1 行，每行 M M M 个数，表示纵向道路的权值。

第三部分共 N − 1 N-1 N−1 行，每行 M − 1 M-1 M−1 个数，表示斜向道路的权值。

输出格式

输出一个整数，表示参与伏击的狼的最小数量。

样例 #1
样例输入 #1
3 4
5 6 4
4 3 1
7 5 3
5 6 7 8
8 7 6 5
5 5 5
6 6 6
样例输出 #1
14
提示
数据规模与约定

对于全部的测试点，保证 3 ≤ N , M ≤ 1000 3 \leq N,M \leq 1000 3≤N,M≤1000，所有道路的权值均为不超过 1 0 6 10^6 106 的正整数。

关键在 网格图转对偶图

然后建图跑最短路

最恶心的是建图

AC-code：

#include<bits/stdc++.h>
using namespace std;

#define int long long

int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

constexpr int N = 1005,M = 6e6+5;
int n,m;

int head[2100000],nxt[M],to[M],cnt,val[M];

void init() {memset(head,-1,sizeof(head));}

void add(int u,int v,int w) {
	nxt[cnt] = head[u];
	to[cnt] = v;
	val[cnt] = w;
	head[u] = cnt++;
}

int a[N][N],b[N][N],c[N][N];
int S,E,dis[2100000];
bool vis[2100000];

struct node{
	int x,w;
	node(int x,int w) :x(x),w(w){}
	bool operator < (const node &a) const{
		return a.w < w;
	}
};

void dij(){
	memset(dis,0x3f,sizeof(dis));
	priority_queue<node> q;
	q.push(node(S,0));
	dis[S] = 0;
	while(q.size()){
		node t = q.top();
		q.pop();
		if(vis[t.x]) continue;
		vis[t.x] = true;
		for(int i = head[t.x];~i;i = nxt[i]) {
			int y = to[i],W = val[i];
			if(dis[y] > dis[t.x] + W) {
				dis[y] = dis[t.x] + W;
				if(!vis[y]) q.push(node(y,dis[y]));
			}
		}
	}
	
}

signed main() {
	init();
	n = rd(),m = rd();
	S = 0;E = (m - 1) * (n - 1) * 2 + 2;
	int ans = 0;
	for(int i = 1;i<=n;i++) 
		for(int j = 1;j<m;j++) 
			a[i][j] = rd();
	for(int i = 1;i<n;i++)
		for(int j = 1;j<=m;j++) 
			b[i][j] = rd();
	for(int i = 1;i<n;i++)
		for(int j = 1;j<m;j++)
			c[i][j] = rd();
	for(int i = 1;i<m;i++){
		add(2 * i,E,a[1][i]),add(E,2 * i,a[1][i]);
	}
	int k = (m - 1) * 2 * (n - 2);
	for(int i = 1;i<m;i++) {
		add(S,k + (2 * i) - 1,a[n][i]),add(k + (2 * i) - 1,S,a[n][i]);	
	}
	for(int i = 1;i<n;i++){
		k = (m - 1) * 2 * (i - 1) + 1;
		add(S,k,b[i][1]);add(k,S,b[i][1]);
	}
	for(int i = 2;i<=n;i++) {
		k = (m - 1) * 2 * (i - 1);
		add(k,E,b[i - 1][m]);add(E,k,b[i - 1][m]);
	}
	int layer = (m - 1) * 2;
	for(int i = 2;i<n;i++)
		for(int j = 1;j<m;j++) {
			int s = (i - 2) * layer + (j - 1) * 2 + 1;
			int e = (i - 1) * layer + j * 2;
			add(s,e,a[i][j]);add(e,s,a[i][j]);
		}

	for(int i = 1;i<n;i++) {
		for(int j = 2;j<m;j++) {
			int s = (i - 1) * layer + (j - 1) * 2;
			int e = s + 1;
			add(s,e,b[i][j]);add(e,s,b[i][j]);
		}
	}
	
	for(int i = 1;i<n;i++)	
		for(int j = 1;j<m;j++) {
			int s = (i - 1) * layer + (j - 1) * 2 + 1;
			int e = s + 1;
			add(s,e,c[i][j]);add(e,s,c[i][j]);
		}
	dij();

	wt(dis[E]);

	return 0;
}
MingJunYi
关注
  • 8
    点赞
  • 踩
  • 9
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
go1.22.3.linux-amd64.tar.gz
05-22
go1.22.3.linux-amd64.tar.gz是Go语言截止2024年5月22日的最新版，欢迎下载使用。go1.22.3.linux-amd64.tar.gz是Go语言截止2024年5月22日的最新版，欢迎下载使用。go1.22.3.linux-amd64.tar.gz是Go语言截止2024年5月...
Kali Linux VMware（kali-linux-2022.2-vmware-amd64.part1.rar)
06-14
Kali Linux VMware（kali-linux-2022.2-vmware-amd64.7z）文件分割成 3个 压缩包，必须集齐3个 文件后才能一起解压一起使用： kali-linux-2022.2-vmware-amd64.part1.rar ... kali-linux-2022.2-vmware-amd64.part2.rar...
2024.8 - 做题记录与方法总结 - Part 3
MingJunYi的博客
08-21 407
C. 野火 题目描述 B 国有 n 座城市，有 m 条双向道路连接着这些城市。城市编号为 1 到 n，道路编号为 1 到 m。经由这些道路，从 B 国中任意一个城市出发，均能到达其他所有城市。特别地，这里保证 m\le n。 由于能源不足，B 国的第 i 条道路只能正常运行 d_i 个时刻。现在 Yoimiya 需要给每一条道路选择一个开始运行的时间 s_i，那么这条道路就会在 [s_i,s_i+d_i-1] 这些时刻内正常运行。保证 d_i\ge 1。 B 国的大守护
2024.8 - 做题记录与方法总结 - Part 2
MingJunYi的博客
08-21 343
首先不难发现的是，只要字母出现次数对的上，我们必然有一种方法重排（就是假设全部重来，把所有字母都按顺序放到一个空字符串中）我们发现，我们每拿一个字符，就有一坨字符从前面掉到后面，那么我们就可以通过这个过程来省事。在种完这些花之后，小 N 想要在她的花园中选出一个子矩形，使得这片子矩形中恰好种有。的从后往前的子序列 进行最大匹配，就可以求出不用动的字符数。现在小 N 要在花园的某些位置种上花，具体来说，可以用。这个奇怪的描述矩形的方式，一看就很奇怪，非常值得关注。具体来说，设她选出的矩形的左上角是。
2024.8 - 做题记录与方法总结 - Part 4
最新发布
MingJunYi的博客
08-21 295
flame注意到，猫猫通过的路径上的小写字母可以组成一个字符串，他想考考mybing：在猫猫所有的移动方案中，构成的字典序最小的字符串是什么呢？我们子树内的军营建造完了，同时子树内的军营方案和道路看守方案也都完备了，最开始的时候，他们把他们的游戏角色——猫猫棋子，放在左上角坐标。的数据，保证每一个位置下边和右边的位置中字母都不同。这明显不对，因为答案肯定是随子树的增大而递增的。子树内的边数，用总边数减去，就是外面的边数。我们发现我们没有要处理的子树外的边，（因为。缩点 + tarjan + 树形dp。
2024.7 - 做题记录与方法总结-Part2
MingJunYi的博客
08-21 240
2024/07/09 校内模拟赛 #1 Codeforces Round 936 (Div. 2) -> E. Girl Permutation 题面： 某个长度为 nnn 的排列需要被猜中。 您将得到其前缀最大值和后缀最大值的索引。 长度为 kkk 的排列是一个大小为 kkk 的数组，从 111 到 kkk 的每个整数都正好出现一次。 前缀最大值是指在以该元素结尾的前缀上最大的元素。更正式地说，如果每个 jjj < iii 的 aia_iai​ > aja_jaj​ 都是前缀最大值，那
2024.7 - 做题记录与方法总结 - Part 4
MingJunYi的博客
08-21 511
2024/07/23 梦熊题单 E.基础数据结构题 题目描述 给定一个长度为 n 的序列 A ，下标从 1 开始，你需要维护三种操作： 1{\kern 4pt}l{\kern 4pt}r{\kern 4pt}x: 对于 l \leq i \leq r ，令 A_i=A_i+x 。 2{\kern 4pt}l{\kern 4pt}r: 对于 l \leq i \leq r ，令 A_i=\lfloor \sqrt{A_i} \rfloor 。 3{\kern 4pt}l{
2024.7 - 做题记录与方法总结-Part1
MingJunYi的博客
08-21 512
2024/07/01 AtCoder Beginner Contest 360 E - Random Swaps of Balls 期望 dpdpdp 题 问题陈述 有 N−1N - 1N−1 个白球和一个黑球。这些 NNN 个球排成一排，黑球最初位于最左边的位置。 高桥正好要进行下面的操作 KKK 次。 在 111 和 NNN 之间均匀随机地选择一个整数，包括两次。设 aaa 和 bbb 为所选整数。如果是 a≠ba \neq ba=b ，把左边的 aaa -th 和 bbb -th 两个球交换。
2024.8 - 做题记录与方法总结 - Part 1
MingJunYi的博客
08-21 213
2024.8 - Record of Questions and Summary of Methodology 先分享一个歌单： 永无止境的八月！ 2024/08/01 先来点重量级的 P4768 [NOI2018] 归程 题面： [NOI2018] 归程 题目描述 本题的故事发生在魔力之都，在这里我们将为你介绍一些必要的设定。 魔力之都可以抽象成一个 nnn 个节点、mmm 条边的无向连通图（节点的编号从 111 至 nnn）。我们依次用 l,al,al,a 描述一条边的长度、海拔。 作为季风气候的代
创新实训周报2024.6.16
u010649319的博客
06-24 617
实体链接的目标是识别文本中的实体提及（mention）并将其链接到知识库中的相应实体。双编码器分别编码文本和实体，生成嵌入向量，然后通过向量检索来找到与文本嵌入向量最接近的实体嵌入向量，从而生成候选实体。在第二阶段，BLINK 使用交互式编码器模型对第一阶段生成的候选实体进行排序，选择最可能的实体。：使用内积或余弦相似度计算mention嵌入向量与实体嵌入向量之间的相似度，检索出前k个最相似的实体作为候选实体。：根据相似度得分对候选实体进行排序，选择得分最高的实体作为最终链接的实体。
SCAU期末笔记 - 程序设计与算法基础（内含隐藏题库）
swan416的博客
05-20 725
SCAU的程序设计与算法基础课在校内oj的习题总结 个人整理
Android Studio Koala（android-studio-2024.1.1.11-windows.zip.002）
07-04
Android Studio Koala 2024.1.1（android-studio-2024.1.1.11-windows.zip）适用于Windows系统，文件使用360压缩软件分割成两个压缩包，必须一起下载使用： part1: ...
kali-linux-2023.3-vmware-amd64.part1.rar
10-13
kali-linux-2023.3（kali-linux-2023.3-vmware-amd64.7z）适用于VMware系统，文件使用WinRAR分割成四个压缩包，必须一起下载使用: 文件1：https://download.csdn.net/download/weixin_43800734/88423344 文件2：...
Android Studio Jellyfish（android-studio-2023.3.1.18-windows.p1）
05-14
Android Studio Jellyfish 2023.3.1（android-studio-2023.3.1.18-windows.exe）适用于Windows系统，文件使用360压缩软件分割成两个压缩包，必须一起下载使用： part1: ...
【Python】生成二维迷宫的算法
HarryXYC的博客
08-16 323
基于Pygame和PIL的迷宫生成器
代码随想录算法训练营第十七天（二叉树 五）
b1ankwall的博客
08-16 768
参加代码随想录第43期算法训练营day17|654.最大二叉树，617.合并二叉树，700.二叉搜索树中的搜索，98.验证二叉搜索树
【算法】马踏棋盘（骑士周游）问题回溯算法实现以及使用贪心算法优化
2302_78914800的博客
08-18 504
将马儿随机放在国际象棋的 8*8 棋盘的某个方格中，马儿按照“马走日”进行移动，要求每个方格只进入一次，走遍棋盘上全部 64 个方格。注意：马儿不同的走法会得到不同的结果，效率也会有影响。
Leetcode 219. 存在重复元素 II
铁马冰河入梦来
08-20 210
哈希表解决存在重复元素二问题
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值