P2495 [SDOI2011] 消耗战
题面:
题目描述
在一场战争中,战场由 n n n 个岛屿和 n − 1 n-1 n−1 个桥梁组成,保证每两个岛屿间有且仅有一条路径可达。现在,我军已经侦查到敌军的总部在编号为 1 1 1 的岛屿,而且他们已经没有足够多的能源维系战斗,我军胜利在望。已知在其他 k k k 个岛屿上有丰富能源,为了防止敌军获取能源,我军的任务是炸毁一些桥梁,使得敌军不能到达任何能源丰富的岛屿。由于不同桥梁的材质和结构不同,所以炸毁不同的桥梁有不同的代价,我军希望在满足目标的同时使得总代价最小。
侦查部门还发现,敌军有一台神秘机器。即使我军切断所有能源之后,他们也可以用那台机器。机器产生的效果不仅仅会修复所有我军炸毁的桥梁,而且会重新随机资源分布(但可以保证的是,资源不会分布到 1 1 1 号岛屿上)。不过侦查部门还发现了这台机器只能够使用 m m m 次,所以我们只需要把每次任务完成即可。
输入格式
第一行一个整数 n n n,表示岛屿数量。
接下来 n − 1 n-1 n−1 行,每行三个整数 u , v , w u,v,w u,v,w ,表示 u u u 号岛屿和 v v v 号岛屿由一条代价为 w w w 的桥梁直接相连。
第 n + 1 n+1 n+1 行,一个整数 m m m ,代表敌方机器能使用的次数。
接下来 m m m 行,第 i i i 行一个整数 k i k_i ki ,代表第 i i i 次后,有 k i k_i ki 个岛屿资源丰富。接下来 k i k_i ki 个整数 h 1 , h 2 , . . . , h k i h_1,h_2,..., h_{k_i} h1,h2,...,hki ,表示资源丰富岛屿的编号。
输出格式
输出共 m m m 行,表示每次任务的最小代价。
样例 #1
样例输入 #1
10 1 5 13 1 9 6 2 1 19 2 4 8 2 3 91 5 6 8 7 5 4 7 8 31 10 7 9 3 2 10 6 4 5 7 8 3 3 9 4 6样例输出 #1
12 32 22提示
数据规模与约定
- 对于 10 % 10\% 10% 的数据, n ≤ 10 , m ≤ 5 n\leq 10, m\leq 5 n≤10,m≤5 。
- 对于 20 % 20\% 20% 的数据, n ≤ 100 , m ≤ 100 , 1 ≤ k i ≤ 10 n\leq 100, m\leq 100, 1\leq k_i\leq 10 n≤100,m≤100,1≤ki≤10 。
- 对于 40 % 40\% 40% 的数据, n ≤ 1000 , 1 ≤ k i ≤ 15 n\leq 1000, 1\leq k_i\leq 15 n≤1000,1≤ki≤15 。
- 对于 100 % 100\% 100% 的数据, 2 ≤ n ≤ 2.5 × 1 0 5 , 1 ≤ m ≤ 5 × 1 0 5 , ∑ k i ≤ 5 × 1 0 5 , 1 ≤ k i < n , h i ≠ 1 , 1 ≤ u , v ≤ n , 1 ≤ w ≤ 1 0 5 2\leq n \leq 2.5\times 10^5, 1\leq m\leq 5\times 10^5, \sum k_i \leq 5\times 10^5, 1\leq k_i< n, h_i\neq 1, 1\leq u,v\leq n, 1\leq w\leq 10^5 2≤n≤2.5×105,1≤m≤5×105,∑ki≤5×105,1≤ki<n,hi=1,1≤u,v≤n,1≤w≤105。
虚树由此而来
为什么有了虚树?
对于所有操作,均摊下来时并不大时,虚树就派上了用场
我们在本题发现 Σ k \Sigma k Σk 与 m m m 是等阶的数据范围
如果按照朴素的解法,我们对于每一次操作,都去跑一遍树上dp
复杂度直接爆炸!
需要发现的是,每一次需要dp的点均摊下来其实很有限
我们只针对这些需要dp的点dp就可以了,
不去多管闲事。
虚树登场
建虚树的方法来自这个博客,讲的非常好
如何建立虚树
最右链是虚树构建的一条分界线,表明其左侧部分的虚树已经完成构建。我们使用栈 s t a k stak stak来维护所谓的最右链, t o p top top为栈顶位置。值得注意的是,最右链上的边并没有被加入虚树,这是因为在接下来的过程中随时会有某个 l c a lca lca插到最右链中。
初始无条件将第一个询问点加入栈 s t a k stak stak中。
将接下来的所有询问点顺次加入,假设该询问点为 n o w now now, l c lc lc为该点和栈顶点的最近公共祖先即 l c = l c a ( s t a k [ t o p ] , n o w ) lc=lca(stak[top],now) lc=lca(stak[top],now)。
由于 l c lc lc是 s t a k [ t o p ] stak[top] stak[top]的祖先, l c lc lc必然在我们维护的最右链上。
考虑 l c lc lc和 s t a k [ t o p ] stak[top] stak[top]及栈中第二个元素 s t a k [ t o p − 1 ] stak[top-1] stak[top−1]的关系。
情况一
l c = s t a k [ t o p ] lc=stak[top] lc=stak[top],也就是说, n o w now now在 s t a k [ t o p ] stak[top] stak[top]的子树中
这时候,我们只需把 n o w now now入栈,即把它加到最右链的末端即可。
情况二
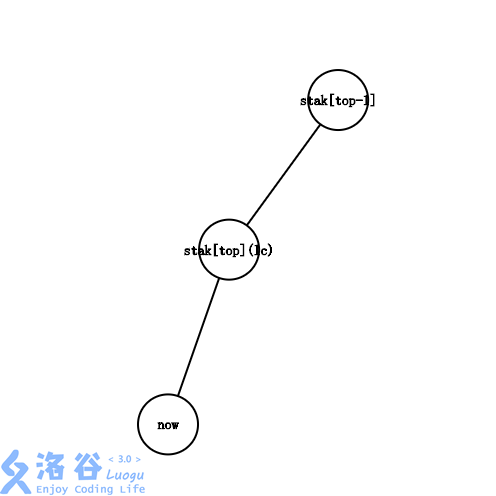
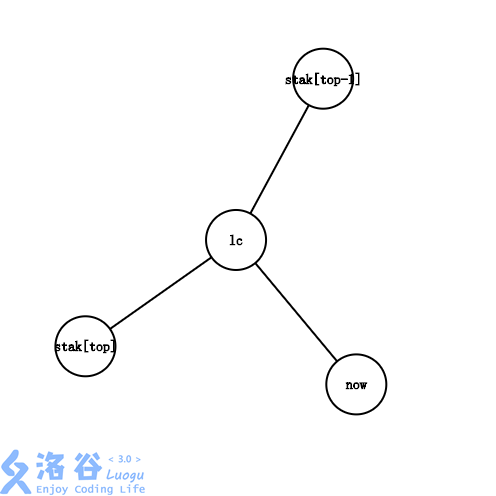
l c lc lc在 s t a k [ t o p ] stak[top] stak[top]和 s t a k [ t o p − 1 ] stak[top-1] stak[top−1]之间。
显然,此时最右链的末端从 s t a k [ t o p − 1 ] − > s t a k [ t o p ] stak[top-1]->stak[top] stak[top−1]−>stak[top]变成了 s t a k [ t o p − 1 ] − > l c − > s t a k [ t o p ] stak[top-1]->lc->stak[top] stak[top−1]−>lc−>stak[top],我们需要做的,首先是把边 l c − s t a k [ t o p ] lc-stak[top] lc−stak[top]加入虚树,然后,把 s t a k [ t o p ] stak[top] stak[top]出栈,把 l c lc lc和 n o w now now入栈。
情况三
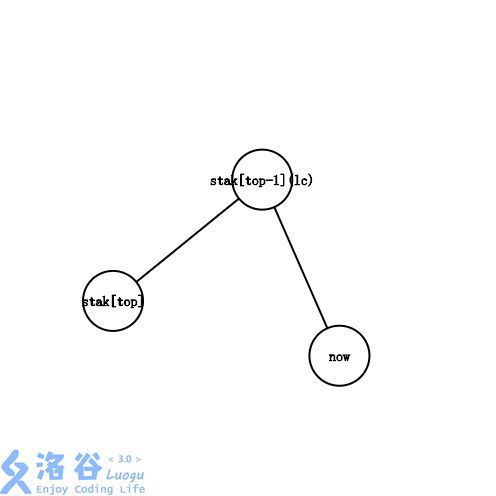
l c = s t a k [ t o p − 1 ] lc=stak[top-1] lc=stak[top−1]。
这种情况和第二种情况大同小异,唯一的区别就是 l c lc lc不用入栈了。
情况四
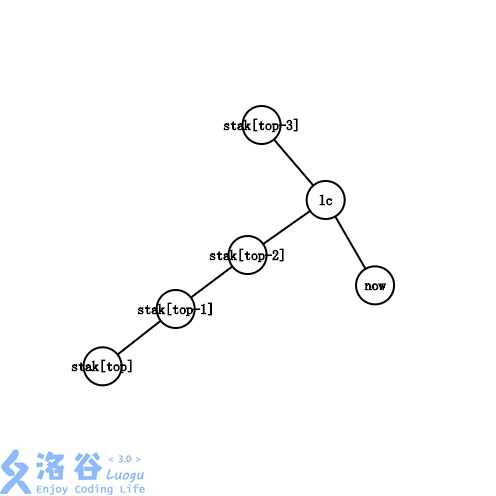
此时有 d e p [ l c ] < d e p [ s t a k [ t o p − 1 ] ] dep[lc]<dep[stak[top-1]] dep[lc]<dep[stak[top−1]]。 l c lc lc已经不在 s t a k [ t o p − 1 ] stak[top-1] stak[top−1]的子树中了,甚至也未必在 s t a k [ t o p − 2 ] , s t a k [ t o p − 3 ] . . . . . . stak[top-2],stak[top-3]...... stak[top−2],stak[top−3]......的子树中。
以图中为例,最右链从 s t a k [ t o p − 3 ] − > s t a k [ t o p − 2 ] − > s t a k [ t o p − 1 ] − > s t a k [ t o p ] stak[top-3]->stak[top-2]->stak[top-1]->stak[top] stak[top−3]−>stak[top−2]−>stak[top−1]−>stak[top]变成了 s t a k [ t o p − 3 ] − > l c − > n o w stak[top-3]->lc->now stak[top−3]−>lc−>now。我们需要循环依次将最右链的末端剪下,将被剪下的边加入虚树,直到不再是情况四。
就上图而言,循环会持续两轮,将 s t a k [ t o p ] , s t a k [ t o p − 1 ] stak[top],stak[top-1] stak[top],stak[top−1]依次出栈,并且把边 s t a k [ t o p − 1 ] − s t a k [ t o p ] , s t a k [ t o p − 2 ] − s t a k [ t o p − 1 ] stak[top-1]-stak[top],stak[top-2]-stak[top-1] stak[top−1]−stak[top],stak[top−2]−stak[top−1]加入虚树中。随后通过>情况二完成构建。
当最后一个询问点加入之后,再将最右链加入虚树,即可完成构建。
一些问题
- 如果栈 s t a k stak stak中仅仅有一个元素,此时 s t a k [ t o p − 1 ] stak[top-1] stak[top−1]是否会出问题?
对于栈 s t a k stak stak,我们从 1 1 1开始储存。那么在这种情况下, s t a k [ t o p − 1 ] = 0 stak[top-1]=0 stak[top−1]=0,并且 d e p [ 0 ] = 0 dep[0]=0 dep[0]=0。此时 d e p [ l c ] < d e p [ s t a k [ t o p − 1 ] ] dep[lc]<dep[stak[top-1]] dep[lc]<dep[stak[top−1]]恒成立。也就是说,> s t a k [ 0 ] stak[0] stak[0]扮演了深度最小的哨兵,确保了程序只会进入情况一和二。
- 如何在一次询问结束后清空虚树?
不能直接对图进行清空,否则复杂度会退化到 O ( n ) O(n) O(n)的复杂度,这是我们无法承受的。在 d f s dfs dfs的过程中每当访问完一个结点就进行清空即可。
如若侵权,请在该评论区联系我,即删
该部分的代码(简单分讨):
bool cmp(int x,int y) {return id[x] < id[y];}
---------------------------------------------
sort(a.begin(),a.end(),cmp);
st[tp = 1] = a[0];
for(int i = 1;i<k;i++) {
int now = a[i];
int LCA = lca(now,st[tp]);
while(1)
if(dep[LCA] >= dep[st[tp - 1]]) {
if(LCA != st[tp]) {
G.add(LCA,st[tp],0);
if(LCA != st[tp - 1])
st[tp] = LCA;
else
tp--;
}
break;
}else {
G.add(st[tp - 1],st[tp],0);
tp--;
}
st[++tp] = now;
}
本题中,我们要求 1 1 1 节点(根节点)与关键点互不连通的最小代价
我们用 m i n v minv minv 数组存储每个点与根节点不连通的最小代价
这部分的代码(我个人喜欢树剖求LCA,这个部分和树剖放在了一起):
void dfs1(int x,int f) {
fa[x] = f;
siz[x] = 1;
dep[x] = dep[f] + 1;
for(int i = g.head[x];~i;i = g.nxt[i]) {
int y = g.to[i];
if(y ^ f) {
minv[y] = min(minv[x],g.val[i]); <------
dfs1(y,x);
siz[x] += siz[y];
if(siz[son[x]] < siz[y]) son[x] = y;
}
}
}
对于答案,我们在虚树上统计
如果该点不是关键点,那么我们需要知道ta与子树内关键点不连通的最小代价、和ta本身与根节点不连通的代价,即:
c
o
s
t
x
=
min
{
∑
y
∈
s
o
n
x
c
o
s
t
y
,
m
i
n
v
x
}
cost_x = \min\{\sum_{y \in son_x}cost_y,minv_x\}
costx=min{y∈sonx∑costy,minvx}
如果该点是关键点,那么我们必须切断该点到根节点的一条边,这条边可能是
x
→
f
a
x \rightarrow fa
x→fa 的 边、或是
f
a
⇝
r
o
o
t
fa \leadsto root
fa⇝root 中的边(这个边我们在上面的式子中已经求过了)
所以:
c
o
s
t
x
=
m
i
n
v
x
cost_x = minv_x
costx=minvx
答案为: c o s t r o o t cost_{root} costroot
AC-code:
#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
int x = 0, w = 1;
char ch = 0;
while (ch < '0' || ch > '9') {
if (ch == '-') w = -1;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = x * 10 + (ch - '0');
ch = getchar();
}
return x * w;
}
void wt(int x) {
static int sta[35];
int f = 1;
if(x < 0) f = -1,x *= f;
int top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
if(f == -1) putchar('-');
while (top) putchar(sta[--top] + 48);
}
const int N = 5e5 + 5,inf = 0x3f3f3f3f3f3f3f3fLL;
struct edge{
int head[N],nxt[N<<1],to[N<<1],val[N<<1],cnt;
edge() {memset(head,-1,sizeof(head));cnt = 0;}
void init() {memset(head,-1,sizeof(head));cnt = 0;}
void add(int u,int v,int w) {
nxt[cnt] = head[u];
to[cnt] = v;
val[cnt] = w;
head[u] = cnt++;
}
};
edge g,G;
int n,q,k;
int fa[N],siz[N],top[N],dep[N],id[N],son[N],num,minv[N];
void dfs1(int x,int f) {
fa[x] = f;
siz[x] = 1;
dep[x] = dep[f] + 1;
for(int i = g.head[x];~i;i = g.nxt[i]) {
int y = g.to[i];
if(y ^ f) {
minv[y] = min(minv[x],g.val[i]);
dfs1(y,x);
siz[x] += siz[y];
if(siz[son[x]] < siz[y]) son[x] = y;
}
}
}
void dfs2(int x,int topx) {
top[x] = topx;
id[x] = ++num;
if(!son[x]) return;
dfs2(son[x],topx);
for(int i = g.head[x];~i;i = g.nxt[i]) {
int y = g.to[i];
if(y ^ fa[x] && y ^ son[x]) dfs2(y,y);
}
}
int lca(int x,int y) {
while(top[x] ^ top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x,y);
x = fa[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
bool cmp(int x,int y) {return id[x] < id[y];}
int st[N],tp;
bool query[N];
int dfs(int x) {
int sum = 0;
int tmp = 0;
for(int i = G.head[x];~i;i = G.nxt[i]) {
int y = G.to[i];
sum += dfs(y);
}
if(query[x])
tmp = minv[x];
else
tmp = min(minv[x],sum);
query[x] = false;
G.head[x] = -1;
return tmp;
}
void solve() {
k = rd();
vector<int> a(k);
for(int i = 0;i<k;i++) a[i] = rd();
for(int i = 0;i<k;i++) query[a[i]] = 1;
sort(a.begin(),a.end(),cmp);
st[tp = 1] = a[0];
for(int i = 1;i<k;i++) {
int now = a[i];
int LCA = lca(now,st[tp]);
while(1)
if(dep[LCA] >= dep[st[tp - 1]]) {
if(LCA != st[tp]) {
G.add(LCA,st[tp],0);
if(LCA != st[tp - 1])
st[tp] = LCA;
else
tp--;
}
break;
}else {
G.add(st[tp - 1],st[tp],0);
tp--;
}
st[++tp] = now;
}
while(--tp)
G.add(st[tp],st[tp + 1],0);
wt(dfs(st[1]));
putchar('\n');
}
signed main() {
minv[1] = inf;
n = rd();
for(int i = 1,u,v,w;i<n;i++) {
u = rd(),v = rd(),w = rd();
g.add(u,v,w);g.add(v,u,w);
}
dfs1(1,0);dfs2(1,1);
q = rd();
while(q--) solve();
return 0;
}
题外话:
这是树剖和倍增求LCA的区别


哪个是倍增不用我多说吧?






















 167
167

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








