Sim-to-Real Learning of All Common Bipedal Gaitsvia Periodic Reward Composition论文解读-CSDN博客

本文链接：https://blog.csdn.net/qq_49925517/article/details/147901934

这是一篇几年前关于的Cassie腿部运动方法，论文虽然没有给源代码，但是文章内容非常详细

[2011.01387] Sim-to-Real Learning of All Common Bipedal Gaits via Periodic Reward Composition

INTRODUCTION

1. 研究目的

作者针对双足机器人底盘，也就是类似cassie这种，通过强化学习设计奖励函数，在不使用轨迹跟踪的条件下（因为稳定的轨迹难以获取，且泛化性差），用一个模型实现双足机器人所有常见的双足步态，包括：站立，行走，跳跃，奔跑等，且可以进行平滑的切换

2. 面临的问题

不同步态学习的关键问题在于如何构造奖励函数，使其既能明确表达预期的运动模式，又足够灵活以适应环境变化。

现有的常见方法是，给定精确的参考轨迹，这个方法确实解决了前面的第一个问题，即能明确表达预期的运动模式，参考轨迹只捕获了不同条件下实现步态特征的一小部分变化，这样对于步态的鲁棒性的影响是负面的
另一种不适用参考轨迹的方法，往往不够具体（比如只给一个前进的速度奖励），这样机器人学到的行为之间差异很大，需要不断的调试，细化奖励的设计，适应性差

3. Motivation

常见的双足步态，对于每只足，都可以分化为swing与stance两个阶段，而这两个阶段最显著的区别在于，足部对里面的力反馈与足部速度的互补存在与缺失。

即，Stance阶段，允许与地面的反馈力存在，而惩罚足部速度。Swing阶段，惩罚与地面的力反馈，而允许足部速度存在。

基于这样的框架，可以将常见双足步态描述为一系列的周期性运动阶段，在特定阶段惩罚或允许特定量。

这样用更加自然的奖励函数规范，充分约束RL学习的步态特征，并且适应性强。

4. 本文贡献

本文提出了一个设计奖励函数的原则性框架，可以捕获所有周期性双足运动的步态
在仿真中训练的策略可无缝迁移至真实机器人 Cassie，并实现多个步态间的切换

BACKGROUND

这里就简述一下背景，主要是当前双足运动的方法现状

双足步态的复杂性
自然界中的双足步态（如走、跑、跳等）具有明确的周期性结构，同时需要在不同环境下具备适应能力。如何让机器人学会这些步态，尤其是在现实世界中应用，尚未解决
奖励函数在步态学习中的核心作用
在强化学习中，奖励函数引导机器人行为的收敛方向。为学习特定步态，奖励函数需满足两个条件：
- 要足够明确，以促使策略学习到期望的步态模式；
- 同时也要不过于刚性，以保留适应不同动态与环境扰动的能力。
现有方法的局限性
- 许多方法依赖于预设的参考轨迹（如关节角度序列），这在一定程度上解决了“明确性”问题，但缺乏“适应性”，无法涵盖步态应对复杂环境的变异性。
- 而完全无参考的奖励函数通常设计得过于模糊或高度依赖经验调试，不具通用性，难以迁移与泛化

REWARD COMPOSITION

强化学习过程这里就不赘述了 skip

作者将机器人步态运动的奖励，分为了两个部分，一部分为周期运动有关的周期性（阶段性）奖励，另一个为全程存在，一般作为约束项（比如能量惩罚）或者控制项的奖励（比如速度方向命令）

整体框架如图

1. Preiodic Reward

1. 用 $\varphi$ 在[0,1]上循环，对时间进行索引，就是常见的正弦函数的变化，防止信号突变，现有的大部分足式机器人周期性运动都这样处理

2. 将周期性奖励范式为：

输入为当前观测值S与时钟信号 $\varphi$ ，beta为偏置，不用管。其中每个分量 $R_i(s,\phi)$ 用于捕获特定阶段步态的期望特征,表示为：

其中 $c_i$ 决定该项奖励对总奖励的影响（其实就是正奖励还是负奖励）。

$q_i(s)$ 是该项奖励的奖励度量值（譬如在站立阶段的力反馈奖励，这个就是采样的足部力反馈）。

$I_i(\phi)$ 是一个二维随机变量，输入为时钟信号，判断该时钟信号是否处于该项奖励的目标相位范围内，若在范围内，则为1。

其中 $I_i(\phi)$ 的分布用随机变量Ai和Bi来表示，分别代表阶段的开始与结束，它们由 Von Mises 分布建模，后者是环形分布（适合建模周期变量），近似于“包裹正态分布（wrapped normal）”。参数形式为 $(ai,bi,κ)$ ：分别是起始期望值、终止期望值，以及共享的集中程度（方差的倒数）。

也就是说，每一个阶段，对应一个A、B、k(这个不同阶段的值相同，为公共尺度)，输入一个时钟信号进去，函数会在A和B进行一个类似正态分布的采样，mean=A\B,std=k,然后生成多组区间，假设采样10次，也就是生成的10组区间，判断 $\varphi$ 是否在区间内。若 $\varphi$ 在（A+B）/2 附近，那么在区间内的概率肯定是1；但若 $\varphi$ 在A或者B附近，那么在区间内的概率是0到1之间线性变化的。这样避免了对阶段的刚性判断。

这个 $I_i(\phi)$ 还是蛮重要的，即使是现在，还有很多方法是刚性的周期判断处理，而作者这样处理后，对阶段边界的奖励有平滑作用，有“训练稳定性”与“可调节模糊性”的作用。

既然有了概率，那么奖励就变成了概率 * reward，也就是期望

2. Describing Bipedal Gaits

单脚的摆动与站立之间的循环作为奖励框架，奖励度量值选择足部力范数与足部速度范数 $q_{frc}(s)$ 与 $q_{spd}(s)$ 。摆动期间，允许足部速度，惩罚足部力，即 $c_{swing frc} = -1$ , $c_{swingspd} = 0$ 。类似的，站立阶段，惩罚足部速度，允许足部力量 $c_{swing frc} = 0$ ， $c_{swingspd} = -1$ 。

用比率 $r \in(0,1)$ 设置两阶段的时间间隔，使Swing阶段的持续长度为r,站立阶段的持续长度为1-r,并且两个阶段相互紧紧跟随，持续整个循环时间。

那么，每个足分站立与摆动两个阶段，每个阶段分速度与力反馈奖励，也就是2*2=4个奖励分量，如下：

下图用于理解相位变化与奖励的关系：

一个周期中，根据设计的步态，选择一个点为swing or stand的起点或者终点，根据比率r，决定了这个阶段的持续时间，阶段结束后，立刻进入下一个阶段，且持续时间为1-r。swing阶段，惩罚力反馈的值，所以 $E[ C_{frc}(\phi) ]$ 为-1，这样一旦采样到足部反馈力，就会有负的奖励；而站立阶段 $E[ C_{frc}(\phi) ]$ 为0，这样即使采样到足部反馈力，也不会有惩罚

这样一来，将速度与力的分量结合，重复两个阶段的预期总体return为:

另一方面，作者提到，双足步态中，双足其实都遵循相同的相位序列，只是相位时间上相互偏移，比如，在正常行走中，摆动和站立的持续时间分别为周期长度的一半，且相互偏移半个周期，而跳跃则是同时进入站立或摆动。

为了将单脚抬起和放置的简单行为扩展到双足步态的全部范围，只需要引入两个周期偏移参数 $\varphi$ 左， $\varphi$ 右，它们定义了左右脚相同行为阶段序列之间的精确时序位移。

最后，双足步态的预期总体奖励为：

3. 步态分析：

1. 跳跃

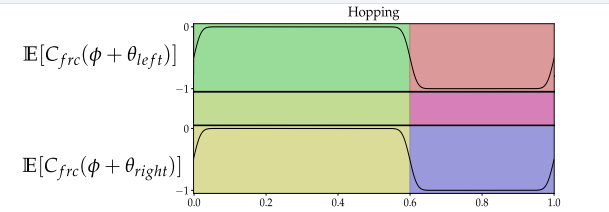
双足没有周期相位差，同时进入跳跃（摆动）阶段

2. 奔跑

双足有半个周期的相位差，且奔跑只有单脚站立和双脚摆动两个阶段，只需要比率r > 0.5即可，这里是0.6

3. 跳跑

这里就比较复杂，10 -> 01 -> 00 -> 01 -> 10 -> 00,两步跳跃？总之相位差也是半个周期，这里就可以显示作者方法的强大之处，只要是周期性循环的，都可以用这个框架来描述

METHOD

网络架构与action space

作者用的LSTM，两个循环隐藏层，节点数为128，动作空间为30（10个关节期望位置与10组PD参数），策略在40Hz下进行评估，机器人的PD控制器在2000Hz下运行

状态空间

作者提到，为了防止RL环境变成不稳定的MDP过程，需要将当前周期的编码，周期偏移参数（左和右），以及关于相位奖励组件的阶段的开始和结束时间的信息。

周期信号表示为：

L是整个循环中离散时间步长的个数。

为了将相位的开始和结束时间的信息编码到状态中，作者从相位时序中导出一个比率向量；每一个比率表示一个相在总周期中所占的比例。例如，开始时间为ai, j=0.3，结束时间为bi, j= 0.7的相位j应占总周期时间的40%(加上或减去一些不确定性) ；因此，我们可以推导出比值rj =0.4，且将比率提供给策略。

最后，策略的输入，也就是观测空间为：

第一行为机器人自身状态，也就是朝向，关节位置，根部速度，关节速度；第二行为控制命令，第三行为前面提到的比率r与时钟信号

奖励公式

前面的公式2作为足部运动描述的周期性奖励框架；为了实现运动的稳定性，且sim2real,需要加一些惩罚项；然后实现命令的跟踪，需要增加命令相关奖励项。这三个分支组成整体的奖励。

一个命令奖励，用于跟踪方向和行进速度；一个smooth奖励，就是防止扭矩、action、根部加速度变化突变过大。

Dynamics Randomization

这个没什么好说的，就是加随机，弥补sim与real的gap，现在的方法可以对运动学建模 +动力学随机，或者类似ASAP，用der_action来弥补。对于步态任务来说，运动学建模 +动力学随机就够了，或者动力学随机就行。

PPO算法

这个同样没什么好说的，现在大家都用的这个迭代算法，作者提到，他们为了保证运动的对称性，增加了一个mirror loss。

EXPERIMENTAL

Train Details

为了学习高效的步态策略，作者使用了 Proximal Policy Optimization（PPO）算法，并进行了如下配置：

轨迹批次（Batch）：每次训练以 32 条轨迹为单位，每条轨迹最长为 300 个时间步。
学习率（Learning Rate）：Actor 和 Critic 网络统一设为 0.0001。
重放缓冲区（Replay Buffer）：缓存 50,000 条状态转移数据。
训练轮数（Epochs）：每次迭代执行 4 次训练周期。
训练样本总数：1.5 亿个样本，训练时间约为 24–36 小时。

训练环境为cassie-mujoco-sim

Single-Gait Policy Results

从最基础的“单一行为控制”入手，即训练策略生成某一种固定的步态，如行走、跳跃或奔跑。这一目标可以通过以下方式轻松实现：

固定相位比（r）：控制 swing/stance 比例，决定机器人每一步中空中与落地的时间占比。
固定周期偏移参数（θ_left, θ_right）：定义左右腿相位的时间差。

只要保持这两个参数不变，就能稳定训练出特定风格的步态。例如：

步态类型	特征参数	训练表现
跳跃 hopping	θ 左右接近，r 高	快速收腿、高空弹跳
行走 walking	θ 左右交错，r 中	中速交替移动
奔跑 running	θ 左右交错，r 高	快速对称步伐
小跑 skipping	θ 左右适中，r 中	弹跳中略显轻盈