【灵巧手抓握】GraspTTA算法学习：GraspCVAE、ContactNet基于物理一致性的抓握姿态生成——Hand-Object Contact Consistency Reasoning

论文题目：《Hand-Object Contact Consistency Reasoning for Human Grasps Generation》

论文链接：https://openaccess.thecvf.com/content/ICCV2021/papers/Jiang_Hand-Object_Contact_Consistency_Reasoning_for_Human_Grasps_Generation_ICCV_2021_paper.pdf

源码链接：https://hwjiang1510.github.io/GraspTTA

论文出处：ICCV21

关键模块：GraspCVAE、ContactNet

背景

任务设置

  给定世界坐标中的3D物体，生成3D人手来抓握他，具体如图1所示。这类任务要比预测具有平行钳口的夹持器难得多：

• 人类手具有更多的自由度，这会导致更复杂的接触情况；
• 生成的抓握动作不仅要在物理上合理，还需要以自然的方式呈现，即与通常抓握物体的方式一致；

  为了合成物理上合理且自然的抓握姿势，最近的研究使用大规模数据集和受监督的生成模型，其中包含抓握注释和手部接触分析。具体而言，大规模数据集允许模型生成逼真的人类抓握动作，接触分析鼓励手部接触点靠近物体，但不互相穿透。虽然这些方法在 对手及其接触点进行建模 方面取得了一定的研究进展，但是他们忽略了物体本身还有更多可能需要接触的区域。

主要思想

  在本文中，作者认为手部接触点和物体接触区域达到相互一致对于抓握的生成至关重要。为了实现这一点，作者提出将两个独立的模型统一起来，用于手部抓握合成和物体接触图估计，作者证明了手部接触点和物体接触图之间的一致性约束不仅有助于在训练期间优化模型得到更好的抓握姿态，而且这种约束还提供了一个自监督任务，在测试期间可以对新物体调整抓握姿态。

  首先，训练一个基于条件变分自动编码器（CVAE）的网络，该网络以3D物体点云作为输入，并预测由MANO模型参数化的手部抓握姿态，即GraspCVAE。在训练期间，作者设计了两个新的损失，一个鼓励手触摸物体表面，另一个迫使真实手触摸的物体接触区域靠近预测的手（手的位置由预测的姿态决定，也就是让物体接触面标签靠近手部）。通过这两个一致性损失，算法可以得到更真实和物理上更合理的抓握姿态。

  其次，给定手的抓握姿势和物体点云作为输入，我们训练另一个网络来预测物体上的接触图，作者将这个模型命名为ContactNet，ContactNet的关键作用是在测试过程中，即在没有真实抓握情况的下提供监督信息，用于微调GraspCVAE。我们设计了一个自监督一致性任务，该任务要求GraspCVAE产生的手部接触点与ContactNet预测的物体接触图一致。我们使用这个自监督任务执行测试过程中的自适应调整，从而微调GraspCVAE，用于生成更好的人类抓握。这种自适应方法可以应用于每个单独的测试实例，并且这一过程不需要任何额外的外部监督，可以灵活地让算法适应不同的输入。

  本文的贡献可以总结为：

• 用于学习人类抓握生成的新型手-物体接触一致性损失；
• 基于一致性约束的新型自监督任务，允许在测试期间调整生成模型；
• 在域内和域外抓握生成方面均有显著的改进。

方法

为了更方便地表述，本节均用第一人称描述。

  我们的目标是根据物体的点云数据作为输入，生成人类抓握的手部网络（hand mesh），生成的手部网络不仅需要以自然逼真的方式呈现，还应以物理上合理的方式紧紧握住物体，我们强调，确保物体和合成手之间的合理接触是获得高质量和稳定的人类抓握的关键。为了解决这个问题，我们建模了双手和物体之间的接触情况，并确保他们彼此的一致性，根据这一约束来改进灵巧手的抓握情况。如图2所示，我们提出了两个网络，一个是生成式GraspCVAE，用于合成抓握手部网络，另一个是ContactNet，用于对物体上的接触区域进行建模。

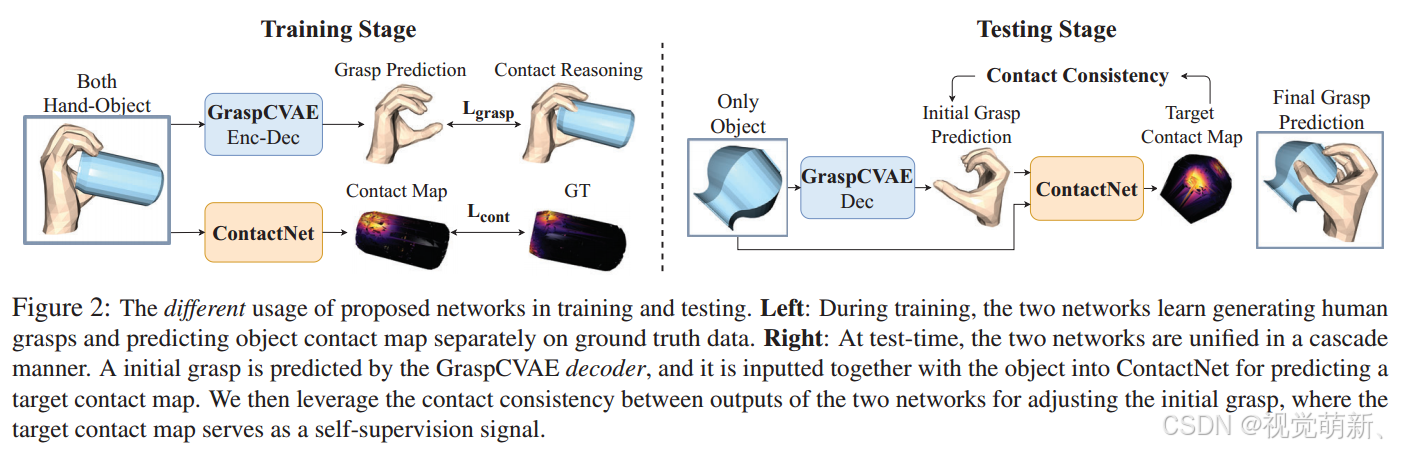
训练阶段

​  如图2左侧所示，我们分别使用真实情况来优化这两个网络，以学习抓握生成和预测物体接触图的能力，在此阶段，GraspCVAE的输入是手和物体，GraspCVAE学习在手的重建范式中合成抓握姿态，这里参考条件变分自动编码器实现这一过程（Conditional Variational Auto-Encoder, CVAE）。为了训练GraspCVAE，我们提出了两种新的损失来确保手与物体接触的一致性，一种损失迫使先前的手部接触顶点靠近物体的表面，另一种损失鼓励物体的公共接触区域同时被手触摸，在训练过程中，物体和生成的手将通过这两种损失在接触形式上找到相互之间的一致性。对于ContactNet的训练，我们采用真实标签来训练模型的接触图预测能力。

测试阶段

  如图2右侧所示，我们将两个网络统一起来，并利用他们输出之间的一致性设计一个自监督任务。给定一个测试对象，我们首先从GraspCVAE解码器（不带编码器）生成初始抓握。之后，将生成的抓握与对象一起传入ContactNet来预测目标接触图，由于ContactNet是使用真实的抓握数据训练得到的，由于手和物体之间不存在穿透，手紧密接触物体表面，他可以模拟理想的手物接触模式（因为测试阶段没有抓握标签，所以无法得到真实的接触面热图，只能通过ContactNet预测）。我们使用来自ContactNet的预测接触图作为微调和优化GraspCVAE生成的抓握目标。如果从GraspCVAE正确预测抓握，则预测抓握的对象接触区域应与目标对象的接触图一致。我们使用这种一致性作为自我监督信号，以适应GraspCVAE在测试期间生成的抓握动作。

GraspCVAE

  GraspCVAE是一个基于条件变分自动编码器（CVAE）的生成网络，它使用条件信息来控制生成，对于GraspCVAE，条件信息是目标的点云数据。在训练阶段，GraspCVAE的编码器和解码器都用于以手部重建的方式学习抓握生成任务，将手部和物体都作为输入；在测试阶段，只使用解码器生成人类对物体的抓握，仅使用3D物体作为输入（不使用抓握作为输入），网络架构如图3所示。

在训练期间

  给定手部点云${\mathcal{P}}^h\in {\mathbb{R}}^{778\times 3}$和物体点云${\mathcal{P}}^o\in {\mathbb{R}}^{N\times 3}$（其中$N$是点数）作为模型的输入，使用两个独立的PointNet分别提取他们的特征，表示为${\mathcal{F}}^h,{\mathcal{F}}^o\in {\mathbb{R}}^{1024}$，之后将这两个特征连接为${\mathcal{F}}^{ho}$，作为GraspCVAE编码器的输入，编码器的输出是后验高斯分布$Q(z|\mu ,{\sigma }^2)$的均值$\mu \in {\mathbb{R}}^{64}$和方差${\sigma }^2\in {\mathbb{R}}^{64}$。为了重建手，我们首先从分布中采样一个潜在代码（latent code）$z$，后验分布确保采样的潜在代码$z$与输入的手部物体相对应。

  解码器将潜在代码$z$和对象特征${\mathcal{F}}^o$的连接作为输入，用于重建手部网格，该网格可以由微分模型MANO表示。MANO模型由形状参数$\beta \in {\mathbb{R}}^{10}$（表示特定于人手的手部形状）和姿势参数$\theta \in {\mathbb{R}}^{51}$（用于表示关节轴角旋转和根关节平移）参数化。给定来自解码器的预测参数$(\hat{\beta },\hat{\theta })$，MANO模型形成一个可微分层，该层输出手的形状：
$$\hat{\mathcal{M}}=(\hat{\mathcal{V}}\in {\mathcal{R}}^{778\times 3},\hat{F})$$
其中$\hat{\mathcal{V}}$和$\hat{F}$分别表示网格的顶点和面，GraspCVAE中的编码器和解码器都是由多层感知机MLP组成。

测试阶段

  测试阶段仅利用GraspCVAE的解码器进行推理，仅给定提取的对象点云特征特征${\mathcal{F}}^o$和从高斯分布中随机采样的潜在代码$z$作为输入，解码器将生成MANO模型的参数，从而得到手部网络的输出。

优化目标

  第一个优化目标是网格的重建误差，他定义在网格的顶点和MANO模型的参数上，我们采用$L_2$距离来计算误差，我们将预测顶点和真实标签之间的重建损失表示为：
$$L_{\mathcal{V}}=||\hat{\mathcal{V}}-{\mathcal{P}}^h|{|}_2^2$$
MANO参数上的损失与该损失定义方式类似，都是距离损失，分别表示为$L_{\theta }$和${\mathcal{L}}_{\beta }$，重建损失可以表示为：
$$L_{\mathcal{R}}={\lambda }_{\mathcal{V}}\cdot L_{\mathcal{V}}+{\lambda }_{\theta }\cdot L_{\theta }+{\lambda }_{\beta }\cdot L_{\beta }$$
​ 第二个优化目标参考VAE的训练过程，定义了一个新的损失，强制潜在潜在代码$z$的分布$Q(z|\mu ,{\sigma }^2)$接近标准高斯分布，通过最大化KL散度来实现这一目的，即：
$$L_{\mathcal{K}\mathcal{L}\mathcal{D}}=-KL(Q(z|\mu ,{\sigma }^2)||\mathcal{N}(0,I))$$
  最后，我们还鼓励抓握在物理上具有合理性，即物体和手不应该相互渗透（即不能穿模），我们将手内部的点云子集表示为${\mathcal{P}}_{in}^o$，渗透损失定义为最小化他们到最近手部顶点的距离：
$$L_{penetr}=\frac{1}{|{\mathcal{P}}_{in}^o|}\sum _{p\in {\mathcal{P}}_{in}^o}\underset{i}{\min }||p-{\hat{V}}_i|{|}_2^2$$
  总损失可以表示为：
$$L_{base}=L_{\mathcal{R}}+{\lambda }_{\mathcal{K}\mathcal{LC}}\cdot L_{\mathcal{K}\mathcal{LC}}+{\lambda }_p\cdot L_{penetr}$$

ContactNet

  基线框架中存在两个潜在的挑战：

• 基线模型中的损失忽略了手与物体之间的物理接触，无法确保抓取过程中的稳定性；
• 抓握生成是多模态的（抓握姿态存在多峰概率分布问题），真实的手势并不是唯一的答案，有可能存在多种抓取姿态；

为了应对这些挑战，我们从手和物体两个方面设计了两种新颖的损失，用于得到合理的手与物体之间的接触面，并找到他们之间的相互一致性。

以物体为中心的损失

  从物体的角度来看，有些区域经常被人用手接触。我们使用以物体为中心的损失来鼓励人手靠近这些区域。具体地来说，从真实的手与物体之间的相互作用中，我们可以通过使用函数$f(\cdot )$对物体的所有点与其最近的手部先验顶点之间的距离$D({\mathcal{P}}^o)$进行标准化（normalizing）来推导出物体的接触图$\Omega \in {\mathbb{R}}^N$：
$$f(D({\mathcal{P}}^o))=1-2\cdot (Sigmoid(2D({\mathcal{P}}^o))-0.5)$$
归一化接触图案例如下图所示，接触图得分范围为$[0,1]$。

  这种标准化有助于网络关注靠近手的物体区域，之后我们使用损失函数强制从生成的手计算出的物体接触图$\hat{\Omega }$靠近标签接触图：
$$L_{\mathcal{O}}=||\hat{\Omega }-\Omega |{|}_2^2，\Omega =f(D({\mathcal{P}}^o))$$
这一损失用于优化ContactNet。

以手为中心的损失

  我们定义先前的手部接触顶点${\mathcal{V}}^p$，具体如下图所示。

  给定手部接触顶点的预测位置，我们将附近的物体点作为可能的接触点。具体地来说，对于物体上的每个点${\mathcal{P}}_i^o$，我们计算距离：
$$D({\mathcal{P}}_i^o)=\underset{j}{\min }||{\mathcal{V}}_j^p-{\mathcal{P}}_i^o|{|}_2^2$$
如果它小于阈值，我们将其视为物体上的可能接触点，我们以手为中心损失的目标是将手部接触顶点推进物体上所有可能的接触点，也就是尽可能减小这段距离：
$$L_{\mathcal{H}}=\sum _{i}D({\mathcal{P}}_i^o),D({\mathcal{P}}_i^o)\le \mathcal{T}$$
其中阈值$\mathcal{T}$为1cm，抓取总损失可以表示为：
$$L_{grasp}=L_{baseline}+{\lambda }_{\mathcal{H}}\cdot L_{\mathcal{H}}+{\lambda }_{\mathcal{O}}\cdot L_{\mathcal{O}}$$
其中，${\lambda }_{\mathcal{H}}$和${\lambda }_{\mathcal{O}}$为平衡损失的权重。直观地看，$L_{\mathcal{O}}$通常回答“在哪里抓握？”的问题，并且不指定哪个手应该靠近物体的接触区域，而$L_{\mathcal{H}}$用于动态地找到“哪个手指应该接触？”的答案，通过这两个提出的损失，手部接触点和物体接触区域将相互一直，从而产生稳定的抓握。

ContactNet的学习

  ContactNet用于建模手与物体之间的接触信息，具体如下图所示。

  网络的输入是手和物体的点云，输出是$N$个物体点的物体接触图，表示为${\Omega }^c\in {\mathbb{R}}^N$，我们使用两个PointNet编码器来提取手和物体的特征图，由于我们需要预测每个点的接触分数（${\Omega }_i^c$为${\mathcal{P}}_i^o$），因此不能破坏点云的三维空间关系，为了保证特征与点的对应关系，我们利用PointNet编码器中物体的局部点云特征${\mathcal{F}}^s\in {\mathbb{R}}^{N\times 64}$来执行后续的计算。除此之外，我们还使用手和物体的全局特征，首先将他们相加，之后复制$N$次，并将其与物体局部特征连接起来，形成一个${\mathbb{R}}^{N\times 1024}$维的特征图。给定这些特征，我们在顶部层应用四层1-D卷积来回归由Sigmoid函数激活的物体接触图，训练损失是预测的接触图${\Omega }^c$和标签$\Omega$之间的$L_2$距离，即：
$$L_{cont}=||{\Omega }^c-\Omega |{|}_2^2$$
注：在训练期间，ContactNet的输入直接从标签数据中获得。

测试时的接触图自适应调整

  在测试过程中，我们以级联的方式结合GraspCVAE和ContactNet，如图2右侧所示。给定物体点云当做输入，GraspCVAE首先生成手部网格（mesh）$\hat{\mathcal{M}}$作为初始抓握。在有了物体点云分布和手部抓取姿态之后，我们相应地可以计算器物体接触图${\Omega }_{\hat{\mathcal{M}}}$。之后，将预测的手部网格和物体点云作为输入，ContactNet将预测另一个接触图${\Omega }^c$，如果抓握预测正确，则两个接触图应该是一致的。基于这一思想，我们将自监督一致性损失定义为：
$$L_{refine}=||{\Omega }_{\hat{\mathcal{M}}}-{\Omega }^c|{|}_2^2$$
该损失用于微调GraspCVAE，除了这种一致性损失之外，我们还结合了以手为中心的损失$L_{\mathcal{H}}$和穿透损失$L_{penetr}$，从而确保抓握在物理上是合理的，我们将所有三个损失的联合优化应用于单个测试示例，如下图所示：
$$L_{TTA}=L_{refine}+{\lambda }_{\mathcal{H}}\cdot L_{\mathcal{H}}+{\lambda }_p\cdot L_{penetr}$$
我们使用这个损失去更新GraspCVAE解码器，并冻结网络的其他部分。

实验

评测指标

• 穿透（Penetration）：通过测量物体与生成的抓握之间的穿透深度和体积得到；
• 抓握位移（Grasp displacement）：用于策略抓握的稳定性，将物体和生成的抓握放入模拟器中，模拟器会计算抓握下，物体的运动情况。具体地来说，指尖上的力与穿透体积正相关，模拟器通过计算指尖上的力，再结合物体自身的中立，就可以模拟出物体中心的位移，进一步评估出抓握的稳定性；
• 感知分数（Perceptual score）：用于评估生成的抓握自然度，利用Amazon Mechanical Turk进行评估；
• 手-物体接触指标（Hand-object contact metrics）：用于分析手与物体之间的接触。计算样本级手与物体的接触率、单个物体和手的接触点率和接触物体的手指分数，通过判断物体一个点到另一个点云中最近邻的距离是否小于0.5cm来判断该点的接触状态，同时还计算物体接触图得分，为$s=100\cdot \frac{\sum \Omega }{N}\in [0,100]$，该接触图反应了抓握的覆盖面积，通常接触面积越大，意味着抓握越好；

实验结果

​  算法在三个数据集下的评测指标如下表所示：

注：以上仅是笔者个人见解，若有问题，欢迎指正。