算法导论 实验三 快速排序及其优化

---

一、实验目的

1、 理解快速排序的概念和基本思想
2、 了解适用快速排序的问题类型，并能设计相应的快速排序算法
3、 掌握快速排序算法时间复杂度分析，以及实际问题复杂性分析方法

二、实验内容

当输入基本有序时，插入排序的运行速度很快。在实际应用中，我们可以利用这一特性来提高快速排序的速度。在对一个长度小于k的子数组调用快速排序时，让它不做任何操作就返回。当上层的快速排序调用返回后，再对整个数组运用插入排序来完成排序过程。

三、实验要求

（1）描述问题的输入与输出；
（2）请描述所设计算法解决问题的设计思路，并写出所设计算法的伪代码；
（3）用高级编程语言实现算法，并通过问题实例测试程序，对运行结果截图；
（4）分析所设计算法的时间复杂度；
（5）进行实验分析总结，撰写实验报告。
（6）这一排序的时间期望复杂度应该为O(nk+nlg(n/k))
要求：不允许直接调用库函数来排序，例如c++的sort()
说明：
结果单位为ms，使用双精度浮点数存储，计时开始的标志是进入排序之前的语句

四、算法设计与分析

（1）输入：大小为n的一维数组A[0…n-1]，数组的边界下标及一个整数值k（k不大于n）
（2）输出：输入序列的一个排列，元素按从小到大的顺序排列
（3）算法思路：
先对整个数组进行快速排序，递归调用快排，当子数组的长度小于k时递归终止。快排调用全部返回后再对整个数组进行插入排序，即可得到排序好的数组。详细设计见伪代码，需要对基本的快速排序上加上限制条件。
①　调用快速排序
②　若l-r小于k，则返回调用
③　选定基准点x，将小于等于x的元素移动到左边，大于的移动到右边
④　递归调用快排，排序x左边的子数组
⑤　递归调用快排，排序x右边的子数组
⑥　对整体数组使用插入排序
（4）伪代码：

Partion(A,l,r)
1	x = A[r];
2	i = l-1;
3	for j=l to r-1 
4		if  A[j] <= x
5			i=i+1
6			Swap A[i] with A[j]
7	Swap A[i+1] with A[r]
9	return i+1

Quick_Sort2(A,l,r,k)
1	//长度小于k的子数组调用快速排序时，让它不做任何操作就返回
2	if  r-l+1<k
3		return
4	else
5		d = Partion(A,l,r)
6		Quick_Sort2(A,l,d-1,k)
7		Quick_Sort2(A,d+1,r,k)

Optimized_QuickSort(A,l,r,k)
1	Quick_Sort2(A,l,r,k)
2	Insertion_Sort(A,l,r)

五、详细设计与实现

普通快排与优化后的快排的比较方法：
采用c++提供的clock函数来计算普通快排和优化后的快排的运行时间（ms）来比较两者
1.随机产生大小为n的数组，即使产生最坏的情况，由于普通快排和优化后的快排都使用的同样的数组，仍能反映出普通快排和优化后的快排的性能差别。
2.不同k下，普通快排和优化后的快排都使用1产生的同一个数组，这样方便比较不同k下优化后的快排性能
3.同时，不同k下，普通快排和优化后的快排都重复运行五次，取平均值，减少机器因素带来的误差
4.由于k的范围取的较大时，随着n的增大，运行速度会非常慢，考虑到理论上k取到logn时有最佳性能，由由于本次最大输入规模为1000000，所以k取到150即可满足观察的范围。
（1）主要实现代码：
见附录
（2）画图代码：
见附录
（3）运行结果：
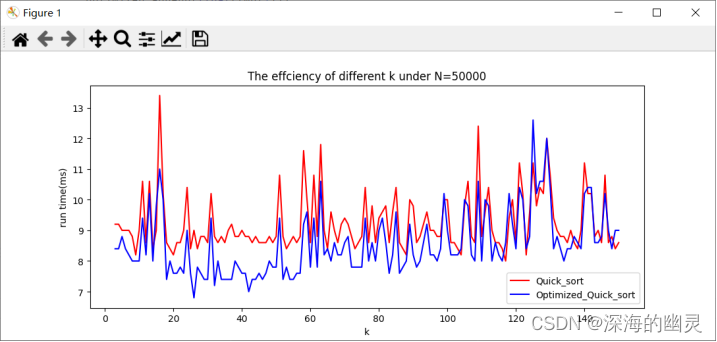
【1】数据规模为50000

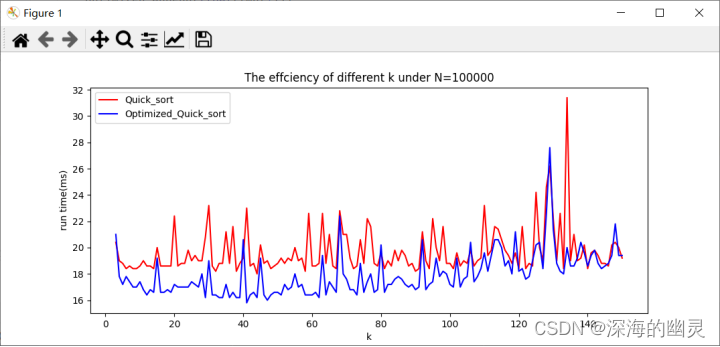
【2】数据规模为100000

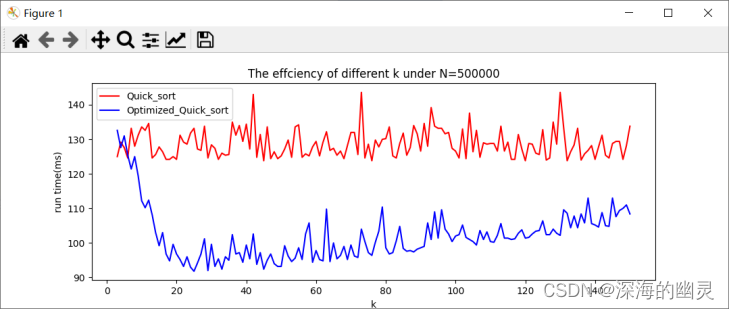
【3】数据规模为500000

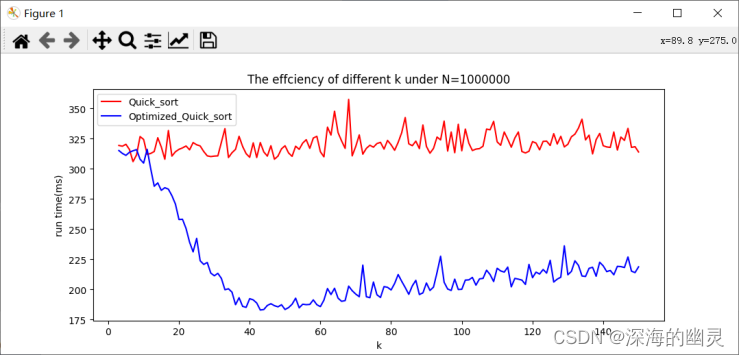
【4】数据规模为1000000

（4）时间复杂度分析：

对于k的取值，粗略分析下，直观上nk小于等于nlgn时，优化后的快排期望时间复杂度要比普通快排的期望时间复杂度小。因为nk越接近nlgn总的期望时间复杂度和普通快排没有明显的优化，所以直观理论上k<=lgn。而且k越大越好，因为nlgn/k的影响比nk更强，k越大，nlgn/k越小。所以理论上，k取lgn附近是最优的。（这里的分析是不严谨的，总结中有探讨）

六、结果分析

1.从结果可以看出，整体上优化的快排要比普通快排运行时间快。
2.随着数据规模的增大以及k的增大，优化后的快排运行时间比普通快排的运行时间差距越明显，更快直到超过特定的k值后差距又在缩小。
3.普通快排在输入规模相同的时候运行时间有波动的原因是机器因素（进程的调度，cpu的占用等），相同程序在同数据每次运行的时间实际上是不同的，尤其是精细到ms级别时可以看到有较明显的波动。本实验对每次的运行都采取了5次重复取平均的方法所以波动看起来并不是很大，若不采取时波动更加大。
4.可以看到随着规模的增大，优化后的快排取到最小值的k值在不断增大。但并不是准确在lgn附近，比如数据规模在1000000时，理论k=lg1000000，约为20，但实际上在k=44处有最小值。
5.数据规模小时，优化后的快排对于k的取值上呈现极值的趋势并不明显，而且超过一定k后甚至运行时间没有普通快排优秀。同样可以看到=据规模大时，k取到150以上后的趋势预测，也会在一点开始比普通快排运行时间大。

七、总结

1.整体上优化后的快排比普通快排运行时间少，且会呈现先下降到极值后再上升的趋势，当k取很大时优化后的快排不比普通快排优秀。
2.在实践中，发现k的取值并不是在lgn附近时有最佳运行时间（大多数情况是比lgn大），原因是理论分析时忽略了常数因子带来的影响，而实际运行中这些常数不能忽略，k应根据实验结果进行选择。
关于k的取值，网上考察结果也如下：

（出自https://walkccc.me/CLRS/Chap07/7.4/）
从以上推导中发现，k的选择与两种排序算法时间复杂度中的常数因子相关。若快排的时间复杂度中的常数因子Cq比插排常数因子Ci越大，那么k也应当越大。反之，k应当越小。

---

附录：
1.主要代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <ctime>
#include <fstream>

using namespace std;

//打印数组 
void print_a(int A[],int l,int r){
	for (int i=l;i<=r;i++){
		cout << A[i] << " ";
	}
	cout << endl;
}

//产生随机数组,整数范围在1~100000 
int* Create_RandA(int n)
{
	int* A = new int[n];
	for (int i=0;i<n;i++){
		A[i] = rand()%100000+1;
	}
	return A;
}


//basic快排 

int Partion(int A[],int l,int r)
{
	int x = A[r];
	int i = l-1;
	for (int j=l;j<=r-1;j++){
		//当j碰到大于x的会继续走下去，即i前的为大于x的 
		if (A[j] <= x){
			i++;
			swap(A[i],A[j]);
		}
	}
	swap(A[i+1],A[r]);
	return i+1;
}


void Quick_Sort(int A[],int l,int r)
{
	if (l>=r){
		return;
	}
	else{
		int d = Partion(A,l,r);
		Quick_Sort(A,l,d-1);
		Quick_Sort(A,d+1,r);
	}
}

//basic插排
void Insertion_Sort(int A[],int l,int r)
{
	for (int i=l+1;i<=r;i++){
		int key = A[i];
		int j = i-1;
		while (j>=0 && A[j]>key){
			A[j+1]=A[j];
			j--;
		}
		A[j+1] = key;
	}
} 


//用于下面的优化后的快排 
void Quick_Sort2(int A[],int l,int r,int k)
{
	//长度小于k的子数组调用快速排序时，让它不做任何操作就返回
	if (r-l+1<k){
		return;
	}
	else{
		int d = Partion(A,l,r);
		Quick_Sort2(A,l,d-1,k);
		Quick_Sort2(A,d+1,r,k);
	}
}


//optimized快排
void Optimized_QuickSort(int A[],int l,int r,int k)
{
	Quick_Sort2(A,l,r,k);
//	print_a(a,l,r);
	Insertion_Sort(A,l,r);
} 


//复制数组
int* Copy_a(int A[],int n)
{
	int* a = new int[n];
	for (int i=0;i<n;i++){
		a[i] = A[i];
	}
	return a;
} 


//结果写入csv
void Write2csv(string path,double res_quick[],double res_opt[],int m)
{
	ofstream outFile; // 创建流对象
	outFile.open(path, ios::out); // 打开文件
	for (int i = 0; i < m; i++)
	{
		outFile << res_quick[i]<<','<< res_opt[i]<<',';
		outFile << endl;
		
	}
	outFile.close(); // 关闭文件
}


int main()
{
	srand(99);
	//随机数组大小 
	int n; 
	cin >> n;

	
	int m = 150-3+1;
	double res_optimized[m];
	double res_quick[m];
	clock_t start,finish;
	double t_quick,t_opt;
	int t,tmp;
	
	int* original = Create_RandA(n);
	//k<=2时调用一次快排就排好了，没有意义，所以从k=3开始
	//期望是k=n**0.5时有最佳效果，由于k=50时，2**k已经达到达1.12e15足够大,这里为了进一步观察k的变化设为100 
	for (int k=3;k<=150;k++){
		
		//相同输入下重复五次取平均,减少机器因素 
		t = 5;
		tmp = t;
		t_quick = 0.0;
		t_opt = 0.0;
		while(tmp--){
			
			//普通快排
			int* a = Copy_a(original,n);
			start=clock();
			Quick_Sort(a,0,n-1);
			finish=clock();
			t_quick+=(double)(finish-start);
			delete []a;
			
			//优化后的快排 
			int* b = Copy_a(original,n);
			start=clock();
			Optimized_QuickSort(b,0,n-1,k);
			finish=clock();
			t_opt+=(double)(finish-start);
			delete []b;
		} 
		res_quick[k-3] = t_quick/t;
		res_optimized[k-3] = t_opt/t;
		cout <<k-3<<": "<< res_quick[k-3] <<" "<< res_optimized[k-3]<< endl;
	} 
	Write2csv("D:\\算法设计与分析\\实验3\\res_1000000.csv",res_quick,res_optimized,m);
	return 0;
} 

2.画图代码：

import matplotlib.pyplot as plt
import math

def Loader(filepath):
    quick = []
    optimized = []
    with open(filepath) as f:
        for line in f.readlines():
            tmp = line.strip().split(',')
            quick.append(float(tmp[0]))
            optimized.append(float(tmp[1]))
    return quick,optimized

if __name__=='__main__':
    path = r'D:\算法设计与分析\实验3\res_1000000.csv'
    quick,optimized= Loader(path)
    k = range(3,len(quick)+3)
    plt.figure()
    plt.plot(k, quick, label='Quick_sort',color='r')
    plt.plot(k, optimized, label='Optimized_Quick_sort',color = 'b')
    plt.xlabel('k')
    plt.ylabel('run time(ms)')
    plt.legend()
    plt.title('The effciency of different k under N=1000000')
    plt.show()