深度探索：机器学习中的高斯过程回归（Gaussian Process Regression, GPR）算法原理及其应用

最新推荐文章于 2025-04-18 19:29:52 发布

生瓜蛋子

最新推荐文章于 2025-04-18 19:29:52 发布

阅读量7.9k

点赞数 20

分类专栏：机器学习文章标签：机器学习算法回归

本文链接：https://blog.csdn.net/qq_51320133/article/details/137991515

版权

机器学习专栏收录该内容

154 篇文章

订阅专栏

本文详细介绍了高斯过程回归的理论基础、算法原理，包括建模、学习和预测过程。讨论了其优点（如不确定性量化、非参数性和平滑性）及缺点（计算复杂度和超参数选择），并通过案例展示了在医药、金融和工业领域的应用，并与其他算法进行了对比。未来，随着计算技术的发展，高斯过程回归有望在更多领域发挥重要作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 引言与背景

高斯过程回归（Gaussian Process Regression, GPR）是一种基于高斯过程理论的非参数机器学习方法，尤其适用于回归分析任务。它以其强大的建模能力和对不确定性量化的优势，在诸多领域如生物医药、金融预测、地质勘探、计算机视觉等得到了广泛应用。本文将详细阐述GPR的理论基础、算法原理、实现细节、优缺点分析、实际应用案例，以及与其它回归算法的对比，并对未来发展进行展望。

2. 高斯过程与高斯过程回归定理

高斯过程是一种定义在无限维空间上的随机过程，其任意有限子集的联合分布都为高斯分布。每个高斯过程由其均值函数 $m(\cdot )$ 和协方差函数 $k\left ( \cdot ,\cdot \right )$ 完全确定，其中均值函数刻画了过程的整体趋势，协方差函数描述了过程在不同位置之间的相关性。

高斯过程回归定理：假设观测数据集 $D=\left \{ \left ( x_{i},y_{i} \right ) \right \}_{i=1}^{N}$ ，其中 $x_{i}$ 为输入， $y_{i}$ 为输出。若观测噪声ϵ独立同分布且服从均值为0、方差为 $\sigma _{n}^{2}$ 的正态分布，且函数 $f\left ( x \right )$ 服从均值为 $m\left ( x \right )$ 、协方差为 $k\left ( x,x{}' \right )$ 的高斯过程，则给定观测数据集，新观测点 $x_{*}$ 的输出 $y_{*}$ 服从高斯分布：

其中，

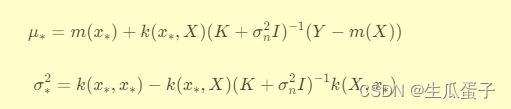
这里， $K= k\left ( X,X \right )$ 是协方差矩阵，Y是观测输出向量， $m\left ( x \right )$ 和 $m\left ( x_{*} \right )$ 分别是均值函数在数据点和新点上的值， $k\left ( x_{*},X \right )$ 和 $k\left ( X,x_{*} \right )$ 是协方差函数在新点和数据点间的计算结果。

3. 算法原理

a) 建模：高斯过程回归通过定义高斯过程的均值函数和协方差函数来构建模型。均值函数通常设置为常数（如0）或简单函数（如线性函数），而协方差函数（核函数）的选择更为关键，常见的有RBF（径向基函数）、Matérn核、周期核等，它们通过调整超参数来适应数据的不同特性。

b) 学习：给定观测数据集，利用高斯过程回归定理，可以计算出新点 $x_{*}$ 的预测均值 $\mu _{*}$ 和方差 $\sigma _{*}^{2}$ ，即预测值及其不确定性。此外，通过对协方差矩阵K求逆（或使用Cholesky分解、Woodbury公式等方法加速计算），可以得到高斯过程的后验分布，进而进行参数优化（如最大似然估计、变分推理）。

c) 预测：对于新输入数据，利用已学习的高斯过程模型，计算其预测均值和方差，得到预测结果及其不确定性。

4. 算法实现

以下是一个使用Python和sklearn库实现高斯过程回归的基本示例，并附带详细讲解：：

Python

import numpy as np
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 生成模拟数据集
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 1)  # 一维输入特征
y = np.sin(10 * X) + np.cos(5 * X) + np.random.normal(scale=0.1, size=n_samples)  # 添加噪声的目标变量

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 定义高斯过程回归模型和核函数
kernel = RBF(length_scale=1.0, length_scale_bounds=(1e-1, 10.0))  # 使用RBF核函数，并设置长度尺度的搜索范围
gpr = GaussianProcessRegressor(kernel=kernel, alpha=1e-½, optimizer='fmin_l_bfgs_b', n_restarts_optimizer=10)

# 训练模型
gpr.fit(X_train, y_train)

# 预测测试集结果
y_pred, y_pred_std = gpr.predict(X_test, return_std=True)  # 获取预测均值和标准差（方差的平方根）

# 计算并打印预测误差
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error (MSE): {mse:.2f}')

# 可视化结果
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 6))
plt.plot(X_train, y_train, 'o', color='gray', label='Training Data')
plt.plot(X_test, y_test, '^', color='black', label='True Values')
plt.plot(X_test, y_pred, '-', color='red', label='Predictions')
plt.fill_between(X_test.ravel(), 
                 y_pred - y_pred_std, 
                 y_pred + y_pred_std, 
                 alpha=0.2, color='pink',
                 label='Standard Deviation')

plt.title('Gaussian Process Regression with RBF Kernel')
plt.xlabel('Input Feature')
plt.ylabel('Target Variable')
plt.legend()
plt.show()

代码讲解：

导入所需库：
- numpy用于生成模拟数据和数值计算。
- sklearn.gaussian_process包含高斯过程回归模型。
- sklearn.gaussian_process.kernels提供多种核函数。
- sklearn.model_selection.train_test_split用于划分训练集和测试集。
- sklearn.metrics.mean_squared_error计算均方误差（MSE）。
生成模拟数据集：
- 生成100个一维随机输入特征X。
- 设置目标变量y为输入特征的复合非线性函数（包含噪声），模拟真实世界中的复杂关系。
数据集划分：
- 使用train_test_split将数据集划分为80%作为训练集和20%作为测试集。
定义高斯过程回归模型：
- 使用GaussianProcessRegressor类创建模型实例。
- 选择RBF（径向基函数）核函数，并设置初始长度尺度为1.0，同时指定长度尺度的搜索范围（用于超参数优化）。
- 设置alpha参数为先验噪声方差（这里取0.5），用于平衡数据拟合与模型平滑度。
- 使用fmin_l_bfgs_b优化器进行超参数优化，并设置n_restarts_optimizer为10，表示对优化过程进行10次重启以避免局部最优解。
训练模型：
- 调用gpr.fit()方法，使用训练集数据训练高斯过程回归模型。
模型预测：
- 调用gpr.predict()方法，传入测试集数据，返回预测均值y_pred和标准差y_pred_std。
计算预测误差：
- 使用mean_squared_error计算预测结果与真实值之间的均方误差。
可视化结果：
- 使用matplotlib绘制图表，展示训练数据、真实值、预测值以及预测不确定性的区间（由标准差确定）。

通过上述代码，不仅实现了高斯过程回归算法，还完成了模型训练、预测、误差计算以及结果可视化。这有助于直观地理解高斯过程回归如何拟合数据、预测新点以及量化预测不确定性。

5. 优缺点分析

优点：

不确定性量化：高斯过程回归不仅能提供预测值，还能计算预测的不确定性，这对于决策支持、风险评估等任务至关重要。
非参数性：无需预先设定模型参数数量，能灵活适应数据复杂度，避免过拟合或欠拟合。
平滑性：自然具备平滑预测能力，适用于数据点稀疏或存在噪声的情况。

缺点：

计算复杂度：求解高斯过程回归涉及到协方差矩阵的逆运算，其复杂度为�(�3)O(N3)，对大规模数据集效率较低。
核函数选择与超参数 tuning：选择合适的核函数和超参数对模型性能影响显著，但往往需要领域知识和大量实验。
不适用于大规模分类任务：高斯过程回归主要用于回归任务，尽管可以推广到分类问题，但对于大规模分类任务效率较低。

6. 案例应用

a) 医药研发：在药物发现中，利用GPR预测化合物的生物活性、毒性等性质，辅助筛选候选药物。

b) 金融预测：在股票价格、汇率等金融时间序列预测中，利用GPR模型的不确定性估计，进行风险评估和投资决策。

c) 工业监控：在设备故障预测、质量控制等工业场景，利用GPR模型的平滑性和不确定性估计，提前预警故障，优化生产流程。

7. 对比与其他算法

a) 与线性回归：线性回归模型简单、易于解释，但假设数据呈线性关系，且不能提供不确定性估计。GPR模型更灵活，能处理非线性关系，且能量化预测不确定性。

b) 与决策树、随机森林等：这些模型适用于处理非线性关系，但缺乏平滑性，且难以直接提供不确定性估计。GPR模型在这方面具有优势。

c) 与神经网络：神经网络模型强大、灵活，但需要大量数据和计算资源，且通常通过 dropout、ensemble等方法间接估计不确定性。GPR模型在小数据集和不确定性估计方面更具优势。

8. 结论与展望

高斯过程回归作为一种基于高斯过程理论的非参数回归方法，以其优秀的建模能力、不确定性量化优势，在众多领域展现出广泛的应用价值。尽管面临计算复杂度高、核函数选择与超参数 tuning等问题，但随着计算技术的进步（如GPU加速、分布式计算）和新型核函数的研究（如深度高斯过程、稀疏高斯过程），GPR在处理大规模数据、复杂模型等方面的能力将持续提升。未来，结合领域知识与自动化超参数优化方法，高斯过程回归有望在更多实际问题中发挥关键作用，推动相关领域的智能化发展。