重构大学数学基础_week01_PCA主成分分析

什么是PCA呢？一句话来概括，就是通过基变换用于处理数据降维的方法。首先呢，我们先来对它进行数学推导，然后再解释它的用途。

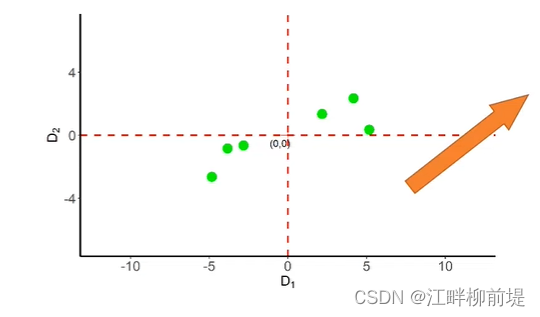
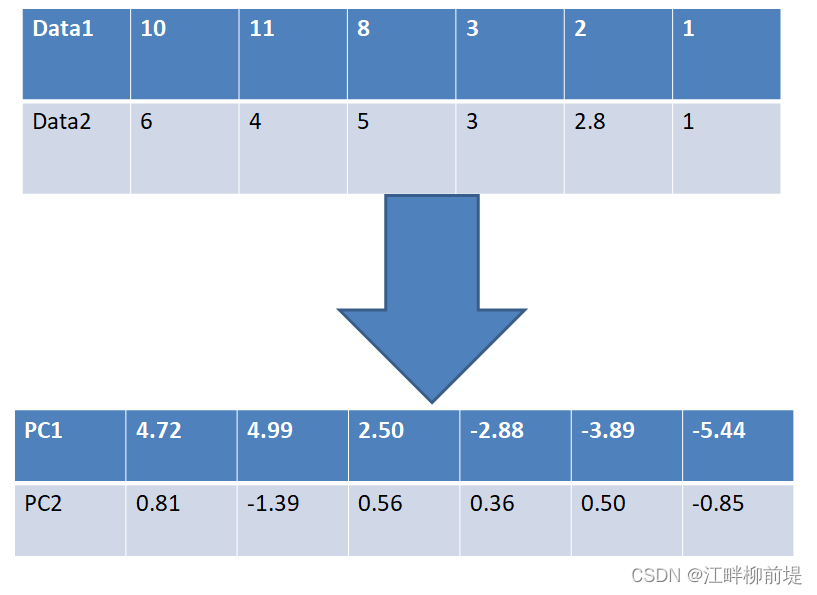
为了说明什么是PCA，我来举一个例子。这是一个二维矩阵，矩阵内部的每个数据在二维空间的坐标如图所示。

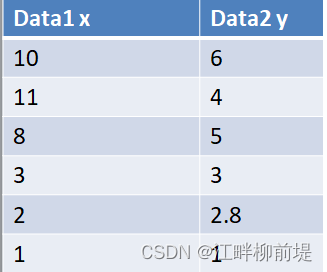
这个矩阵有六行两列，我们以data1为横坐标，data2为纵坐标，就可以把它表示在一个二维平面中。

在开始推导PCA之前，我们首先要对数据零均值化，即让样本数据中心落在原点。如图所示。我们在刚才了解到PCA是一种数据降维的方法，我举的例子是二维的，那么我们就要对它降到一维，并且尽可能多的保留原始数据的信息。因此，我们需要找到一个方向，使得这些零均值化后的数据在这个方向的投影分散得最开。这样一来，

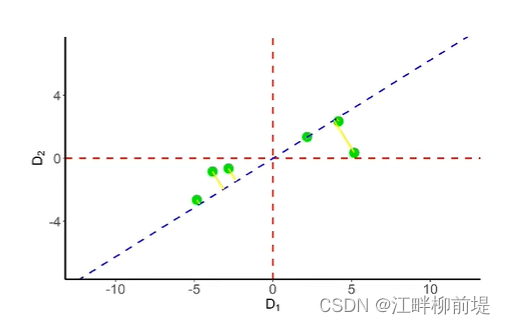
一个毫无头绪的有损降维问题就转化为了求最值的问题，这也是为什么一开始要求均值把中心平移到原点，因为如果中心不固定，那么虽然相对位置不变，但是坐标绝对值不同，就会导致没有办法量化说明点的分散程度。

接下来，我们就要去找这个让点的投影分散得最开的方向。一提到分散程度，那肯定离不开方差。方差的定义就是就是样本点到样本中心距离的平方除以样本数量减一。由于数据处理后的中心是原点，所以Data1和Data2的样本均值都是0，因此，我们可以很方便地得到x轴方向和y方向的方差。

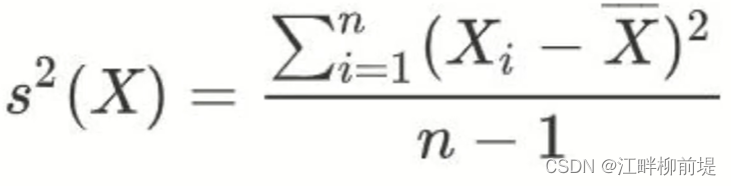
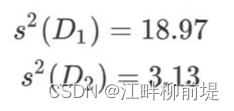
但是，我们可以发现，Data1与Data2并非相互独立，它们间存在一定的正相关关系，就是总体上看X增大，Y也跟着增大。

因此，我们就引入了协方差。 同样的，由于均值我们都化为了0，最终的公式其实也简化成了横纵坐标之积的和除以n-1，这里除n-1是为了无偏估计。

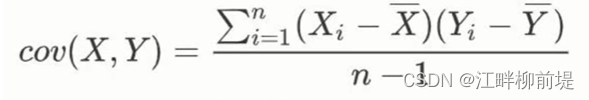
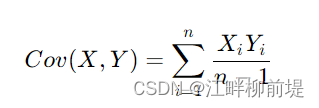
实际上，我们可以用一个协方差矩阵来表示这些结果。对于这个例子而言，协方差矩阵是一个2X2的矩阵。它的元素依次是x轴方向的方差、xy协方差、xy协方差和y轴方向的方差。我们用字母C来表示，即covariance的缩写。如果我们用A来表示将样本中心移至原点后的原始数据矩阵的话，协方差矩阵其实就是A的转置与A的内积除以n-1。

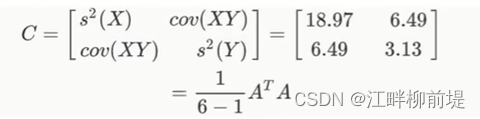
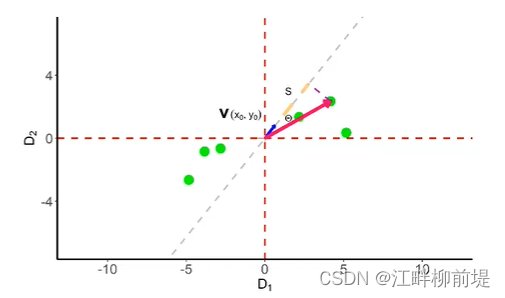
接下来，我们要把它引导到平面某一个单位向量上去。这个单位向量我们命名为v，值是(x0，y0)，其中，x0方加y0方等于1。由于v是一个单位向量，所以某个点的坐标向量与该单位向量的内积，等于该坐标向量的模乘以单位向量的模（就是1）再乘以夹角余弦，即该向量在单位向量上的投影，我们记为S,注意这个S是大写的，要与标准差区分开。

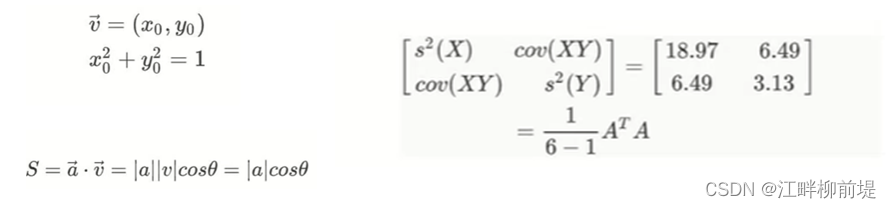
那么，让点分散得最开的方向是否就可以被定义为，所有点在某一方向上投影至中心距离方差最大的方向呢? 也就是要找到S方之和除以n-1最大的方向

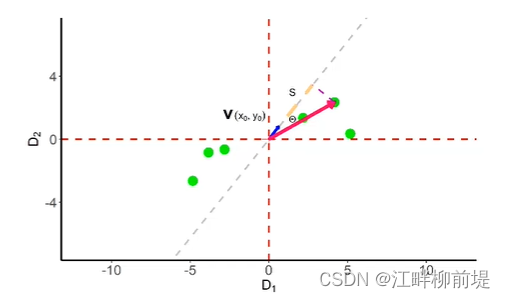
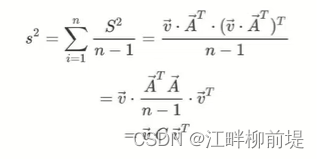
而这个平方和，也可以写作矩阵v乘矩阵A的转置再乘A再乘v的转置并除以n-1的形式。其中，A是我们之前提到过的平移至原点的原始数据矩阵。到了这一步，我们发现中间产生的A的转置乘A除以n-1其实就是我们之前推导过的协方差矩阵C。我们之前费劲计算的表示数据分散程度的协方差矩阵，终于在这一步派上了用场。因此我们用来求最值的核心参数，投影的方差s方，就已经构建完成了。接下来，我们的工作就是求最值。求最值，我们使用的是拉格朗日乘数法。在最优化求解的时候，要求解xxx的最大值，习惯上会乘以一个负数，写成求解负的xxx的最小值,所以最顶上的优化目标应该写成(min J=-s^2)，目标函数是方差s方等于v乘协方差矩阵乘v的转置

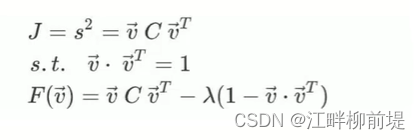
限制条件是，v乘v的转置等于1，因为它是单位向量。由此，构建方程F（V)等于v乘C乘v的转置减去lambda乘（1-v乘v的转置)。方程对v求导，结果是C乘v等于lambda乘v

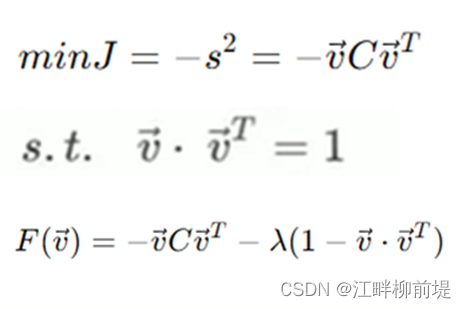
到了这，我们回头看一下可以发现，c一定是对称矩阵，也就一定是方阵。因此,我们可以对其做特征值分解（EVD)，就是求特征值和特征向量。在这个案例中，对C做特征值分解可以得到两个相互独立的特征向量，其中向量vl的转置也就是主成分一(PC1)的方向是-0.94，-0.34，相应的特征值是21.28，PC2的特征向量是0.34，-0.94，特征值是0.81。

为了更好地理解这一结果的几何意义，我们首先淡去原先的坐标轴。然后旋转。这样一来，PC1和PC2就与习惯中的横纵坐标重合了。点集中的每个点都可看作是由PC1和PC2上的投影所构成的。例如点a，它在原先坐标轴中的坐标是(4.17，2.37)

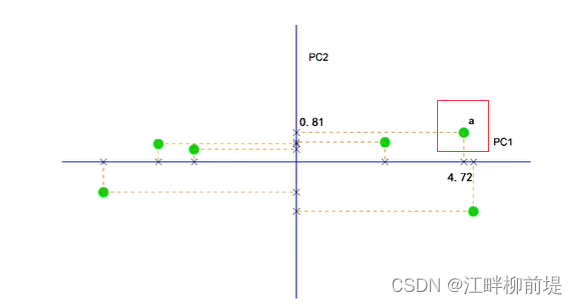
如今在主成分1上的投影长度是4.72，在主成分2上的投影长度是0.81，举得这个例子不太好算啊，4.72=4.17×0.94+2.37×0.34，0.81=4.17×（-0.34）+2.37×0.94。。因此，它既可以理解为由4.17个单位的Data1和2.37个单位的Data2组成，也可以理解为由4.72个单位的主成分1和0.81个单位的主成分2组成。

说完了特征向量，再谈谈特征值吧。这是我们之前计算的投影方差公式。在拉格朗日乘数法最值条件下，它的特征向量恰巧就是向量v的转置，将其化简，我们发现，由于特征向量是单位向量，某一主成分方向上投影的方差，其实就是相应的特征值lambda。由于我们之前用某一方向上数据的分散程度来衡量某主成分的信息量。又赋予了方差s方描述该方向投影分散程度的含义，那么它也就描述了该主成分包含信息的多少。 由此我们计算出了主成分1涵括了总体96.33%的信息，而主成分2只体现了3.67%的信息量。因此我们只需要保留主成分1就可以保留绝大多数信息。

通过以上过程。我们成功地将原有的二维数据转换成了平面点在主成分1上的投影这一一维数据。

以上就是PCA的数学推导，下面我们来看PCA在机器学习领域的相关应用。

数据预处理：在进行机器学习模型训练之前，PCA常被用作数据预处理的一个步骤，通过降维减少计算量和存储需求，同时可能改善模型的训练速度和性能，特别是在处理高维数据集时。

特征选择与抽取：PCA能够帮助识别数据中的主要特征，即那些包含最多信息的维度，从而辅助特征选择。通过保留最重要的主成分，可以去除不重要的特征或噪声，提高模型的泛化能力。

可视化：将高维数据集映射到低维空间（通常是二维或三维），使得数据可以用图形直观展示，便于理解和发现数据中的模式和结构。

图像处理：在图像识别和计算机视觉任务中，PCA可以用来压缩图像数据，减少计算负担，同时保持图像的主要特征不变，这对于大规模图像数据库管理和图像分类特别PCA能够去除信号中的冗余信息，提取语音的主要频谱特征，从而提高识别系统的效率和准确性。    语音识别：在语音信号处理中，PCA能够去除信号中的冗余信息，提取语音的主要频谱特征，从而提高识别系统的效率和准确性。

自然语言处理：文本数据通过PCA转换，用于提取文档的主题或语义特征，在信息检索、文本分类和情感分析等领域发挥作用。