数据结构与算法4-递归（内含LeedCode练习）

思考：

1、什么是递归？有什么优缺点？

​ 递归就像剥洋葱，将复杂问题拆分为更小、相似的子问题，并通过递归调用来解决这些子问题。

递归通常包括两个部分：基本情况（递归的终止条件）和递归情况（问题规模缩小并调用自身）。

优点是简洁、可读、问题分解。缺点是可能会增加额外的性能开销，栈溢出，因终止条件未正确设置或递归调用没有正确控制造成无限递归。

2、使用递归思想解题的思路是什么？哪些问题需要用到递归？

​ 先判断是否需要递归求解，然后推导出递推关系，以及递归的结束条件。

常用到递归的问题：求阶乘、反向打印字符串、去除链表重复元素、二分查找、杨辉三角、斐波那契数列等。

3、斐波那契数列第 n 项的求解方法有哪些？

• n 比较小时，可用递归法求解，不做任何记忆化操作，时间复杂度是 O(2^n)，存在很多冗余计算。

• 一般情况下，我们使用记忆法或者迭代的方法，实现这个转移方程，时间复杂度和空间复杂度都可以做到 O(n)。
  为了优化空间复杂度，我们可以不用保存 f(x−2) 之前的项，只用三个变量来维护 f(x−1) 和 f(x−2)，你可以理解成是把滚动数组思想应用在了动态规划中，也可以理解成是一种递推，这样把空间复杂度优化到了O(1)。

• 随着n 的不断增大 O(n) 可能已经不能满足我们的需要了，我们可以用矩阵快速幂的方法把算法加速到
  O(logn)。

• 我们也可以把 n 代入斐波那契数列的通项公式计算结果，但是如果我们用浮点数计算来实现，可能会产生精度误差。

4、如何对递归进行优化？

记忆法、滚动数组、尾调法。

5、哪些编辑器能对尾调用做优化？

C++和scala。

6、scala是什么？为什么用scala？

Scala是一种多范式编程语言，它结合了面向对象编程和函数式编程的特性。Scala运行在Java虚拟机（JVM）上，可以与Java代码无缝互操作，并且可以使用Java类库和工具。

原因：

一是多范式编程，支持面向对象和函数式编程。

二是具有可读性高、灵活性强、可扩展性好的特性，适合处理大规模、复杂性问题。

三是与Java代码无缝互操作，可以使用Java类库和工具。

Scala具有以下特点和优势：

1. 面向对象编程：Scala是一门完全面向对象的语言，支持类、对象、继承、多态等面向对象的概念和特性。它提供了强大的类和对象系统，允许开发者使用面向对象的方法组织和构建代码。
2. 函数式编程：Scala支持函数式编程范式，它提供了函数作为一等公民的特性，可以将函数作为参数传递、返回函数作为结果，以及进行高阶函数的操作。函数式编程使得代码更加简洁、可读性更高，并且能够更好地应对并发编程和异步编程的挑战。
3. 静态类型系统：Scala是一种静态类型语言，它在编译时进行类型检查，可以捕获许多常见的错误，并提供更好的代码安全性和可维护性。
4. 可扩展性：Scala具有良好的可扩展性，它支持使用特质（traits）来实现代码的复用和组合。特质类似于接口，但可以包含方法的实现。这种灵活性使得开发者可以通过组合特质来构建具有复杂行为的类和对象。
5. 并发编程：Scala通过提供并发编程的原生支持，使得开发者能够更轻松地处理并发和并行编程。它提供了Actor模型的实现，以及可变状态和共享状态的安全访问机制，从而简化了并发编程的复杂性。
6. 表达力强：Scala提供了丰富的语言特性和表达能力，代码可以更加简洁、精确，并且具有更好的可读性。它支持函数式组合、模式匹配、类型推断、集合操作等功能，使得开发者可以以更直观和优雅的方式编写代码。

7、递归的时间复杂度如何求？

当符合主定理公式可使用主定理求，不符合用展开求解。

一、 递归

1、概述

1.1定义

递归是一种解决计算问题的方法，其中解决方案取决于同一类问题的更小子集

比如单链表递归遍历的例子：

void f(Node node) {
    if(node == null) {
        return;
    }
    println("before:" + node.value)
    f(node.next);
    println("after:" + node.value)
}

说明：

1. 自己调用自己，如果说每个函数对应着一种解决方案，自己调用自己意味着解决方案是一样的（有规律的）
2. 每次调用，函数处理的数据会较上次缩减（子集），而且最后会缩减至无需继续递归
3. 内层函数调用（子集处理）完成，外层函数才能算调用完成

1.2原理

假设链表中有 3 个节点，value 分别为 1，2，3，以上代码的执行流程就类似于下面的伪码

// 1 -> 2 -> 3 -> null  f(1)

void f(Node node = 1) {
    println("before:" + node.value) // 1
    void f(Node node = 2) {
        println("before:" + node.value) // 2
        void f(Node node = 3) {
            println("before:" + node.value) // 3
            void f(Node node = null) {
                if(node == null) {
                    return;
                }
            }
            println("after:" + node.value) // 3
        }
        println("after:" + node.value) // 2
    }
    println("after:" + node.value) // 1
}

1.3解题思路

1. 确定能否使用递归求解
2. 推导出递推关系，即父问题与子问题的关系，以及递归的结束条件

例如之前遍历链表的递推关系为
$$f(n)=\{\begin{array}{ll}停止& n=null\\ f(n.next)& n\ne null\end{array}$$

• 深入到最里层叫做递
• 从最里层出来叫做归
• 在递的过程中，外层函数内的局部变量（以及方法参数）并未消失，归的时候还可以用到

2、单路递归 Single Recursion

2.1阶乘

用递归方法求阶乘

• 阶乘的定义 $n!=1\cdot 2\cdot 3\cdots (n-2)\cdot (n-1)\cdot n$，其中 $n$ 为自然数，当然 $0!=1$
• 递推关系

$$f(n)=\{\begin{array}{ll}1& n=1\\ n\ast f(n-1)& n>1\end{array}$$

代码

private static int f(int n) {
    if (n == 1) {
        return 1;
    }
    return n * f(n - 1);
}

拆解伪码如下，假设 n 初始值为 3

f(int n = 3) { // 解决不了,递
    return 3 * f(int n = 2) { // 解决不了,继续递
        return 2 * f(int n = 1) {
            if (n == 1) { // 可以解决, 开始归
                return 1;
            }
        }
    }
}

2.2反向打印字符串

用递归反向打印字符串，n 为字符在整个字符串 str 中的索引位置

• 递：n 从 0 开始，每次 n + 1，一直递到 n == str.length() - 1
• 归：从 n == str.length() 开始归，从归打印，自然是逆序的

递推关系
$$f(n)=\{\begin{array}{ll}停止& n=str.length()\\ f(n+1)& 0\le n\le str.length()-1\end{array}$$
代码为

public static void reversePrint(String str, int index) {
    if (index == str.length()) {
        return;
    }
    reversePrint(str, index + 1);
    System.out.println(str.charAt(index));
}

拆解伪码如下，假设字符串为 “abc”

void reversePrint(String str, int index = 0) {
    void reversePrint(String str, int index = 1) {
        void reversePrint(String str, int index = 2) {
            void reversePrint(String str, int index = 3) { 
                if (index == str.length()) {
                    return; // 开始归
                }
            }
            System.out.println(str.charAt(index)); // 打印 c
        }
        System.out.println(str.charAt(index)); // 打印 b
    }
    System.out.println(str.charAt(index)); // 打印 a
}

3、多路递归 Multi Recursion

3.1斐波那契数列

• 之前的例子是每个递归函数只包含一个自身的调用，这称之为 single recursion
• 如果每个递归函数例包含多个自身调用，称之为 multi recursion

递推关系
$$f(n)=\{\begin{array}{ll}0& n=0\\ 1& n=1\\ f(n-1)+f(n-2)& n>1\end{array}$$
下面的表格列出了数列的前几项

F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13
0	1	1	2	3	5	8	13	21	34	55	89	144	233

​ 每一项的值是前两个项的和，这种数列叫做斐波那契数列。

实现

public static int f(int n) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        return 1;
    }
    return f(n - 1) + f(n - 2);
}

执行流程

• 绿色代表正在执行（对应递），灰色代表执行结束（对应归）
• 递不到头，不能归，对应着深度优先搜索

时间复杂度

• 递归的次数也符合斐波那契规律，$2\ast f(n+1)-1$
• 时间复杂度推导过程
  • 斐波那契通项公式 $f(n)=\frac{1}{\sqrt{5}}\ast ({\frac{1+\sqrt{5}}{2}}^n-{\frac{1-\sqrt{5}}{2}}^n)$
  • 简化为：$f(n)=\frac{1}{2.236}\ast ({1.618}^n-{(-0.618)}^n)$
  • 带入递归次数公式 $2\ast \frac{1}{2.236}\ast ({1.618}^{n+1}-{(-0.618)}^{n+1})-1$
  • 时间复杂度为 $\Theta (1.618^n)$

1. 更多 Fibonacci 参考
2. 以上时间复杂度分析，未考虑大数相加的因素

3.2变体1 - 兔子问题

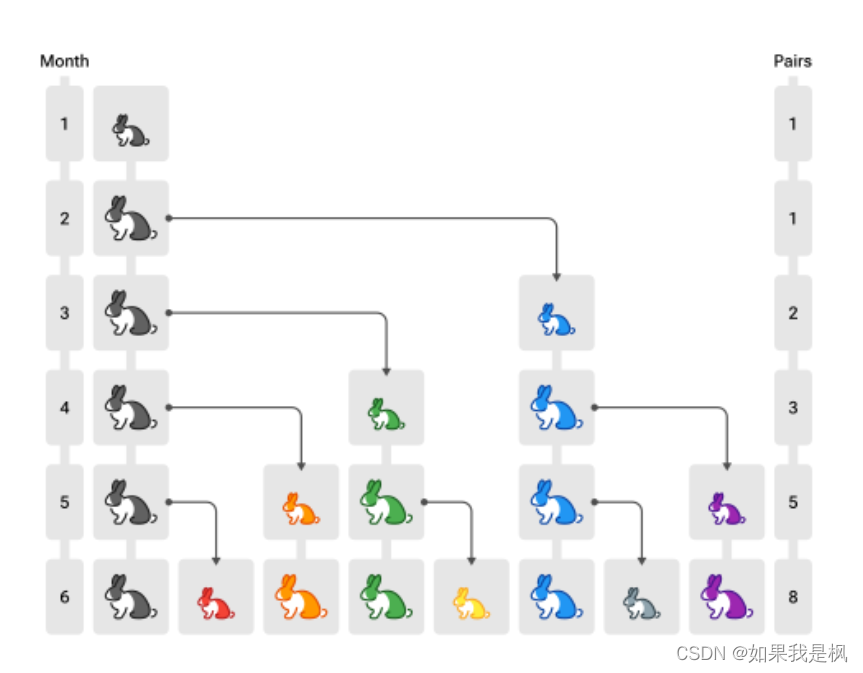
• 第一个月，有一对未成熟的兔子（黑色，注意图中个头较小）
• 第二个月，它们成熟
• 第三个月，它们能产下一对新的小兔子（蓝色）
• 所有兔子遵循相同规律，求第 $n$ 个月的兔子数

分析

兔子问题如何与斐波那契联系起来呢？设第 n 个月兔子数为 $f(n)$

• $f(n)$ = 上个月兔子数 + 新生的小兔子数
• 而【新生的小兔子数】实际就是【上个月成熟的兔子数】
• 因为需要一个月兔子就成熟，所以【上个月成熟的兔子数】也就是【上上个月的兔子数】
• 上个月兔子数，即 $f(n-1)$
• 上上个月的兔子数，即 $f(n-2)$

因此本质还是斐波那契数列，只是从其第一项开始

3.3变体2 - 青蛙爬楼梯

• 楼梯有 $n$ 阶
• 青蛙要爬到楼顶，可以一次跳一阶，也可以一次跳两阶
• 只能向上跳，问有多少种跳法

分析

n	跳法	规律
1	(1)	暂时看不出
2	(1,1) (2)	暂时看不出
3	(1,1,1) (1,2) (2,1)	暂时看不出
4	(1,1,1,1) (1,2,1) (2,1,1) (1,1,2) (2,2)	最后一跳，跳一个台阶的，基于f(3) 最后一跳，跳两个台阶的，基于f(2)
5	…	…

• 因此本质上还是斐波那契数列，只是从其第二项开始
• 对应 leetcode 题目 70. 爬楼梯 - 力扣（LeetCode）

解法一：动态规划

我们可以用「滚动数组思想」把空间复杂度优化成 O(1)

class Solution {
    public int climbStairs(int n) {
        //初始化三个变量 p、q、r，分别表示爬到第 i-2、i-1、i 级台阶的方法总数。
        int p = 0, q = 0, r = 1;
        for (int i = 1; i <= n; ++i) {
            p = q; 
            q = r; 
            //计算新的 r 值，即 p + q，表示爬到当前台阶的方法总数。
            r = p + q;
        }
        return r;
    }
}

​ 该算法的核心思想是通过保存前两个阶段的方法总数，利用迭代的方式计算当前阶段的方法总数。由于每次迭代只需要用到前两个阶段的数据，所以只需使用三个变量来保存状态，避免了使用数组来保存所有阶段的数据。这样可以减少内存消耗，并且降低了时间复杂度，使得算法更加高效。

复杂度分析

• 时间复杂度：循环执行 n 次，每次花费常数的时间代价，故渐进时间复杂度为 O(n)。
• 空间复杂度：这里只用了常数个变量作为辅助空间，故渐进空间复杂度为 O(1)。

解法二：矩阵快速幂

public class Solution {
    public int climbStairs(int n) {
        //定义了一个二维数组 q，初始值为 {{1, 1}, {1, 0}}，表示转移矩阵，其中 q[0][0] 和 q[0][1] 分别表示爬到第 i-1 和 i 级台阶的方法总数，q[1][0] 和 q[1][1] 表示爬到第 i 和 i+1 级台阶的方法总数。
        int[][] q = {{1, 1}, {1, 0}};
        //调用 pow 方法计算矩阵 q 的 n 次幂，然后返回结果矩阵 res 的第一行第一列元素的值，即爬到第 n 级台阶的方法总数。
        int[][] res = pow(q, n);
        return res[0][0];
    }
	//定义了一个方法 pow，用于计算矩阵的幂
    public int[][] pow(int[][] a, int n) {
        //初始化一个单位矩阵 ret，然后使用循环将转移矩阵 a 进行连续乘积，乘积的次数由参数 n 决定。
        int[][] ret = {{1, 0}, {0, 1}};
        while (n > 0) {
            //在每次循环中，判断 n 的最低位是否为 1，如果是，则将 ret 与 a 相乘，否则不做操作。
            if ((n & 1) == 1) {
                ret = multiply(ret, a);
            }
            //然后将 n 右移一位，将 a 与自身相乘，继续下一次循环。
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }
	//定义了一个方法 multiply，用于计算两个矩阵的乘积。
    public int[][] multiply(int[][] a, int[][] b) {
        //创建一个二维数组 c，大小为 2x2，然后使用嵌套循环遍历矩阵 a 和 b 的元素，按照矩阵乘法的规则计算出结果矩阵 c 的每个元素的值。
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
            }
        }
        return c;
    }
}

复杂度分析

• 时间复杂度：同快速幂，O*(log*n)。
• 空间复杂度：O(1)。

解法三：通项公式

public class Solution {
    public int climbStairs(int n) {
        //定义了一个变量 sqrt5，用于存储 5 的平方根。
        double sqrt5 = Math.sqrt(5);
        //使用公式 fibn = ((1 + sqrt5) / 2)^(n+1) - ((1 - sqrt5) / 2)^(n+1) 计算第 n 项斐波那契数列的值，即爬到第 n 级台阶的方法总数
        double fibn = Math.pow((1 + sqrt5) / 2, n + 1) - Math.pow((1 - sqrt5) / 2, n + 1);
        //将计算得到的结果 fibn 除以 sqrt5，然后使用 Math.round 方法进行四舍五入，得到最接近的整数结果。并将结果转换为整型并返回。

        return (int) Math.round(fibn / sqrt5);
    }
}

复杂度分析

代码中使用的 pow 函数的时空复杂度与 CPU 支持的指令集相关，这里不深入分析。可先认为时间复杂度为 O(1)。

我们来总结一下斐波那契数列第 n 项的求解方法：

• n 比较小的时候，可以直接使用过递归法求解，不做任何记忆化操作，时间复杂度是 O(2^n)，存在很多冗余计算。

• 一般情况下，我们使用「记忆化搜索」或者「迭代」的方法，实现这个转移方程，时间复杂度和空间复杂度都可以做到 O(n)。
  为了优化空间复杂度，我们可以不用保存 f(x−2) 之前的项，我们只用三个变量来维护 f(x−1) 和 f(x−2)，你可以理解成是把「滚动数组思想」应用在了动态规划中，也可以理解成是一种递推，这样把空间复杂度优化到了O(1)。

• 随着n 的不断增大 O(n) 可能已经不能满足我们的需要了，我们可以用「矩阵快速幂」的方法把算法加速到
  O(logn)。

• 我们也可以把 n 代入斐波那契数列的通项公式计算结果，但是如果我们用浮点数计算来实现，可能会产生精度误差。

4、递归优化-记忆法

上述代码存在很多重复的计算，例如求 $f(5)$ 递归分解过程

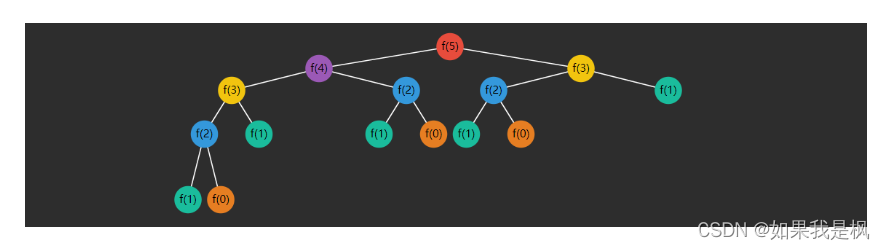
可以看到（颜色相同的是重复的）：

• $f(3)$ 重复了 2 次
• $f(2)$ 重复了 3 次
• $f(1)$ 重复了 5 次
• $f(0)$ 重复了 3 次

随着 $n$ 的增大，重复次数非常可观，如何优化呢？

Memoization 记忆法（也称备忘录）是一种优化技术，通过存储函数调用结果（通常比较昂贵），当再次出现相同的输入（子问题）时，就能实现加速效果，改进后的代码

public static void main(String[] args) {
    int n = 13;
    int[] cache = new int[n + 1];
    Arrays.fill(cache, -1);
    cache[0] = 0;
    cache[1] = 1;
    System.out.println(f(cache, n));
}


public static int f(int[] cache, int n) {
    if (cache[n] != -1) {
        return cache[n];
    }

    cache[n] = f(cache, n - 1) + f(cache, n - 2);
    return cache[n];
}

优化后的图示，只要结果被缓存，就不会执行其子问题

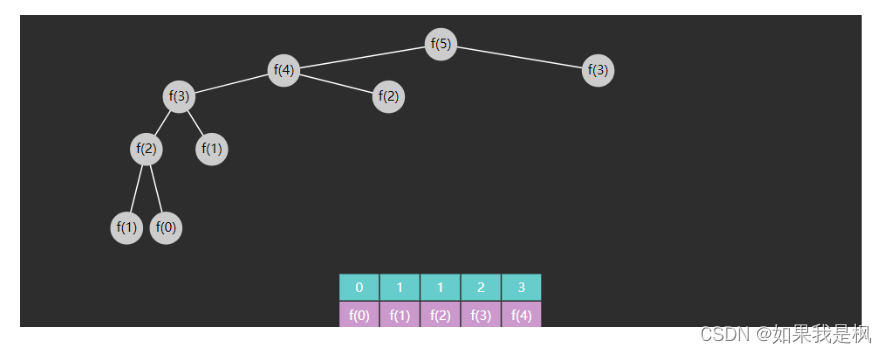
这段代码使用动态规划的思想来计算斐波那契数列的第 n 个数，并利用缓存数组 cache 记录已经计算过的中间结果，以避免重复计算。让我们逐行分析这段代码的作用：

1. 在 main 方法中，首先定义变量 n，表示要计算的斐波那契数列的第 n 个数。
2. 创建一个长度为 n + 1 的缓存数组 cache，并用 -1 初始化所有元素。
3. 将 cache[0] 设置为 0，表示斐波那契数列的第 0 个数为 0。
4. 将 cache[1] 设置为 1，表示斐波那契数列的第 1 个数为 1。
5. 调用 f 方法，并传入缓存数组 cache 和要计算的斐波那契数列的位置 n。
6. 打印计算结果。

在 f 方法中：

1. 首先，通过判断条件 if (cache[n] != -1)，如果缓存数组中已经存在斐波那契数列的第 n 个数的值，则直接返回缓存结果，避免重复计算。
2. 如果缓存数组中不存在斐波那契数列的第 n 个数的值，则通过递归调用 f 方法来计算。
3. 递归调用的参数是 cache 和 n - 1，表示计算斐波那契数列的第 n - 1 个数。
4. 同样地，递归调用的参数是 cache 和 n - 2，表示计算斐波那契数列的第 n - 2 个数。
5. 将递归调用得到的结果相加，并将结果保存到缓存数组 cache[n] 中。
6. 最后，返回缓存数组 cache[n] 的值作为计算结果。

这段代码使用动态规划的思想，通过缓存已经计算过的中间结果，避免重复计算，提高了斐波那契数列的计算效率。时间复杂度为 O(n)，其中 n 表示斐波那契数列的位置。

注意

1. 记忆法是动态规划的一种情况，强调的是自顶向下的解决
2. 记忆法的本质是空间换时间

5、递归优化-尾递归

5.1爆栈

用递归做 $n+(n-1)+(n-2)...+1$

public static long sum(long n) {
    if (n == 1) {
        return 1;
    }
    return n + sum(n - 1);
}

在我的机器上 $n=12000$ 时，爆栈了

Exception in thread "main" java.lang.StackOverflowError
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	at Test.sum(Test.java:10)
	...

为什么呢？

• 每次方法调用是需要消耗一定的栈内存的，这些内存用来存储方法参数、方法内局部变量、返回地址等等
• 方法调用占用的内存需要等到方法结束时才会释放
• 而递归调用我们之前讲过，不到最深不会回头，最内层方法没完成之前，外层方法都结束不了
  • 例如，$sum(3)$ 这个方法内有个需要执行 $3+sum(2)$，$sum(2)$ 没返回前，加号前面的 $3$ 不能释放
  • 看下面伪码

long sum(long n = 3) {
    return 3 + long sum(long n = 2) {
        return 2 + long sum(long n = 1) {
            return 1;
        }
    }
}

5.2尾调用

如果函数的最后一步是调用一个函数，那么称为尾调用，例如

function a() {
    return b()
}

下面三段代码不能叫做尾调用

function a() {
    const c = b()
    return c
}

• 因为最后一步并非调用函数

function a() {
    return b() + 1
}

• 最后一步执行的是加法

function a(x) {
    return b() + x
}

• 最后一步执行的是加法

一些语言[^11]的编译器能够对尾调用做优化，例如

function a() {
    // 做前面的事
    return b() 
}

function b() {
    // 做前面的事
    return c()
}

function c() {
    return 1000
}

a()

没优化之前的伪码

//嵌套调用
function a() {
    return function b() {
        return function c() {
            return 1000
        }
    }
}

优化后伪码如下

//平级调用
a()
b()
c()

为何尾递归才能优化？

调用 a 时

• a 返回时发现：没什么可留给 b 的，将来返回的结果 b 提供就可以了，用不着我 a 了，我的内存就可以释放

调用 b 时

• b 返回时发现：没什么可留给 c 的，将来返回的结果 c 提供就可以了，用不着我 b 了，我的内存就可以释放

如果调用 a 时

• 不是尾调用，例如 return b() + 1，那么 a 就不能提前结束，因为它还得利用 b 的结果做加法

尾递归

尾递归是尾调用的一种特例，也就是最后一步执行的是同一个函数

5.3尾递归避免爆栈

安装 Scala，安装完后直接新建项目时选Scala就行了。

Scala 入门

object Main {
  def main(args: Array[String]): Unit = {
    println("Hello Scala")
  }
}

• Scala 是 java 的近亲，java 中的类都可以拿来重用
• 类型是放在变量后面的
• Unit 表示无返回值，类似于 void
• 不需要以分号作为结尾，当然加上也对

还是先写一个会爆栈的函数

def sum(n: Long): Long = {
    if (n == 1) {
        return 1
    }
    return n + sum(n - 1)
}

• Scala 最后一行代码若作为返回值，可以省略 return

不出所料，在 $n=11000$ 时，还是出了异常

println(sum(11000))

Exception in thread "main" java.lang.StackOverflowError
	at Main$.sum(Main.scala:25)
	at Main$.sum(Main.scala:25)
	at Main$.sum(Main.scala:25)
	at Main$.sum(Main.scala:25)
	...

这是因为以上代码，还不是尾调用，要想成为尾调用，那么：

1. 最后一行代码，必须是一次函数调用
2. 内层函数必须摆脱与外层函数的关系，内层函数执行后不依赖于外层的变量或常量

def sum(n: Long): Long = {
    if (n == 1) {
        return 1
    }
    return n + sum(n - 1)  // 依赖于外层函数的 n 变量
}

如何让它执行后就摆脱对 n 的依赖呢？

• 不能等递归回来再做加法，那样就必须保留外层的 n
• 把 n 当做内层函数的一个参数传进去，这时 n 就属于内层函数了
• 传参时就完成累加, 不必等回来时累加

sum(n - 1, n + 累加器)

改写后代码如下

@tailrec
def sum(n: Long, accumulator: Long): Long = {
    if (n == 1) {
        return 1 + accumulator
    } 
    return sum(n - 1, n + accumulator)
}

• accumulator 作为累加器
• @tailrec 注解是 scala 提供的，用来检查方法是否符合尾递归
• 这回 sum(10000000, 0) 也没有问题，打印 50000005000000

执行流程如下，以伪码表示 $sum(4,0)$

// 首次调用
def sum(n = 4, accumulator = 0): Long = {
    return sum(4 - 1, 4 + accumulator)
}

// 接下来调用内层 sum, 传参时就完成了累加, 不必等回来时累加，当内层 sum 调用后，外层 sum 空间没必要保留
def sum(n = 3, accumulator = 4): Long = {
    return sum(3 - 1, 3 + accumulator)
}

// 继续调用内层 sum
def sum(n = 2, accumulator = 7): Long = {
    return sum(2 - 1, 2 + accumulator)
}

// 继续调用内层 sum, 这是最后的 sum 调用完就返回最后结果 10, 前面所有其它 sum 的空间早已释放
def sum(n = 1, accumulator = 9): Long = {
    if (1 == 1) {
        return 1 + accumulator
    }
}

本质上，尾递归优化是将函数的递归调用，变成了函数的循环调用

改循环避免爆栈

public static void main(String[] args) {
    long n = 100000000;
    long sum = 0;
    for (long i = n; i >= 1; i--) {
        sum += i;
    }
    System.out.println(sum);
}

6、递归时间复杂度-Master theorem

若有递归式
$$T(n)=aT(\frac{n}{b})+f(n)$$
其中

• $T(n)$ 是问题的运行时间，$n$ 是数据规模
• $a$ 是子问题个数
• $T(\frac{n}{b})$ 是子问题运行时间，每个子问题被拆成原问题数据规模的 $\frac{n}{b}$
• $f(n)$ 是除递归外执行的计算

令 $x={\log }_{b}a$，即 $x={\log }_{子问题缩小倍数}子问题个数$

那么
$$T(n)=\{\begin{array}{ll}\Theta (n^x)& f(n)=O(n^c)并且c<x\\ \Theta (n^x\log n)& f(n)=\Theta (n^x)\\ \Theta (n^c)& f(n)=\Omega (n^c)并且c>x\end{array}$$
例1

$T(n)=2T(\frac{n}{2})+n^4$

• 此时 $x=1<4$，由后者决定整个时间复杂度 $\Theta (n^4)$
• 如果觉得对数不好算，可以换为求【$b$ 的几次方能等于 $a$】

例2

$T(n)=T(\frac{7n}{10})+n$

• $a=1,b=\frac{10}{7},x=0,c=1$
• 此时 $x=0<1$，由后者决定整个时间复杂度 $\Theta (n)$

例3

$T(n)=16T(\frac{n}{4})+n^2$

• $a=16,b=4,x=2,c=2$
• 此时 $x=2=c$，时间复杂度 $\Theta (n^2\log n)$

例4

$T(n)=7T(\frac{n}{3})+n^2$

• $a=7,b=3,x=1.?,c=2$
• 此时 $x={\log }_{3}7<2$，由后者决定整个时间复杂度 $\Theta (n^2)$

例5

$T(n)=7T(\frac{n}{2})+n^2$

• $a=7,b=2,x=2.?,c=2$
• 此时 $x=lo{g}_{2}7>2$，由前者决定整个时间复杂度 $\Theta (n^{{\log }_{2}7})$

例6

$T(n)=2T(\frac{n}{4})+\sqrt{n}$

• $a=2,b=4,x=0.5,c=0.5$
• 此时 $x=0.5=c$，时间复杂度 $\Theta (\sqrt{n}\log n)$

例7. 二分查找递归

int f(int[] a, int target, int i, int j) {
    if (i > j) {
        return -1;
    }
    int m = (i + j) >>> 1;
    if (target < a[m]) {
        return f(a, target, i, m - 1);
    } else if (a[m] < target) {
        return f(a, target, m + 1, j);
    } else {
        return m;
    }
}

• 子问题个数 $a=1$
• 子问题数据规模缩小倍数 $b=2$
• 除递归外执行的计算是常数级 $c=0$

$T(n)=T(\frac{n}{2})+n^0$

• 此时 $x=0=c$，时间复杂度 $\Theta (\log n)$

例8. 归并排序递归

void split(B[], i, j, A[])
{
    if (j - i <= 1)                    
        return;                                
    m = (i + j) / 2;             
    
    // 递归
    split(A, i, m, B);  
    split(A, m, j, B); 
    
    // 合并
    merge(B, i, m, j, A);
}

• 子问题个数 $a=2$
• 子问题数据规模缩小倍数 $b=2$
• 除递归外，主要时间花在合并上，它可以用 $f(n)=n$ 表示

$T(n)=2T(\frac{n}{2})+n$

• 此时 $x=1=c$，时间复杂度 $\Theta (n\log n)$

例9. 快速排序递归

algorithm quicksort(A, lo, hi) is 
  if lo >= hi || lo < 0 then 
    return
  
  // 分区
  p := partition(A, lo, hi) 
  
  // 递归
  quicksort(A, lo, p - 1) 
  quicksort(A, p + 1, hi) 

• 子问题个数 $a=2$
• 子问题数据规模缩小倍数
  • 如果分区分的好，$b=2$
  • 如果分区没分好，例如分区1 的数据是 0，分区 2 的数据是 $n-1$
• 除递归外，主要时间花在分区上，它可以用 $f(n)=n$ 表示

情况1 - 分区分的好

$T(n)=2T(\frac{n}{2})+n$

• 此时 $x=1=c$，时间复杂度 $\Theta (n\log n)$

情况2 - 分区没分好

$T(n)=T(n-1)+T(1)+n$

• 此时不能用主定理求解

7、递归时间复杂度-展开求解

像下面的递归式，都不能用主定理求解

例1 - 递归求和

long sum(long n) {
    if (n == 1) {
        return 1;
    }
    return n + sum(n - 1);
}

$T(n)=T(n-1)+c$，$T(1)=c$

下面为展开过程

$T(n)=T(n-2)+c+c$

$T(n)=T(n-3)+c+c+c$

…

$T(n)=T(n-(n-1))+(n-1)c$

• 其中 $T(n-(n-1))$ 即 $T(1)$
• 带入求得 $T(n)=c+(n-1)c=nc$

时间复杂度为 $O(n)$

例2 - 递归冒泡排序

void bubble(int[] a, int high) {
    if(0 == high) {
        return;
    }
    for (int i = 0; i < high; i++) {
        if (a[i] > a[i + 1]) {
            swap(a, i, i + 1);
        }
    }
    bubble(a, high - 1);
}

$T(n)=T(n-1)+n$，$T(1)=c$

下面为展开过程

$T(n)=T(n-2)+(n-1)+n$

$T(n)=T(n-3)+(n-2)+(n-1)+n$

…

$T(n)=T(1)+2+...+n=T(1)+(n-1)\frac{2+n}{2}=c+\frac{n^2}{2}+\frac{n}{2}-1$

时间复杂度 $O(n^2)$

注：

• 等差数列求和为 $个数\ast \frac{|首项-末项|}{2}$

例3 - 递归快排

快速排序分区没分好的极端情况

$T(n)=T(n-1)+T(1)+n$，$T(1)=c$

$T(n)=T(n-1)+c+n$

下面为展开过程

$T(n)=T(n-2)+c+(n-1)+c+n$

$T(n)=T(n-3)+c+(n-2)+c+(n-1)+c+n$

…

$T(n)=T(n-(n-1))+(n-1)c+2+...+n=\frac{n^2}{2}+\frac{2cn+n}{2}-1$

时间复杂度 $O(n^2)$

不会推导的同学可以进入 https://www.wolframalpha.com/

• 例1 输入 f(n) = f(n - 1) + c, f(1) = c
• 例2 输入 f(n) = f(n - 1) + n, f(1) = c
• 例3 输入 f(n) = f(n - 1) + n + c, f(1) = c

二、练习

1、 递归 - single recursion

E03. 二分查找

​ 我们发现二分查找也可以分解成子问题，因此可以使用递归方法来解决。

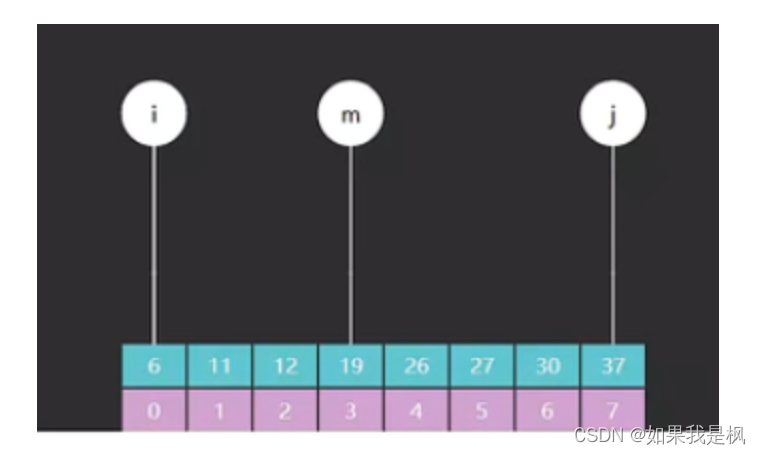
/*a -数组
  target -带查找值
  i -起始索引（包含）
  j -结束索引（包含）
*/
public static int binarySearch(int[] a, int target) {
    return recursion(a, target, 0, a.length - 1);
}

public static int recursion(int[] a, int target, int i, int j) {
    if (i > j) {
        return -1;
    }
    int m = (i + j) >>> 1;
    if (target < a[m]) {
        return recursion(a, target, i, m - 1);
    } else if (a[m] < target) {
        return recursion(a, target, m + 1, j);
    } else {
        return m;
    }
}

E04. 冒泡排序

递归冒泡排序

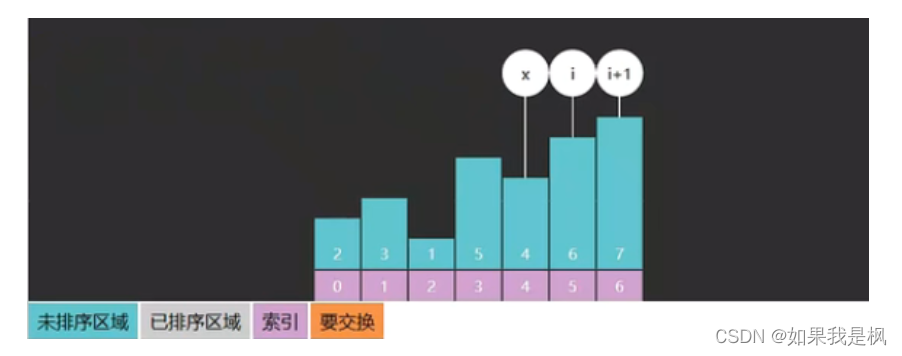
• 将数组划分成两部分[0…x] [x+1…a.length-1]
• 左边[0…x]是未排序区
• 右边[x+1…a.length-1]是已排序区
• 未排序区间内，相邻的两个元素比较，如果前一个大于后一个，则交换位置。
  

private static void bubble(int[] a, int low, int high) {
    if(low == high) {
        return;
    }
    //x 表示的是已排序与未排序的边界。
    int x = low;
    for (int i = low; i < high; i++) {
        if (a[i] > a[i + 1]) {
            swap(a, i, i + 1);
            x = i;
        }
    }
    bubble(a, low, x);
}

private static void swap(int[] a, int i, int x) {
    int t = a[i];
    a[i] = a[x];
    a[x] = t;
}


public static void main(String[] args) {
    int[] a = {3, 2, 6, 1, 5, 4, 7};
    bubble(a, 0, a.length - 1);
    System.out.println(Arrays.toString(a));
}

• low 与 high 为未排序范围

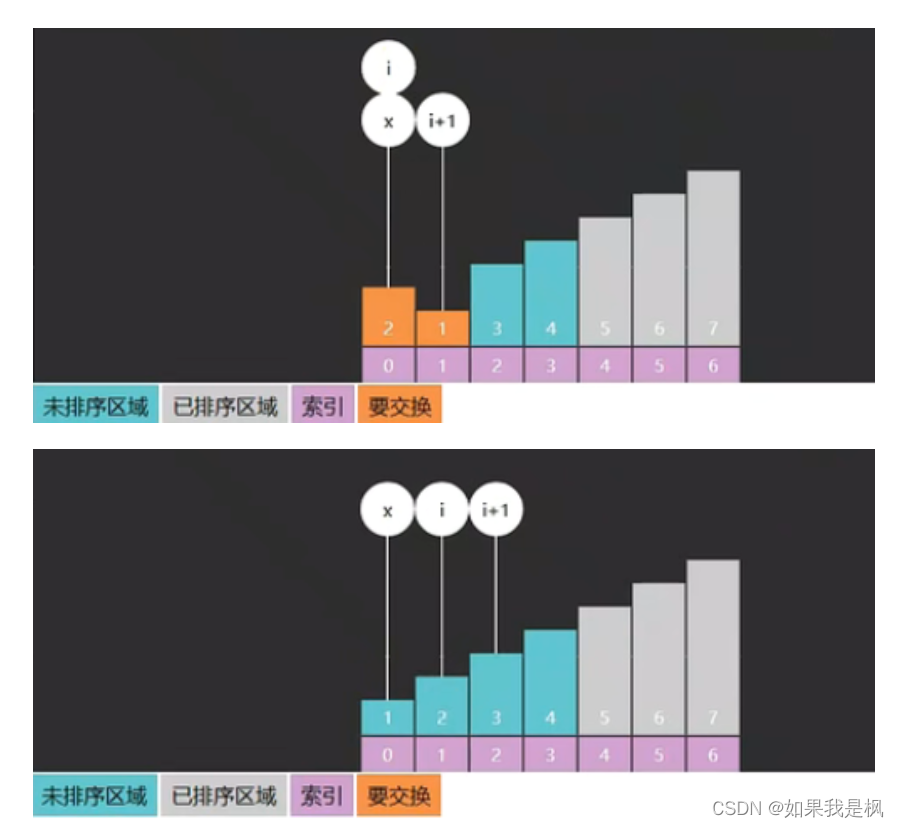
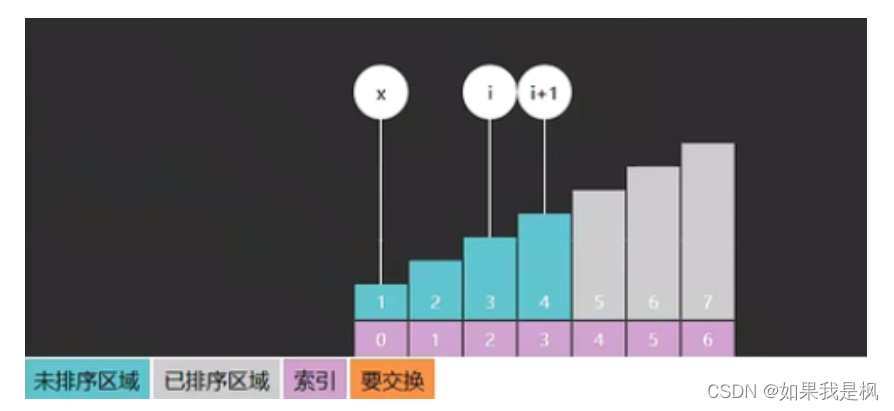
• x表示的是未排序的边界，这样X的左边就是未排序区，右边就是已排序区。

  ​ 使用x作为边界可以减少不必要的递归。如下过程，没有发生交换x一直都是0，我们只需要bubble(a, low, 0)就行了。如果不用x,我们就需要多递归几次bubble(a, low, 3)、bubble(a, low, 2)、bubble(a, low, 1)、bubble(a, low, 0)。

E05. 插入排序

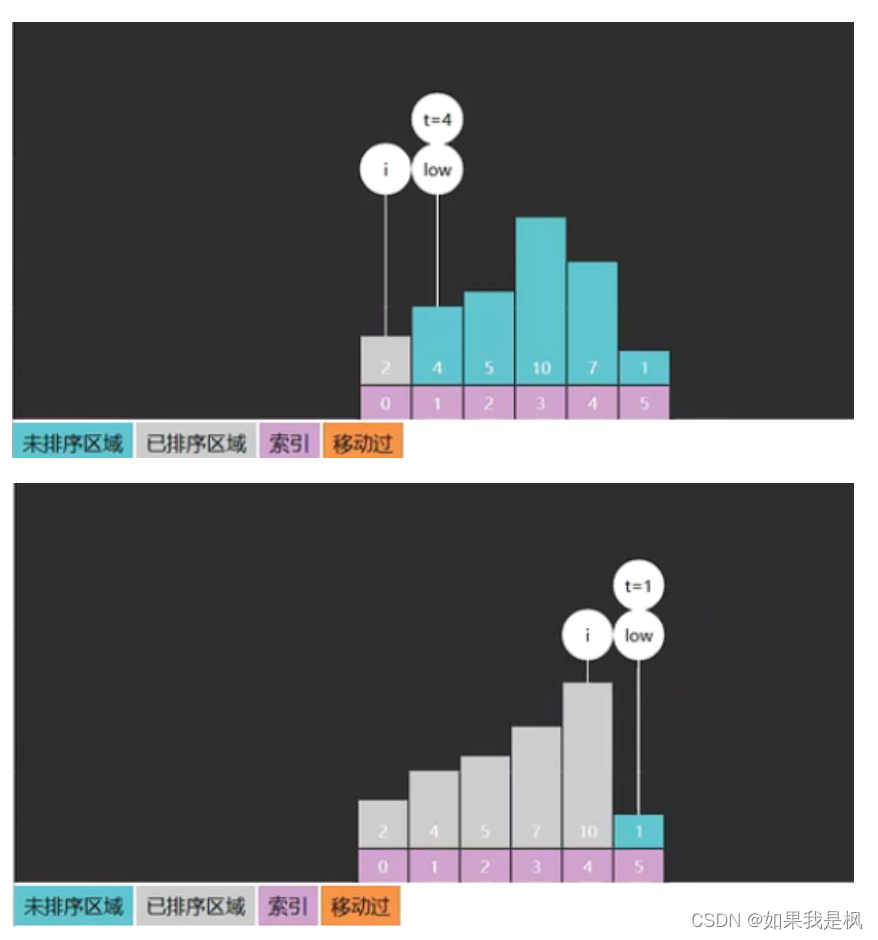
思路：通过不断将待插入元素与已排序部分的元素进行比较并移动，最终将待插入元素放置到正确的位置上。

/**
     * <h3>递归函数 将 low 位置的元素插入至 [0..low-1] 的已排序区域</h3>
     *
     * @param a   数组
     * @param low 未排序区域的左边界
     */
    private static void insertion(int[] a, int low) {
        //如果 low 等于数组长度，即遍历完成整个数组，则直接返回，结束递归
        if (low == a.length) {
            return;
        }
		//待插入元素
        int t = a[low];
        // 指向已排序区域的最后一个元素。
        int i = low - 1; 

        //找到待插入元素 t 的正确位置
        while (i >= 0 && t < a[i]) { 
            //将比待插入元素大的元素向后移动一位,空出插入位置
            a[i + 1] = a[i]; 
            //继续向前遍历比较
            i--;
        }

        // 如果 i + 1 不等于 low，进行了元素的移动，将待插入元素放置到正确位置
        if (i + 1 != low) {
            a[i + 1] = t;
        }

        //调用递归，传入数组 a 和 low + 1，继续对下一个位置的元素进行插入排序。
        insertion(a, low + 1);
    }

这段代码的时间复杂度为 O(n^2)，其中 n 是数组的长度。递归的结束条件是 low == a.length。

另一种插入排序的实现：

区别: 前者一次while循环只需赋值一次，头尾需一次。后者while循环需要赋值3次，赋值次数较多。两者时间复杂度是一样的，但是真正运行起来还是上面这个方法性能更好。

private static void insertion2(int[] a, int low) {
        if (low == a.length) {
            return;
        }

        int i = low - 1;
        while (i >= 0 && a[i] > a[i + 1]) {
            int t = a[i];
            a[i] = a[i + 1];
            a[i + 1] = t;

            i--;
        }

        insertion(a, low + 1);
    }

E06. 约瑟夫问题

$n$ 个人排成圆圈，从头开始报数，每次数到第 $m$ 个人（$m$ 从 $1$ 开始）杀之，继续从下一个人重复以上过程，求最后活下来的人是谁？

方法1

根据最后的存活者 a 倒推出它在上一轮的索引号

f(n,m)	本轮索引	为了让 a 是这个索引，上一轮应当这样排	规律
f(1,3)	0	x x x a	(0 + 3) % 2
f(2,3)	1	x x x 0 a	(1 + 3) % 3
f(3,3)	1	x x x 0 a	(1 + 3) % 4
f(4,3)	0	x x x a	(0 + 3) % 5
f(5,3)	3	x x x 0 1 2 a	(3 + 3) % 6
f(6,3)	0	x x x a

方法2

设 n 为总人数，m 为报数次数，解返回的是这些人的索引，从0开始

f(n, m)	解	规律
f(1, 3)	0
f(2, 3)	0 1 => 1	3%2=1
f(3, 3)	0 1 2 => 0 1	3%3=0
f(4, 3)	0 1 2 3 => 3 0 1	3%4=3
f(5, 3)	0 1 2 3 4 => 3 4 0 1	3%5=3
f(6, 3)	0 1 2 3 4 5 => 3 4 5 0 1	3%6=3

一. 找出等价函数

规律：下次报数的起点为 $k=m\%n$

• 首次出列人的序号是 $k-1$，剩下的的 $n-1$ 个人重新组成约瑟夫环
• 下次从 $k$ 开始数，序号如下
  • $k,k+1,...,0,1,k-2$，如上例中 $34501$

这个函数称之为 $g(n-1,m)$，它的最终结果与 $f(n,m)$ 是相同的。

二. 找到映射函数

现在想办法找到 $g(n-1,m)$ 与 $f(n-1,m)$ 的对应关系，即
$$\begin{gathered} 3\to 0 \\ 4\to 1 \\ 5\to 2 \\ 0\to 3 \\ 1\to 4 \end{gathered}$$
映射函数为
$$mapping(x)=\{\begin{array}{ll}x-k& x=[k..n-1]\\ x+n-k& x=[\mathrm{0..}k-2]\end{array}$$
等价于下面函数
$$mapping(x)=(x+n-k)\%n$$
代入测试一下
$$\begin{gathered} 3\to (3+6-3)\%6\to 0 \\ 4\to (4+6-3)\%6\to 1 \\ 5\to (5+6-3)\%6\to 2 \\ 0\to (0+6-3)\%6\to 3 \\ 1\to (1+6-3)\%6\to 4 \end{gathered}$$
综上有
$$f(n-1,m)=mapping(g(n-1,m))$$
三. 求逆映射函数

映射函数是根据 x 计算 y，逆映射函数即根据 y 得到 x
$$mappin{g}^{-1}(x)=(x+k)\%n$$
代入测试一下
$$\begin{gathered} 0\to (0+3)\%6\to 3 \\ 1\to (1+3)\%6\to 4 \\ 2\to (2+3)\%6\to 5 \\ 3\to (3+3)\%6\to 0 \\ 4\to (4+3)\%6\to 1 \end{gathered}$$
因此可以求得
$$g(n-1,m)=mappin{g}^{-1}(f(n-1,m))$$
四. 递推式

代入推导
$$\begin{array}{rl}f(n,m)=& g(n-1,m)\\ =& mappin{g}^{-1}(f(n-1,m))\\ =& (f(n-1,m)+k)\%n\\ =& (f(n-1,m)+m\%n)\%n\\ =& (f(n-1,m)+m)\%n\end{array}$$
最后一步化简是利用了模运算法则

$(a+b)\%n=(a\%n+b\%n)\%n$ 例如

• $(6+6)\%5=2=(6+6\%5)\%5$
• $(6+5)\%5=1=(6+5\%5)\%5$
• $(6+4)\%5=0=(6+4\%5)\%5$

最终递推式
$$f(n,m)=\{\begin{array}{ll}(f(n-1,m)+m)\%n& n>1\\ 0& n=1\end{array}$$

2、 递归 - multi recursion

E02. 汉诺塔

Tower of Hanoi，是一个源于印度古老传说：大梵天创建世界时做了三根金刚石柱，在一根柱子从下往上按大小顺序摞着 64 片黄金圆盘，大梵天命令婆罗门把圆盘重新摆放在另一根柱子上，并且规定

• 一次只能移动一个圆盘
• 小圆盘上不能放大圆盘

下面的动图演示了4片圆盘的移动方法

使用程序代码模拟圆盘的移动过程，并估算出时间复杂度

思路

• 假设每根柱子标号 a，b，c，每个圆盘用 1，2，3 … 表示其大小，圆盘初始在 a，要移动到的目标是 c

• 如果只有一个圆盘，此时是最小问题，可以直接求解

  • 移动圆盘1 $a\mapsto c$

• 如果有两个圆盘，那么

  • 圆盘1 $a\mapsto b$
  • 圆盘2 $a\mapsto c$
  • 圆盘1 $b\mapsto c$

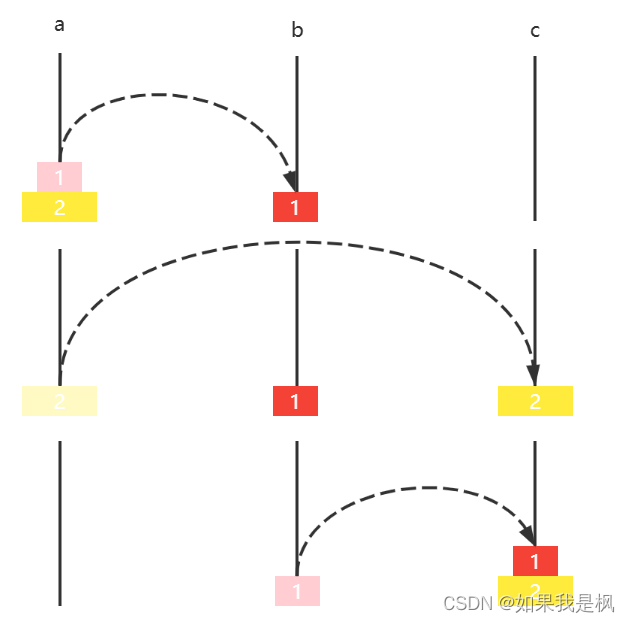
• 如果有三个圆盘，那么

  • 圆盘12 $a\mapsto b$
  • 圆盘3 $a\mapsto c$
  • 圆盘12 $b\mapsto c$

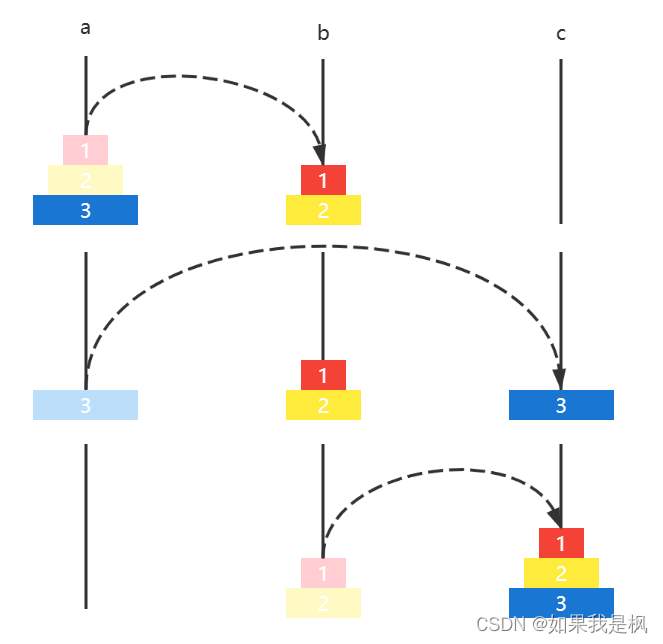
• 如果有四个圆盘，那么

  • 圆盘 123 $a\mapsto b$
  • 圆盘4 $a\mapsto c$
  • 圆盘 123 $b\mapsto c$

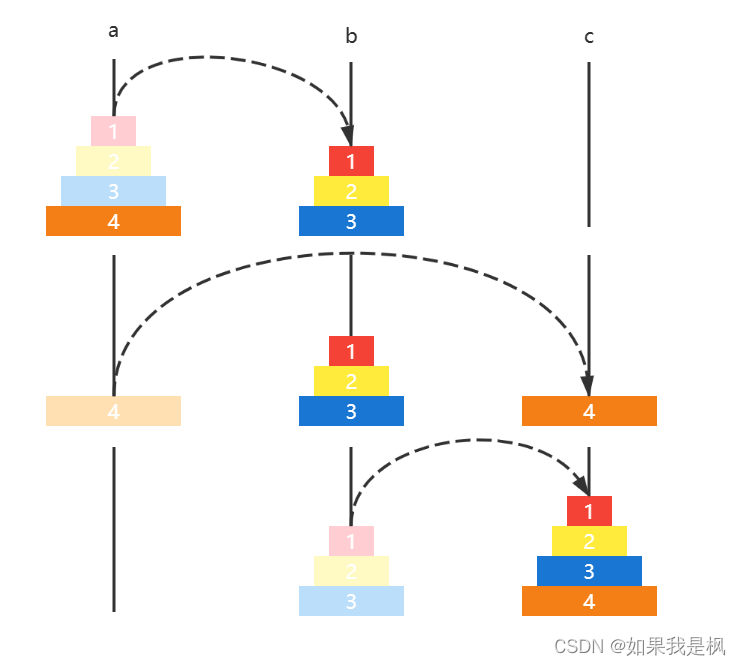
题解

/**
 * 递归汉诺塔
 */
public class E02HanoiTower {
    static LinkedList<Integer> a = new LinkedList<>();
    static LinkedList<Integer> b = new LinkedList<>();
    static LinkedList<Integer> c = new LinkedList<>();

    static void init(int n) {
        for (int i = n; i >= 1; i--) {
            a.addLast(i);
        }
    }
/**
     * <h3>移动圆盘</h3>
     *
     * @param n 圆盘个数
     * @param a 原
     * @param b 借
     * @param c 目
     */
    static void move(int n, LinkedList<Integer> a,
                     LinkedList<Integer> b,
                     LinkedList<Integer> c) {
        if (n == 0) {
            return;
        }
        move(n - 1, a, c, b);   // 把 n-1 个盘子由a,借c,移至b
        c.addLast(a.removeLast()); // 把最后的盘子由 a 移至 c
//        print();
        move(n - 1, b, a, c);   // 把 n-1 个盘子由b,借a,移至c
    }

    // T(n) = 2T(n-1) + c,  O(2^64)


    public static void main(String[] args) {
        //创建了一个 StopWatch 对象 sw，用于计时
        StopWatch sw = new StopWatch();
        int n = 1;
        init(n);
        print();
        //启动计时器，标记计时开始。
        sw.start("n=1");
        move(n, a, b, c);
        // 停止计时器
        sw.stop();
        print();
        //打印计时器的结果，即运行时间
        System.out.println(sw.prettyPrint());
    }

    private static void print() {
        System.out.println("----------------");
        System.out.println(a);
        System.out.println(b);
        System.out.println(c);
    }

让我们逐行分析这段代码的作用：

1. 首先，在类 E02HanoiTower 中定义了三个静态变量 a、b 和 c，分别表示三个塔座。这里使用了 LinkedList 来表示塔座，其中存储了盘子的大小，越靠前的元素表示越大的盘子。
2. init 方法用于初始化塔座 a，将 n 个盘子按照从大到小的顺序放置在塔座 a 上。
3. h 方法是递归解决汉诺塔问题的核心方法。它接受参数 n 表示要移动的盘子数量，a、b、c 表示三个塔座。在方法中，首先判断递归终止条件 if (n == 0)，如果没有盘子需要移动，则直接返回。
4. 接下来，通过递归调用 h 方法，将 n-1 个盘子从塔座 a 移动到塔座 b，并且使用塔座 c 作为辅助塔座。
5. 将最后一个盘子从塔座 a 移动到塔座 c。
6. 调用 print 方法，打印当前塔座的状态。
7. 再次通过递归调用 h 方法，将之前移动到塔座 b 上的 n-1 个盘子从塔座 b 移动到塔座 c，并且使用塔座 a 作为辅助塔座。
8. print 方法用于打印当前三个塔座的状态。
9. 在 main 方法中，首先调用 init 方法初始化塔座 a，并且打印初始状态。
10. 调用 h 方法，将 n=3 个盘子从塔座 a 移动到塔座 c，并且使用塔座 b 作为辅助塔座。
11. 最后再次调用 print 方法，打印最终状态。

该代码通过递归的方式实现了汉诺塔问题的解决方案，每次移动时通过递归调用将 n-1 个盘子从一个塔座。

时间复杂度：O(2^n)

E03. 杨辉三角

分析

把它斜着看

1
1   1
1   2   1
1   3   3   1
1   4   6   4   1

• 行 $i$，列 $j$，那么 $[i][j]$ 的取值应为 $[i-1][j-1]+[i-1][j]$
• 当 $j=0$ 或 $i=j$ 时，$[i][j]$ 取值为 $1$

题解

/**
 * 递归杨辉三角(Pascal三角)
 */
public class E03PascalTriangle {

    /**
     * <h3>直接递归(未优化)</h3>
     *
     * @param i 行坐标
     * @param j 列坐标
     * @return 该坐标元素值
     */
    private static int element(int i, int j) {
        if (j == 0 || i == j) {
            return 1;
        }
        return element(i - 1, j - 1) + element(i - 1, j);
    }

    private static void printSpace(int n, int i) {
        int num = (n - 1 - i) * 2;
        for (int j = 0; j < num; j++) {
            System.out.print(" ");
        }
    }

    public static void print(int n) {
        for (int i = 0; i < n; i++) {
//            printSpace(n, i);
            for (int j = 0; j <= i; j++) {
                System.out.printf("%-4d", element(i, j));
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
//        System.out.println(element(4, 2));
        print2(6);
    }

    /*
        1
        1   1
        1   2   1
        1   3   3   1
        1   4   6   4   1
        1   5   10  10  5   1
     */

优化1

是 multiple recursion，因此很多递归调用是重复的，例如

• recursion(3, 1) 分解为
  • recursion(2, 0) + recursion(2, 1)
• 而 recursion(3, 2) 分解为
  • recursion(2, 1) + recursion(2, 2)

这里 recursion(2, 1) 就重复调用了，事实上它会重复很多次，可以用 static AtomicInteger counter = new AtomicInteger(0) 来查看递归函数的调用总次数

事实上，可以用 memoization 来进行优化：

 /**
     * <h3>优化1 - 使用二维数组记忆法</h3>
     *
     * @param triangle 二维数组
     * @param i        行坐标
     * @param j        列坐标
     * @return 该坐标元素值
     */
    private static int element1(int[][] triangle, int i, int j) {
        if (triangle[i][j] > 0) {
            return triangle[i][j];
        }

        if (j == 0 || i == j) {
            triangle[i][j] = 1;
            return 1;
        }
        triangle[i][j] = element1(triangle, i - 1, j - 1) + element1(triangle, i - 1, j);
        return triangle[i][j];
    }

    public static void print1(int n) {
        int[][] triangle = new int[n][];
        for (int i = 0; i < n; i++) { // 行
            triangle[i] = new int[i + 1];
//            printSpace(n, i);
            for (int j = 0; j <= i; j++) {
                System.out.printf("%-4d", element1(triangle, i, j));
            }
            System.out.println();
        }
    }

• 将数组作为递归函数内可以访问的遍历，如果 $triangle[i][j]$ 已经有值，说明该元素已经被之前的递归函数计算过，就不必重复计算了

二维数组优点是时间上快了，但是空间上有额外的占用。

​ 那么在空间上我们可以再优化吗？当然，我们可以通过滚动数组的方式节约空间，新的值覆盖旧的值。

优化2

/**
     * <h3>优化2 - 使用一维数组记忆法</h3>
     */
    /*
        0   0   0   0   0   0   初始状态
        1   0   0   0   0   0   i=0
        1   1   0   0   0   0   i=1
        1   2   1   0   0   0   i=2
        1   3   3   1   0   0   i=3
        1   4   6   4   1   0   i=4 *
     */
    private static void createRow(int[] row, int i) {
        //第一行，直接将 row 数组的第一个元素设为 1
        if (i == 0) {
            row[0] = 1;
            return;
        }
        //从当前行数 i 开始，递减到 1，每次迭代都将 row[j] 的值更新为 row[j] + row[j - 1]，即当前位置的值加上前一位置的值。
        for (int j = i; j > 0; j--) {
            row[j] = row[j] + row[j - 1];
        }
    }

    public static void print2(int n) {
        //创建一个长度为 n 的整数数组 row，用于存储每一行的数据。
        int[] row = new int[n];
        for (int i = 0; i < n; i++) { // 行
            createRow(row, i);
//            printSpace(n, i);
            for (int j = 0; j <= i; j++) {
                System.out.printf("%-4d", row[j]);
            }
            System.out.println();
        }
    }

注意：还可以通过每一行的前一项计算出下一项，不必借助上一行，这与杨辉三角的另一个特性有关，暂不展开了

Ex杨辉三角118题

118. 杨辉三角 - 力扣（LeetCode）

给定一个非负整数 *numRows，*生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

class Solution {
    public List<List<Integer>> generate(int numRows) {
        //创建一个 ret 变量，类型为 List<List<Integer>>，用于存储生成的杨辉三角
        List<List<Integer>> ret = new ArrayList<List<Integer>>();
        for (int i = 0; i < numRows; ++i) {
            //在每一行开始时，创建一个空的 row 列表，用于存储当前行的数字
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                //判断当前位置是否在行的开头或结尾（即 j 是否等于 0 或 i），如果是，则将数字 1 添加到 row 列表中。
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    //如果当前位置不在行的开头或结尾，根据杨辉三角的规律，将上一行中同一列和前一列的数字相加，并将结果添加到 row 列表中。
                    row.add(ret.get(i - 1).get(j - 1) + ret.get(i - 1).get(j));
                }
            }
            //将 row 列表添加到 ret 列表中，表示生成的杨辉三角的当前行。
            ret.add(row);
        }
        return ret;
    }
}

Ex杨辉三角119题

119. 杨辉三角 II - 力扣（LeetCode）

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

方法一：递推

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<List<Integer>> C = new ArrayList<List<Integer>>();
        for (int i = 0; i <= rowIndex; ++i) {
            List<Integer> row = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    row.add(1);
                } else {
                    row.add(C.get(i - 1).get(j - 1) + C.get(i - 1).get(j));
                }
            }
            C.add(row);
        }
        return C.get(rowIndex);
    }
}

优化

注意到对第 i+1 行的计算仅用到了第 i 行的数据，因此可以使用滚动数组的思想优化空间复杂度。

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> pre = new ArrayList<Integer>();
        for (int i = 0; i <= rowIndex; ++i) {
            List<Integer> cur = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    cur.add(1);
                } else {
                    cur.add(pre.get(j - 1) + pre.get(j));
                }
            }
            pre = cur;
        }
        return pre;
    }
}

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add(0);
            for (int j = i; j > 0; --j) {
                row.set(j, row.get(j) + row.get(j - 1));
            }
        }
        return row;
    }
}

方法二：线性递推

class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        //在每次循环中，计算当前位置的值。根据杨辉三角的性质，第 i 个位置的值等于前一个位置的值乘以 (rowIndex - i + 1) / i。
        for (int i = 1; i <= rowIndex; ++i) {
            //注意，为了避免整数除法产生的精度问题，将 (long) 强制类型转换应用于 row.get(i - 1)，并将结果转回 int 类型。
            row.add((int) ((long) row.get(i - 1) * (rowIndex - i + 1) / i));
        }
        //列表 row 中存储了杨辉三角的第 rowIndex+1 行数据。
        return row;
    }
}