一、脉冲压缩原理
1.1 进行脉冲压缩的原因
由雷达测距公式:R=1/2*c*t 可以得到,
雷达分辨率:ρ=1/2*c*Tp,频域上:ρ'=1/2*c*1/B。
其中,c为光速、Tp为脉冲持续时间、B为发射信号带宽。

发现在Tp减小、B增大的情况下,ρ减小,即雷达分辨率增强。但由雷达方程可知,Tp减小会导致雷达可以测量到的最大距离变小。这就出现了鱼与熊掌不可兼得的问题。
脉冲压缩技术就是为了解决这一问题,在增强分辨率的同时,保证测距能力。
1.2 脉冲压缩的条件
要求Tp*B>1。
1.3 具体实现方法。
构建匹配滤波器,在匹配滤波中,滤波器的时域响应需要是发射信号的时间反转再取复共轭。
例如,回波信号为:S(t),匹配滤波器为:h(t)=S*(-t)。
将回波信号S(t)与h(t)求卷积,得出滤波器的输出信号,即为压缩后的信号。
也可以将S(t)和h(t)都经过傅里叶变换到频域上,相乘之后再逆傅里叶变化得到脉压信号。
二、实验要求
我们复现一下南航《雷达成像技术》教学视频中,毛新华教授讲授的例题:

三、代码实现
分别给出两套代码,实现效果相同。
实现过程中,3.1用的是将S(t)和h(t)都经过傅里叶变换到频域上,相乘之后再逆傅里叶变化得到脉压信号。3.2则是将回波信号S(t)与h(t)求卷积,得出脉压信号。
3.1 视频中代码
c = 3e8; % 光速 (m/s)
Tp = 2e-6; % 脉冲宽度 (s)
Br = 100e6; % 带宽 (Hz)
kr = Br / Tp; % 调频率 (Hz/s)
fs = 120e6; % 采样频率 (Hz)
r1 = 10e3; % 目标1的距离 (m)
r2 = 10e3 + 100; % 目标2的距离 (m)
r3 = 10e3 + 500; % 目标3的距离 (m)
Tu = 20e-6; % 时间窗口 (s)
N = round(Tu * fs); % 采样点数
t = 2 * r1 / c + linspace(-Tu/2, Tu/2, N); % 时间轴,为方便观察,以第一个回波为观察中心。
t1 = 2 * r1 / c; % 第一个目标回波接收时间
t2 = 2 * r2 / c; % 第二个目标回波接收时间
t3 = 2 * r3 / c; % 第三个目标回波接收时间
rt = exp(1j * pi * kr * (t - t1).^2) .* (abs(t - t1) < Tp/2);
rt = rt + exp(1j * pi * kr * (t - t2).^2) .* (abs(t - t2) < Tp/2);
rt = rt + exp(1j * pi * kr * (t - t3).^2) .* (abs(t - t3) < Tp/2); % 得到回波信号表达式
figure(1)
plot(t, real(rt)) % 观察回波信号实部
f = linspace(-fs/2, fs/2, N); % 频率轴
Hf = (abs(f) < Br/2) .* exp(1j * pi * f.^2 / kr); % 匹配滤波器
Hf = fftshift(Hf); % 将频率轴中心化
rt = ifft(fft(rt) .* Hf); % 频域匹配滤波
figure(2)
plot(t, abs(rt)) % 观察脉冲压缩后回波幅度值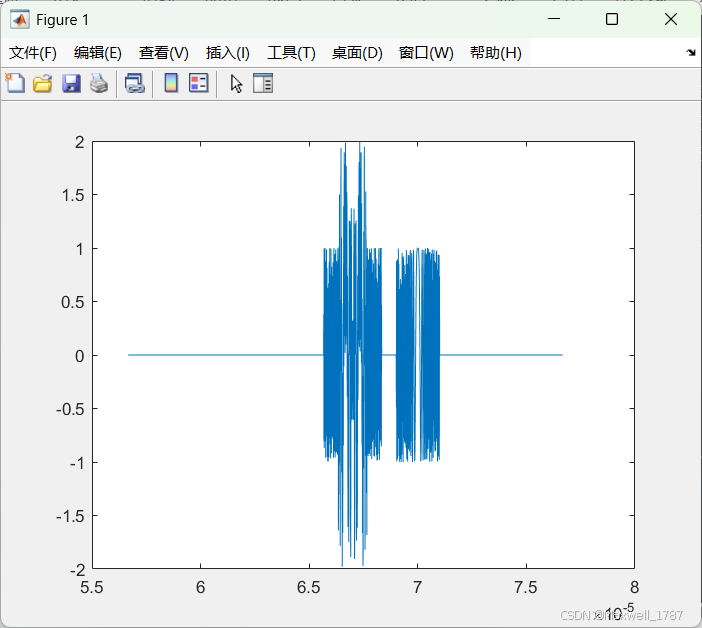

3.2 同效果代码
% 雷达脉冲压缩仿真实验
clear; clc; close all;
%% 参数设置
c = 3e8; % 光速 (m/s)
tau = 2e-6; % 脉冲宽度 (s)
B = 100e6; % 带宽 (Hz)
Fs = 120e6; % 采样频率 (Hz)
targets = [10e3, 10.1e3, 10.5e3]; % 目标距离 (m)
%% 生成线性调频信号 (LFM)
t_chirp = 0:1/Fs:tau-1/Fs; % 发射信号时间轴
mu = B / tau; % 调频率 (Hz/s)
s_tx = exp(1j * pi * mu * t_chirp.^2); % 发射信号(复基带)
%% 计算目标时延对应的采样点
delay_time = 2 * targets / c; % 往返时延 (s)
delay_samples = round(delay_time * Fs); % 采样点索引
%% 生成回波信号(叠加三个目标)
max_idx = max(delay_samples) + length(s_tx); % 最大索引
echo_signal = zeros(1, max_idx); % 初始化回波信号
% 将发射信号复制到对应时延位置
for i = 1:length(targets)
start_idx = delay_samples(i) + 1;
end_idx = start_idx + length(s_tx) - 1;
echo_signal(start_idx:end_idx) = echo_signal(start_idx:end_idx) + s_tx;
end
%% 脉冲压缩处理(匹配滤波)
matched_filter = conj(fliplr(s_tx)); % 匹配滤波器是发射信号的共轭反转
compressed_signal = conv(echo_signal, matched_filter, 'same'); %卷积
%% 结果可视化
% 时间轴生成(单位:微秒)
t_tx_plot = t_chirp * 1e6;
t_echo_plot = (0:length(echo_signal)-1) / Fs * 1e6;
t_compressed_plot = (0:length(compressed_signal)-1) / Fs * 1e6;
figure('Position', [100, 100, 800, 600])
% 发射信号(实部/虚部)
subplot(3,1,1)
plot(t_tx_plot, real(s_tx), 'b', t_tx_plot, imag(s_tx), 'r')
title('发射信号(实部与虚部)')
xlabel('时间 (\mus)'), ylabel('幅度')
legend('实部', '虚部')
xlim([0, tau*1e6])
% 回波信号(幅度)
subplot(3,1,2)
plot(t_echo_plot, abs(echo_signal))
title('回波信号(幅度)')
xlabel('时间 (\mus)'), ylabel('幅度')
xlim([0, max(t_echo_plot)])
% 脉冲压缩结果(幅度)
subplot(3,1,3)
plot(t_compressed_plot, abs(compressed_signal))
title('脉冲压缩结果(幅度)')
xlabel('时间 (\mus)'), ylabel('幅度')
xlim([0, max(t_compressed_plot)])
%% 显示目标峰值位置
[~, peaks] = findpeaks(abs(compressed_signal), 'MinPeakHeight', max(abs(compressed_signal))/2);
peak_times = t_compressed_plot(peaks);
disp('目标检测结果:');
fprintf('理论时延 (μs) | 实际时延 (μs)\n');
fprintf('------------------------------\n');
for i = 1:length(targets)
fprintf('%9.2f | %9.2f\n', delay_time(i)*1e6, peak_times(i));
end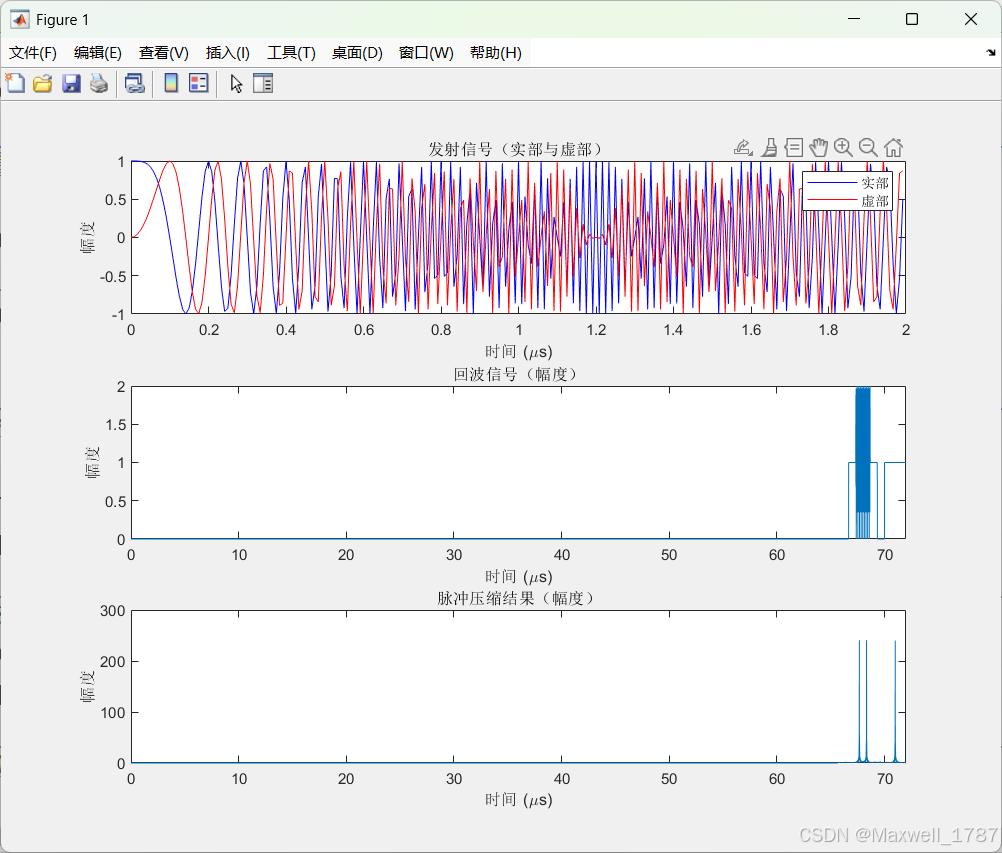























 7798
7798

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








